考虑直流偏移影响的电网阻抗识别方法

李 晋，安 婷

(国网甘肃省电力公司庆阳供电公司，甘肃 庆阳 745000)

0 引言

随着风力和光伏等可再生能源发电技术的发展，越来越多的并网转换器连接到了电网[1-3]。并网转换器的大量接入导致电网的阻抗特性发生了显著变化，这将会影响这些并网转换器的稳定性[4-5]，进而威胁电网安全运行。为了提高这些并网转换器的运行稳定性，有必要在线识别电网阻抗，然后相应地调整这些并网转换器的控制模式。

文中提出了一种考虑直流偏移的复示数滤波器(complex coefficient filtering，CCF)电 网阻抗的检测方法。通过在常规CCF的前向通道上增加一个高通滤波器s/(s+ω1)，改进CCF结构，消除了直流偏移的影响，从而提高了电网阻抗识别的精度。

1 并网转换器并网点阻抗辨识系统

如图1，基于公共耦合点(point of common coupling，PCC)处电压的电角度，对转换器的输出电流进行采样并转换在同步旋转坐标系下。然后，使用比例积分(PI)控制器来控制电流。在计算之后，获得参考电压uαref，uβref。通常，通过与三角波进行载波比较的方式生成PWM信号。为了识别电网阻抗，在调制波里注入高频信号，通过PWM输出，使逆变器输出的电压电流中含有高频非特性谐波信号，从而实现向PCC点注入高频信号，即将高频非特性谐波电压uαh，uβh分别叠加到参考电压uαref，uβref上，得到uiref和uih之和(i=α，β)，再进行载波比较生成PWM，然后通过数字信号滤波器提取PCC处的高频电压和电流，通过计算得出电网阻抗。

注入的高频非特性谐波电压uαh，uβh表示为：

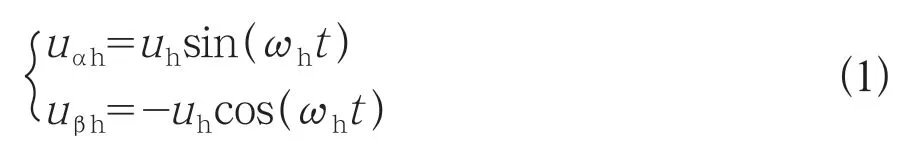
其中，uh表示注入的高频非特性谐波电压的幅度；ωh表示注入的电压的角频率。

2 CCF并网点阻抗辨识方法

2.1 常规CCF并网点阻抗辨识方法

常规CCF并网点阻抗辨识方法将高频非特征谐波电压注入PCC之后，根据在PCC处采样电压和电流提取高频电压和电流。其控制框见图1，ugαβ，igαβ表示采样得到的PCC点电压和电流，满足：ugαβ=[ugβ，ugβ]T，igαβ=[igβ，igβ]T，s表 示 拉 普拉斯算子，ωhc，ωc表示截止频率，ω0表示电网频率。

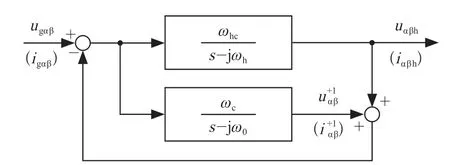
图1 常规方法下复系数滤波器

如果CCF的输入信号是PCC处的采样电压，则输出信号是其在注入频率下的高频分量。为显示CCF的滤波特性，采用波特图进行分析，ωh设置为3 297 rad/s，ωc设置为221 rad/s，角频率ω0为314 rad/s。ωhc分 别 设 置 为800 rad/s，300 rad/s和100 rad/s，测试其对滤波器特性的影响，其滤波特性如图2所示。

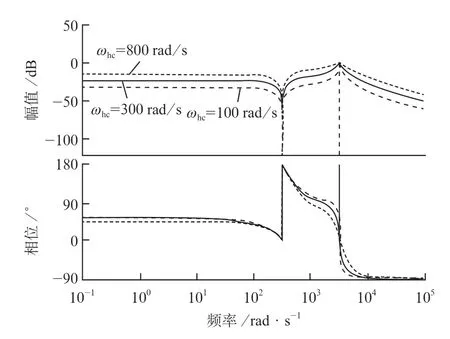
图2 复系数滤波器波特

从图2可知，较小的ωhc可以增强CCF的谐波抑制能力，但当ωhc太小时，动态响应速度就会降低[6]。因此，选择ωhc为300 rad/s。通过图2和CCF的传递函数G1(式2)可以看出，采用传统的CCF控制方法，直流偏移的影响无法完全消除。

其中a和b表示为：

由于在实际的控制系统中，采样电路采样得到的电压、电流等信号都会含有直流偏移，而传统CCF无法完全消除直流偏移的影响。因此，为了进一步提高电网阻抗检测精度，应该进一步改进以完全消除直流偏移的影响。

2.2 考虑直流偏移的CCF并网点阻抗辨识方法

为了消除直流偏移的影响，提出了一种考虑直流偏移影响的CCF，如图3所示。

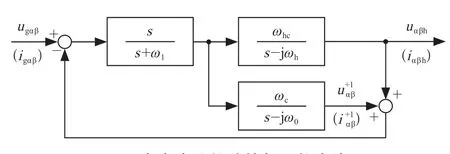
图3 考虑直流偏移的复系数滤波器

在CCF的前向通道上增加一个高通滤波器。其传递函数如式(5)：

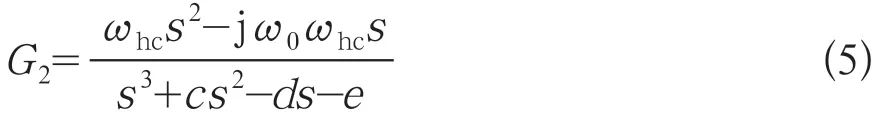
其中c，d和e表示为：

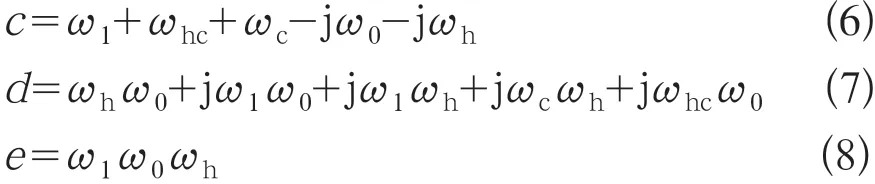
从式(5)可以看出，当s=0时，G2=0，这意味着CCF对0频信号，即对直流信号可以实现完全的抑制消除，提高高频信号的提取精度。为了进一步显示其滤波特性，其滤波特性如图4所示，其中ωh设置为300 rad/s。

从图4中可知，截止频率ω1不影响其高频滤波特性。当ω1减小时，CCF的低频抑制能力降低，而当ω1增大时，动态响应速度将降低。因此，为简化起见，设ω1=ω0。

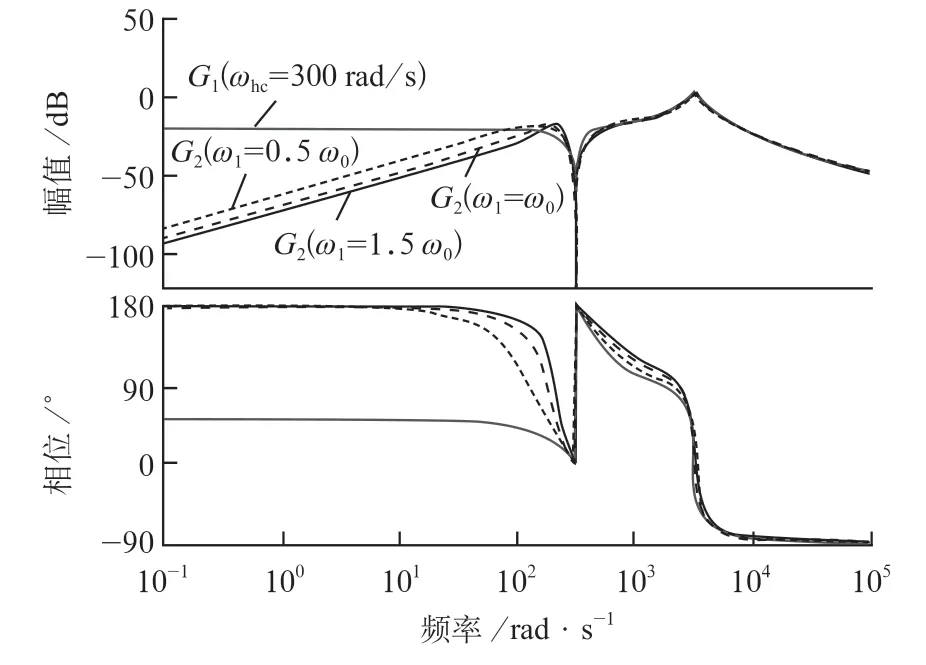
图4 考虑直流偏移复系数滤波器波特

由于图4所示复系数滤波器结构含有虚数j，因此无法直接实现。为此，结合文献[7]和式(9)设计考虑直流偏移的CCF实现框如图5所示，消除直流偏移的影响，准确提取高频电压和电流，其中输入端为ugi时输出为uih，输入端为igi时输出为iih(i=α，β)。

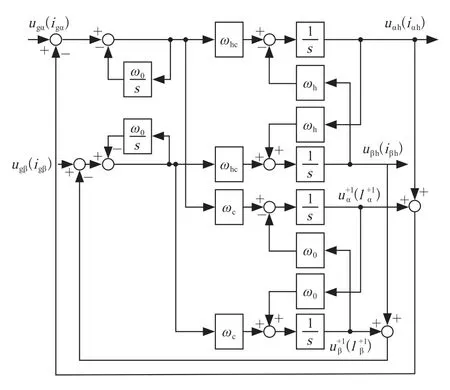
图5 考虑直流偏移的CCF实现框

然后，基于式(10)计算电网阻抗。

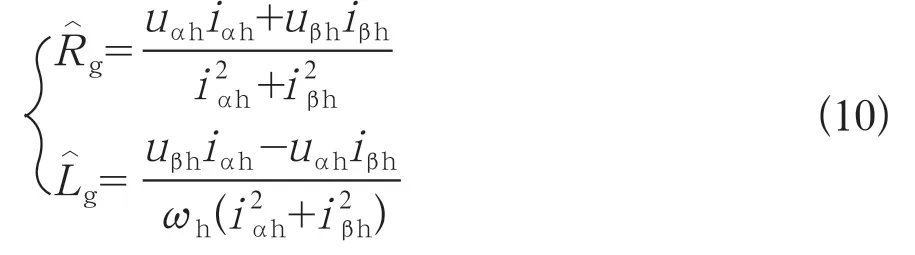
其中，uαh，uβh是CCF提取的高频电压;iαh，iβh是CCF提取的高频电流;是计算电网电阻是计算的电网电感。

3 仿真结果及分析

为验证所提出的电网阻抗检测方法的可行性和有效性，基于MATLAB/Simulink进行了仿真研究。控制框如图6所示，包括直流偏置抑制模块、基波信号提取模块和高频信号提取模块。仿真中使用的参数如下：udc=700 V，L1=5 mH，C=15.6 μF，Rd=2 Ω，Rg=1 Ω，Lg在0.4 s时 从1.2 mH升至2.4 mH，0.8 s时降至1.2 mH。

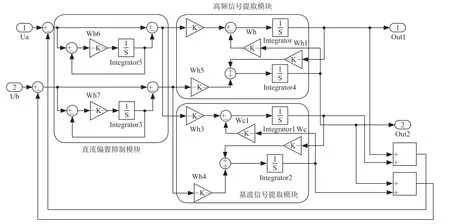
图6 考虑采样直流偏移的CCF仿真模型

为验证所提方法的有效性，将幅值为25 V的直流偏移添加到A相的采样电压中。

图7和图8分别显示了传统方法和考虑直流偏移方法识别得到的电网阻抗。可以看出，当使用常规方法时，识别得到的电网阻抗中会出现高频纹波。这主要是因为常规CCF无法完全消除直流偏移带来的影响。

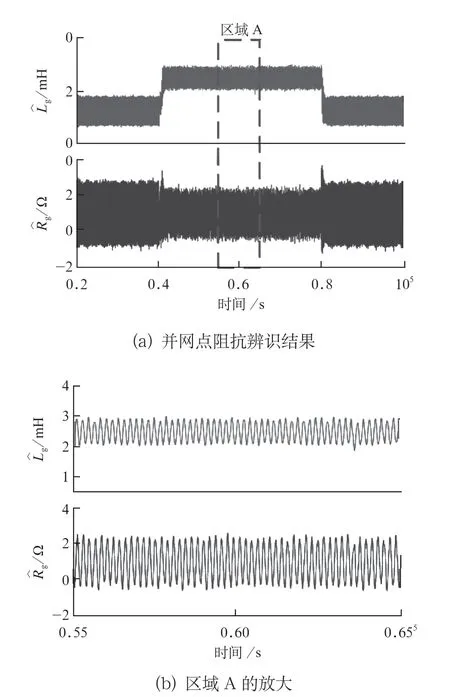
图7 常规CCF得到的并网点阻抗

图8所示为考虑直流偏移CCF得到的并网点阻抗，可以看出，此时CCF可以完全消除了直流偏移的影响，并识别获得了准确的电网阻抗。

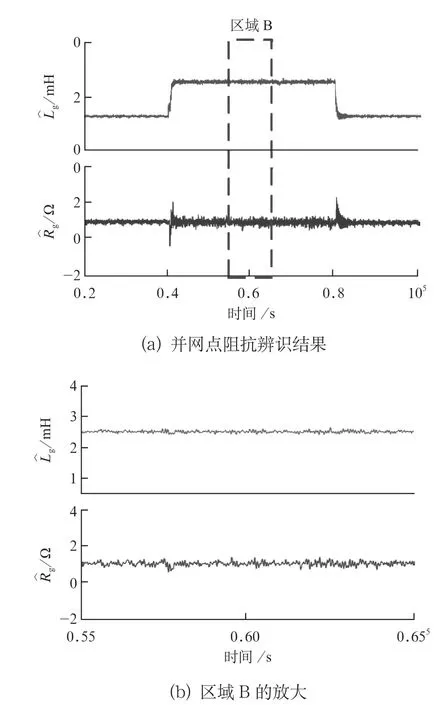
图8 考虑直流偏移CCF得到的并网点阻抗

为了进一步显示所提出的CCF的有效性，采用两种CCF分别提取高频电压和电流，如图10，11所示。其中图9是采用常规CCF，图11是采用考虑直流偏移的CCF。

从图9可以看出，采用常规CCF时，受直流偏置的影响，提取的电压uβh与uαh相比，uβh明显的向上偏移，无法准确的识别检测电网阻抗。

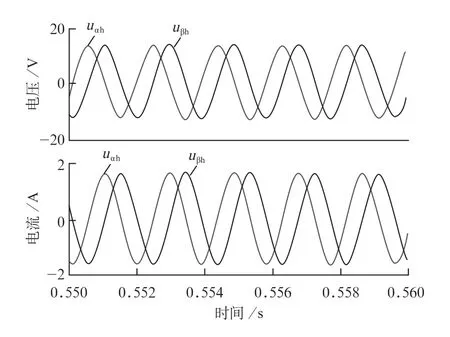
图9 常规CCF提取的电压电流

图10中，所提出的CCF完全消除了直流偏移的影响，提取的电压不包含直流分量，uβh与uαh平衡，可以准确地识别检测电网阻抗。

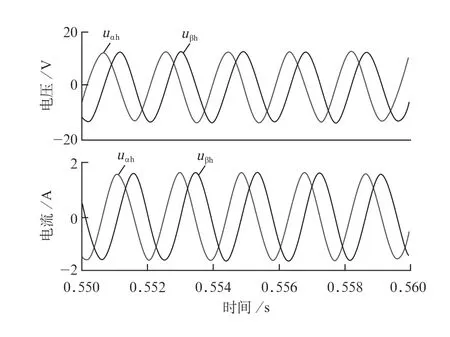
图10 考虑直流偏移CCF提取的电压电流

为进一步验证文中提出的方法对于直流偏移抑制的有效性，进行直流偏移动态仿真。首先进行电压动态仿真，在此仿真中，Lg设置为2.4 mH，Rg设置为1 Ω。开始时向A相注入的直流偏移电压设置为25 V，在0.4 s时升至50 V。

图11是基于所提出的CCF提取的高频电压和电流。可以看出，0.4 s时直流偏移增大，CCF提取的高频电压中会产生直流分量。经过短暂的瞬态过程后，直流分量消失，并且达到了新的稳态。

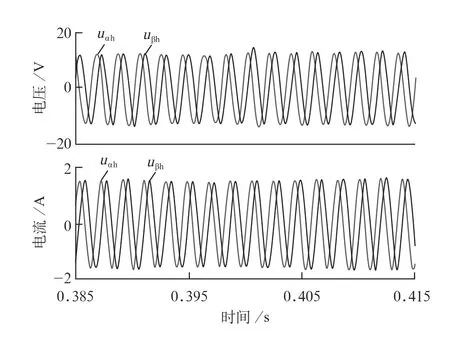
图11 考虑直流偏移CCF电压动态变化时提取的电压电流

图12显示了当A相的直流偏移电压从25 V升至50 V时识别的电网电阻和电网电感。可以看出，即使直流偏移突然升高，CCF也可以精确识别电网电阻和电感，表明了所提出CCF对直流偏移的抑制能力。

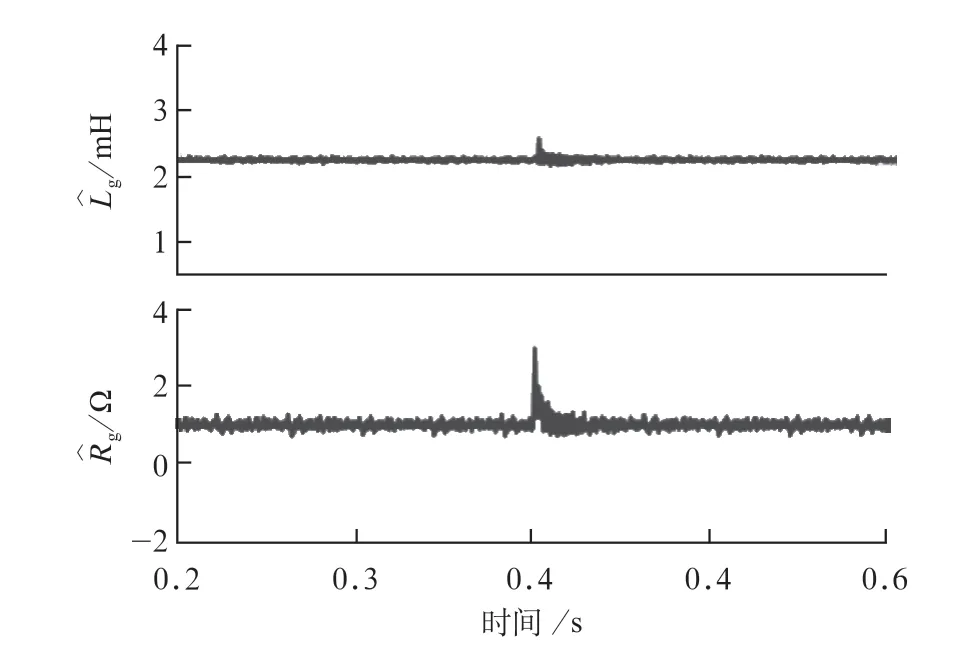
图12 考虑直流偏移CCF在电压突变时识别的电网阻抗

进行电流变化时的直流偏移动态仿真，Lg设置为2.4 mH，Rg设置为1 Ω。注入A相的直流偏移电压设置为25 V，初始注入电流设置为10 A，0.4 s时注入电流升至40 A。仿真结果显示当电流突然升高时，识别的电网阻抗会产生动态误差，经过短暂的瞬变过程，识别的电网电阻和电感会收敛到一个稳定值。验证了所提出的电网阻抗识别方法的有效性。

4 结束语

为了更准确地识别电网阻抗，消除直流偏移对电网阻抗识别的影响，提出了一种改进的CCF电网阻抗检测方法。首先分析了常规CCF的滤波器特性，结果表明常规方法无法消除直流偏移的影响。因此，将高通滤波器添加到其前向通道中，构建了一种考虑直流偏移的CCF电网阻抗识别方法。分析推导了所提出CCF的传递函数和滤波特性并进行了仿真验证。搭建了基于MATLAB/Simulink的仿真系统，对比验证了考虑直流偏移影响的CCF电网阻抗识别方法的有效性。