基于改进飞蛾算法的电动汽车充电站选址研究
2021-10-23张强毛清华梁萍
张强,毛清华,梁萍
(燕山大学 经济管理学院,河北 秦皇岛,066004)
随着中国经济的快速发展,私人汽车拥有量逐年提升,由此引发的化石能源过度消耗和环境污染问题日益突出,为了响应“节能减排,低碳环保”的号召,零排放的电动汽车迅速崛起并成为未来发展趋势。为了促进电动汽车市场发展,满足电动汽车用户的充电需求,提高社会综合效益,解决充电基础设施建设落后、充电站网络不健全、充电站选址不合理等发展问题迫在眉睫。
目前充电站选址模型可分为3 类:第1 类仅考虑运营商或者用户,目标函数包括盈亏平衡年限[1]、距离满意度与引力因素[2-3]、覆盖需求[4]等;第2 类基于商家和用户博弈的两维视角构建模型,目标函数包括充电站建设成本、用户广义充电成本[5]、绕行距离成本[6]等;第3 类基于利益相关者视角构建模型,考虑主体包括运营商、用户、电网企业、社会等,目标函数扩展到道路负荷[7-8]、低碳收益[9]、电网负荷[10]等。此外还有研究通过多准则决策评价方法[11-12]、直觉或多层次模糊评价方法[13-14]、不确定语言多属性决策方法[15]进行决策选址。充电站选址属于NP-hard 问题,目前模型求解大多采用传统的智能优化算法,如遗传算法[16]、粒子群算法[17-18]、禁忌搜索算法[19]等,但遗传算法收敛速度慢并且容易陷入局部最优解,粒子群算法收敛速度快但容易陷入局部最优,禁忌搜索算法全局开发能力弱。针对传统智能算法的缺陷,Mirjalili[20]提出了一种新颖的智能优化算法—飞蛾火焰算法(MFO),该算法具有参数少和鲁棒性强的优点,迅速应用于多晶硅太阳能电池/模块二极管模型参数提取[21]、特征选择的机器学习领域[22]、无功优化调度方案[23]、求解数值和约束工程优化问题[24]等优化问题。
综上所述,目前研究主要基于成本、费用、收益等经济性指标建立模型,追求成本最小化和收益最大化,并多采用传统智能算法进行求解。本文拟建立以充电站年建设运行维护成本及用户前往充电站耗时成本之和的全社会总成本为优化目标,以充电需求、等待时间为约束条件的充电站选址模型,并创新性提出一种改进的飞蛾火焰算法进行求解。本文不仅延展了飞蛾火焰算法的应用领域,而且通过优化提升了算法的求解能力。
1 电动汽车充电站选址模型构建
1.1 问题描述
充电站的首要任务是尽量多地满足用户的充电需求,充电站数量越多,用户满意度越高,但是建设成本也会随之增加。因此需要在较好满足充电需求的同时,严格控制充电站建设数量,充电站选址规划是平衡以上矛盾的有力手段。为方便建模,作出以下假设:
(1) 就近原则,即每个需求点只选择最近的充电站接受充电服务,且匀速行驶;
(2) 每个需求点代表一个区域,需求点对应的需求数量代表该区域电动汽车总数量;
(3) 不考虑充电站的建设等级,充电站内充电桩均为快速充电桩,不考虑慢速充电桩;
(4) 每个充电站的快速充电桩规格相同,服务能力无差异;
(5) 充电站内接受充电服务时,执行“一桩一车”制,一台充电桩不能同时为多辆电动汽车充电。
1.2 数学模型构建
首先给出一些字母表示:I表示需求点集合;i表示需求点编号,i∈I;J表示充电站候选点集合;j表示充电站候选点编号,j∈J;qi表示需求点i的充电需求数量;Nj表示充电站j的充电桩数量;dij表示需求点i到候选点充电站j的距离;O表示固定投资费用,包括土地成本,建筑等成本;µ表示充电站购置充电桩等设备和修建成本的等效投资系数;cij表示用户前往充电站的单位耗时成本;H表示充电站的建站数量;β表示购置充电桩的单价;α表示运营维护成本与建设成本之间的折算系数;V表示电动汽车的行驶速度;τ表示城市道路拥堵系数;Nj表示购置充电桩的数量;Nmin表示充电桩的最小数量;Nmax表示充电桩的最大数量;n表示充电站使用年限;r0表示贴现率。yj={0,1}表示0-1 决策变量,1 表示在候选点j建立充电站,反之取0,Yij={0,1}表示0-1 决策变量,若需求点i前往候选站点j进行充电其值取1,反之取0。
目标函数主要由充电站建设成本C1、年运营维护成本C2及用户前往充电站耗时成本C33 部分组成的全社会总成本MinF=C1+C2+C3。
建设成本C1包括固定投资成本和可变成本,固定投资成本涉及土地成本、建筑材料成本以及修建道路本等,可变成本指充电桩购置费用,
年运行维护成本C2包括职工工资和维修成本等,
1.3 数学模型表达式
电动汽车充电站多目标函数选址模型

约束条件:

式(1)表示全社会年总成本最小化;式(2)表示在候选点j处建站时,才能满足用户需求;式(3)表示所建立的充电站能够满足所有需求点的充电需求;式(4)表示每一个需求点只能去唯一的充电站接受充电服务;式(5)表示拟建站的数量;式(6)表示充电桩数量的约束条件;式(7)表示在充电站j等待的时间小于等于规定值。
其中,等待时间tj可以运用排队论的方法计算[25]。假设电动汽车到达充电站的过程服从泊松分布,充电桩的服务过程服从负指数分布,则电动汽车的排队等待时间为

其中:tj表示等待时间;ρj表示充电站候选点j的充电桩服务强度;λ表示平均每小时到达充电站的汽车数量;ε表示每个充电桩单位时间的服务数量;P0表示充电站的空闲概率。
2 飞蛾火焰算法及其改进
2.1 基本飞蛾火焰算法
基本飞蛾火焰算法步骤如下:
步骤1:初始化MFO 算法的参数,设置种群数量n′、迭代次数L和对数螺旋形状常数b等参数;
步骤2:将飞蛾位置按照适应度值大小排序,并赋值给火焰,形成火焰的空间位置;
步骤3:更新围绕火焰飞行的飞蛾位置,公式为

步骤4:记录当前火焰适应度值并排序,将更优的适应度值对应的位置作为下一代火焰的位置;步骤5:自适应减少火焰数量,公式如下:

其中:Z表示火焰数量的最大值;l为当前迭代次数;L表示最大迭代次数。
2.2 改进的飞蛾火焰算法(IMFO)
2.2.1 改进的自适应火焰更新公式
通过改变弃焰行为公式,将火焰数量更新机制由直线下降改为曲线下降,可以提高自适应火焰数量的收敛速度,进而加快算法的收敛速度。改进后的火焰更新公式为[26]

2.2.2 改进的对数螺旋函数
借鉴粒子群算法中的惯性权重思想,引入自适应权重,在飞蛾靠近火焰寻找最优解时,自适应权重值减小,则飞蛾的局部寻优能力将得到提高。自适应权重ω的计算公式为[27]

将自适应权重应用到飞蛾更新位置式(9)中:D1i=M i-F j,D2i=Gi-Fj,其中Gi为种群历史最优个体的位置。有

2.2.3 高斯变异
高斯变异(GM)策略源自高斯正态分布,高斯变异可以在原始父母附近产生新的后代,借助这一特性,可以增加飞蛾和火焰的多样性,进一步提升局部搜索能力和收敛速度。

式中randn 为服从高斯分布的随机数。
2.2.4 融合模拟退火算法
为避免算法陷入局部最优,进一步对算法进行改进。模拟退火算法具有一定概率接受劣解的特点,故可以跳出局部最优解,可解决MFO 算法陷入局部最优解的问题。具体步骤如下:
(1) 初始化:设定初始温度t0,任取初始解S1,确定每个t的迭代次数;
(2) 对当前温度t,重复步骤(3)~(6);
(3) 给当前解S1随机扰动,得到新解S2;
(6) 判断是否达到终止条件,满足条件输出最优解,否则,对温度t降温,返回步骤(2),直到没有接受新解S2或达到终止温度。
改进飞蛾火焰算法流程图如图1 所示。
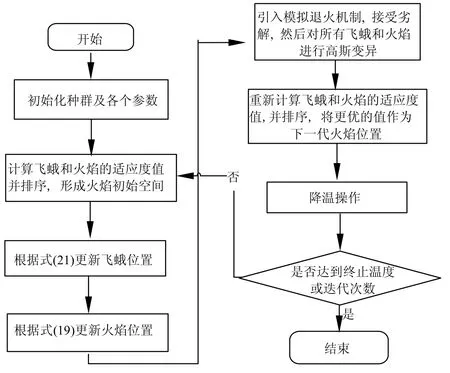
图1 IMFO 算法流程图
2.3 算法性能测试
基于6 个基准测试函数,比较IMFO 算法、遗传算法(GA)[16]、粒子群算法(PSO)[17]和MFO的性能,测试函数中包括单峰函数和多峰函数。为公平验证IMFO 算法有效性,测试在同一运行环境下进行,运用MATLAB2019a 版本完成仿真,CPU:Inter(R)Core (TM)i5-3230M CPU@2.60GHz 2.600GHz,操作系统:Microsoft Windows 8.1,通用条件设置为相同,种群数量为50,迭代次数为500。
2.3.1 参数设置
各个算法的参数设置如表1 所示,基准测试函数见表2(f1~f3为单峰函数,主要测试算法的收敛速度;f4~f6为多峰函数,主要测试算法跳出局部最优的能力和收敛精度)。

表1 参数设置表

表2 基准测试函数
2.3.2 算法收敛曲线比较分析
基准测试函数曲线能够直观地体现各个算法的收敛速度和收敛精度,同时也能清楚地显示算法跳出局部空间的能力。6 个基准测试函数的收敛曲线如图2~7 所示。

图2 f1 收敛曲线
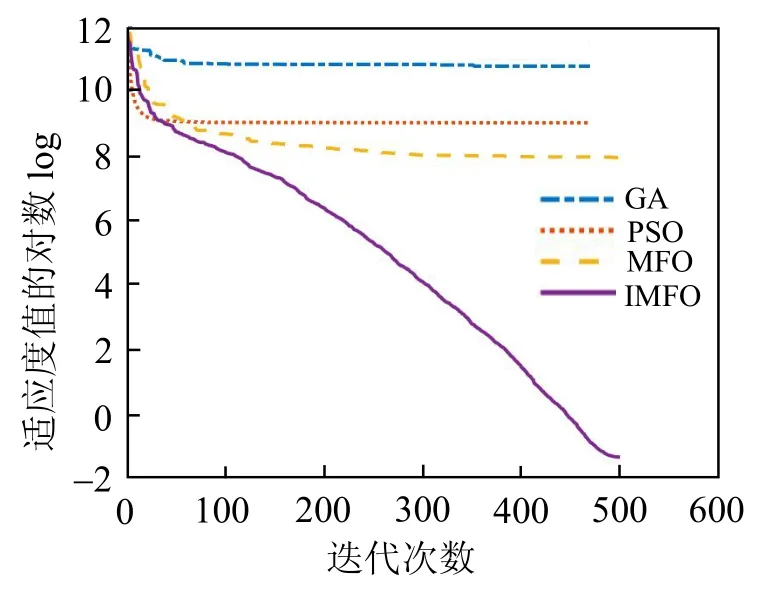
图3 f2 收敛曲线

图4 f3 收敛曲线

图5 f4 收敛曲线

图6 f5 收敛曲线

图7 f6 收敛曲线
由收敛曲线图2~7 可知,IMFO 具备更优的收敛性能,其收敛曲线更加平滑,较大的拐点很少。与其他3 种算法相比,IMFO 收敛精度更高,收敛速度更快。曲线特征说明IMFO 能够有效地跳出局部最优,进而向全局最优解快速收敛,全局搜索能力得到有效提高,因而可以有效地求解单目标优化问题。
3 算例研究
3.1 测试实例
为了验证模型和算法的有效性,本文选取某个区域为例,在一个平面区域[0,50]×[0,50]内设计了一个有30 个需求点和15 个备选站点的测试实例。区域内候选点和需求点的位置及相应的需求量如表3 所示。算例中,充电站固定投资O为100万元充电桩单价β为10 万元/台,每个充电站充电桩建设数量Nmin为4 台,Nmax为20 台,充电站购置充电桩等设备和修建成本的等效投资系数µ为2 万元/台,1 台充电桩每小时可服务2 辆电动汽车单位耗时成本cij为10 元/h,城市道路拥堵系数τ为1.2,充电站的折旧年限n为20 年,贴现率r0为0.08,充电站年运营维护成本与建设成本之间的折算系数α为0.1,拟建设充电站数量H为6座,算法中种群数量设置为50,迭代次数为300 次。

表3 需求点及候选点位置坐标及需求数量
3.2 结果分析
IMFO 选址结果分别如表4 和图8 所示,MFO 选址结果见图9。

表4 IMFO 算法选址结果信息

图8 IMFO 选址图
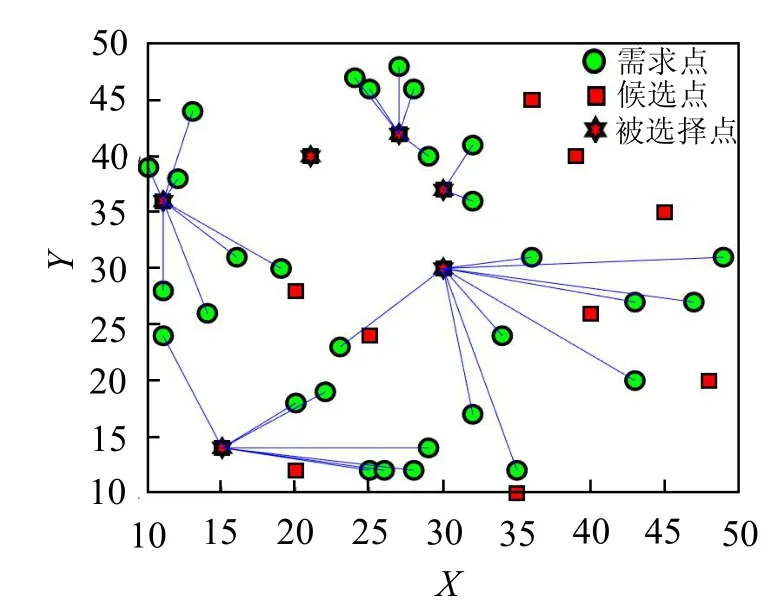
图9 MFO 选址图
为了进一步验证IMFO的性能,将其与已有文献采用的GA[16]、PSO[17]进行比较,4 种算法迭代曲线比较如图10 所示。
由图10 可知,在同一运行环境下,PSO的收敛速度最快,IMFO 收敛速度相对较慢,但是收敛精度远高于其它算法,GA 精度次之。这说明了其它几种算法在迭代一定次数时,均已陷入局部最优的情况,IMFO 融合了模拟退火思想和高斯变异操作,提升了跳出局部最优解的能力,避免了陷入局部最优,虽然计算时间更长,但是收敛精度最高,计算结果更优,获得的总成本最低。结合图10 和表4 可知,IMFO是一种能够有效地解决电动汽车充电站选址问题的高效算法。

图10 4 种算法收敛图
3.3 灵敏度分析
进一步对充电站的建设数量与优化目标间的关系进行分析,如图11 所示。
由图11 可知,随着充电站建设数量的增加,用户前往充电站的耗时成本逐渐减少,用户的满意度会越来越高,在资金允许的情况下,可以通过增加建站数量来提高用户的满意度。

图11 建站数量与耗时成本C3的关系
4 结论
本文创新性提出一种改进的飞蛾火焰算法,并基于基准测试函数,与GA、PSO 及MFO 进行了性能比较,然后利用IMFO 求解电动汽车充电站选址模型,得出以下结论:
(1) 兼顾用户与运营商双方利益,构建以年社会总成本为优化目标,考虑等待时间约束,建立充电站选址模型,具有一定的借鉴意义;
(2) 创新性提出一种改进的飞蛾火焰算法。以基本飞蛾火焰算法为框架,将自适应火焰数量更新机制沿直线下降改为曲线下降,加快算法收敛速度;引入自适应权重与高斯变异策略,改变飞蛾位置更新方式,提高了算法局部搜索性能;结合模拟退火算法的概率突跳能力,避免算法陷入局部最优,提升全局寻优能力;
(3) 基于基准测试函数发现,IMFO 算法相比GA、PSO 及MFO 具备更好的收敛性能,能够跳出局部最优,收敛精度更高。求解电动汽车充电站选址模型发现,IMFO 具有更好的寻优性能,能够高效地求解电动汽车选址问题;
(4) 后续研究,可以将道路拥堵情况、用户选择行为等因素纳入模型中考虑,或者从新的利益相关方视角建立优化目标,在求解模型算法上,可以寻找一种更为高效的算法,也可将此算法与其它智能优化算法进行融合,求解其它优化问题,扩大算法的应用范围。
