砂砾岩油藏影响压裂效果关键地质力学因素研究及应用

2021-10-23林海宇刘向君王小军梁利喜

石油地球物理勘探 2021年5期

熊健林海宇唐勇刘向君* 王小军梁利喜

(①西南石油大学油气藏地质及开发工程国家重点实验室，四川成都 610500；②中石油新疆油田公司勘探开发研究院，新疆克拉玛依 834000)

0 引言

近年来，针对准噶尔盆地砂砾岩油藏的勘探开发取得重要突破，特别是玛湖凹陷三叠系百口泉组以及二叠系上乌尔禾组砂砾储层有着巨大的勘探开发潜力[1-2]，其中二叠系上乌尔禾组为扇三角洲沉积，整体为一套由砾岩、泥岩组成的超覆退积的粗粒碎屑岩体,地层厚度为0～300m[3]。目前，针对该储层进行的大量研究主要集中在沉积特征[4-6]、成藏控制因素[7]、成岩作用特征[8-10]、储层特征[11-13]、储层预测[14-15]等方面，取得的研究成果有效支撑了玛湖凹陷二叠系上乌尔禾组砂砾岩储层的勘探与开发。

地质工程一体化技术是致密砂砾岩油藏实现效益开发的有效途径[16-17]，已经在新疆油田玛湖凹陷三叠系百口泉组致密砂砾岩油藏开发中得到应用并取得了良好的效果，目前正逐步在该区乌尔禾组致密砂砾岩油藏开发中推广应用[18]。地质力学参数在地质工程一体化中起桥梁作用，能确保地质认识和工程技术无缝衔接，切实解决工程难题[19]。储层地质力学参数一般涉及岩石力学、孔隙压力、地应力等方面，是井位优选、钻井井壁稳定、储层改造等环节的关键参数。目前，国内外学者对煤岩、页岩、砂岩、碳酸盐岩、砂砾岩等储层[20-26]的地质力学规律已有较多研究，并取得了一定的认识。为了更好地开发玛湖凹陷乌尔禾组油藏，有必要对乌尔禾组砂砾岩储层岩石地质力学特性展开深入研究，掌握储层地质力学规律。

体积压裂也是高效开发致密砂砾岩油藏的技术方法之一[16-17]，压裂效果很大程度上决定了油气产能，开展影响压裂效果主控因素的研究对优选砂砾岩储层压裂井段、设计砂砾岩油藏开采方案等具有重要的经济价值。之前，学者针对页岩气藏、煤层气藏、致密油藏、砂砾岩油藏等多种类型储层的压裂效果评价方法做了大量的研究工作[27-29]，杨兆中等[30]基于Apriori关联分析法研究了压裂施工工艺参数对煤层气压裂效果的影响，并优化了压裂施工参数；李玉伟等[31]利用模糊综合评判与灰色关联方法分析了水平井储层参数与压后日增产量的关联程度；李小刚等[32]基于灰色关联法分析了储层因素和压裂施工工艺因素对砂砾岩储层压后产能的影响程度；龙章亮等[33]基于灰色关联法分析了页岩储层中储层、压裂施工工艺和力学参数等共12个因素对无阻流量的影响程度，提出了一种可压指数。这些研究从储层地质因素或压裂施工工艺因素等方面研究了影响压裂效果的各个因素之间的主次关系，对压裂优化设计具有一定的借鉴意义。然而，在影响压裂效果的主控因素评价中，考虑储层地质力学因素的研究和认识相对较少。

为此，开展了针对乌尔禾组砂砾岩储层影响压裂效果关键地质力学因素相关研究。本文以玛湖凹陷乌尔禾组砂砾岩储层岩石为研究对象，基于室内同步的物理实验和岩石力学实验，构建了乌尔禾组岩石力学参数测井预测模型；基于已钻井压裂、测井资料，建立了乌尔禾组地层孔隙压力、地应力测井预测模型，在此基础上，结合油井压后产能资料，采用灰色关联法得到了各地质力学参数与米采液指数(指在单位生产压差下单位厚度储层的日产液量)的关联程度。之后，采用层次分析法构建了储层压裂工程评价指标计算模型，为储层压裂优化设计提供了依据。

1 储层地质力学特性

1.1 岩石力学特性

储层地质力学的研究范围涉及储层岩石力学、地层孔隙压力、地应力等方面，其中储层岩石力学性质是储层地质力学研究的基础。为了获取储层段岩石力学特性，需建立基于测井信息的岩石力学参数计算模型，进而得到单井岩石力学参数剖面。目前已建立的不同地区、不同岩性的岩石力学参数经验公式，使用范围存在局限性[34]。因此，需要建立针对玛湖凹陷乌尔禾组砂砾岩储层的岩石力学参数的测井计算模型。

以乌尔禾组砂砾岩储层井下岩石样品为研究对象，对岩样进行基础物性测试。通过声波和强度同步测试系统[35]对岩样进行测试和筛选。力学测试主要包括单轴抗压强度(12块岩样)、三轴压缩测试(10块岩样)和巴西劈裂测试(12块岩样)，并且对全部岩样进行体积密度和超声波测试。测量结果如表1所示。

表1 乌尔禾组砂砾岩储层岩石样品力学参数测试结果

基于测试结果，建立了乌尔禾组储层岩石力学参数与声波、体积密度之间的关系，图1a～图1c分别显示岩石单轴抗压强度、岩石抗张强度、岩石弹性模量与声波时差/密度(1/IP)呈明显的负相关性；图1d显示岩石泊松比与声波时差/密度(1/IP)间呈明显的正相关性，并分别拟合出各自的相关公式。根据储层岩石力学参数的响应机制，建立了储层岩石力学参数的测井计算模型。

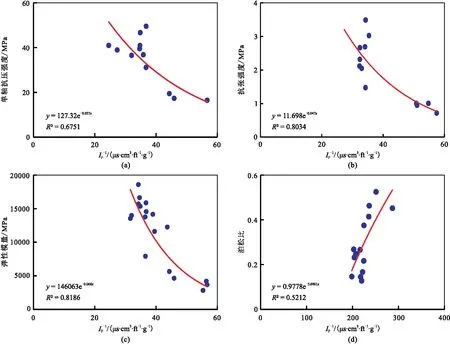
图1 岩石力学参数与声波、密度间的关系

同时，基于应力—应变曲线建立的岩石脆性指数计算方法[36]，获取了乌尔禾组储层岩石脆性指数的范围(16.96～62.20)和平均值(37.90)。在此基础上，研究了乌尔禾组储层脆性指数与岩石力学参数、声波、体积密度间的关系(图2)，并建立储层岩石脆性指数的测井计算模型。由图可见，岩石脆性指数与静态弹性模量呈明显的正相关性。

图2 脆性指数与弹性模量间的关系

1.2 地层孔隙压力

准确预测地层压力对优质高效安全钻井、储层压裂改造等具有重要的意义。目前，预测地层压力的方法有多种，其中基于测井资料预测地层孔隙压力最为常用，又大致分为等效深度法、Eaton(伊顿法)和有效应力法三种。前两种方法需要建立正常压实趋势线，主要考虑声波、电阻率、自然伽马等单因素的影响；有效应力法通过建立有效应力与测井岩石物理响应的关系预测地层孔隙压力，该方法综合考虑了多种因素的影响，可避免单因素导致的精度低、误差大的问题[37]。利用地层孔隙压力实测数据及相应井段的测井数据进行多元非线性回归分析，可得到有效应力计算模型

σe=0.00556DEPTH+0.09717AC+

11.2367lnGR-64.7978

(1)

式中：DEPTH为地层深度；AC为声波时差值；GR为自然伽马值。

基于测井资料和式(1)得到计算有效应力值，与实测有效应力作对比(图3)可以看出，计算有效应力值与实测有效应力值非常接近，说明模型具有较高的精度，能够满足工程需求。基于有效应力理论，结合密度测井资料，得到乌尔禾组储层地层压力计算公式

图3 实测有效应力值与计算有效应力值间的关系

(2)

式中：σV为垂向应力；H0为测井起始点深度；ρ0(h)为未测井段深度为h点的密度；ρ(h)为深度为h点的测井密度；g为重力加速度，取9.8 kg·m/s2。

1.3 地应力

储层地应力是钻井工程及压裂工程所需的基础参数，对研究区油气勘探与开发具有重要意义。确定地应力参数的方法有很多，其中基于水力压裂资料反演是测量深部地层应力最有效的方法，也是国际岩石力学测试技术委员会推荐的岩体应力测量的主要方法之一[38]。该方法基于压裂施工曲线得到地层的破裂压力和闭合压力，进而计算得到某深度点地层水平最小主应力和水平最大主应力。在此基础上，结合式(3)弹簧组合模型获取该深度点的构造应变系数，并获得单井的地应力剖面。利用该方法计算得到乌尔禾组储层的沿最大主应力方向与最小主应力方向构造应变系数平均值分别为6.497×10-3和2.106×10-4，利用式(3)即可获得该储层的地应力计算模型。

(3)

其中

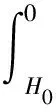
(4)

式中：σH、σh分别为水平最大、最小主应力；α为biot系数；εH、εh分别为沿最大主应力方向与最小主应力方向构造应变系数。

基于以上构建的岩石力学参数计算模型、孔隙压力计算模型和地应力计算模型，结合测井资料，可得到单井乌尔禾组储层段地质力学剖面图。图4为玛湖凹陷A井的地质力学参数剖面图，综合统计研究区已钻井的单井计算结果，可得到研究区乌尔禾组储层岩石单轴抗压强度范围为33～48MPa，抗张强度范围为3.86～7.94MPa，弹性模量范围为12016～19887MPa，泊松比范围为0.30～0.34，脆性指数范围为22～42，乌尔禾组储层地层压力主要范围在1.07～1.41MPa/100m。乌尔禾组储层主要以潜在正断型地层为主，即，其中垂向应力梯度范围为2.35～2.36MPa/100m，水平最大主应力梯度范围为1.91～2.10MPa/100m，水平最小主应力梯度范围为1.71～1.86MPa/100m。

图4 A井砾岩段地质力学参数剖面图(3675～3708m)

2 影响压裂效果的主控因素分析

影响压裂效果的储层地质力学因素包括单轴抗压强度、抗张强度、弹性模量、泊松比、地层压力、水平最大主应力、水平最小主应力和水平应力差等9个参数。压裂效果评价主要采用米采液指数法，其值越高，压裂效果越好，反之压裂效果越差。从射孔压裂段提取每段地层的地质力学参数，并分析影响因素与压裂后的米采液指数间的关联程度。由于不同的影响因素存在量纲和数量级的差异，因此需采用极值变换法对各影响因素的原始数据进行无量纲化处理，即

(i=1,2,…,m;k=1,2,…,n)

(5)

式中:Xi(k)为第i个影响因素中的第k个值；Yi(k)为第i个影响因素中的第k个值的归一化值；m、n分别为影响因素个数和数据点个数。

图5分析了归一化后各影响因素与米采液指数之间的关系，可以看出，脆性指数、弹性模量与米采液指数呈正相关(图5c、图5d)，即影响因素值越大，米采液指数越大，储层压裂效果越好；单轴抗压强度(图5a)、抗张强度(图5b)、泊松比(图5e)、水平应力差(图5j)与米采液指数呈负相关，即影响因素值越大，米采液指数越小，储层压裂效果越差；地层压力、水平最大主应力、水平最小主应力与米采液指数没有明显的相关性(图5f～图5h)。另外，图中还可以看出，虽然各影响因素与米采液指数之间存在线性相关，但是相关系数较低，因此本文只是定性评价各影响因素对压裂效果的影响，没有进行定量评价。

图5 归一化地质力学参数与米采液指数间的关系

刘会虎等[27]、李玉伟等[31]、李小刚等[32]、龙章亮等[33]采用灰色关联法对影响煤层气藏、页岩气藏、致密油藏和砂砾岩油藏压裂效果的主控因素进行了研究，认为灰色关联法是分析影响储层压裂效果主控因素的有效方法。该方法是一种多因素统计分析方法，可通过求解未知的非线性问题中各影响因素的灰色关联度，反映各因素对目标函数的重要性，从而确定各影响因素的主次。通过计算得到影响压裂效果储层地质力学影响因素的指标权重，避免了人为经验确定各影响因素指标权重的主观性。因此，本文采用灰色关联分析法确定影响乌尔禾组储层压裂效果的地质力学主控因素。

采用式(5)对各影响因素和米采液指数数据进行归一化处理之后，对数据进行关联度计算与分析。利用式(6)计算各影响因素的关联系数

(6)

式中：ξi(k)为第i个影响因素的第k个参考点的关联系数；Δi(k)=|X0(k)-Xi(k)|,为归一化后第i个影响因素值(Xi(k))与参考数列值(X0(k))差值的绝对值；d为分辨系数，一般情况取0.5。

将米采液指数设为参考数列，各影响因素设为比较数列，通过计算位移差评价比较数列(各影响因素)与参考数列(米采液指数)之间的相似程度。位移差越小，关联度越接近1，则比较数列和参考数列形态越接近；反之，两者的相似程度越低。

对各影响因素的关联系数进行均值化处理，所得平均值能够定量反映各影响因素的关联程度，计算公式为

(7)

式中：γi为第i个比较数列的关联度；n为该数列中参考点总数。

根据关联度大小排序可确定研究区乌尔禾组储层各因素对压裂效果的影响程度，结果如表2所示。可以看出，各影响因素的关联度数值存在明显差异，与关联度对应的各因素对压裂效果的影响程度由大到小排序依次为水平应力差、脆性指数、弹性模量、抗张强度、单轴抗压强度、水平最大主应力、水平最小主应力、地层压力、泊松比。结合图4可知，水平最大主应力、水平最小主应力、地层压力、泊松比等4个影响因素与米采液指数的相关性较低，判别系数R2都较小(R2<0.12)，且对压裂效果的影响排序偏后，因而综合判断这些因素对米采液指数影响不显著，应予以排除。因此，乌尔禾组储层影响压裂效果的地质力学主控因素为水平应力差、脆性指数、弹性模量、抗张强度以及单轴抗压强度。

表2 各影响因素与米采液指数的关联度及排序

3 储层压裂工程评价指标

可压裂性评价指数对储层的工程甜点评价具有重要意义，已有大量学者进行了相关研究，在构建储层压裂性评价指标中常用层次分析法确定各因素的权重系数。唐颖等[39]、赖富强等[40]、崔春兰等[41]、曾治平等[42]利用层次分析法构建了考虑多种因素的可压裂性评价指标，在针对页岩气、致密气储层的评价中均取得较好的应用效果。层次分析法的基本思想是将所要分析的问题层次化，即根据问题的性质和所要达成的总目标，将问题分解为不同的组成因素，再通过两两比较得出各因素的重要性，建立判断矩阵计算各因素对于目标的权重系数[43]。利用层次分析法确定各因素的权重系数时，需要根据各因素间影响程度关系构造判断矩阵，在基于灰色关联法确定各因素的影响程度排序时，可有效避免人为经验对排序的影响。此外，需要对影响压裂效果的地质力学主控因素进行正向或负向归一化处理，使主控因素都变成正向参数，经归一化后的主控因素越大，米采液指数越大，储层压裂效果越好。其中脆性指数、弹性模量为正相关指标，而水平应力差、抗张强度、单轴抗压强度为负相关指标。本文研究中因脆性指数的预测模型是基于弹性模量建立，因此将脆性指数和弹性模量归为一个影响因素，构建评价指标时只考虑其中之一即可。

根据上述方法，对确定影响乌尔禾组储层压裂效果的主控因素进行对比，衡量各因素的重要性，并应用数字1～9和对应的倒数进行标度，确定各因素的权重，实现了基于矩阵标度法构造判断矩阵(aij表述因素i对因素j的重要性值)，构建的储层压裂工程评价指标判断矩阵如表3所示。在构建判断矩阵的基础上，利用层次分析理论中的特征向量法计算各主控因素的权重向量(权重系数)，得到了研究区水平应力差、脆性指数、抗张强度、单轴抗压强度等因素的权重系数依次为0.41、0.29、0.20、0.10。

表3 储层压裂工程评价指标判断矩阵

基于层次分析法得到的各主控因素权重系数，建立乌尔禾组砂砾岩储层压裂工程评价指标模型

XE=0.41Δσg+0.29Bg+0.20σtg+0.10σcg

(8)

式中：XE为储层压裂工程评价指标；Δσg为归一化水平应力差；Bg为归一化脆性指数；σtg为归一化抗张强度；σcg为归一化单轴抗压强度。

计算的储层压裂工程评价指标与米采液指数关系如图6所示，可见，储层压裂工程评价指标与米采液指数呈明显的正相关性，储层压裂工程评价指标值越大，储层压裂效果越好，米采液指数值越大，说明构建的权重系数具有一定的可靠性。

图6 储层压裂工程分类评价指标和米采液指数的关系

结合研究区已有资料统计结果，将储层压裂工程评价指标划分为四类，从Ⅰ类到Ⅳ类储层压裂工程评价指标值逐渐降低：①Ⅰ类(压裂效果最优)，XE≥0.6；②Ⅱ类(压裂效果次优)，0.43≤XE<0.6；③Ⅲ类(压裂效果较差)，0.3≤XE<0.43；④Ⅳ类(压裂效果差)，XE<0.3。储层压裂工程评价指标与水平主应力差、脆性指数、抗张强度和单轴抗压强度间关系如图7所示。可以看出，储层分类评价指标与脆性指数呈正相关(图7b)，与水平应力差(图7a)、抗张强度(图7c)以及单轴抗压强度(图7d)呈负相关，即储层压裂工程评价指标随着水平主应力差、抗张强度和单轴抗压强度的增加而减小，随着脆性指数的增加而增加。

图7 储层压裂工程评价指标与地质力学参数关系

基于构建的岩石力学参数预测计算模型和孔隙压力、地应力计算模型，获取单井的地质力学参数剖面，结合构建的储层压裂工程评价指标模型，得到玛湖凹陷B井储层压裂工程评价指标单井剖面图(图8)。由图可见，B井储层压裂工程评价指标分类以Ⅱ、Ⅲ类为主，Ⅰ、Ⅳ类较少。该井有两个射孔压裂段，其中评价结果为Ⅱ类的压裂效果明显好于Ⅲ类，说明储层压裂工程评价指标模型具有一定参考性。