基于VMD-SSA的埋地输气管道泄漏声波信号降噪研究
2021-10-23杨兆发
方 超, 杨兆发, 杨 威
(安徽理工大学 电气与信息工程学院, 安徽 淮南 232001)
由于年限较长、地质沉降、化学腐蚀等原因,埋地输气管道经常发生穿孔泄漏而造成爆炸等重大安全事故,造成严重的生命财产损失。因此,对输气管道泄漏检测和精准定位技术的研究具有非常重要的意义。对于大多数埋入地下的输气管道,基于泄漏声波的泄漏点地表检测技术是当前研究的热点。埋地输气管道泄漏声波信号沿土壤介质传播衰减较大,信号幅值、频率均较低[1],采集时极易受周围复杂环境噪声影响。特别是埋于城市周围的管道,通常存在交通噪声、工业噪声等强噪声干扰,造成采集的声波信号失真,影响后续信号处理,有必要对泄漏信号进行降噪处理。
埋地输气管道泄漏声波信号具有典型的非平稳性。小波分析[2]具有时频同时局部化能力,可以较好地刻画信号的非平稳性,常用于信号降噪。小波阈值(Wavelet Threshold, WT)是一种典型的降噪方法,但分解层数和小波基函数的选择对其降噪效果影响很大。2014年,DRAGOMIRETKIY等[3]提出变分模态分解算法(Variational Mode Decomposition, VMD),通过迭代搜寻变分模型最优解来确定信号每个窄带本征模态分量(BIMF)的中心频率和带宽,可实现信号频域带的有效分离。该方法解决了经验模态分解(Empirical Mode Decomposition, EMD)方法的模态混叠、端点效应以及缺乏相关数学理论依据等缺点,同时具有更好的噪声鲁棒性和维纳滤波特性。在较强随机噪声干扰下,VMD去除高频噪声效果良好,但仍然会残留中低频段噪声。奇异谱分析(Singular Spectrum Analysis, SSA)降噪算法[4]稳定性较高、降噪效果较为理想。相较于受阈值函数和小波基影响的小波阈值降噪,SSA法通过选取合适的奇异值进行信号重构,能最大限度地消除噪声并保留有用信息。综上所述,考虑到实际埋地输气管道泄漏声波采集过程中存在较强随机噪声干扰,提出了一种基于变分模态分解和奇异谱分析(VMD-SSA)的联合降噪方法。
1 原理方法
1.1 VMD分解原理
VMD分解过程本质上是变分问题的求解过程[5],目的是在所有模态之和等于输入信号f(t)的前提下使所有模态带宽之和最小。通过估计各模态带宽引出约束性变分模型:
(1)
式中:uk={u1...uK}和ωk={ω1...ωK}分别表示VMD分解的K个模态和其相应的中心频率。
引入Lagrange乘法算子λ(t)和惩罚因子α将上述约束性变分问题转换为非约束性变分问题得到推广的Lagrange表达式。利用乘法算子交替方向法(Alternate Direction Method of Multipliers, ADMM)迭代更新各模态分量及其频率中心,最终求得变分问题的最优解。
1.2 SSA法降噪原理
含噪信号的时间序列l=(l1,l2,…,ln),选择合适的窗口长度W(2 L=USVT (2) 式中:S=diag(λ1,λ2,…,λW),U、V为正交矩阵,λ1,λ2,…,λW为奇异值。 由SSA理论可知信号中的有用分量对应前F个奇异值,噪声分量对应其后数值较小的奇异值。可利用前F个奇异值进行矩阵重构实现信号降噪,选择的F值过小会导致重构信号中有用信号成分丢失,过大则会导致噪声成分增多。 常用的选取F值的方法是奇异值差分谱法[6],其定义为: βi=λi-λi+1,i=1,2,…,W-1 (3) 根据差分谱的定义,有用信号和噪声的相关性不同导致差分谱中产生谱峰,差分谱谱峰蕴含着信噪分离界限。选取最大差分谱谱峰对应的第F个奇异值,将F之后的奇异值置零进行SVD重构即可实现信号降噪。 为了提取含噪泄漏声波信号中的有用信息,需要筛选出VMD分解的有效BIMF分量进行重构。常用的互相关系数筛选原则不适用于原始信号未知的情况,具有一定局限性。本文引入能量熵[7]的变化来判别分解所得BIMF分量中信号与噪声的分界点。确定临界噪声分量的方法是:首先计算从高频到低频各频带模态分量的能量熵;然后根据能量熵分布图找到第一个局部最小值对应的模态即临界噪声分量;最后以该临界分量为界滤除高频噪声分量实现一次降噪。能量熵的计算公式 Hk=-PklgPk (4) 式中:Pk表示第k个模态能量在总能量中的比值。 通过奇异值差分谱理论选取F值重构降噪信号,存在有用信息丢失现象。改进算法结合主成分分析[8]的思想在奇异差分谱理论上增加新的F值选取约束条件,具体步骤如下: (1)VMD分解所得从高频到低频依次排列的各BIMF分量中,噪声对每个模态的支配力逐渐减弱。计算出临界噪声分量的能量E0以及滤除高频噪声分量后剩余BIMF分量的总能量E1,并假设每个BIMF分量中噪声能量为E0,进而估计出剩余模态中的信号能量贡献 R=(E1-d×E0)/E1 (5) 式中:d为剩余BIMF分量数目。 (2)对余下模态重构后进行SSA分析并画出奇异值差分谱,找到每个谱峰对应的奇异值序列fi,计算对应SVD分量的能量贡献Pi(i为奇异值差分谱从左到右的谱峰序号): (6) (3)当首个波峰f1对应的能量贡献小于R时,计算下一个波峰对应的能量贡献,当Pi 埋地输气管道泄漏声波信号VMD-SSA降噪步骤如下: (1)对含噪泄漏声波信号进行VMD分解得到K个BIMF分量,通过不同的K值对应的各个模态中心频率来确定最优分解次数; (2)计算各模态能量熵,根据其分布图筛选出临界噪声分量,以该临界分量为界去除高频噪声模态分量; (3)对余下的模态分量重构之后进行SSA分析,通过奇异值差分谱和能量贡献确定有效奇异值个数F; (4)将F之后的奇异值置零并进行SVD重构得到最终的降噪信号。 通过仿真验证改进F值选取方法的可行性。 构造信号: X=2sin(2π×t)+sin(2π×1 500×t)+0.5×sin(2π×2 500×t) (7) 信号采样点1 024,采样频率1 024 Hz。加入2 dB的高斯白噪声,VMD分解层数为6,惩罚因子为1 000。各模态能量熵分布如图1所示,极小值对应的分量为BIMF4。即BIMF4、BIMF5可视为噪声分量加以去除,前3个含有用信号的BIMF分量重构后进行SSA降噪。根据式(5)计算出余下BIMF分量的信号能量贡献估计值R=0.836。画出奇异值差分谱以及进行SSA降噪前信号频谱如图2所示,计算出前2个谱峰对应的SVD分量的能量贡献为0.648和0.830(均小于0.836),第3个谱峰能量贡献为0.912(大于0.836)。 图1 各模态能量熵分布图 (a)奇异值差分谱 (b)信号频谱 不同F值重构得到的降噪信号频谱如图3所示,依据奇异值差分谱最大峰值点选取的F值为2,结合能量贡献的奇异值差分谱法搜索的F值为6,另外选取F值为5、7做对比。与图2中SSA降噪前信号频谱对比可知:图3(a)中明显丢失了300 Hz、2 500 Hz的频率分量,图3(b)中2 500 Hz频率峰幅值下降了近一半,即F值为2、5重构的降噪信号存在有用信息丢失现象;图3(c)和图3(d)中有用频率成分尖峰都完整保留,图3(c)频谱更加平滑、毛躁减少,计算两者与原始信号的相关度分别为0.961 8、0.954 4,说明本文改进的奇异值差分谱法能搜索最优的F值,能较好的保留有用信号并实现降噪。 埋地输气管道泄漏声波检测实验使用长1.3 m的镀锌钢管模拟管道泄漏部分,管壁预设1.5 mm圆形泄漏孔。模拟输气管道埋土环境,设置埋土深度为80 cm,土质湿度为6%。采集信号的传感器为INV9822通用型压电加速度传感器,放置在土层表面。传感器灵敏度为500 mV/g,频率响应范围为0.2~2.5 kHz,采样率设置为10 kHz。空压机按照1 MPa标准压力为储气罐充气,充满气体后关闭空压机,同时调节减压阀至实验目标压力,直至形成稳定气体泄漏。信号采集装置采集原始泄漏声波信号,将采集数据送至计算机处理。同一实验条件下,开启另一台空压机产生持续的强噪声,用来模拟管道周围复杂的环境噪声。重复上述步骤,进而获得含噪泄漏信号。为了研究不同位置泄漏声波降噪效果的区别,在土层表面设置3个采集点,采集点与泄漏点的空间距离关系为:采集点1<采集点2<采集点3。对各采集点信号截取5 000点(0.5 s)作为降噪算法的输入数据。 按照联合降噪步骤,对采集点1含噪信号进行VMD分解,惩罚因子α设为1 800。不同分解层数的中心频率如表1所示,模态数K为5时各模态中心频率相差较大,发生了欠分解现象;而模态数为7时出现了多个中心频率相近的模态,出现了过分解现象,因此最终选取最优分解次数为6。 表1 不同分解层数的中心频率 根据式(4)计算每个BIMF分量的能量熵,并根据分布图确定BIMF4、BIMF5、BIMF6为噪声分量加以去除。对余下的BIMF分量重构之后进行SSA分析,通过奇异值差分谱结合能量贡献搜索的F值为4,将其后的奇异值置零后进行SVD重构得到最终降噪信号。为了表现改进方法的优越性,使用小波阈值(WT)、变分模态分解(VMD)两种方法进行采集点1的泄漏信号降噪处理做对比。3种方法的降噪信号的时频分析图如图4所示,从上至下依次是WT、VMD、VMD-SSA方法降噪后的波形图与频谱图。 由图4可知,相较于WT方法,改进算法(VMD-SSA)降噪信号的时域波形幅值更加拟合原始信号;WT方法降噪信号在0~500 Hz频段内明显失真,1 500 Hz附近的谱峰被滤去,丧失了部分有用信号成分,且在1 000~2 000 Hz频段仍存在大量噪声;VMD方法降噪信号中高频噪声基本去除,但在1 000~2 000 HZ频段内,VMD方法降噪后存在大量噪点;改进算法可以进一步滤除噪声;相较于WT、VMD方法,采用改进算法的降噪信号和原始信号契合度更高,双谱峰特征明显,较好实现对中低频段噪声的二次滤除。 (a)WT算法降噪信号波形图 (b)WT算法降噪信号频谱图 综上,对于噪声干扰较大的泄漏声波信号,VMD-SSA方法滤除噪声的能力优于其他2种方法。为了研究VMD-SSA方法对不同位置的泄漏声波信号的降噪效果,对采集点2、采集点3的含噪信号进行VMD-SSA方法降噪,画出降噪前后信号的时频幅值图如图5所示。由图5可知两个采集点的降噪信号噪点几乎全部去除,时频幅值图尖峰明显,较好的保留了信号特征。 图5 采集点2、采集点3泄漏声波信号降噪前(左)后(右)时频幅值图 评价降噪效果的指标一般有信噪比(SNR)和均方根误差(RMSE)。降噪信号的SNR越高、RMSE越低表示降噪效果越好。SNR和RMSE的计算公式如下: (8) (9) 式中:f1(n)表示原始信号,f2(n)表示去噪后的信号,N表示信号长度。 定量分析几种方法的降噪性能,分别计算出3个采集点的含噪泄漏声波信号通过小波阈值(WT)、变分模态分解(VMD)以及改进算法(VMD-SSA)降噪前后的SNR和RMSE值,如表2所示。由表2可知对于不同采集点的泄漏信号,VMD-SSA方法相较于WT、VMD方法降噪信号的SNR有明显提高、RMSE有明显下降。计算出3种方法降噪信号的SNR平均提高量和RMSE平均下降量(相较于降噪前),相较于WT、VMD方法,改进算法降噪后的SNR增量分别提升32.3%、21.9%;RMSE减量分别达到17.6%、10.1%。 表2 不同方法降噪性能指标对比 综上所述:对于不同位置噪声干扰下的泄漏信号,WT、VMD方法都有一定的降噪能力,但降噪效果相近,不能表现出明显区别和提高。改进算法(VMD-SSA)的降噪效果明显提高,降噪优越性得到证明。 针对埋地输气管道泄漏声波信号沿土壤介质传播过程中易受强噪声干扰这一问题,提出了变分模态分解结合奇异谱分析(VMD-SSA)的降噪方法。实验分析表明该方法降噪效果良好,主要结论如下: (1)通过能量熵值确定含噪BIMF分量并根据优化F值选取的奇异值差分谱实现进一步降噪,有用信息得到保留的同时,可以有效去除噪声; (2)对于不同位置采集的泄漏声波信号,VMD-SSA法降噪能力较之WT、VMD方法,无论是直观降噪效果还是定量降噪指标都有一定提升; (3)改进方法可以从较强噪声中提取出原始泄漏声波信号,且不会造成信号失真。实验过程契合实际管道泄漏声波面临噪声干扰这一环境,具有一定的实际应用价值。2 VMD-SSA联合降噪算法
2.1 BIMF分量筛选
2.2 有效奇异值数目确定
2.3 联合算法降噪步骤
3 仿真验证
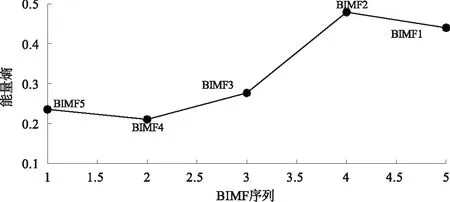
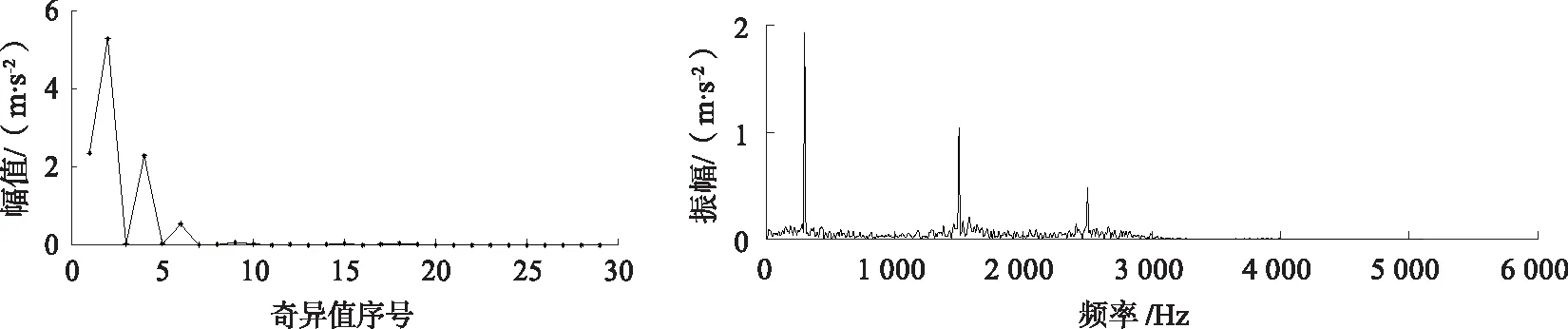
4 实验结果与分析
4.1 VMD-SSA原理验证
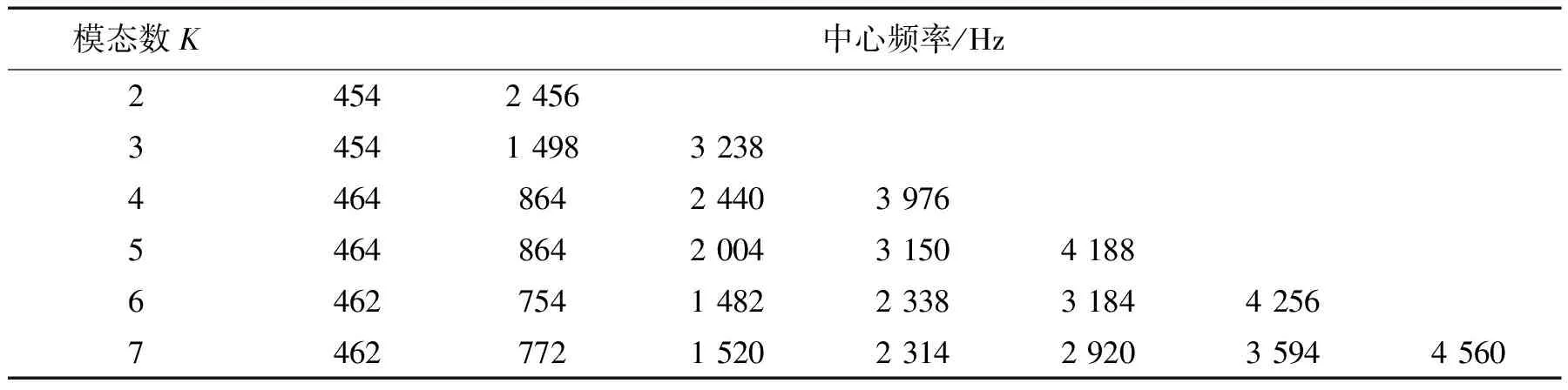
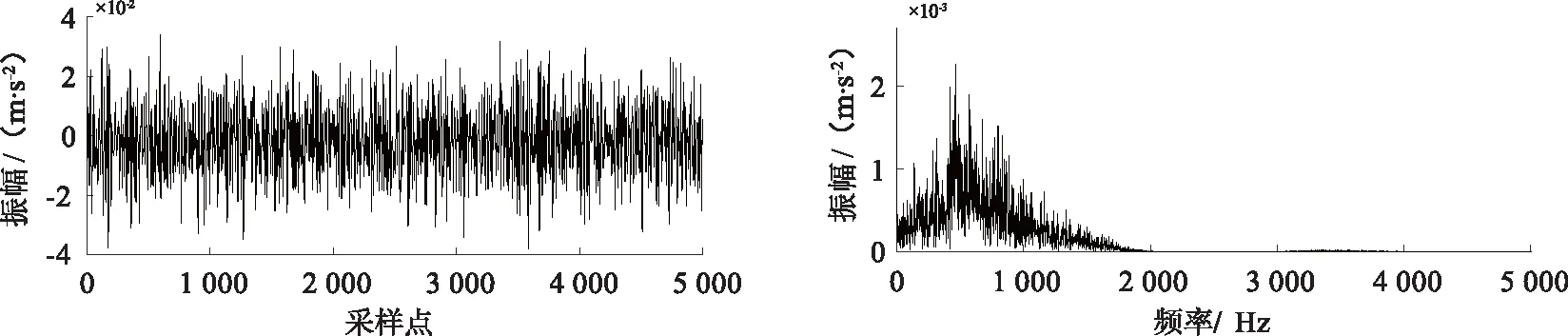
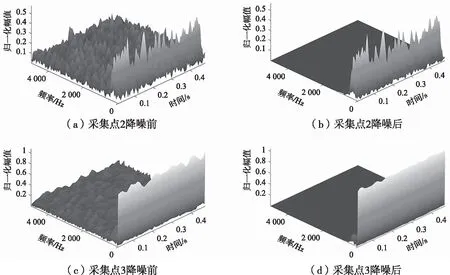
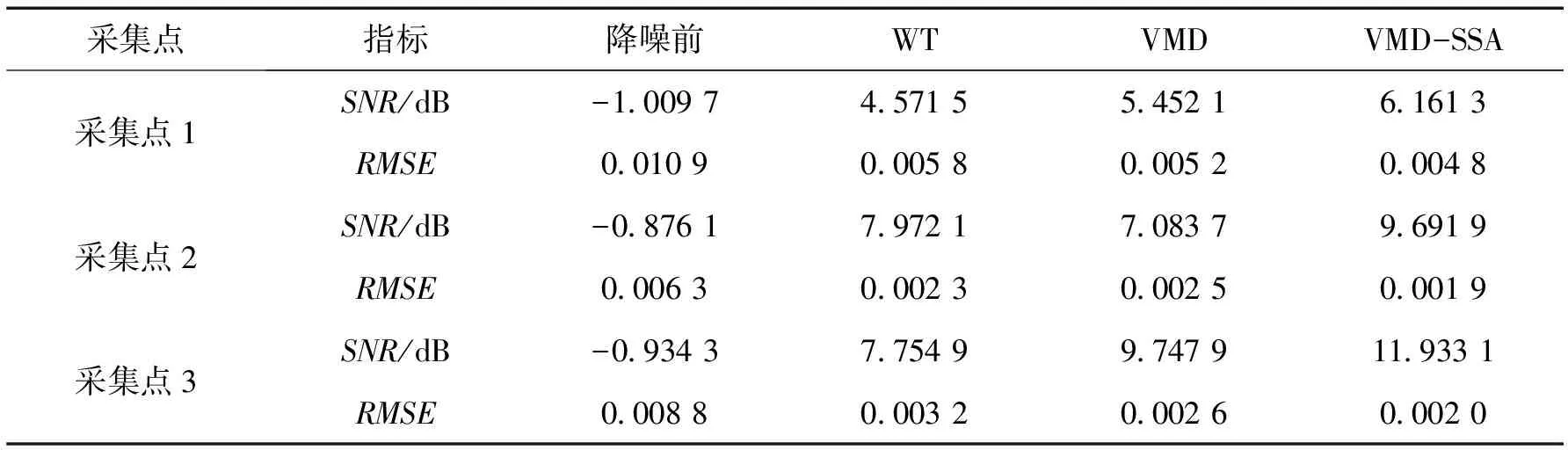
4.2 降噪性能指标
5 结 语
