计及故障距离的配电网单相接地有源消弧法

李 晖，张文海，陈坤燚，汪 颖，肖先勇

（1.四川能投发展股份有限公司，成都 611130；2.四川大学电气工程学院，成都 610065）

为提高供电可靠性，我国中压配电网主要采用小电流接地方式[1-2]，该类系统发生单相接地故障后，负荷供电不受影响，对于保障供电可靠性起到了重要作用，针对该类系统的故障选线和定位已进行了大量研究[3]。然而，当系统电容电流较大时，单相接地故障处产生电弧的熄灭和重燃容易导致系统过电压，危害系统安全[4]。因此，规定当系统电容电流大于10～30 A时，需采用中性点经消弧线圈接地[5]，消弧线圈通过提供感性无功分量用于补偿单相接地故障时的电容电流，减小故障电弧重燃机率。但消弧线圈消弧性能同时受调谐方式和电网对地电容的影响[6-9]，更重要的是消弧线圈的工作原理决定了其必然存在无法补偿故障电流中有功分量和谐波分量的问题，且随着电网规模的扩大和大量电力电子装置的接入，故障电流中的有功分量和谐波分量不断增加[10]，故障电弧抑制越来越困难。因此，研究可抑制含有功分量和谐波分量的单相接地故障消弧方法，具有重要理论价值和现实意义。

国内外对故障电流中有功分量和谐波分量抑制开展了大量研究，现有消弧方法可分为电流消弧法[2，11]和电压消弧法[10，12-15]，传统消弧线圈就是电流消弧法的典型代表，以补偿故障电流为目标。由于决定电弧是否熄灭的关键因素在于故障相电压和介质强度的相对恢复速度[12]，因此基于电压消弧成为了近年的研究热点[10，12-13]。现有电压消弧通常以将故障相母线处电压补偿等于0为目标，但是实际运行经验表明，由于故障点到母线间线路阻抗上必然存在电压降落，即使母线电压抑制到0，并不能保证故障点电压降为0。尤其对于农村中压配网，其线路较长，当故障点距离母线较远时，故障点残余电压较高，将引起较大残流，导致息弧失败，当馈线阻抗较大、负荷较重时，更加难以有效抑制故障电流[16]。

为了有效抑制故障点电压，必须考虑故障距离及负荷电流的影响，自适应调整逆变器参考电压。实际中，负荷阻抗可根据站端测量电压电流估计，但故障距离很难准确估计，因此，本文提出一种基于故障距离估计的配电网有源消弧方法。根据故障距离估计值计算逆变器参考电压，再由逆变器参考电压抑制故障电流，从而将熄弧后故障点恢复电压抑制到0。通过PSCAD/EMTDC仿真结果证明，本文方法的消弧效果好，能可靠地熄灭故障电弧，有效抑制配电网单相故障电弧。

1 消弧原理

假设某10 kV配电网如图1所示，中性点经逆变器接地。检测到单相接地故障后，逆变器从中性点注入电流，将故障电流抑制到0，促进电弧熄灭。电弧熄灭后，逆变器继续保持注入电流，将故障点电压抑制到0，防止电弧重燃。逆变器注入电流是有效抑制基波分量和谐波分量的关键。

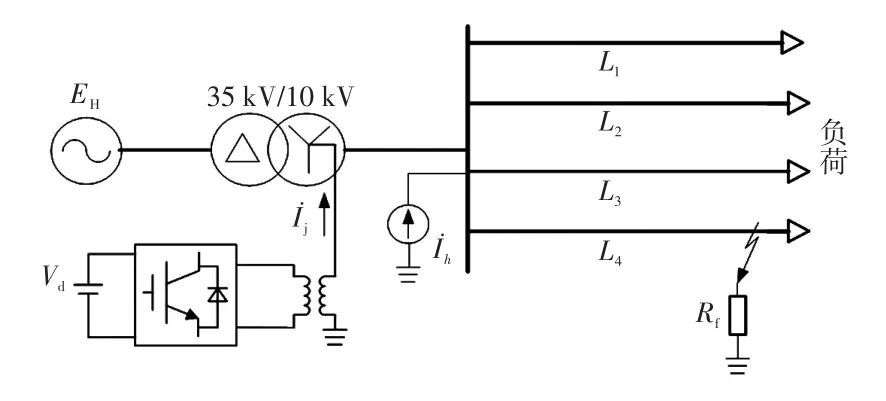
图1 带有有源消弧装置的配电网Fig.1 Distribution network with active device for arc suppression

1.1 基波电流和电压抑制原理

假设图1中线路L4发生单相接地故障，逆变器注入电流为̇j。根据对称分量法，图1所示配电网可等效为图2所示复合序网[17]。图2中，端口1-1′为故障点与大地构成的端口；ZS为系统阻抗（正、负序相同）；ZLf为故障线路正/负序阻抗；ZLD为非故障线路及其末端负荷阻抗的并联阻抗；ZLf0为故障线路零序阻抗；ZS0为系统对地零序阻抗；Rf为过渡电阻；α为故障点到母线的距离占故障线路总长度的百分比，称故障距离；Z′Df=ZDf+(1-α)ZLf，其中，ZDf为故障线路末端负荷阻抗；̇为故障相电源电压；̇、、分别为母线正序、负序、零序电压；̇f(0)为故障点的零序电流分量。

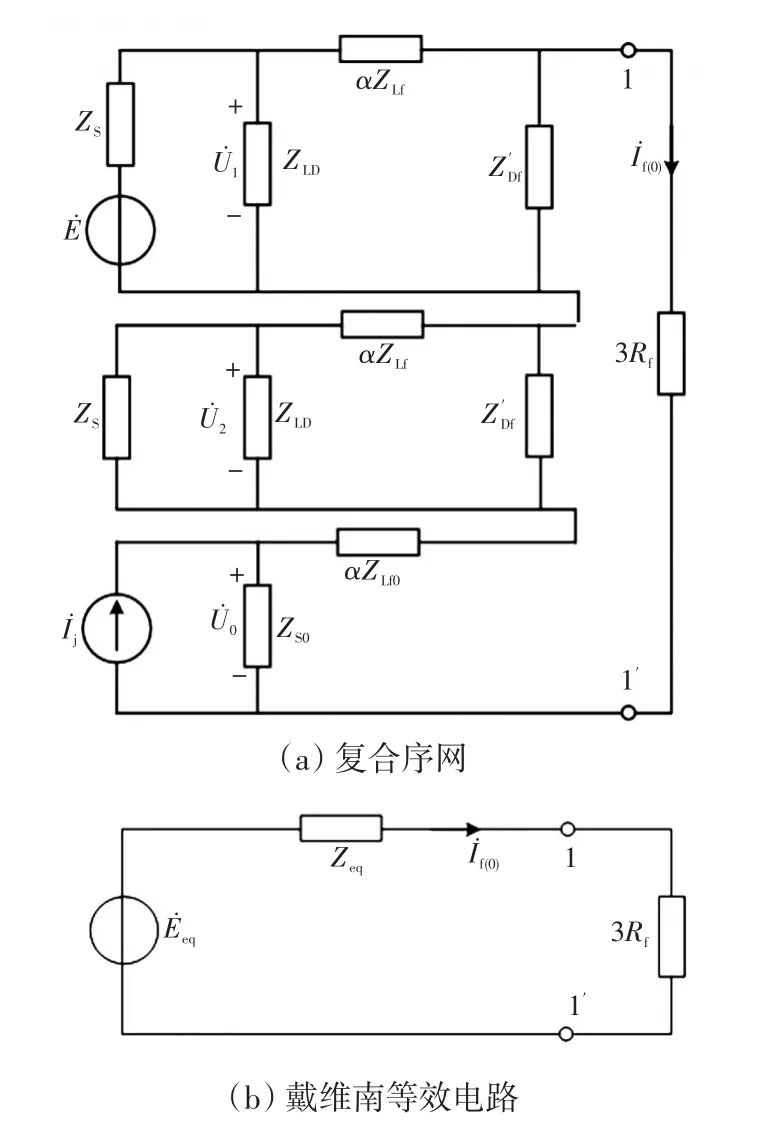
图2 复合序网及其戴维南等效电路Fig.2 Network with combined sequences and its equivalent Thevenin’s circuit

在图2（a）所示复合序网中，端口1-1′可用戴维南定理简化为图2（b）所示简化电路。其中，̇eq为戴维南等效电压，即故障端口开路电压；Zeq为戴维南等效阻抗。̇eq和Zeq可分别表示为

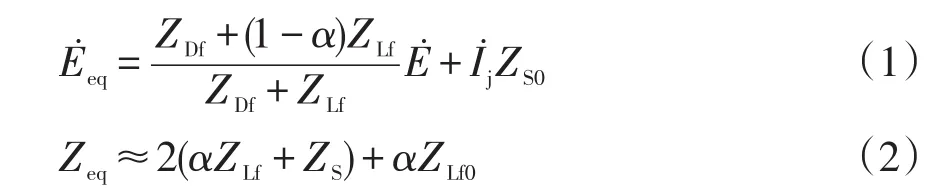
恢复电压定义为故障电弧熄灭后故障点电压。因熄弧后，弧道电阻非常大，可近似认为开路，恢复电压与戴维南等效电压近似相同。̇eq可通过调整逆变器注入电流进行控制，因此，令式（1）中̇eq=0，可得注入电流，即

对于母线电压控制法，逆变器工作后，逆变器输出电压被控制为 -̇，即̇jZS0=-̇，将其代入式（1）并结合式（4）可得

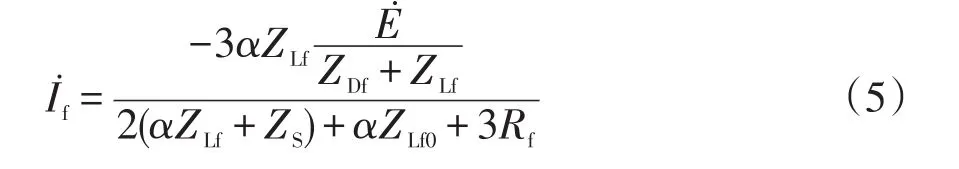
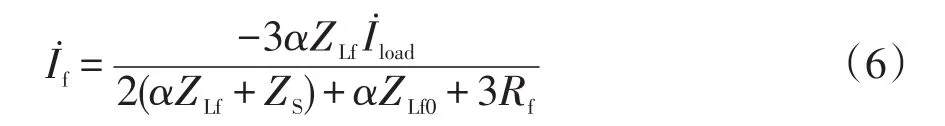
由式（6）可见，当线路非首端(α=1)发生接地故障时，若负荷电流较大，则母线电压控制法会存在较大的残余电流。过渡电阻可以减小残流，但过渡电阻具有一定随机性，不能依赖过渡电阻来减小残流。然而，若逆变器注入电流满足式（3），则̇eq=0，̇f=0。也就是说，只要按式（3）控制逆变器输出电流，就可将故障电流和恢复电压抑制到0，实现可靠消弧。不难发现，按式（3）对逆变器进行控制，需测量系统对地零序参数ZS0，但ZS0测量较复杂。同时，当式（3）满足时，流过ZS0的电流仅由逆变器决定。

可见，按式（7）控制逆变器输出电压可将故障点电流和恢复电压抑制到0。计算式（7）需已知故障馈线末端负荷阻抗和故障距离，下节将详细讨论。

1.2 谐波电流抑制原理

采用谐波源模拟法[7]，假设谐波电流源从一相接入，如图1中̇h所示。当电网单相接地时，仅考虑谐波源作用时，可得如图3所示的复合序网，其中，下标h表示谐波次数；Zh为逆变器h次谐波阻抗。

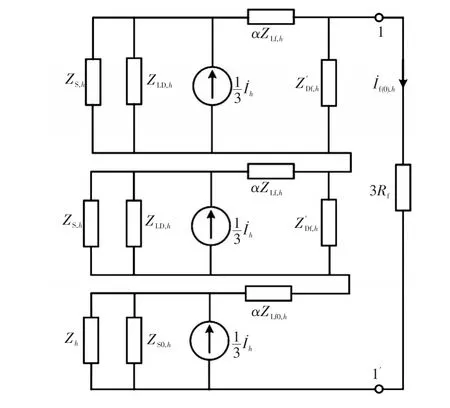
图3 谐波源作用时的复合序网Fig.3 Network with combined sequences when harmonic sources work

根据复合序网可得到逆变器投入前、后的故障支路谐波电流，即

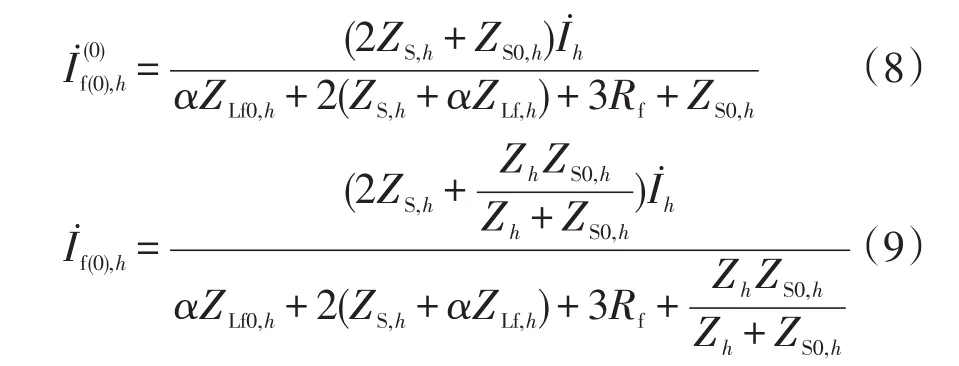
2 故障距离估计与消弧控制

当按式（7）计算逆变器参考电压时，需估计故障馈线末端负荷阻抗，并估计故障距离。

2.1 负荷阻抗测量

中性点非有效接地且发生配电网单相接地故障时，负荷不受影响，可继续运行2 h，因此，通过测量非故障相电气量可计算负荷阻抗。

由对称分量法可得

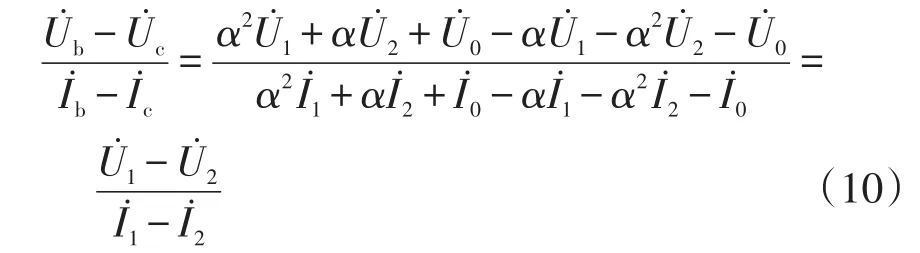
由图2（a）可知，母线正、负序电压为

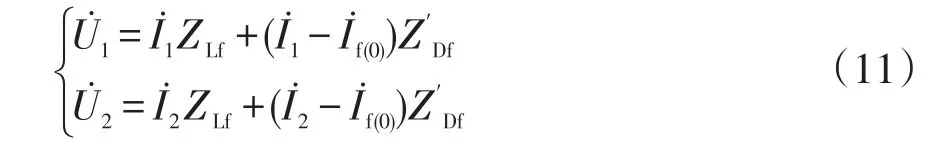
将式（11）代入式（10）可得

显然，根据式（12）可得到负荷阻抗。

2.2 故障距离估计

配电网故障直接精确测距较困难，本文采用间接估计法。假设估计故障距离为，根据式（7）计算逆变器参考电压。投入逆变器后，由于未准确获得故障距离，难以将故障电流抑制到0，此时故障电流为

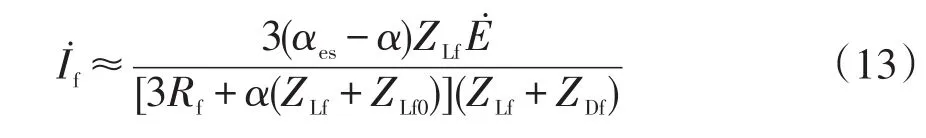
可见，投入逆变器后，故障电流与估计距离误差αes-α呈正比关系。因此，通过监测投入逆变器后的故障电流可判断估计距离的准确性。

为了判定估计故障距离的调整方向，可定义正方向矢量为

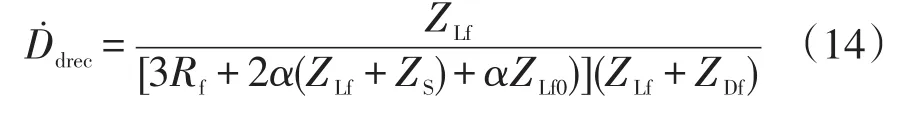
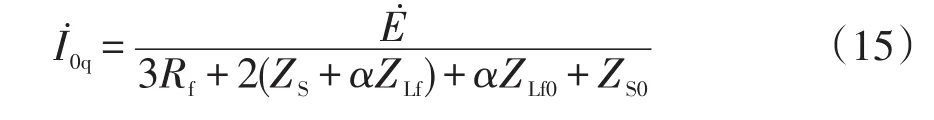
由式（15）可得过渡电阻为

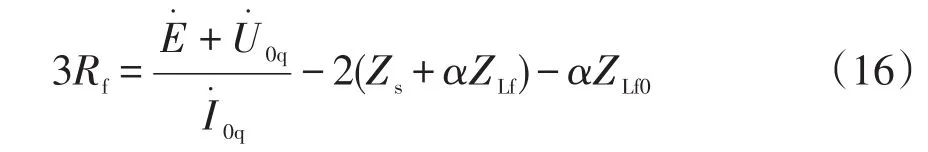
将式（16）代入式（14）可得

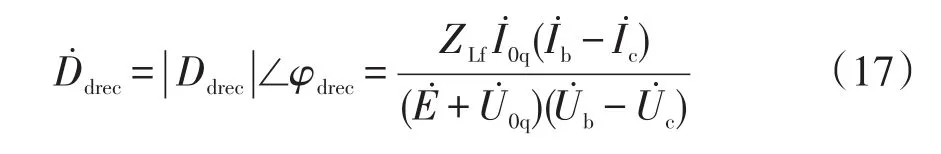
根据式（17）中故障电流与故障相电压间的相位关系可确定调整估计距离的方向。当与正方向相反时，增大估计故障距离；反之，减小估计故障距离。为了快速估计故障距离，采用二分法，每次估计距离为故障范围的一半，并按故障电流与故障相电压间的相位关系，调整估计范围，调整关系可表示为

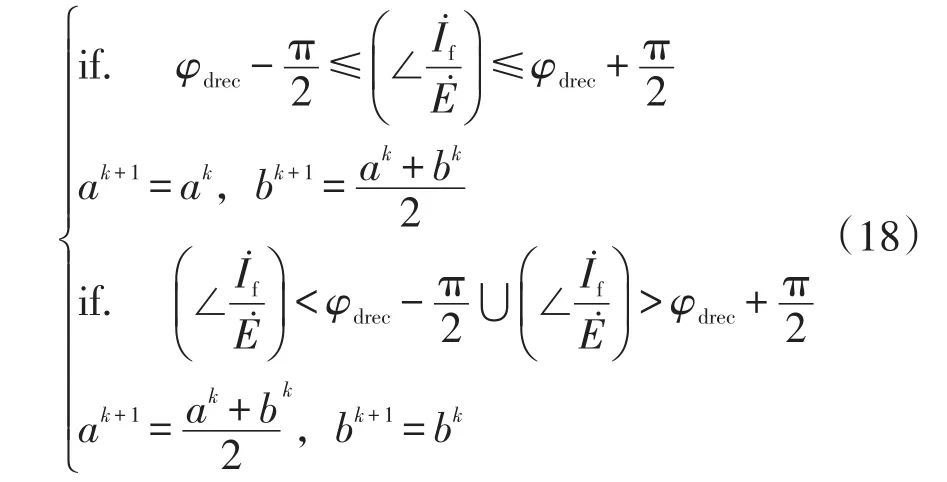
式中：ak为估计范围下界；bk为估计范围上界。

当故障电流与故障相电压相位关系与正方向相量相同时，可将估计范围上界调整为当前估计范围的一半；反之，将下界调整到当前估计范围的一半。根据故障电流量测值判断故障距离估计值的准确性，流程如图4所示，其中，ε为设定值，本文设定为1 A（对应实现故障电流小于3 A的目的）。需注意的是，这里的估计故障距离不是为了故障准确定位，不要求估计距离的精确度。

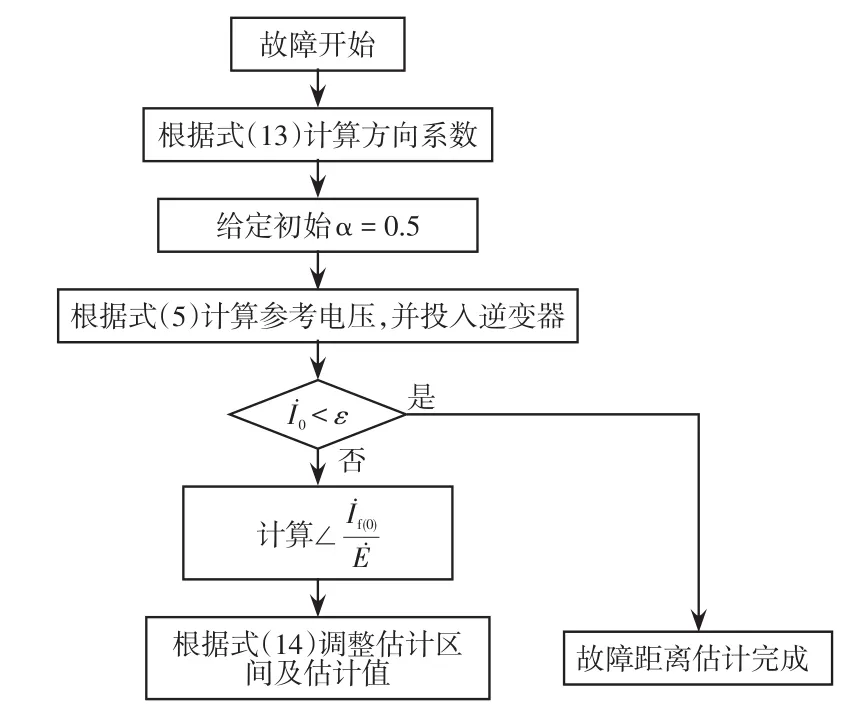
图4 故障距离估计流程Fig.4 Flow chart of fault distance estimation

2.3 逆变器控制策略

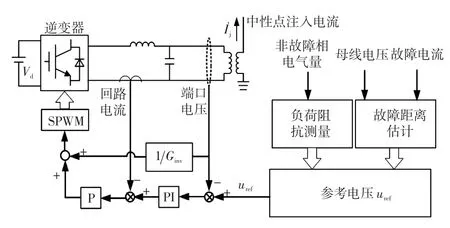
图5 逆变器控制逻辑框图Fig.5 Block diagram of inverter control logic

3 仿真验证

用PSCAD/EMTDC进行仿真，基于Matlab进行数据分析处理。电网模型如图1所示，在4条线路中，线路L1、L2为电缆，长度均为10 km，线路L3、L4为架空线路，长度分别7 km和10 km，线路阻抗如表1所示。L1和L2的负荷均为1.4 MV·A，L3的负荷为1.0 MV·A，L4的负荷为3.4 MV·A，4条线路的负荷功率因数均为0.9。中性点逆变器及其控制系统参数如表2所示。考虑仿真谐波的影响，接入5次和7次谐波电流，幅值均为10 A。为了与消弧线圈比较，配置脱谐度1%的过补偿消弧线圈，线圈电感为0.624 7 H，电阻为19 Ω。

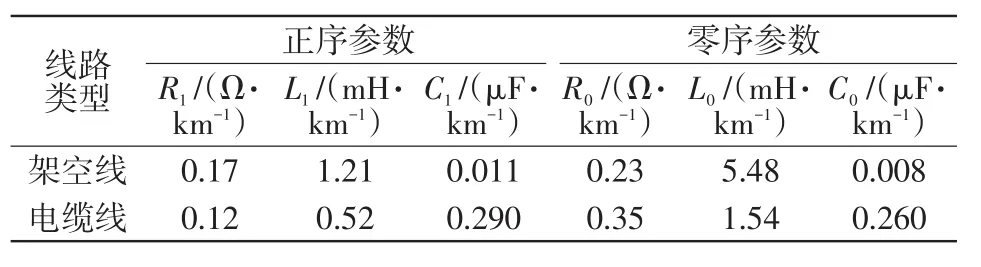
表1 仿真模型线路阻抗参数Tab.1 Line impedance parameters of simulation model

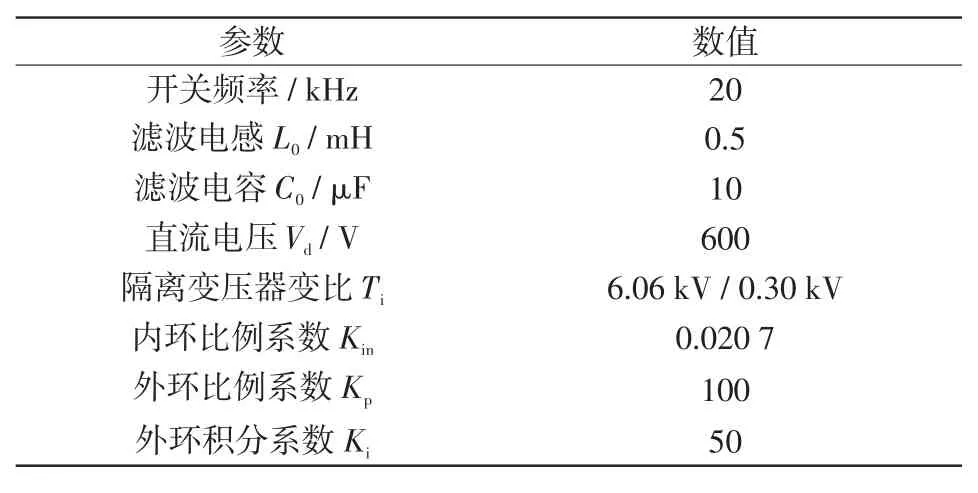
表2 逆变器及其控制系统参数Tab.2 Inverter and the parameters of its control system

3.1 电流抑制能力仿真验证

假设单相接地故障发生在馈线L4的c相上，过渡电阻设置为30 Ω。电流和母线电压的仿真波形如图6所示。图6中，故障发生在0.1 s，基波故障电流为31.00 A，5次谐波电流为9.80 A，7次谐波电流为5.30 A。为了更好地对比投入消弧装置前后的补偿效果，延迟0.2 s投入消弧装置，在0.3 s时有源消弧装置开始工作，基波电流降低到了2.26 A，5次和7次谐波电流基本降低到0。可见，本文提出的消弧方法可有效抑制故障电流。

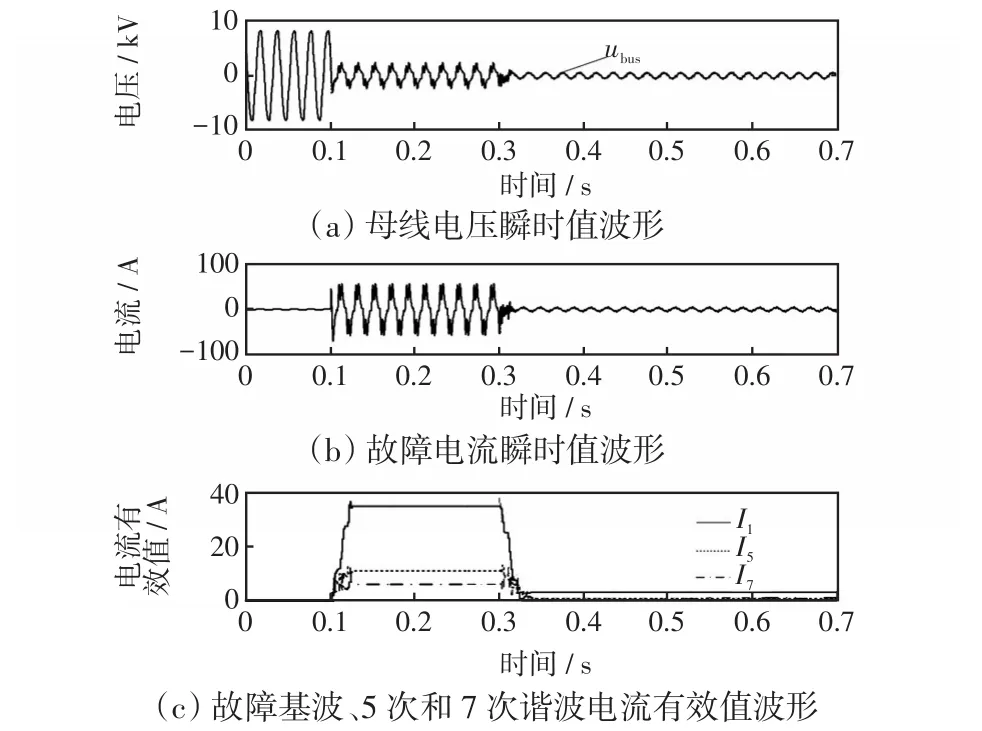
图6 母线电压和故障电流波形Fig.6 Waveforms of bus voltage and fault current

本文提出的消弧方法与消弧线圈、母线电压控制法抑制故障电流的性能比较如表3所示。可见，本文基于故障距离估计的有源消弧法能有效地将故障电流减小至设定值（3.00 A）以下。然而，对于母线电压控制法，故障距离位于线路末端，当过渡电阻为30 Ω时，补偿后残流为24.81 A；当过渡电阻为50 Ω时，残流为15.97 A；当过渡电阻为100 Ω时，残流为8.42 A。可见，随着过渡电阻的增大，补偿后的残流在逐渐减小，但是即使过渡电阻达到100 Ω，残流也相当可观，这是由于故障线路的负荷较大造成的。由此可见，母线电压控制法很难保证可靠地减小故障电流，无法有效熄灭电弧。另外，由表3中谐波电流数据可知，本文提出的方法和母线电压控制法对谐波电流均有较好的抑制效果。消弧线圈能减小基波故障电流，但不能有效抑制故障谐波电流，当在过渡电阻较小时，谐波电流较大。

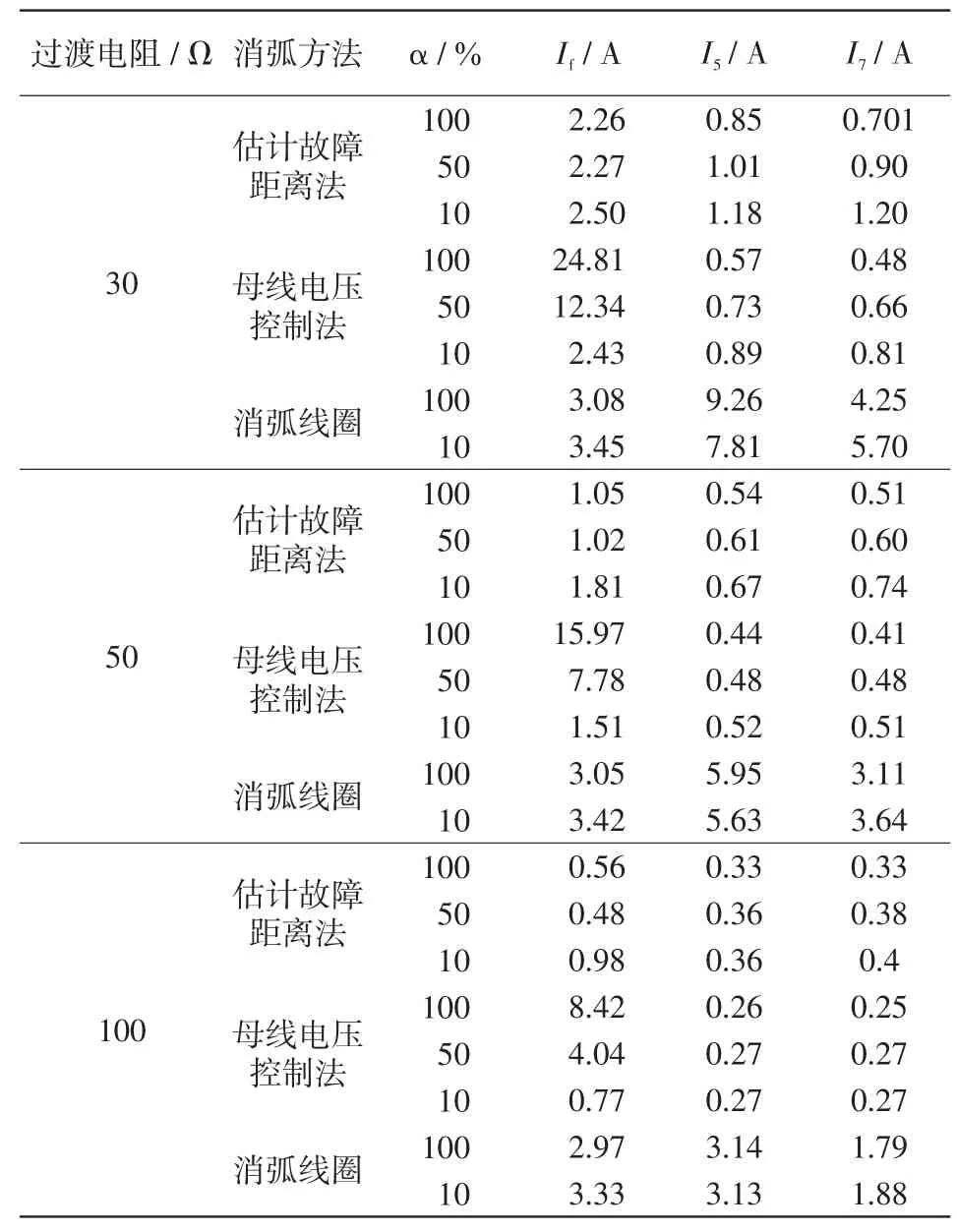
表3 不同消弧方法电流抑制性能比较Tab.3 Comparison of performance among several arc-suppression methods

3.2 故障距离与负荷阻抗测量方法仿真验证

为了验证故障距离估计方法的可行性和负荷阻抗测量方法的正确性，针对不同情况进行了仿真，结果如表4所示，其中，ZDf_real为真实负荷阻抗，ZDf_m为测量负荷阻抗。可见，本文方法能准确计算负荷阻抗；对于故障距离估计，当过渡电阻较小时，误差相对较小，当过渡电阻较大时，误差较大，但故障电流均可以有效抑制，说明本文方法不要求故障距离的准确估计也能有效抑制故障电流，证明了本文方法的正确性。

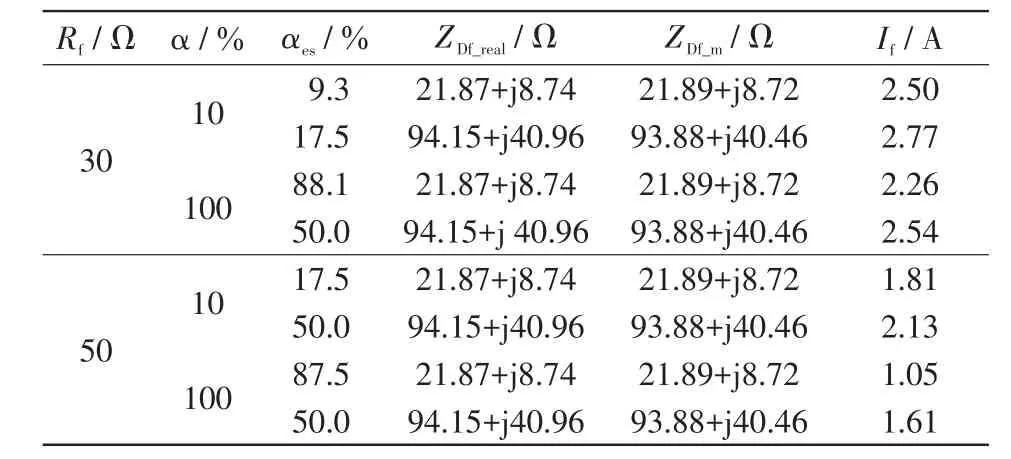
表4 故障距离估计和负荷阻抗测量结果Tab.4 Results of fault location estimation and load impedance measurement

3.3 恢复电压抑制性能仿真验证

假设单相接地发生在L4末端，过渡电阻为100 Ω。电弧熄灭过程用断路器模拟，仿真结果如图7所示。图7中，曲线A为消弧线圈工作时故障点恢复电压，曲线B为本文提出的基于故障距离估计的抑制方法下的恢复电压，曲线C为母线电压抑制法工作时的恢复电压。t=0.1 s时故障发生，在t=0.4 s电流过零时故障清除。由图7（a）可见，3种情况下，故障清除瞬间故障点电压均可抑制到很低值，但曲线B和C可一直保持，曲线A振荡恢复到额定电压。可见，有源消弧法的抑制性能比消弧线圈好。

由图7（b）可见，曲线B的恢复电压瞬时值一直低于0.16 kV；t=0.403 4 s时曲线C的恢复电压超过了1 kV，耗时3.2 ms，最大电压值1.194 kV；曲线A恢复电压超过1 kV，耗时2.2 ms。显然，本文方法的恢复电压抑制效果更好，有利于阻止电弧重燃。

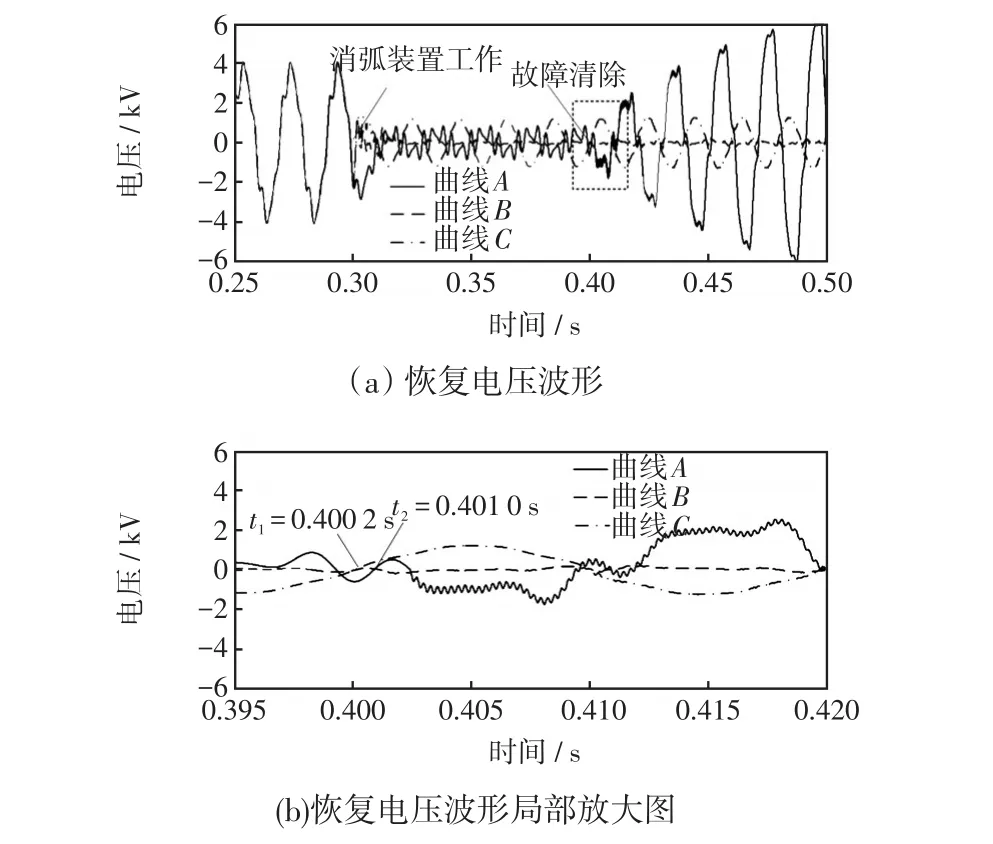
图7 故障点恢复电压波形Fig.7 Waveforms of recovery voltage at fault point

4 结语

综上，当计及故障线路上电压降落时，传统有源消弧法受负荷影响存在消弧困难的问题。本文提出的基于故障距离估计的有源消弧方法，采用二分法估计故障距离，由此计算合适的参考电压，通过逆变器跟踪参考电压的方式可将故障电流和恢复电压抑制到0，有效提高了消弧可靠性。PSCAD/EMTDC仿真验证了本文方法的可行性，与同类方法比较，本文方法能将故障电流和恢复电压有效抑制到较低值，具有更好的消弧效果。在未来研究中，将进一步讨论其工程实现方法。