风电接入对电力系统小干扰稳定影响分析方法

2021-10-22姜惠兰白玉苓王绍辉

电力系统及其自动化学报 2021年9期

姜惠兰，白玉苓，王绍辉，肖瑞

（智能电网教育部重点实验室（天津大学），天津 300072）

风力发电作为解决当前环境恶化和能源问题的重要途径，在世界范围内迅速发展，但风电并网会对系统的小干扰稳定造成很大影响，因此有必要研究风电场接入对系统的小干扰稳定的影响[1-2]。

目前国内外学者在此方面已取得一定的成果。常用的分析电力系统小干扰稳定性方法是阻尼转矩法和特征根分析法。阻尼转矩分析方法推导较复杂，常用于分析单机无穷大系统。故对于多机电力系统普遍采用特征根分析法。

文献[3-9]利用特征根分析法研究双馈风机DFIG（doubly-fed induction generator）接入对系统小干扰的影响。文献[3]建立了风机的小干扰数学模型，仿真结果表明系统中引入了与风电场强相关的振荡模式，且风电比例增加降低对外网阻尼特性。文献[4]推导了含风电场的电力系统小干扰稳定的状态矩阵，并通过算例仿真发现风电接入不参与系统原有的机电振荡模式。文献[5]利用四机两区域系统仿真研究了风电出力、调度方式及机端电压控制参数对系统小干扰稳定的影响。文献[6]通过四机两区域系统仿真研究了调速器、DFIG电阻及不同工况下DFIG和系统的动态交互行为。文献[7-8]主要研究了风电渗透率的变化对系统小干扰稳定的影响。文献[7]研究了DFIG工作在不同风速运行模式下，电力系统振荡的模态和阻尼随风电渗透率的变化情况。文献[8]通过算例仿真表明当风电渗透率增加到50%以上时会对系统的阻尼产生负面影响。但上述文献大多是通过建立包括DFIG在内的全系统小干扰稳定模型，然后针对具体算例分析包含风电的系统小干扰稳定性，并没有考虑到DFIG特殊的机电解耦特性，不能从理论上说明DFIG和系统的关联关系，同时系统状态矩阵的维数较大，容易造成维数灾问题。文献[9]建立了DFIG与1台同步电动机相连的简化系统，研究表明DFIG接入系统是通过改变系统稳定平衡点来影响其小干扰稳定性，但没有从风电场的实际接入位置入手，所得结论的普适性有待商榷。

本文通过风电场接入后对系统节点电压方程的修正和收缩处理，将风电场接入系统的位置信息和输出特性反映到系统同步机之间的电气联系中，使风电场对系统的影响量化为对同步机电磁功率的改变，并将其映射到系统状态矩阵的改变，进而将风机接入与系统的小干扰稳定性联系起来。采用这种方式可以更为直观地反映DFIG与系统的关联关系，降低了分析整个系统状态矩阵的复杂性，为风电场接入对系统小干扰稳定性影响的量化分析提供了途径。

1 DFIG影响系统功角稳定性的途径

电力系统的小干扰稳定性是指当系统受到小的扰动后，不发生自发振荡或者非周期性失步，能自动恢复到起始运行状态的能力。对于传统的机电暂态过程，当系统遭受扰动后，同步机的电磁功率受到影响，并通过“电磁功率-功角”特性影响各同步机的功角，从而引发同步机转子角振荡，出现同步机功角的互同步稳定问题。但由于DFIG具有双变流器结构与矢量控制，其输出的电磁功率和自身的转子运动特性没有必然联系[10]，所以DFIG主要是通过输出功率特性影响同步机的运行特性，进而影响系统的小干扰稳定性。

小干扰稳定的研究目标是系统的同步稳定性，而DFIG的机械运动和功率特性没有必然联系，所以DFIG自身的转子运动不是同步稳定性研究的部分，可将DFIG作为1个非自治因素，研究其向系统输入的有功和无功功率。为分析方便，本文将DFIG的输出功率特性用等效接地导纳模型来代替，即

式中：Pdfig和Qdfig分别为DFIG输出的有功功率和无功功率；Udfig为并网点电压。

2 不含风电场时系统的状态方程

设发电机组均为经典二阶模型，发电机暂态电抗Xd′后的暂态电动势E′及机械功率Pm均恒定，考虑系统经受小扰动，多机系统转子运动方程在工作点附近线性化，可得到如下矩阵形式的增量方程：

本文通过理论推导风电输出功率与系统各同步机电磁功率的关联关系，使风机接入对系统自身的小干扰稳定性的影响分析得以量化。

3 DFIG接入对同步机电磁功率的影响

将系统中的所有节点分为3类：发电机的内电势节点S、DFIG并网节点W、其余普通功率交换节点R。由于发电机的电磁功率表达式与系统的网络参数、各发电机的内电势电压和功角有关，需要对系统节点电压方程等效变换，将系统各节点收缩至发电机内电势节点。根据节点分类得到系统节点电压方程，即

式中：YSS、YWW、YRR分别为节点S、节点W、节点R的自导纳；YWS、YSW分别为节点W和节点S之间的互导纳；YSR、YRS分别为节点S和节点R之间的互导纳；YRW、YWR分别为节点R和节点W之间的互导纳；̇S为同步机内电势；̇W为DFIG并网节点电压；̇R为普通节点电压；̇W为DFIG并网节点注入电流；̇S为同步机节点注入电流。

通过收缩普通节点R，得到同步机内电势节点和DFIG并网节点的电气联系，即

其中

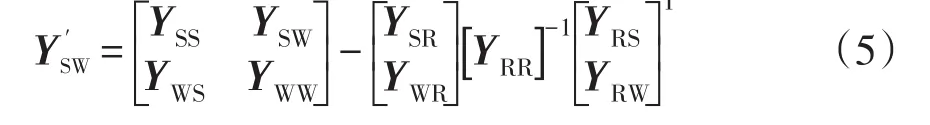
式中，Y′WW0为收缩节点R后节点W的自导纳。

DFIG并网点W处用等效导纳表示后，需要修正式（4）。由于W节点不再具备功率源特性，故W节点的注入电流̇W应为0。DFIG等效接地导纳影响了W节点的自导纳，故Y′WW0应修正为Y′WW=Y′WW0+ydfig，即

对式（6）进行进一步收缩可得

其中

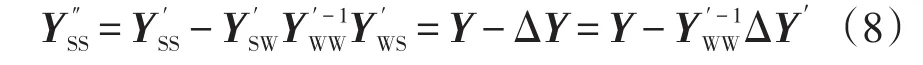
式中，Y和ΔY分别表示仅含有同步机系统收缩后的节点导纳矩阵和DFIG接入后的修正量。

令

式中：Gij、Bij分别为仅含有同步机系统收缩后的同步机之间的电导、电纳；ΔGij、ΔBij分别为DFIG接入后系统同步机之间电导、电纳的改变量；ΔG′ij、ΔB′ij分别为DFIG接入后系统除去节点W自导纳的同步机之间电导、电纳的改变量。

这样可将DFIG输出功率信息转移到对同步机间电气距离的影响上，从而计算得到同步机i电磁功率 Pei，即

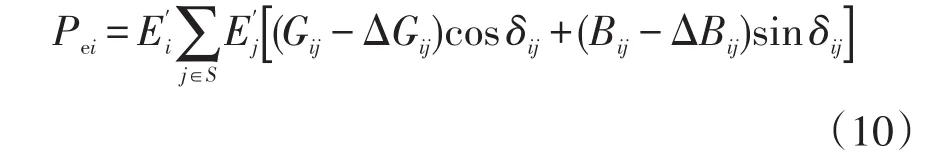
式中：E′i为第i台同步机内电势；δij为同步机i、j之间的相对角，δij=δi-δj，其中 δi为第i台同步机的功角；S为节点S的集合。

4 含DFIG时系统的小干扰稳定特性

为了简化说明，本文以图1所示的含DFIG的两机系统为例进行分析。从DFIG的实际接入位置入手，利用第3节的收缩方法求出DFIG接入系统后对各台同步机电磁功率的量化影响，进一步将这种影响映射到DFIG对系统小干扰稳定的影响。

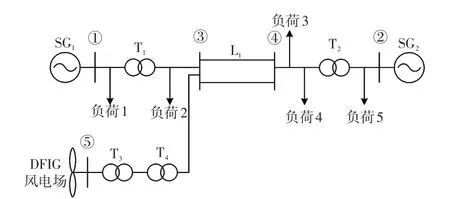
图1 含DFIG的两机系统Fig.1 Two-machine system with DFIG

从功率特性方面来看，DFIG的接入改变了同步机的自导纳和互导纳，由式（10）可知，同步机的电磁功率特性发生变化，即图2所示的两机系统功角特性曲线中的虚线变为实线，电磁功率特性曲线和机械功率特性曲线的交点为同步机1、2的相对功角初值δ120，所以δ120的相对位置发生了变化，即系统平衡点的位置发生了变化。相对功角稳态初值为

图2 两机系统的功角特性曲线Fig.2 Power-angle curves of two-machine system

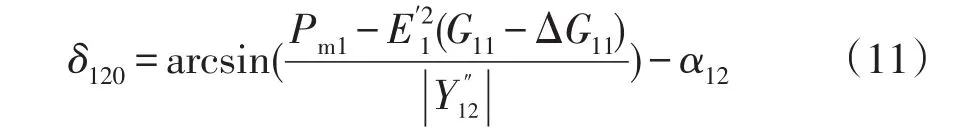
式中：α12为收缩后同步机1、2之间的互阻抗Y″12的阻抗角；Pm1为同步机1的机械功率。

由于同步机1、2的暂态电动势恒定，取E′1=E′2=1，因在扰动过程中风电的有功影响远大于无功影响[11]，下面推导中仅考虑DFIG有功输出，即ydfig=-Pdfig/U2dfig。为表述方便，令Y′WW=(G0+ydfig+jB0)，对式（10）在平衡点处进行线性化，即

其中

式中：SE1和SE2分别为同步机1、2的同步转矩系数；下标0表示平衡点初值；1、2分别为同步机1、2的功角增量。

根据文献[11]，由有功功率微变引起的电压微变较小，可忽略不计，即ΔUdfig=0，而DFIG输出的有功功率变化量可以表示为dfig=gB，其中g为DFIG的动态频率特性模值，B为DFIG并网点的频率变化量。送电侧和受电侧的频率微变均可用相应侧的发电机转速表示。以DFIG接入送电侧为例，B=α11，α1为正系数，1为同步机1的转速增量，设dfig=gα11=β11，式（12）可简化为

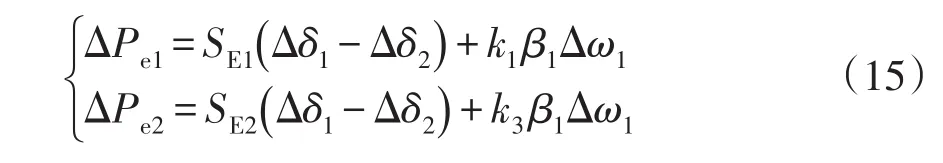
式中，β1为系数，β1=gα1。

式（15）表明DFIG的接入主要是从两个方面影响系统的小干扰稳定性：①DFIG接入改变了系统的平衡点及各同步机之间的电气联系，主要影响了同步机的同步转矩系数SE1和SE2；②系统发生小扰动的动态过程中，DFIG出力变化参与了系统的振荡，改变了同步机的阻尼系数，阻尼特性越好，系统抑制振荡的能力越强。

将式（15）代入到式（2）得到含风机的双机系统的状态方程矩阵形式，即

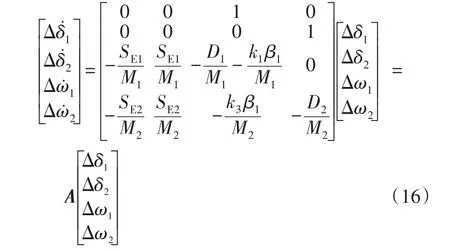
式中：D1、D2分别为同步机1、2的阻尼力矩系数；M1、M2分别为同步机1、2的转子惯性时间常数；A为状态方程的系数矩阵。

根据李雅普诺夫第一定律，非线性系统的小干扰稳定性是由矩阵A的特征值所确定的。根据矩阵对角元素之和为该矩阵特征值之和，矩阵A对角线元素之和为系统阻尼之和。可以看出，DFIG接入后系统总阻尼改变量为-k1β1/M1，当k1β1为正值时，DFIG为系统提供正阻尼，有利于系统小干扰稳定；反之，DFIG为系统提供负阻尼，不利于系统小干扰稳定。另外，同步转矩系数改变也会使各振荡模式的阻尼分配发生变化。

下面针对DFIG接入改变系统初始平衡点及电气距离方面，分析DFIG接入对反映系统小干扰稳定性的振荡模式的影响关系。令 β1=0，根据|λE-A|=0，通过矩阵变换可得

式中，λ为特征值。

假设同步机符合均匀阻尼的条件[12]，即D1/M1=D2/M2=γ，则式（17）简化为

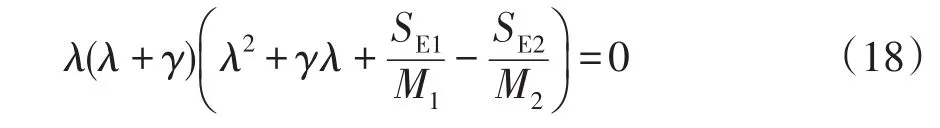
进而求得系统特征方程的根为

可以看出，零根λ1不反映系统的稳定性特征[13]。当系统正常运行时阻尼D为正值，故λ2为负实数，因此系统的稳定性主要决定于λ3,4。DFIG接入影响了SE1和SE2，定义K=SE1/M1-SE2/M2，K中包含了DFIG的输出特性及系统初始平衡点等信息。由式（17）可知，系统稳定的判定条件是K>0。当0<4K<(D1M1)2时，λ3,4为两个负实根；当4K>(D1M1)2时，λ3,4为一对实部为负的共轭复根，K越大，系统振荡频率越大，振荡阻尼比越小。通过以上推导将DFIG接入对系统小干扰稳定性的影响量化到对系统原有振荡模式的改变。

5 算例分析

5.1 两机系统仿真

为验证含有DFIG的电力系统小干扰稳定性分析方法的正确性，在Matlab/Simulink平台中搭建了如图1所示的含有双馈风电场的两机系统仿真模型。其中，负荷采用恒阻抗模型，同步发电机SG1和SG2的额定功率分别为100 MW和200 MW，单台DFIG额定功率为1.5 MW，风电场中DFIG台数根据风电接入容量而变化。分析大型风电场对电网动态稳定影响主要采用的等值动态模型分为单机等值法和多机等值法[14]。本文选用了最常用的单机等值法，将风电场所有的DFIG等值为1台。另外，风电场出力百分比是在总负荷不变的情况下，风电场替代SG1出力的比例。

5.1.1 理论分析

在本算例中，DFIG正常运行时采用恒功率因数控制，与电网不存在无功功率交换。表1展示了风电场不同出力时等效导纳数值及相对功角初始值 δ120。

表1 风电场不同出力情况下系统初值Tab.1 Initial value of system under different wind farm output

将算例参数代入节点电压方程，然后收缩至发电机内电势节点，进一步根据式（16）计算出风电不同出力情况下系统的机电振荡模式如表2所示。

表2 两机系统机电振荡模式Tab.2 Electromechanical oscillation mode of two-machine system

由表2可知，所有特征值实部为负数，该系统稳定，进一步发现随风电接入比例的增加，振荡频率呈减小趋势，阻尼比呈增大趋势，系统小干扰稳定性增强。这种现象出现的原因主要包括以下两方面。

（1）风电场出力不同影响了系统总阻尼增量。随着风电输出功率增加，风电有功变化量dfig增大，因而 β1增大，同时同步机1、2间的相对功角δ120减小，且改变了同步机的自导纳和互导纳。由式（14）可知，k1是非线性变化的。本算例的总阻尼增量(-k1β1)为负值，系统阻尼增加，有利于系统小干扰稳定。

（2）根据同步机功角特性曲线，对于稳定运行区域，DFIG接入后同步机有功出力减少，同时由式（10）计算得出的电磁功率增大，静态稳定储备系数增加，增强了系统的小干扰稳定性。

5.1.2 仿真验证

本文仿真分析了DFIG接入前后对系统动态响应的影响。假设当t=0.1 s时节点4处发生三相短路故障，t=0.2 s时切除。在风电场不同出力百分比下SG1和SG2相对功角及SG1有功功率曲线如图3所示。从相对功角曲线可以看出，风电场接入系统后，同步机组的相对功角的初始值降低，振荡幅度减小，恢复稳定的时间减小，系统的阻尼特性变好。同样，SG1有功功率曲线和δ12变化规律基本一致，系统稳定性增强，仿真结果与理论分析结果一致。

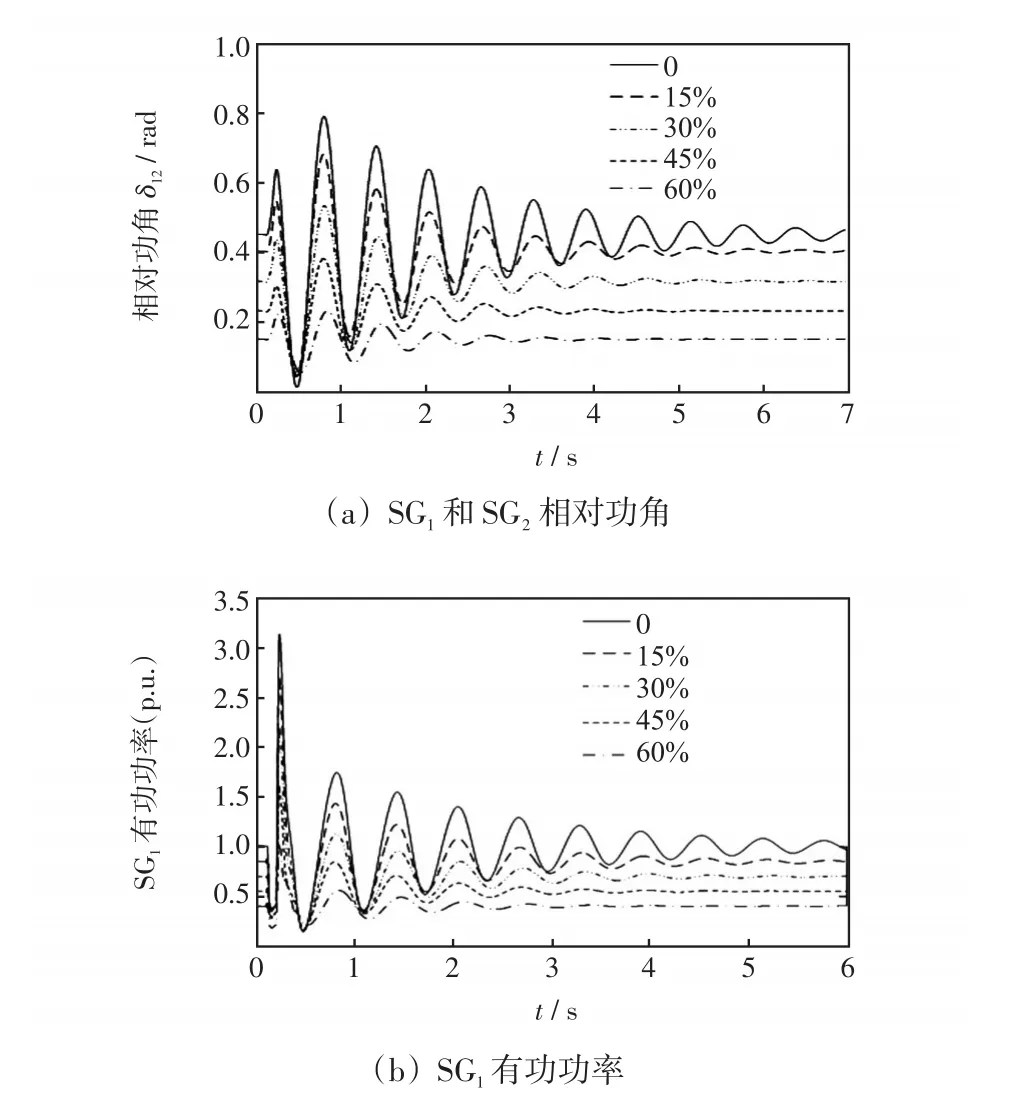
图3 两机系统动态响应曲线Fig.3 Dynamic response curves of two-machine system

5.2 多机系统仿真

5.2.1 理论分析

为进一步验证本文所提方法在多机系统中的适用性，对图4所示的含有DFIG的三机九节点系统进行仿真分析。SG1、SG2和SG3的额定容量分别为248 MW、192 MW和128 MW。风电场接入节点5，当风电场出力增加时，减少SG2的出力以维持功率平衡。

图4 含DFIG的三机九节点系统结构Fig.4 Structure of three-machine nine-node system with DFIG

在不同出力情况下三机系统的机电振荡模式如表3所示，图5为两个振荡模式的变化过程。可以看出，系统中包括两个机电振荡模式：振荡模式1随着风电出力的增加，其阻尼比呈现先增加后减小的趋势，但总体变化程度不是很大；振荡模式2随风电出力增加阻尼比单调增大。

表3 三机系统机电振荡模式Tab.3 Electromechanical oscillation mode of three-machine system

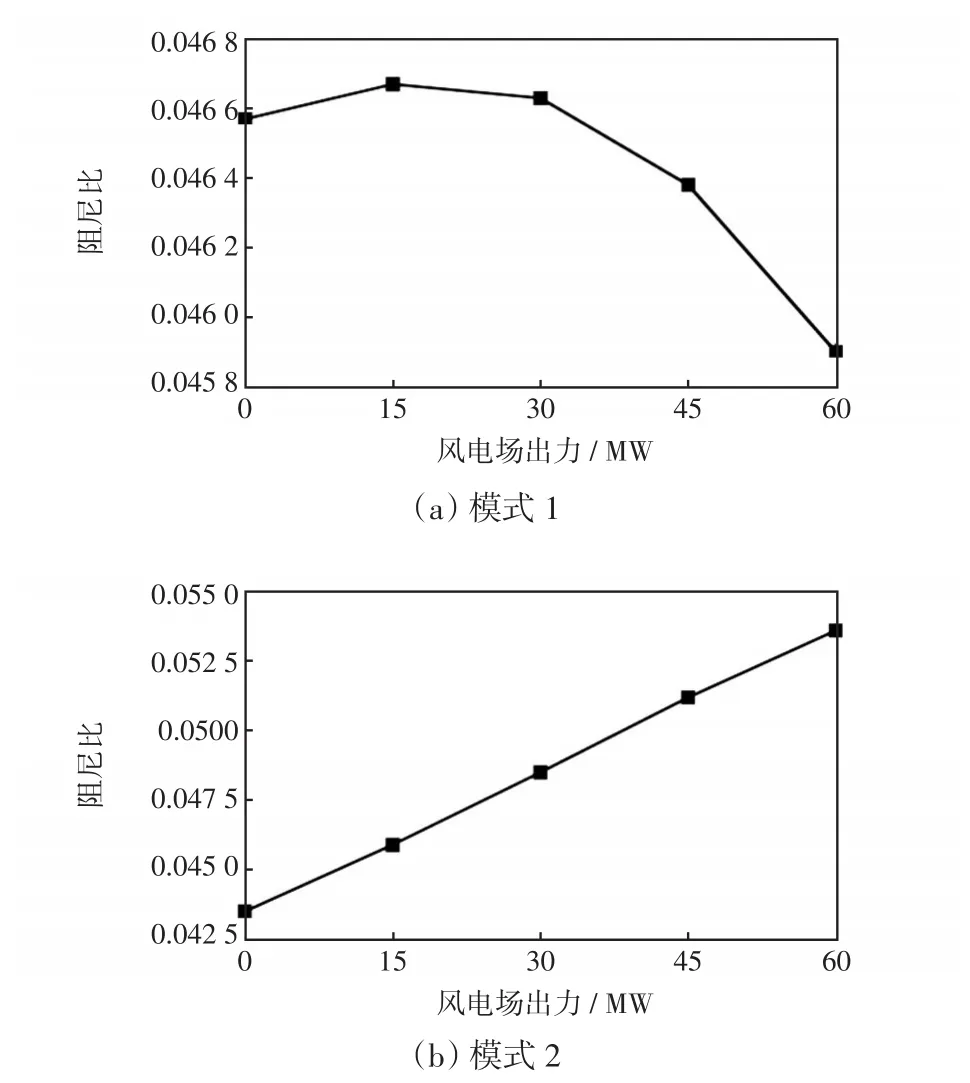
图5 模式1和模式2的阻尼比变化Fig.5 Changes in damping ratio in modes 1 and 2

影响上述振荡模式变化的因素主要包括3个方面：①风电出力增加时，对系统平衡点、同步机之间电气距离以及风电与系统的动态交互作用影响不同，系统阻尼增量呈非线性变化；②SG2出力减少，功角减小，静态稳定储备系数增大，同步运行能力增强，有利于系统稳定；③在SG2和SG3之间联络线具有相同交换功率的前提下，风电占比增加，系统的阻尼比增强[15]。对于每种振荡模式来说，上述因素影响程度不同，造成每个振荡模式的变化趋势不同。

5.2.2 仿真验证

假设在t=0.1 s节点8处发生三相短路故障，t=0.3 s时切除，不同风电出力时系统的动态响应如图6所示，其中不同线型表示0～60 MW风电出力。图6（a）中SG2和SG1的相对功角δ21曲线显示随着风电场出力的增加，δ21首摆幅值越来越小，恢复到稳定状态的时间越来越短，但当出力达到45 MW和60 MW时，两条曲线相差不大。图6（b）中SG2的有功输出与δ21趋势基本一致。对于图6（c）中SG3的有功输出，当风电接入达到60 MW时，振荡幅度和恢复稳定的时间都略高于风电接入45 MW时的情况，说明阻尼有所降低，所以需要合理配置风电接入比例，避免系统阻尼特性降低过多而影响系统安全运行。仿真结果与理论计算结果较为吻合。