心墙曲率对坝体应力位移特征影响的数值模拟研究

杨东玲

（凌源市节约用水管理办公室，辽宁凌源 122500）

1 研究背景

拟建中的双龙水电站属于辽宁省东部半拉江梯级开发的重要水利工程，坝址位于高龙泡水电站下游太平哨镇二龙渡村境内，属于典型的河床式水电站设计[1]。电站大坝为沥青混凝土心墙土石坝坝型，最大坝高56.0m，坝顶高程160.0m，坝顶宽8.0m。大坝按照百年一遇洪水标准设计，千年一遇洪水校核，水库的正常蓄水位为157.50m，校核水位为158.50m。

沥青混凝土心墙土石坝作为一种新坝型，可以充分发挥沥青混凝土的良好抗渗性，是一种具有良好适应性和发展前景的坝型[2]。从当前的工程现状来看，沥青混凝土心墙的防渗效果良好，极少发生渗透破坏，可以充分保证土石坝的安全稳定。另一方面，沥青混凝土心墙还具有较好的变形适应性，在大坝发生变形的情况下可以作出适应性改变，抗震性能十分优异[3]。迄今为止，我国已经建成的沥青混凝土心墙土石坝，均运行良好，并没有发生渗透破坏性事故[4]。对于传统的直心墙坝型，在建成运行期间，心墙受到上游水荷载的作用，会产生向下游的变形，进而在坝肩部位产生一定的拉应力。如果坝体的高度较大，上述拉应力值也会明显偏大，一旦超过心墙材料的抗拉强度，就可能造成破坏[5]。因此，对于高混凝土心墙土石坝，往往采取曲心墙设计。下文以拟建中的双龙水电站大坝为例，利用数值模拟的方法展开心墙曲率对坝体应力位移特征影响研究，以期为相关工程设计提供必要的理论借鉴。

2 有限元计算模型的构建

2.1 计算模型的建立

ANSYS软件是一款大型通用三维有限元模拟软件，具有十分完善和强大的数值模拟功能，在工程研究和设计领域具有十分广泛的应用。该软件的一个重要特点就是，可以在建模计算过程中直接和CAD软件进行数据交换，可以根据工程模拟计算的需要，对已经构建的模型进行必要的调整，从而通过网格划分的优化，提高模拟计算的效果和质量[6]。基于此，此次研究选择ANSYS软件进行研究对象的模型构建。

此次研究以背景工程特点为依据选择模拟计算的范围，不仅包括双龙水电站的大坝主体，还涵盖了两侧的部分山体，模型长350.0m、宽150.0m、高75.0m。在模型构建过程中，坝轴线指向右岸的方向为Y轴正方向，以垂直于Y轴指向下游的方向为X轴正方向；以竖直向上的方向为Z轴正方向[7]。利用六面体等参单元进行几何模型的网格划分，并对心墙等关键部位进行必要的加密处理，整个模型划分为65465个计算单元，89787个计算节点。

2.2 计算参数和边界条件

结合研究的具体需要，选择邓肯模型为模型的本构模型[8]。模型的计算参数对模拟计算结果存在显著的影响，因此研究中以相关规范为基础，结合现场采样试验数据，确定如表1所示的计算参数。模拟计算中对模型施加位移约束条件，其中模型的底面施加全位移约束条件，模型的两侧施加竖向位移约束，模型的顶部为自由边界条件。

表1 计算材料的物理力学参数

2.3 计算方案

根据相关研究成果，在大坝建成蓄水之后，沥青混凝土心墙的坝肩部位会出现比较明显的拉应力，也就是在上游水压力荷载的作用下，坝轴线会产生不同程度的拉伸和变形。为了检验心墙曲率对大坝受力特征的具体影响，研究中根据不同的心墙曲率，设置了两种计算方案：方案1，心墙曲率为9.6×10-5/m；方案2，心墙曲率为1.1×10-5/m。构建不同计算方案下的大坝有限元计算模型，分析不同心墙曲率下的静力特征。

3 计算结果与分析

3.1 应力

研究中利用已构建的计算模型，对两种不同心墙曲率计算方案下蓄水期大坝大、小主应力进行计算分析，根据计算结果，绘制出如图1所示的坝体最大截面应力等值线图。由图1可知，在不同的心墙曲率条件下，大坝截面的大（小）主应力等值线分布规律基本相似，呈现出自上而下逐步增大的特征。其中，大、小主应力的最大值出现在大坝底部的中间部位，而最小值则出现在大坝顶部。从具体的数值来看，在方案1的条件下，心墙承受的最大大、小主压应力值分别为2.38，1.39MPa；在方案2的条件下，心墙承受的最大、最小主压应力值为2.44，1.41MPa。由此可见，随着心墙曲率的增大，心墙承受的最大压应力没有明显变化，拉应力得到消除，几乎减小为0。

图1 坝体最大截面应力等值线图

总之，随着心墙曲率的增大，大坝各个部位的压应力值有所增大，但变化并不明显；坝肩部位的拉应力值则明显减小或消失。由此可见，采用曲心墙可以明显改变大坝的应力分布特征，可以起到比较显著的消除坝肩拉应力的作用。

3.2 位移

研究中利用已构建的计算模型，对两种不同心墙曲率计算方案下蓄水期大坝坝轴向、顺河向、竖向进行计算分析，根据计算结果，绘制出如图2—4所示的位移等值线图。由图2—4可知，两种不同计算方案下的坝轴向、顺河向、竖向等值线分布规律基本相似；在不同的心墙曲率条件下，坝轴向位移的数值较小，且没有发生明显的变化，分别为4cm和5cm，说明沥青混凝土心墙的曲率对大坝坝轴向位移的影响极为有限；大坝顺河向最大位移值仅增加了1cm，说明心墙的曲率变化对大坝顺河向位移基本没有影响；随着心墙曲率的增大，大坝竖向最大位移值仅增加了2cm，说明心墙的曲率变化对大坝竖向位移的影响不大。

图2 坝轴向位移等值线图

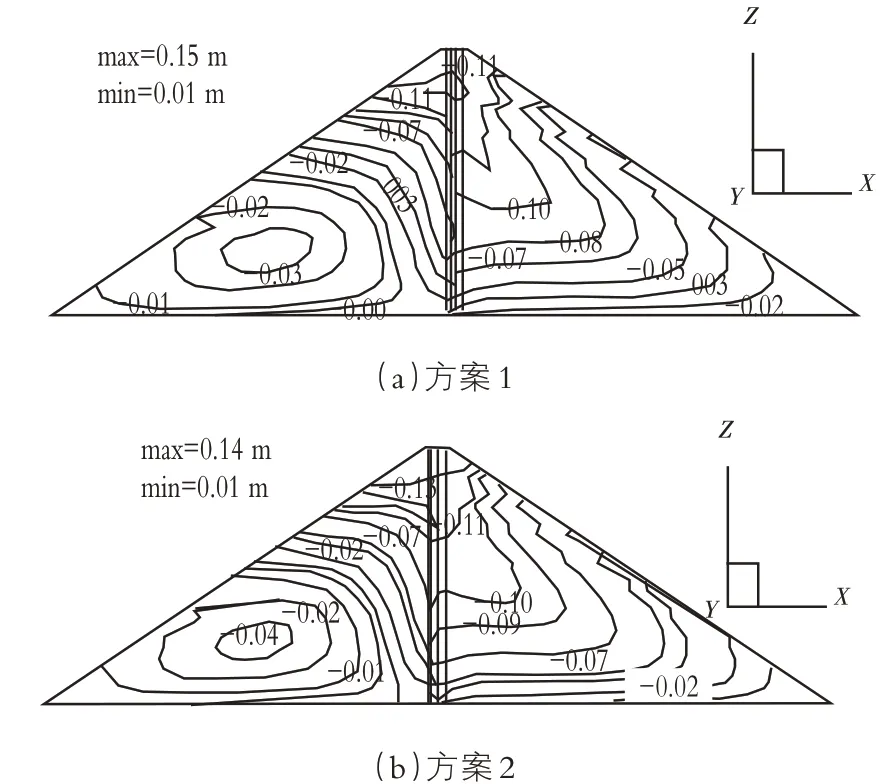
图3 顺河向位移等值线图

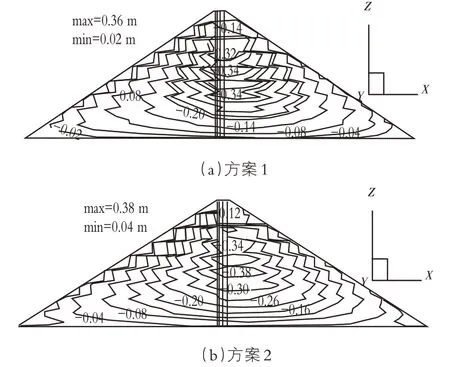
图4 竖向位移等值线图

总之，大坝的位移是自重荷载和上游的库水压力共同作用的效果，在其他条件不变的情况下，坝体的受力及分布基本保持不变，因此心墙曲率的变化不会对大坝位移产生比较明显的影响。

4 结语

综上，利用数值模拟方法，研究心墙曲率变化对大坝应力位移特征的影响，得出：采用曲心墙可以明显改变大坝的应力分布特征，可以起到减小或消除坝肩拉应力的作用，且心墙曲率越大，上述作用越明显；心墙曲率的变化不会对大坝位移产生比较明显的影响。因此，在沥青混凝土心墙大坝设计过程中，可以结合实际情况选择曲心墙直坝坝型结构。