基于椭球体放矿理论的后和睦山采场结构参数优化

2021-10-22李国平董亚宁

现代矿业 2021年9期

李国平董亚宁

（1.姑山矿业有限责任公司；2.安徽马钢罗河矿业有限公司）

无底柱分段崩落法是和睦山铁矿-200 m中段后和睦山矿段主体的采矿方法，也是未来深部（-200~-300 m）推荐的采矿方案［1-3］。在目前的回采过程中，由于无底柱分段崩落法采场结构参数布置不合理，导致2条进路之间的脊部部分矿石在下一分段难以放出。为尽可能回收脊部残留矿石，矿山在-162.5 m水平原有2条进路之间增加1条进路。由于增加进路后，进路之间的间距缩小，矿柱所受压力增大，为防止进路变形影响设备通行，新增进路规格加大至3.4 m×2.8 m。增加进路后，进路之间的间距由原来的12 m变为6 m，相邻2条进路之间脊部矿柱宽度仅为2.7 m。由于进路间距过小，进路间脊部矿柱变薄，进路所受地压增大，安全性变差。因此，必须在总结当前进路间距使用效果的基础上，通过理论分析，优化无底柱分段崩落法进路间距，为-200 m中段其他分段和深部-200~-300 m各分段采场布置提供科学依据，从根本上解决困扰矿山的采场结构参数难题。

本研究以优化后的采场结构参数［4-5］可以获得良好的矿石回收效果为目标，基于崩落矿石的流动规律，分析多漏斗放矿［6-7］时的松动椭球体形态，找到导致问题出现的根本原因。在分析后和睦山矿段无底柱分段崩落法开采现场数据基础上，通过理论计算，确定最佳采场结构参数。

1 椭球体放矿理论［8-10］

崩落矿岩散体放出过程中的整体流动研究，主要是放出椭球体理论的研究。根据现场实际放矿经验及室内石子放出试验，该部分矿石在原有空间中的形状为椭球体，随着矿石从底部的放出，不同放矿水平会形成放矿漏斗，如图1所示。

1.1 崩落矿岩散体整体流动特性［11-12］

1.1.1 放出体

通过底部放矿结构放出的松散矿石体积量为Q，该部分矿石称为放出体，放出体在原采场中为椭球体形状，如图2所示，且其体积为

式中，Q为放出体体积，m3；a为椭球体长半轴，m；b为椭球体短半轴，m；ε为椭球体偏心率。

为了应用方便，用被截椭球体高度h和放矿漏斗半径r来表示a和b，则

1.1.2 松动体

由图3可知，当采场放出矿石量Qf后，上部松散的矿石松动并填补放出空间，矿石的松散系数取Ke，第n次矿石放出后剩余空间即

由此得出

式中，nQf为放出散体Qf后的剩余空间。

松动椭球体与放出椭球体之间的数学表达式为

由式（8）可得二次松散系数

1.2 多漏斗放矿时相邻漏斗的相互关系研究

后和睦山矿段属于多个放矿出口同时放矿，研究在这种条件下进行放矿时崩落矿岩的运动规律，可以有效地解决采场结构参数优化问题。实践证明，多漏斗进行放矿时，相邻漏斗的松动椭球体有不相互影响、相切和相交3种情形。

相邻松动椭球体相交漏斗脊部残留的矿石量最小，其中多漏斗放矿与崩落矿石层高度h、漏斗轴线间距ld和漏斗口直径d有关。增大h和d，减少ld，能够提高矿石回收率。

1.2.1 相邻松动椭球体不相互影响

如图4所示，在相邻松动椭球体相互不影响的情况下，可得

式中，ld为放矿漏斗轴线间距，m；Bs为松动椭球体短半轴，m；B为放出椭球体短半轴，m；R为放出漏斗最大半径，m。

1.2.2 相邻松动椭球体相切

如图5所示，在相邻松动椭球体相切情况下，可得

1.2.3 相邻松动椭球体相交

如图6所示，在相邻松动椭球体相交情况下，可得

2 后和睦山矿段脊部残留的原因分析

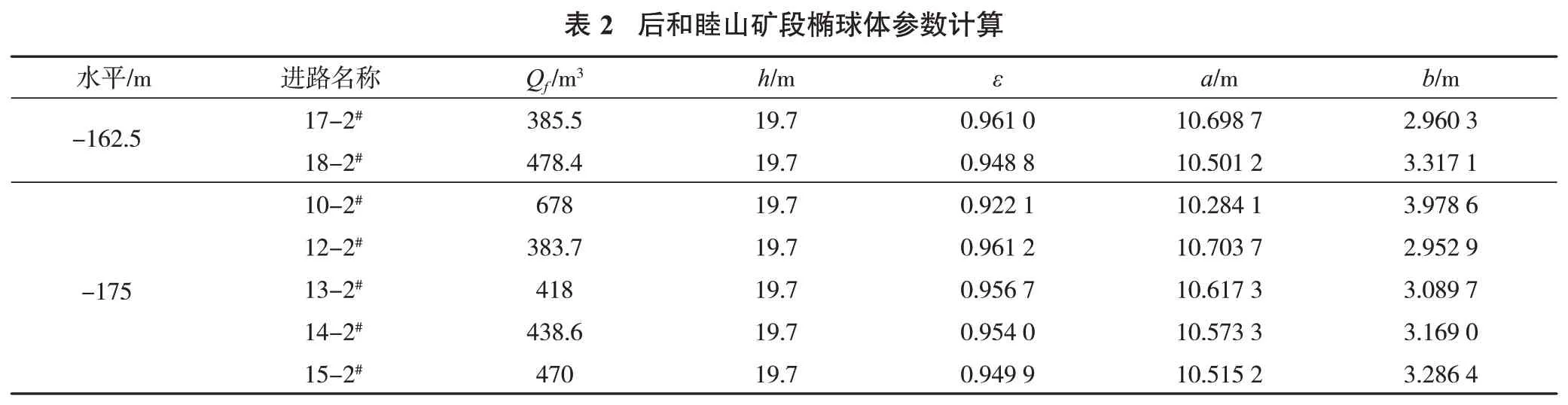
由表2可得，放出椭球体短半轴b的取值范围是2.95~3.98 m。由于放出体短半轴与松动椭球体短半轴bs的关系为bs=2b，则bs的范围是5.90~7.96 m。后和睦山矿段目前使用的进路间距ld为12 m，计算出的松动椭球体短半轴bs主要满足式（10）、（11），即相邻松动椭球体为1.2.1节和1.2.2节2种状态，只有10-2#进路的椭球体形态满足式（12）。由此可知，调整进路间距使放矿体相交才能提高后和睦山矿石回收量。