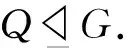同阶交换子群个数之集为{1,3}的有限群
2021-10-21陈贵云
钱 焱,陈贵云
西南大学 数学与统计学院,重庆 400715
有限群的结构一直是群论研究中一个最基本的课题,而群的性质与结构都能从它的固有数量反映出来,例如:奇数阶群可解; 若G的Sylow子群的个数之集为{1},则G为幂零群.
因此,通过子群的数量特征来研究群G的结构是极其有意义的.比如,许多群论学者研究了子群共轭类的类数、 非正规子群的个数及阶、 极大交换子群的阶之集,以及当同阶子群个数之集为简单集合时对群结构的影响,有关这方面的成果可参见文献[1-12].
本文关注同阶交换子群个数与群结构的关系,并讨论了当群G的同阶交换子群个数之集为{1,3}时群G的结构.当然这类群是存在的,如S3就满足此条件.另外,本文也证明了同阶交换子群个数之集为{1,2}的有限群是不存在的.因此,研究满足同阶交换子群个数之集为{1,3}的群G的结构是有意义的.
本文将证明如下定理:
定理1设G是有限群,则下列结论成立:
(a) 不存在有限群G,使得其同阶交换子群个数之集为{1,2}.
(b)G的同阶交换子群个数之集为{1,3}的充要条件是G同构于下列群之一:
(b1)G=〈u〉×(〈b〉×|〈a〉),其中uk=1,a2m=1,b3=1,a-1ba=b-1,2⫮k,3⫮k;
(b2)G=〈v〉×Q8,其中2⫮o(v),Q8为四元数群;
(b3)G=〈w〉×G2,其中2⫮o(w),G2为(2n-1,2)-型交换群;
(b4)G=〈d〉×G2,其中2⫮o(d),G2为半广义四元数群,且G2=〈e,f〉,e2n-1=1,f2=1,f-1ef=e1+2n-2,n≥4.
由文献[11]的定理4.3得:若G的同阶子群个数之集为{1,3},则G只可能同构于以上(b1)-(b4)群之一.因此得到下面的推论:
推论1设G为有限群,则下列结论等价:

为了证明定理1,先引入以下引理:
引理1[12]设P是一个包含唯一p阶子群的p-群,那么或者P是循环群,或者p=2且P是广义四元数群.
引理2[13]设|P|=pn,1 引理3设p∈(G),P∈Sylp(G),且G的同阶交换子群个数之集为{1,3},则 证若P有唯一p阶子群,则由引理1即可得到成立. 引理5[14]二面体群D8有5个2阶子群,3个4阶子群. 引理6[11]设G为广义四元数群,sk(G)表示G的2k阶子群的个数,则 引理7若|G|=8,且G的同阶交换子群个数之集为{1,3},则G只可能是(4,2)-型交换群或四元数群Q8. 证由文献[15]的3.4.3知,8阶群在同构意义下共有5类,分别是C8,C2×C2×C2,C4×C2,Q8,D8.下面将分别计算每个类的同阶交换子群个数之集. 因为C8为循环群,所以它的各阶子群个数都为1,且均为交换群,从而C8的同阶交换子群个数之集为{1}. 因为C2×C2×C2的各阶子群均为交换群,且其2阶子群的个数为(23-1)/(2-1)=7,4阶子群的个数为[(23-1)(22-1)]/[(22-1)(2-1)]=7,所以C2×C2×C2的同阶交换子群个数之集为{1,7}. 不妨设 C4×C2=〈a,b:a4=1,b2=1,[a,b]=1〉 易知C4×C2的各阶子群都为交换群,且2阶子群有3个,分别为〈a2〉,〈b〉,〈a2b〉; 4阶子群也有3个,分别为〈a2〉×〈b〉,〈a〉,〈ab〉.所以C4×C2的同阶交换子群个数之集为{1,3}. 因为Q8=〈a,b:a4=1,a2=b2,b-1ab=a-1〉,且其真子群均为交换群.由引理6可计算得:其2阶子群有1个,即〈a2〉; 4阶子群有3个,分别为〈a〉,〈b〉,〈ab〉.因此,Q8的同阶交换子群个数之集为{1,3}. 由引理5知8阶二面体群D8的同阶交换子群个数之集为{1,3,5}. 引理8[16]设P为16阶非交换2-群,且P的同阶交换子群个数之集为{1,3},则P只能为半广义四元数群,定义关系为P=〈a,b:a8=b2=1,b-1ab=a5〉. 引理9[13]设P为一个具有循环极大子群的2-群,则P只有以下6种互不同构类型的群: 引理10[15]设G为非交换群,且它的所有Sylow子群循环,则G为亚循环群,G=〈a,b〉,am=bn=1,b-1ab=ar,((r-1)n,m)=1,rn≡1(modm),|G|=nm. 引理11[11]设G是(pn,pm)-型交换p-群,其中m≤n.则群G的pk阶子群的个数为 定理1的证明 证(a) 设p∈π(G),P∈Sylp(G). 若P有唯一p阶子群,则或者P为循环群,或者p=2且P为广义四元数群.当P为广义四元数群时,由引理6计算得其4阶子群个数至少为3,矛盾.当P为循环群时,因为G的Sylowp-子群个数为n=1+kp,所以n=1,或者n≥3.又因为G的同阶交换子群个数之集为{1,2},所以n=1.进而得到G的所有Sylow子群正规且循环,故G为循环群,从而G的各阶子群个数都为1,不满足题设条件.若P有两个及以上的p阶子群,则同引理3所证可得p+1=2,这与p≥2矛盾.综上所述,结论(a)得证. (b) 由引理3和引理4知G=H×|G2,其中H循环且2⫮|H|.下面分两种情况进行讨论: 情形1 若G2有唯一2阶子群,则G2或为循环群或为广义四元数群. 先证n=1.因为|Syl2(G)|=3,所以|G3∶NG3(G2)|=3,则|NG3(G2)|=3n-1.于是设NG3(G2)=〈b3〉.又因为NG3(G2)=CG3(G2),故[b3,a]=1.因为a-1ba=br,于是b3=a-1b3a=b3r,从而b3(r-1)=1,因此3n-1|(r-1).若n≥2,则有3|(r-1).又因为G3×|G2为亚循环群,所以((r-1)2m,3n)=1,这与3|(r-1)矛盾.因此n=1. 再证r=-1.因为r≢1(mod 3),所以r≡0(mod 3)或r≡-1(mod 3).由假设条件a-1ba=br知(r,3)=1,从而得r≢0(mod 3),于是r≡-1(mod 3).因此r=-1. 可令 T=G3×|G2=〈a,b:a2m=1,b3=1,a-1ba=b-1〉 由定义关系知T的Sylow 2-子群为极大子群且恰有3个,即〈a〉,〈ab〉,〈ab-1〉.对L≤T,若L是2-群,则L含于T的Sylow 2-子群中.因为T的Sylow 2-子群只有3个且循环,因此与L同阶的子群最多有3个.又由Sylow子群共轭及循环知,与L同阶的子群共轭,故与L同阶的子群个数为1或3.如果L不是2-群,则L的阶为2i·3,此时考虑T的阶为2m-1·3的极大子群,可知此极大子群必为〈a2〉〈b〉,〈(ab)2〉〈b〉,〈(ab-1)2〉〈b〉.又由定义关系可知CG2(G3)=〈a2〉,即[a2,b]=1,从而〈b〉×|〈a2〉=〈a2〉×〈b〉为循环群,则 〈a2〉〈b〉=〈(ab)2〉〈b〉=〈(ab-1)2〉〈b〉=〈a2〉×〈b〉 故T的阶为2m-1·3的极大子群只有1个,即为〈a2〉×〈b〉.综上所述,T的极大子群均循环,且同阶极大子群的个数之集为{1,3},进而T的2i·3阶的同阶交换子群个数也为1,符合定理1的条件.综上所述,此时G对应定理1(b)中的(b1)类型群. 情形2 若G2的2阶子群个数为3,对G2是否交换进行讨论. 假设G2为非交换群,则|G2|≥8,故可分为以下几种情形讨论: 证明当n=5时,G2只能是半广义四元数群. 考虑G2的极大子群M.当M交换时,M为循环群或(2r,2s)-型交换群,其中r+s=4.又由引理11知(22,22)-型交换群含有7个4阶子群,这与定理1的条件矛盾,因此M为循环群或(23,2)-型交换群.当M非交换时,若M只有1个2阶元,则M是广义四元数群,然而由引理6知,16阶广义四元数群不满足定理1的条件.若M有3个2阶元,则由上面知M为半广义四元数群.综上所述,M为循环群、 (23,2)-型交换群或16阶半广义四元数群. 当M为循环群时,则G2为引理9中的群,经过计算群的同阶交换子群个数得,G2为半广义四元数群.因为(23,2)-型交换群和16阶半广义四元数群的8阶子群都是交换群且个数为3,又因为G2的同阶交换子群个数之集必为{1,3},则:若M为这两个群之一,则G的8阶子群只能在M的这3个极大子群中,从而G2的每个极大子群的极大子群都含在M内,进而G2中除循环极大子群之外的极大子群都等于M.但G2至少有3个极大子群,因此G2一定至少含有2个循环极大子群,因此G2为引理9中的群,且G2有3个2阶子群,通过计算群的同阶交换子群个数知,G2为32阶半广义四元数群. 假设当n=k-1时,G2是一个半广义四元数群,去证明当n=k时,G2是一个半广义四元数群. 仍然考虑G2的极大子群M.当M为交换群时,M为循环群或(2r,2s)-型交换群,其中r+s=k-1.又由引理9知,当M为非循环交换群时,M只能为(2k-2,2)-型交换群.当M为非交换群时,如果M只有1个2阶元,那么M只能是广义四元数群,但是由引理6计算M的4阶子群个数知,广义四元数群不满足定理1的条件.如果M有3个2阶元,则M的同阶交换子群个数集为{1,3},由归纳假设,M为半广义四元数群.因此,仍然可以得到M为循环群、 (2k-2,2)-型交换群或2k-1阶半广义四元数群.然后同n=5时的证明可得G2为半广义四元数群.综上所述,当和成立时,G都对应定理1(b)的(b4)类型群. 由于定理1中的4种群对应的Sylow 2-子群互不同构,因此定理1(b)的(b1)-(b4)类群互不同构,故定理1结论(b)得证.