基于微电网的DV-hop改进算法

隋 涛， 陈浩然， 刘秀芝， 刘国栋

(山东科技大学电气与自动化工程学院， 青岛 266590)

面对全球常规能源的逐渐枯竭和环境污染，为了响应可持续发展的口号，风能和太阳能等可再生能源已广泛用于微电网[1]。微电网作为智能电网中的一项重要技术，由于各系统分布不规则，没有一种固定的分布模式，传统的电网监测系统不能满足对微电网的监测需求。在微电网监测系统中引入边缘计算技术可以优化数据传输。

无线传感器网络(wireless sensor network，WSN)常用于微电网监测系统中。由于各种不确定性，在WSN中可能产生数据包丢失问题。如果WSN的节点无法正确定位，则网络节点定位误差过大，导致网络无法连接，甚至使网络崩溃，出现丢包问题[2]。常见的WSN定位算法可分为基于测距和非测距的方法，基于测距的定位算法具有定位精度高，成本开销大，对环境要求高的特点，常应用于室内精准定位的场景。而基于非测距定位的算法定位误差高，实现简单成本低，对环境的要求也不高，应用比较广泛且在大多数实际应用中非测距定位算法的粗精度也能满足实际需求。在WSN的定位中，需要考虑网络的定位精密度、节点的通信半径、能量耗损等许多因素。DV-Hop算法是一种非测距定位算法，常被应用于WSN定位中。该算法主要利用节点间相互通信，借助平均每跳跨距与未知节点到锚节点之间跳数的乘积，计算未知节点到锚节点的距离[3]。随后基于经典DV-hop算法，肖美华等[4]提出了一种平均加权(average weighting,AW)方法；程远国等[5]设计了跳数加权(hop weighting,HW)方法；程超等[6]提出了一种误差加权(error weighting,EW)方法；张安安等[7]提出了一种融合无线传感器网络(wireless sensor network, WSN)和射频识别(radio frequency identification, RFID)技术的输电线路杆塔状态监测网络；史进等[8]提出了一种基于病毒体投射机制的移动无线传感网节点定位算法。这些改进在不同水平上增进了DV-hop算法的精度，减小了定位误差。但是若要满足微电网中的信息传输，定位算法不宜过于复杂，否则会影响电网正常运行。

为此，在应用边缘计算技术的基础上改进了微电网监测系统的结构，并在此结构下针对DV-Hop算法[9]进行了一定改进，希望能进一步减小DV-Hop算法的定位误差。

1 微电网监控网络

1.1 传统微电网分布式电源模块监控系统

微电网作为智能电网领域的重要一环，部署了各种分布式电源，其结构复杂。例如珠海某海岛微电网就包含光伏发电设备、光伏并网柜、风电并网柜、柴油发电机、多项变流控制器、风力发电设备等设备，需要在使用大量的监测设备对微电网各部分运转状态进行监测。

传统的微电网分布式电源模块监控系统如图1所示。微网设备信号由无线传感器采集并传递给网关，随后控制中心通过处理汇聚节点收到的故障信号，由此可分析该节点发生故障的具体位置和类型[10]。

图1 微电网中某区域分布式电源模块监控系统Fig.1 Monitoring system of distributed generation module in microgrid

1.1 基于边缘计算的分布式电源模块监控系统

在微电网监控系统中，将全部监测的节点构成一个无线传感器网络，会给汇聚节点带来巨大的压力。若其中部分节点发生故障，不能被正确定位，可能会危及整个网络，从而影响整个微电网监控系统。在微电网中运用边缘计算技术可以缓解微电网运行时信息拥堵的问题。边缘计算作为在网络边缘执行计算的一种模式，用于应对大量物联网终端设备的使用所带来的对带宽负载、网络稳定性的挑战[11]。

将微电网的监测区域按照地理位置或运行结构分割成多个监测区域，每个监测区域的无线传感器节点将采集到的信号上传至边缘服务器，再由边缘服务器进行初步信号处理后传输至云端服务器。基于边缘计算的分布式电源模块监控系统如图2所示。

面对监测数据过多，云计算中央服务器处理性能有限等，通过对采集信号进行基于边缘计算的预处理，芟除采集信号的冗余信息或错误信息，将一些采集信号分析技术下沉到边缘处，以此减少对云中心的计算、存储和网络带宽需求，提高数据分析的效率。

通过对监控区域分割，各个区域相对独立，减小了汇聚节点的工作量，降低了数据传输时网络堵塞的可能性。在图2的监测区域中，一些传感器设备上加装了GPS定位系统，可以将这些设备看做无线传感器网络中的锚节点。因此，图2中的监测区域可以抽象为图3的仿真场景[10]。

图2 基于边缘计算的分布式电源模块监控系统Fig.2 Distributed power module monitoring system based on edge computing

图3 监测区域网络仿真场景Fig.3 Simulation scenario of monitoring area network

由于加装全球定位系统(global positioning system, GPS)后会使传感器节点能耗增加从而缩短节点寿命，同时为了节省成本，在分布式发电过程中，只有少数设备配备了GPS传感器节点，而大量设备的位置未知。锚节点的位置已知，所提出的定位算法是一种以少量已知位置的设备来定位位置不确定的设备的算法。在监控过程中，每个设备的节点都通过无线链路向监控中心传输诸如电压、电流等数据。当监控中心发现某设备损坏，需要及时获知损坏设备位置，否则会引发严重后果。

2 DV-Hop定位算法

2.1 经典DV-Hop算法

DV-Hop算法靠锚节点(anchor node，AN)和未知节点(unknown node，UN)的平均跳距和跳数之积得到UN到AN的距离。

算法流程如图4所示。锚节点标识设为i，锚节点位置坐标记为ANi。ANi的平均每跳距离(average hop distance, AHD)记为AHDi，其计算公式为

图4 DV-Hop算法流程图Fig.4 DV hop algorithm flow chart

(1)

式(1)中：N为AN的总数；(xi,yi)、(xj,yj)分别为ANi和ANj的坐标；hij为从ANi到ANj的最小跳数。

设di为UN到ANi的估计距离，其计算公式为

di=AHDhopi

(2)

式(2)中：hopi为从UN到ANi的最小跳数；AHD为UN保存的平均每跳距离。

2.2 DV-Hop算法误差分析

从定位过程来看，影响DV-Hop算法精度的主要因素有：计算节点位置的方法、节点间的预计距离、最低跳数以及平均每跳距离[12]。

DV-Hop算法中，当传感器节点记录到相同的最小跳数，但间距不同或是跳数不相等，间距相同时会产生最小跳数误差。如图5(a)所示，节点C的最大通信半径记为R，节点A至节点C的距离与节点G至节点C的距离相似，但节点C至节点A的最小跳数记为2，到节点G的最小跳数为1。节点C到节点B、节点D、节点G的最小跳数均为1，而节点C到节点B、D、G的距离不相等。

同理，如图5(b)所示，节点A到节点J的实际间距为R，节点A到节点D的实际间距为R，但是这两者的跳数却并不相同。图5(c)中，节点A到节点B跳数为1跳，节点A到节点F跳数也为1跳，但是其距离并不相同。所以此种最小跳数的计数方法会带来较大的误差。

平均每跳距离AHD的误差受WSN中节点分布不均匀的影响，如图5(a)所示，假设节点A、节点C、节点G为3个锚节点。由图5可知，锚节点C和锚节点G的AHDCG计算公式为

图5 传感器节点分布示意图Fig.5 Sensor node distribution diagram

AHDCG=(R-ε)/1

(3)

式(3)中：ε为距离测量误差。

锚节点C和锚节点A之间的AHDCA计算公式为

AHDCA=(R+ε)/2

(4)

计算UN和AN的间距将参考附近的锚节点AHD，但AN间的平均跳距也会有较大的误差。最近锚节点的单个AHD几乎不能反映UN周围的网络特性，这可能会导致较大定位误差[13-14]。

2.3 DV-Hop改进算法

DV-Hop算法的长处是简单易实现，缺点是较低的定位精度。为了减小锚节点间平均跳距引起的误差，锚节点提供的信息被大量使用可以提升估计的UN的AHD的精度[13]。文献[4]提出了AW方法，利用多个锚节点的AHD，取平均值来代替传统算法中未知节点的AHD，可表示为

(5)

式(5)中：AHDu为n个锚节点AHD的平均值；n为UN从中获取信息的锚节点的数目，n≤N。每个AN具有相同的权重值。

锚节点距离未知节点越近，其网络位置信息与未知节点越相近。基于上述假设，文献[5]设计了HW方法。

(6)

(7)

式中：ωi为跳数权重值；hui为UNu到ANi的最小跳数。

令锚节点的AHD准确度提高的一种方法是减小锚节点的距离误差。文献[6]提出了EW方法，权重值ω计算公式为

(8)

(9)

式(9)中：εi为ANi的平均每跳距离误差；εj为ANj的平均每跳距离误差；ω为基于平均每跳距离误差的权重值；hij为从ANi到ANj的最小跳数；dij为从ANi到ANj的估计距离；Dij为实际距离；N为WSN中所有锚节点的数量。

2.4 基于AW与HW的DV-Hop改进算法

当锚节点部署在网络边沿时，大多数未知节点可被定位。当锚节点分布在网络中心时，远离中心的节点累积定位误差较大，导致总体定位精密度减小[4]。对文献[4]实验结果分析可知：当锚节点在网络边缘布置时，定位精度最好。当锚节点分布在监测区域边沿时，平均加权方法效果最优秀。文献[5]用网络的拓扑关系估计出的空间直线距离替代节点间的跳距关系进行运算，在锚节点所占比例较低时，网络能够确定连通的区域内的所有未知节点位置[5]。

应用了跳数加权的DV-hop算法在一般情况下可以取得较好效果。由于在应用了边缘计算技术的微电网监测区域中，每一个区域面积较小，因此锚节点更容易部署在区域边缘。因此将适用于锚节点分布于监测区域边缘的平均加权方法应用到跳数加权方法上可以取得更好的效果。在AW方法与HW基础上进行适当的改进，可表示为

(10)

(11)

AHD=AHDu+|ω1-ω2|

(12)

式中：ω1为基于平均加权方法的改进权重值；ω2为基于跳数加权方法的改进权重值。

3 仿真实验与分析

3.1 实验环境及参数设置

基于MATLAB2016a软件，在内存为8 G，CPU为Intel Core i7处理器，操作系统为Windows 10的计算机上进行。针对图2各个小范围监测区域，模拟了一个200 m×200 m的正方形监测区域。设备总数设为200，即有200个无线传感器节点。参考实际户外微电网运行状况，GPS定位误差设置为 5 m。从经济方面以及网络正常运行方面考虑，锚节点覆盖率取20%，通信半径为30 m。由于微电网架构灵活多变，因此对各传感器位置进行随机设置，仿真多次，取平均值。每次实验的相对定位误差计算公式为

(13)

式(13)中：未知节点的估计坐标由(xest,yest)表示;未知节点实际坐标由(xtrue,ytrue)表示；传感器节点的最大通信半径为R；Nnum为未知节点数目。

平均定位误差的计算公式为

(14)

式(14)中：ξi为每次实验的相对定位误差；Ttime为实验次数。

3.2 仿真实验结果分析

本次实验分为两组对照实验，一组为普通DV-hop算法、应用了平均加权方法的DV-hop算法、应用了平均加权与跳数加权的DV-hop算法(本文方法)这3种DV-hop算法进行对比，按照多个算法步骤分别进行，选出性能较优的算法；二组为接收信号的强度指示(received signal strength indication，RSSI)方法(未知节点利用邻居锚节点进行定位，没有邻居锚节点的未知节点无法定位)、RSSI改进方法(有邻居锚节点的未知节点只利用邻居锚节点进行定位，没有邻居锚节点的未知节点才利用已经定位了的邻居未知节点进行定位)、Centroid方法与一组选出的较优DV-hop算法进行对照实验，同样按照多个算法步骤分别进行100～500次，间隔次数为100的实验。一组对照实验结果如图6所示，一组对照实验平均误差如表1所示，二组对照实验结果如图7所示，二组对照实验平均误差如表2所示。各算法优缺点如表3所示，各算法不能被定位的节点数如表4所示。

表2 应用了平均加权与跳数加权的DV-hop、RSSI、 改进的RSSI、Centroid算法平均误差

表3 各算法优缺点比较

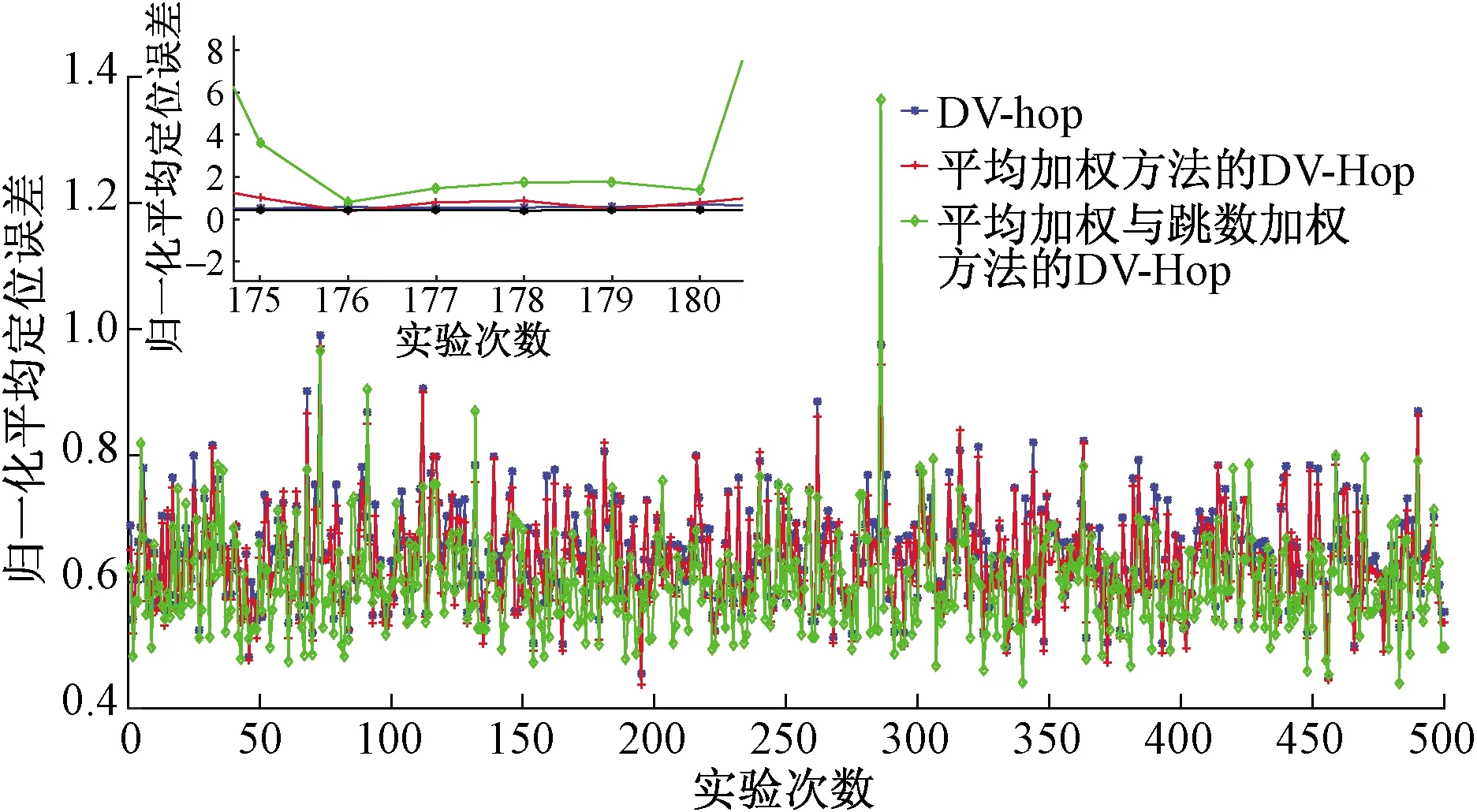
图7 应用了平均加权与跳数加权的DV-hop、RSSI、 改进的RSSI、Centroid算法仿真结果图Fig.7 Simulation results of average weighted and hop weighted DV-hop, RSSI, improved RSSI and Centroid algorithms

表1 DV-hop、应用了平均加权的DV-hop、应用了 平均加权与跳数加权的DV-hop算法平均误差

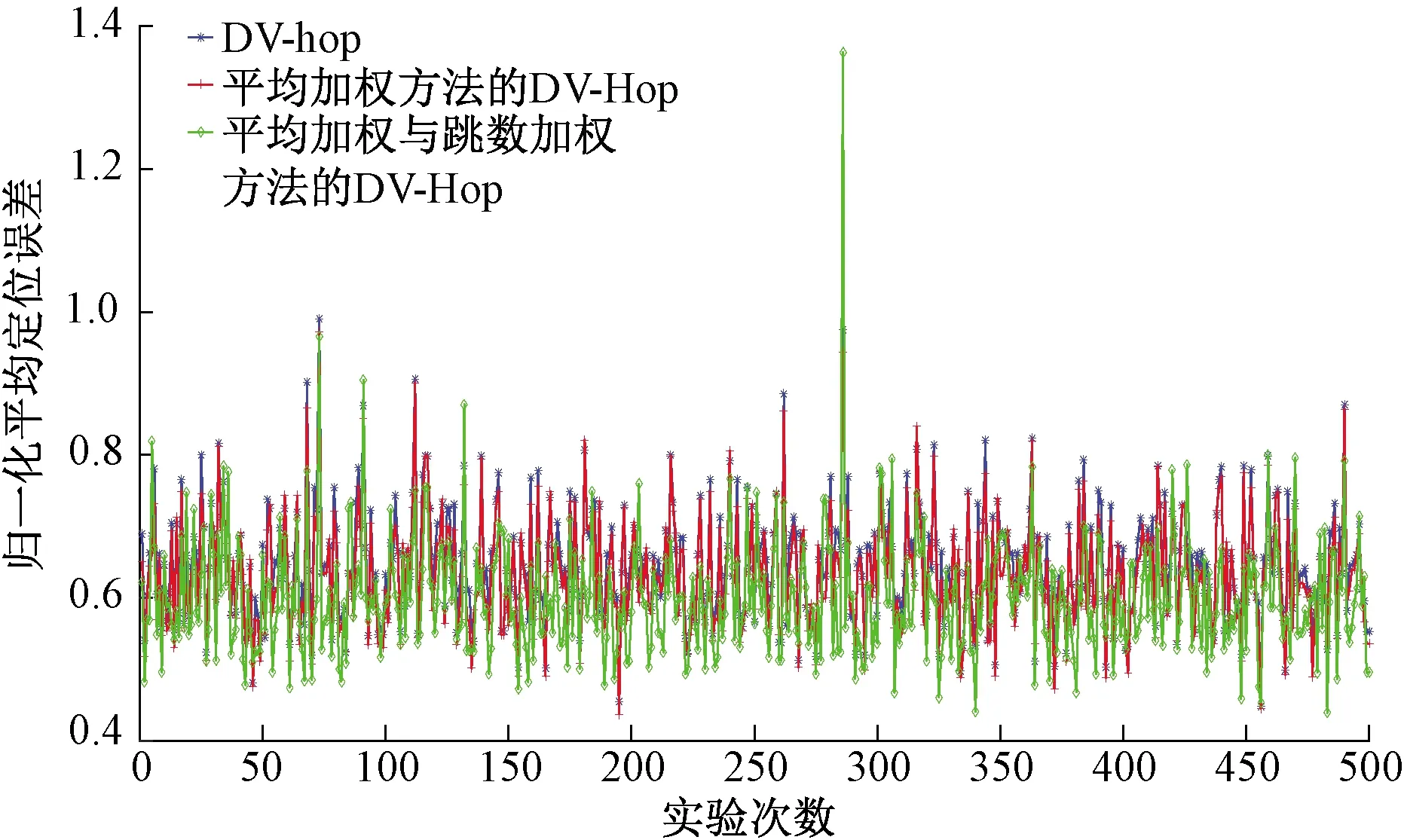
图6 DV-hop、应用了平均加权的DV-hop、应用了 平均加权与跳数加权的DV-hop算法仿真结果Fig.6 Simulation results of DV-hop, DV hop with average weighting and DV hop with average weighting and hop number weighting

在本次实验设定的微电网场景中，由于每个监测区域较小且节点较多，运用DV-hop算法与Centroid算法可以得到较小的平均误差，而RSSI算法则会产生较大定位误差，不适用于此场景。DV-hop与Centroid算法对比，虽然Centroid算法的平均误差较小，但是其运行时间比起DV-hop算法来说特别长，不能满足微电网实际运行时的需要，而且运用该算法会有不能被定位的未知节点，可靠性会下降。因此DV-hop算法从定位精度，定位可靠性与实时性上来说优于其他两种算法。本次实验的3种DV-hop算法，所提出的平均加权与跳数加权的DV-hop对比普通DV-hop算法精度提高了6.88%，对比平均加权方法的DV-hop算法精度提高了5.12%，通过运用本文方法可以取得较小的平均误差。

4 结论

针对每个监测区域较小且节点较多的特点，在引入平均加权方法的改进DV-Hop算法基础上，提出了基于平均与跳数加权的DV-hop算法。该改进算法对比已有算法减小了定位误差，且不会增加运算时间，可以适应基于边缘计算的微电网无线传感器网络定位场景。边缘计算技术引入微电网监测系统，提高了信息传递效率，改进了微电网监测系统结构。改进的无线传感器定位算法可以提高定位精度，在微电网监测中具有广阔的应用前景。