纳米流体在热虹吸管中换热性能数值研究
2021-10-21袁明森贺铸谭方关
袁明森,贺铸,谭方关
(武汉科技大学 省部共建耐火材料与冶金国家重点实验室,湖北 武汉 430081;武汉科技大学 钢铁冶金及资源利用省部共建教育部重点实验室,湖北 武汉 430081)
热虹吸管(重力热管)是一种在两相传热机制下工作的冷却装置,不仅可以在有限空间内传递大量的热量,而且同时具备无需外部能量消耗、无噪音、节能、体积小、结构简单和工作可靠等优点[1],所以被广泛应用于石油化工节能[2-4]、余热回收[5-6]和相变储热技术[7]等领域.随着碳中和理念的提出,节能环保要求愈加严格,工业炉余热利用率要求不断提高,而优化重力热管的换热性能是解决该问题的有效途径.
为了寻求重力热管的最佳换热性能,研究人员发现重力热管在达到最优运行状况时会受限于重力热管的工作功率、倾斜角度、填充率与工作介质的影响.Zhao等[8]通过数值模拟的方法探究不同加热功率对热管性能的影响,结果表明热管热阻随着加热功率增加不断减小.倾斜角度越大,热管的换热性能表现更优[9-10].刘玉清等[11]通过水工质重力型分离式热管换热性能试验发现,热管在实际安装时应处于竖直状态以获取最大的换热性能.李本文等[12]、卿倩等[13]采用数值模拟研究了不同填充率对重力热管性能的影响,发现随着填充率的增加,热管热阻减小.但是禹法文等[14]、Alizadehdakhel等[15]发现当加热功率超过一定值后,填充率增加,热阻反而增大,热管性能恶化.由上可知,不仅不同因素对热管换热性能的影响程度有所差异,而且热管内部工质种类与热管换热表现也有直接关系.近年来,纳米流体作为具有良好的换热性能新工质,在热管换热领域饱受关注.
与传统工质类似,通过调整纳米流体工质中纳米颗粒的粒径、基质和基液种类以及两者所占体积分数都能实现对其热阻等换热性能的优化[16].胡浩等[17]通过数值模拟探究水基氧化铝纳米流体体积分数变化对重力热管的换热性能的影响,结果发现纳米流体体积分数为6%时热管的热阻最小,相比于纯水热阻减小9.8%.然而,实际过程中纳米颗粒会析出并附着在壁面上,从而影响换热性能,但是这部分附着的含量较少.在忽略上述问题的基础上,张燕辉等[18]、Gupta等[19]采用单相参数模型计算的结果与实验结果吻合较好,这说明如果将纳米流体视为单相物性参数进行分析,其计算结果也具有良好的可靠性.
因此,本文基于 ANSYS Fluent软件建立等效单相纳米流体重力热管数值模型,使用正交实验方法分析不同操作因素下水基氧化铝纳米流体热管内部的蒸发冷凝相变和传热过程,得出各操作因素对热管各段的温度平均值、热阻、等效对流换热系数的影响程度,并基于管内气液两相流变化形态的分析探究操作因素对换热性能影响的机理.
1 计算理论
1.1 VOF模型(Volume of Fluid Model)及控制方程
热管工作过程中会产生相变,气液相界面运动较为剧烈,所以模拟计算采用VOF模型建立基础流动模型.VOF模型是欧拉-欧拉法的一种,其特有的相体积率α几何重构算法能够精确追踪2种或多种不相溶液体的界面位置,能够很好地捕捉气液两相分离,实现相变过程热质传递现象的模拟.在每个计算单元中,所有组分的体积分数之和为1,即如果αl为液相的体积分数,αv为气相的体积分数,则在每个计算单元中存在3种情况:(1)αl=1表示单元全部为液相;(2)αl=0表示单元全部为气相;(3)0<αl<1表示单元处于气液共存状态.
热管内部工作流体的运动状态由连续性方程、动量方程和能量方程这3个方程来描述.
连续性方程:
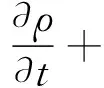
(1)
式中:ρ为密度,kg/m3;u为速度矢量,m/s;t为时间,s.
其中密度ρ的计算式为
ρ=αlρl+αvρv.
(2)
式中:ρl,ρv分别为液相、气相的密度,kg/m3.
动量方程:
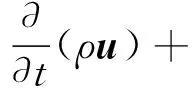
(3)
式中:p为压力,Pa;μ为动力黏度,Pa·s;I为单位张量;g为重力加速度,m/s2;FCSF为表面张力[20],N/m.其中,
μ=αlμl+αvμv;
(4)
(5)
σlv=0.098 058 56-1.845×10-5T-2.3×10-7T2.
(6)
式中:μl,μv分别为液相、气相的动力黏度,Pa·s;σlv为气液间表面张力系数,N/m;cl,cv分别为液相、气相的表面曲率;T为温度,K.
能量方程:
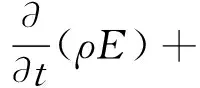
(7)
式中:E为能量,J;k为热导率,W/(m·K);Sq为能量源项,用于计算相变过程中的热量传递,kJ.其中,
(8)
k=αlkl+(1-αl)kv;
(9)
Sq=SamΔH.
(10)
式中:El,Ev分别为液相、气相的能量,J ;kl,kv分别为液相、气相的导热率,W/(m·k);Sam为相变过程中的质量交换量,kg;ΔH为汽化潜热,kJ/kg.
1.2 相变模型
Schepper等[21]提出的稳态相变模型如式(11)~式(16)所示.
蒸发过程(T>Tsat):
(11)
(12)
(13)
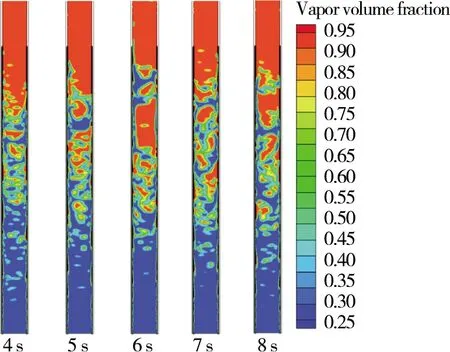
冷凝过程(T (14) (15) (16) 式中:Sm,l和Sm,v分别为相变过程中液相、气相的质量变化量,kg/(m3·s);SE为相变过程中的能量变化量,kJ/(m3·s) ;βe和βc分别为蒸发、冷凝过程的时间松弛因子,s-1;Tsat为饱和温度,K. 当T>Tsat时,计算单元内蒸发过程开始,液相质量减少,气相增加;当T 实验采用水基氧化铝纳米流体作为工质.纳米流体的有效密度计算关系式[22]为 ρnf=(1-φ)ρf+φρnp. (17) 式中:ρnf,ρf,ρnp分别为纳米流体、基液、纳米颗粒的密度,kg/m3;φ为纳米流体的体积分数,%. 采用Drew和 Passman[23]提出的著名的Einstein方程计算纳米流体的黏度: μnf=(1+2.5φ)μf. (18) 式中:μnf,μf分别为纳米流体、基液的黏度,Pa·s. 纳米流体的比热容[24]的计算式为 (Cp)nf=(1-φ)(Cp)f+φ(Cp)np. (19) 式中:(Cp)nf,(Cp)f,(Cp)np分别为纳米流体、基液、纳米颗粒的比热容,J/(kg·K). 纳米流体的导热系数,可采用Yu[25]提出的修正模型进行计算: (20) 式中:knf,knp,kf分别为纳米流体、纳米颗粒、基液的导热系数,W/(m·K);γ为纳米层厚度与纳米颗粒粒径的比值,本文γ取0.2. 热管的传热性能可以用整体热阻[17]来评价,热阻增加,换热性能减弱.热管的热阻计算式为 (21) 式中:R为热管的热阻,K/W;Teav,Tcav分别为蒸发段、冷凝段的平均温度,K;Qin为加热功率,W. 等效对流换热系数[26]是一种综合反映热管内部传热性能的评价指标,是介于蒸发段对流传热系数与冷凝段对流传热系数之间的加权平均值,综合反映热管蒸发段液体沸腾和冷凝段蒸气冷凝2种传热过程,其计算公式为 (22) 式中:heq为等效对流换热系数,W/(m2·K);λ为管壁导热系数,W/(m·K);Le,Lc分别为蒸发段、冷凝段长度,m;di,do分别为热管内径、外径,m; 热管的蒸发段换热性能用蒸发段对流换热系数[25]评价,其计算公式为 (23) 式中:he为蒸发段对流换热系数,W/(m2·K). 热管的冷凝段换热性能用冷凝段对流换热系数[27]评价,其计算公式为 (24) 式中:hc为冷凝段对流换热系数,W/(m2·K);Qc为输出热功率,W. 计算模型的参数参考文献[28]的实验模型参数,几何参数为外径9.52 mm,内径8.32 mm,全长250 mm,冷凝段与蒸发段各为100 mm,绝热段为50 mm.热管结构及网格划分如图1所示.对网格数分别为12 688,24 754,68 520进行计算,结果显示当网格数高于24 754时,网格数对热管热阻的影响可以忽略.考虑到精确性与计算时间成本的影响,选择网格数为24 754 的模型进行计算. 图1 热管结构及网格划分 边界条件根据实验测试值[28]设定.蒸发段施加恒热流密度进行加热,计算公式为 (25) 式中:qe为蒸发段热流密度,W/m2. 冷凝段采用水的对流换热,相关计算公式为 Qc=mCp(To-Ti); (26) (27) 式中:m为冷却水流量,kg/s;Cp为水的比热容,J/(kg·K);To,Ti分别为冷却水出、进口温度,K;hc1为冷凝段外壁面对流换热系数,W/(m2·K);T1为冷却水平均温度,K. 绝热段设为绝热壁面.能量方程与动量方程均以二阶迎风格式离散,相体积率和压力的插值分别采用几何重构法和PRESTO法,速度与压力耦合关系由SIMPLE算法处理.计算域初始化温度和压力分别为298 K和7.5 kPa,时间步长为10-4s,计算时长为30 s. 为验证数值计算的准确性和可靠性,将在40 W和60 W加热功率下热管蒸发段、绝热段、冷凝段温度的计算结果与文献[28]的实验结果对比,如图2所示. 图2 不同功率下壁面温度计算值与实验值对比 由图2可知:实验测试的壁面温度与计算的壁面温度在整体上表现出较好的一致性.由于实验过程中用电阻丝缠绕热管外壁面加热导致蒸发段加热不均,加热过程中有一部分热量散失,然而模拟计算中蒸发段边界条件为恒定热流密度加热,蒸发段壁面加热均匀,在热管填充率为60%时,热管75 mm处为蒸汽区,故在加热功率为60 W的工况时,热管75 mm处的壁面温度计算值会高于实验值.尽管如此,图2中模拟计算与实验结果的最大误差为3.10%,还是可以证明计算采用的模型较为可靠和准确. Zhao等[8]的模拟结果表明,当功率从40 W增加至80 W时,热阻下降变化率逐渐减少;李本文等[12]发现在填充率为60%时,热阻下降变化率达到峰值;Sarafraz等[10]发现填充率为60%时,热管当量导热系数最佳;纳米流体体积分数一般在4%左右,过高会使纳米流体稳定性下降[29],换热性能下降;刘玉清等[11]得出倾斜角度为90°时热管换热效果最好.上述文献表明当加热功率为40~80 W,填充率为40%~80%,倾斜角度为30°~90°等单因素条件下热管换热性能表现较佳,基于此,本文采用表1所示工况进行计算. 表1 不同工况下热阻比较 在数理统计中,若某因素下结果极差R值越大,说明该因素对结果影响程度越大,因此通过极差分析可以得出各操作因素对热管换热性能影响程度.分析表1可知:填充率是影响重力热管换热性能最重要的因素,加热功率和倾斜角度次之,纳米流体体积分数的影响程度最小.对比工况3和工况6发现填充率对重力热管换热性能影响最大,此时工况6的加热功率高于工况3,其热阻应小于工况3,而当其填充率低于工况3时,热阻应大于工况3,但最终热阻高于工况3,说明填充率对热管换热性能的影响最大.由此分析得知热管换热性能下降原因有2个:一是当管内填充率过小,蒸发段没有充足的液相来吸收蒸发段壁面上的热量,导致一部分蒸发壁面干烧,这部分壁面温度快速升高,与冷凝段间的温差急剧增加,热管热阻增加,换热性能下降;二是加热功率增加,蒸发段壁面温度继续升高,热管内部换热会进一步恶化. 不同工况下热管等效对流换热系数比较如表2所示.由表2可知:相比于40 W工况下的热管换热性能,当热管在工作功率为80 W、倾斜角度为90°、填充率为80%、氧化铝纳米流体体积分数为4%的工况下运行时,其等效对流换热系数提高了23.30%.热管换热性能提高的原因有3点:一是加热功率增加,蒸发段壁面加热能力增强,气泡产生频率增加,气泡的产生、生长和脱离等过程对蒸发段壁面附近的液相产生微对流,从而强化蒸发段对流换热能力;二是随着氧化铝纳米颗粒体积分数增加,液相区内部的导热能力增强,气泡产生速率增加,气液相界面波动加剧,从而增强蒸发段的换热性能;三是填充率增加,蒸发段区域的湿润面积增大,换热能力增强. 表2 不同工况下等效对流换热系数比较 图3为工况1蒸发段在不同时刻下气相体积分数变化.由图3可知,热管运行4~5 s内, 管内产生气泡量较少,管内相间波动平缓,蒸发段换热能力较弱,蒸发段对流换热系数为1 098 W/(m2·K).这是由于管内加热功率较小,加热管内工质产生气泡的速率较慢.此外,当倾角较小时,重力沿管道轴向上的分力较小,冷凝液回流到蒸发段的回流动力较小.当填充率较小时,蒸发段湿润区域面积较小,干燥表面积较大从而导致换热能力的恶化.因此热管整个蒸发段的传热能力变弱. 图3 工况1蒸发段不同时刻气相体积分数变化 管内流动特性变化与热管换热性能改变关系密切,图4显示了热管在工况4条件下运行时,蒸发段在不同时刻下的流动特性变化.由图4可知,热管在4~5 s内的工作过程中,管内产生气泡较多,随着气泡合并、长大,变成含气率更高、气液混合效果更好的弹状流,此时蒸发段换热能力增强,相比于工况1,蒸发段对流换热系数增加了16.03%.这是由于加热功率增加使得壁面加热能力增强,壁面附近产生更多气泡.同时,当填充率增加,蒸发段内气液两相界面波动增强,蒸发段内湿润面积增加,换热能力也会增强.此外,当氧化铝纳米颗粒体积分数增加后,不仅会减少蒸发段热边界层的厚度,而且也增强了液相区内部的导热能力,使气泡产生速率增加,气液相界面波动加剧从而增强蒸发段的换热性能. 图4 工况4蒸发段不同时刻气相体积分数变化 热管在工况9条件下运行时蒸发段不同时刻气相体积分数变化云图如图5所示.由图5可知,热管在运行4 ~5 s过程中,管内产生大量气泡,管内形成气泡流的流动状态.随着管内气泡数量进一步增加,管内流型在6 s时呈现为弹状流.弹状气泡在蒸汽惯性力的作用下发生破碎,气液两相均匀混合搅拌,在7 s时发展成搅拌流.8 s时大气泡聚合并在管道中心形成柱状流动,而液相则以液膜的方式在壁面上流动,变成环形流,气液两相相对运动剧烈,换热能力较强.相比于工况4,蒸发段对流换热系数增加13.42%.这是由于,随着热量的持续输入,壁面气化核心处产生的气泡数量越来越多,蒸发段液面流动无序性增加,沸腾换热增强.此外,热管倾斜角度增加后,其冷凝段的液相能更快回流到蒸发段,使蒸发段物质传输效率增强. 图5 工况9蒸发段不同时刻气相体积分数变化 热管分别在工况1、工况4和工况9条件下运行时,冷凝段液相体积分数如图6所示,其对应的冷凝段对流换热系数如表3所示.由图6和表3可知,工况9液膜产生量最多,冷凝段对流换热能力最强.这是因为当加热功率增加,蒸发段产生的蒸气流速增大,气液交界面的界面扰动增强,加剧对冷凝段液膜的扰动,使冷凝段换热能力增强.此外,当热管倾斜角度增加,重力分力增大,提供回流的动力较强.但是,当加热功率达到60 W后,继续增大加热功率并不能提高其冷凝段的换热能力. 表3 3种工况冷凝段对流换热系数 热管分别在这3种不同工况下运行时,其冷凝段速度矢量云图如图7所示.工况1和工况4的倾斜角度为30°,工况9的倾斜角度为90°.由图7可知:3种工况下管内蒸气流动与回流液体流动处于分层流动状态,两相相间扰动较强,提高了热管的传热效率.当倾角为30°时,回流动力不足导致工质不能及时回流到蒸发段,从而影响其传热性能;当倾角为90°时,蒸气沿冷凝段中心轴线方向向上运动,此时冷凝液膜受重力作用沿壁面向下流动,两相间速度差增大,相间剪切力增加,使平整液膜表面变成不规则液膜表面,即膜状冷凝在相间作用力的影响下变成珠状冷凝,使冷凝段的内壁面传热热阻下降,冷凝段换热能力提高. 图7 3种工况冷凝段速度矢量 1)填充率是影响重力热管换热性能最重要的因素,加热功率和倾斜角度的影响程度次之,纳米流体体积分数的影响程度最小. 2)蒸发段在换热能力不断增强的情况下,管中流型由气泡流变成含气率更高的弹状流,然后发展成搅拌流,最终变成环形流. 3)气液两相间速度差随着冷凝能力增强而增大,相间剪切力也随之增加,使平整的液膜变成非均匀液膜,热阻减小.1.3 纳米流体的热物性参数
1.4 热管热阻
1.5 等效对流换热系数
1.6 网格划分与边界条件

2 结果与讨论
2.1 模型验证

2.2 热管热阻分析

2.3 等效对流换热系数分析

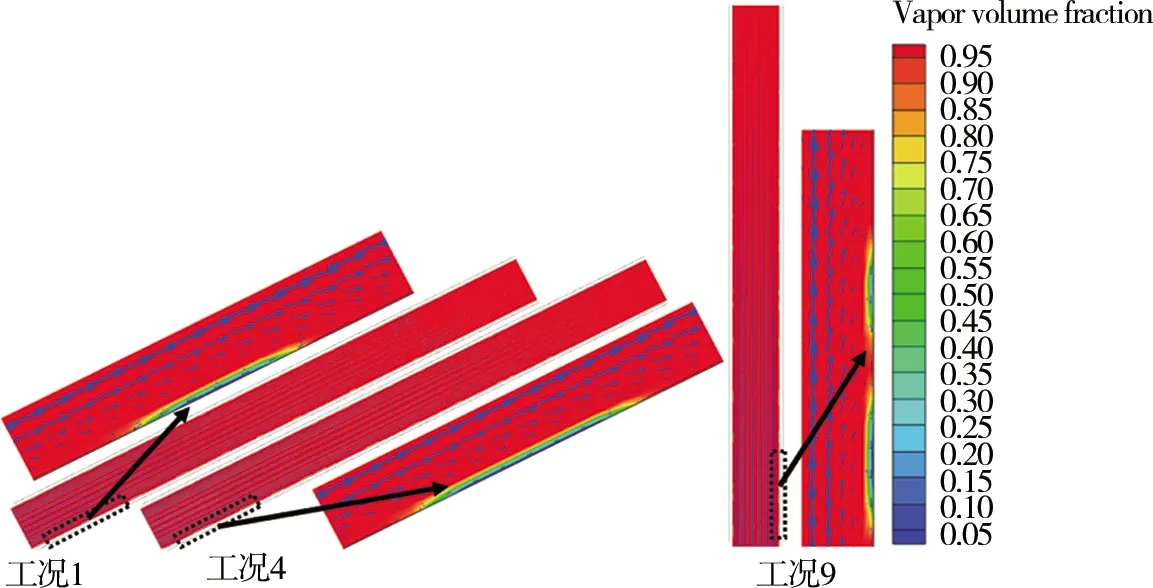
2.4 热管流动特性分析



3 结论
