基于均匀设计的制冷小管径涡流管结构优化

何 鹏，梁裕如，段宏飞，张成斌，刘婷婷

(1.陕西延长石油(集团)有限责任公司 研究院，陕西 西安 710075； 2.陕西延长石油(集团)有限责任公司 管道运输公司，陕西 西安 710075)

引 言

由于涡流管结构简单、不含运动部件，易于加工维修，小幅压降下即能实现大幅降温，可用于深冷前的预冷环节，降低制冷能耗。因此可用于油田井口伴生气的轻烃回收工艺中，对C3、C4进行回收。

涡流管的制冷性能主要取决于操作参数以及结构参数，由于伴生气的压力、温度、流量等操作参数相对固定，因此调整和改进结构参数是实现其制冷性能优化的一种重要手段。计玉帮等[1]研究发现涡流管制冷效应随热端管长增大而减小。Behera U 等[2]对涡流管能量进行了研究，结果表明当涡流管径为 12 mm 时，最优L/D值为25～35，最优的dc/D(冷端管径与涡流管径之比)值为 0.58。何丽娟等[3]对涡流管结构参数进行数值研究，在冷孔板直径为 2.62 mm时，涡流管获得最大总温差 36.83 K。何曙等[4]在进口总压为0.4 MPa 时，实验对比了不同流道数目(3～8)下涡流管的性能差异，结果显示流道数为4时，可得到最佳的制冷效应，喷嘴流道数为8 时，其制冷效应最差。汤振豪等[5]研究了喷嘴结构对涡流管性能的影响，结果显示螺旋喷嘴比直流喷嘴涡流管具有更好的能量分离效果。何鹏等[6-7]对大管径八流道直流/螺旋喷嘴涡流管的流动与传热性能进行了分析，结果表明大管径多流道涡流管相较小管径涡流管在天然气处理能力及压降特性上具有明显优势。

小管径涡流管内气体的动量和能量变化有其自身特点，相较于大管径涡流管其结构小巧更便于加工制作。为了进一步强化小管径涡流管的制冷性能，使其更好地应用于油田伴生气的轻烃回收，采用均匀设计方法，选取涡流室直径、热端管长、冷端孔径3个结构参数，结合数值模拟进行优化计算，并对计算结果进行二次多项式逐步回归分析，通过对拟合经验公式寻优，得到优化后的结构参数。

1 数值计算模拟

1.1 小管径涡流管初始结构参数

小管径涡流管内部结构的三维数值模型以及实物构造如图1、图2所示。初始结构涡流管尺寸见表1，数值模型在三维笛卡尔坐标系下搭建，选取z轴作为旋转轴线，冷端出口方向为正方向，热端阀末端截面圆心为原点坐标。

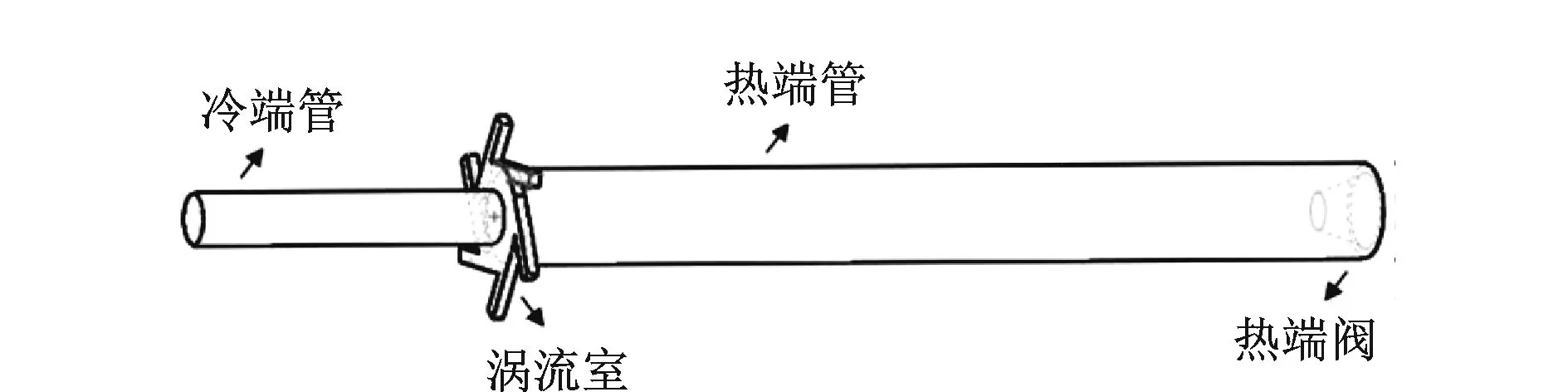
图1 数值计算模型Fig.1 Numerical calculation model

图2 实物效果Fig.2 Physical picture

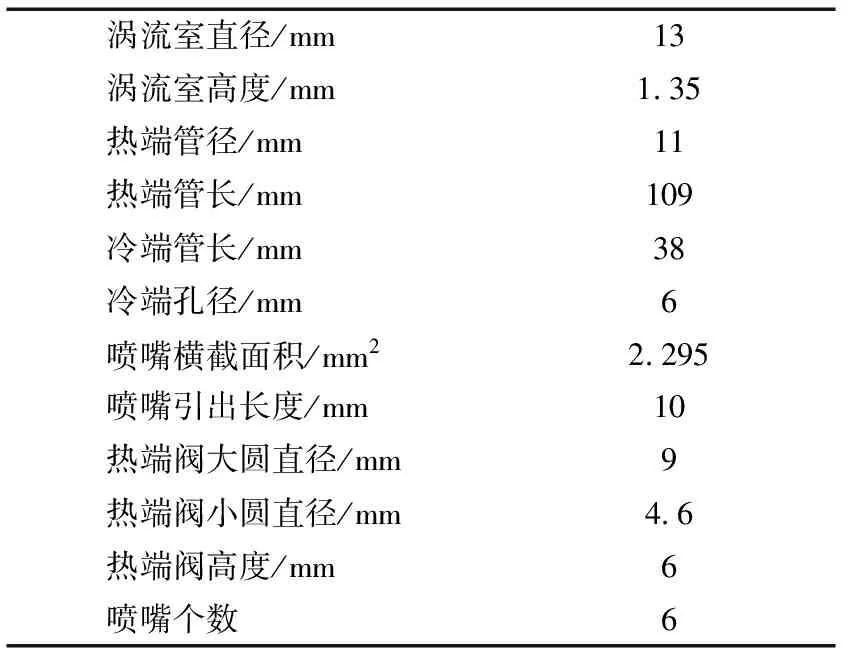
表1 初始结构涡流管尺寸Tab.1 Initial structural parameters of vortex tube

1.2 数值模型和边界条件

小管径涡流管内气体流动规律复杂，进行湍流计算时，需要选取合适的湍流方程。相关研究表明Realizablek-ε湍流模型进行涡流系数计算时引入了与曲率、旋转有关的知识，利用其对涡流管内气体的流动规律进行数学描述比较合理。Realizablek-ε模型的理论计算公式为

(1)

(2)

(3)

式中：ρ、t、μ、μt分别为密度(kg/m3)、时间(s)、动力黏度和湍动黏度(Pa·s)；ui、uj为时均速度，m/s；δij为“kronecker delta”符号；υ为运动黏度与湍流耗散率的乘积，m4/s4；Gk为由平均速度梯度引起的湍动能k的产生项；Gb为浮力引起的湍动能产生项；σk和σε分别为与湍动能k和耗散率ε对应的Prandtl数；C1为时均应变率的函数；C2、C1ε、C3ε为经验常数。

数值模拟时，选取油田伴生气作为理想可压缩气体，伴生气组成见表2。

表2 伴生气组成Tab.2 Composition of associated gas

采用标准壁面函数对数值模型近壁面进行计算。边界类型为压力入口和压力出口，入口总压0.4 MPa，入口总温293 K，冷端出口背压为大气压，调节热端出口背压改变冷流比，通过水力直径和湍流强度设置进出口边界的湍流条件。假设管壁为绝热、无滑移壁面，忽略与外界热和功的交换。

1.3 网格独立性和模型验证

由于数值计算结果受网格节点数影响较大，为保证计算结果的准确性，对数值模型进行网格独立性检验。对比不同网格节点数下初始结构涡流管在冷流比0.71下的制冷温差变化，结果如图3所示。从图3可以看出，当网格节点数目达到455 890时，制冷温差已经趋于稳定，满足网格独立性要求。

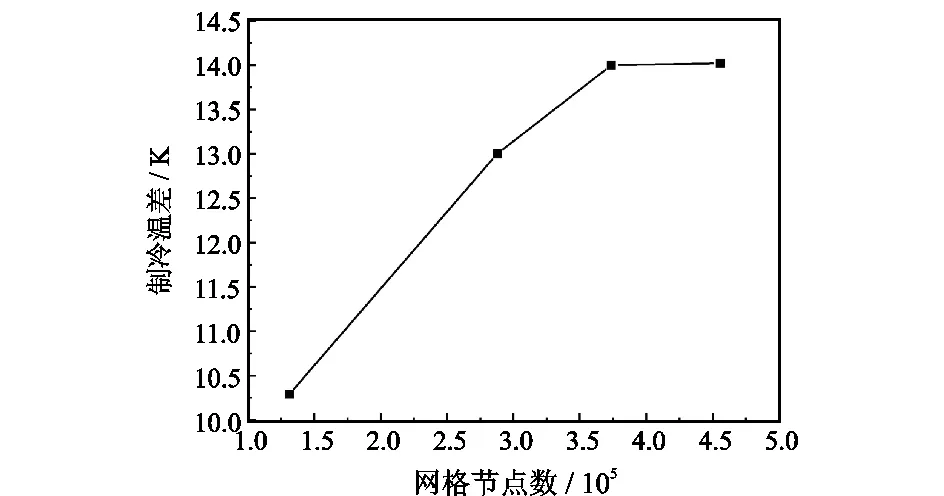
图3 网格节点数与制冷温差的关系Fig.3 Relationship between number of grid nodes and refrigeration temperature difference

为验证模拟结果的可靠性，计算初始结构涡流管在冷流比0.29下，热端管无因次轴向位置z*=0.3截面处无量纲总温的径向分布，并与文献[8]和[9]的实验测量数据进行比对，如图4所示。文献[8]和[9]研究所采用涡流管的结构参数及操作参数见表3。

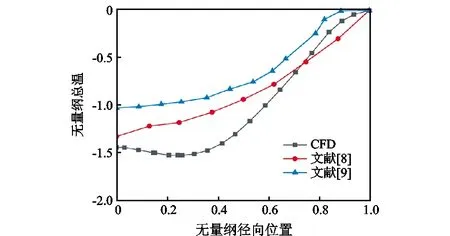
图4 无量纲总温径向分布Fig.4 Radial distribution of dimensionless temperature difference

表3 不同研究者采用涡流管的结构参数及操作条件Tab.3 Structural parameters and operating conditions of vortex tubes used by different researchers

无量纲总温定义为[8-9]

(4)

无量纲径向距离与轴向距离定义为

r*=r/R；

(5)

z*=z/Z。

(6)

式中：Tt为气体的总温，K；Tw，t、Vmax分别为与Tt相同横截面处气体的最大总温(K)、最大速度(m·s-1)；cp为定压比热，J·kg-1·K-1；r、R分别为热端管横截面不同半径位置(mm)、相应的横截面半径(mm)；z、Z为热端管横截面所处位置的热端管长和热端管总长，mm。

由图4可知，尽管不同研究者所采用的涡流管结构以及操作参数有所差异，但其无量纲总温的变化趋势基本一致，因此可证明该模拟结果具有可靠性[10-12]。

2 均匀设计方案

涡流室直径D(X1)、热端管长L(X2)、冷端孔径d(X3)这3个结构参数对小管径涡流管制冷效应影响很大，为了强化小管径涡流管制冷性能，选择以上3个参数进行结构优化设计，同时为利于建模和优化，选用均匀设计表U9(93)进行正交试验，各因素水平取3倍因素数，为获取尽可能多的低温冷流，选取冷流比0.71下的制冷温差ΔT(Y)作为优化评价指标。

具体方案设计及计算结果见表4。

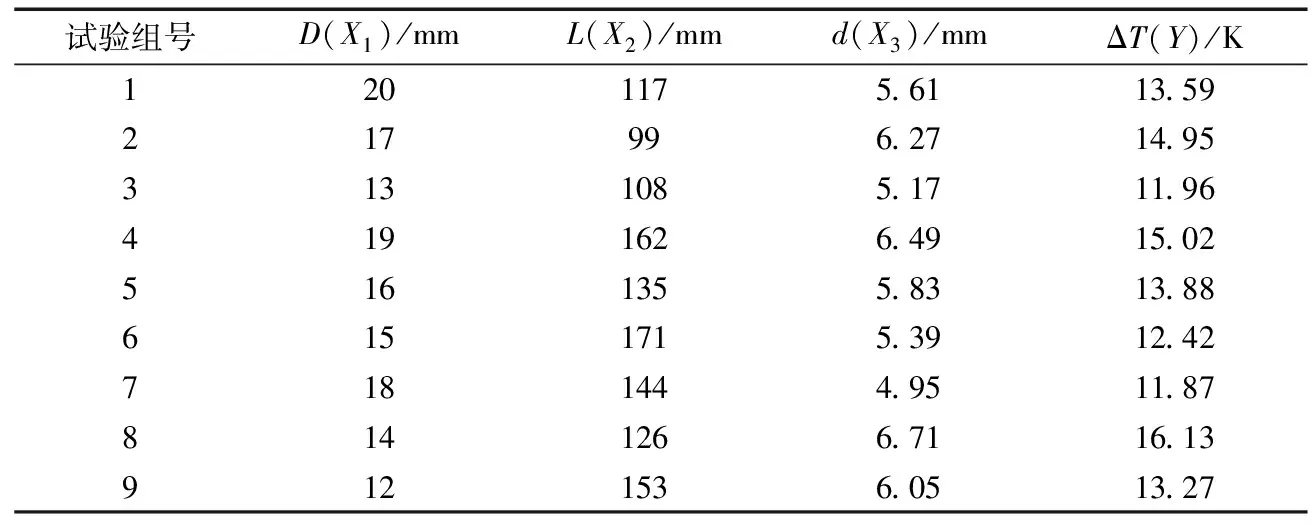
表4 均匀设计方案及结果Tab.4 Uniform design schemes and their results

3 结果分析

3.1 计算结果的回归分析

采用数据回归分析软件对均匀试验计算结果进行二次多项式逐步回归分析，在α=0.05的显著水平下逐步剔除不显著项后拟合得到经验公式

Y=-3.81X1X1-3.21×10-5X2X2+0.30X3X3-0.07X1X3。

(7)

其中，Y为冷流比0.71下小管径涡流管的制冷温差，K；X1为涡流室直径，mm；X2为热端管长，mm；X3为冷端孔径，mm。回归方程的相关系数R=0.994 6，调整后的相关系数Ra=0.985 6，P=0.003 7<0.05，Df(5，3)，F=55.194 2，查询F分布(α=0.05)，F=9.01<55.194 2，表明拟合经验公式回归显著。

将试验结构参数代入式(7)与数值计算结果进行对比，如图5所示。由图5可见，经验公式计算结果与数值计算结果吻合度较高，趋势基本一致。

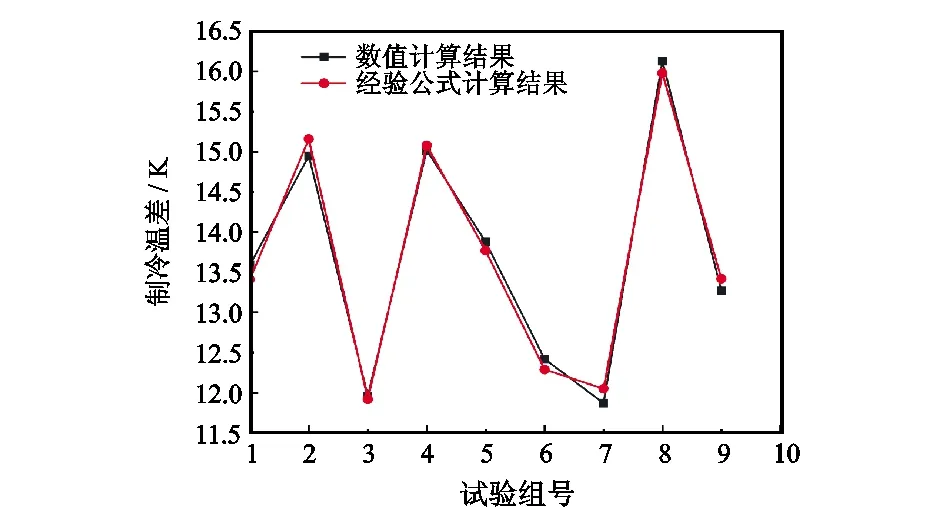
图5 数值计算与经验公式计算对比Fig.5 Comparison of numerical calculation results with empirical formula calculation results

对经验公式进行寻优，同时依据加工精度，将经验公式预测的最优指标圆整为X1=16 mm，X2=127 mm，X3=6.71 mm。

小管径涡流管结构参数优化前后对比见表5。

表5 结构参数优化前后对比Tab.5 Comparison of structure parameters of vortex tube before and after optimization

使用最优指标进行数值建模计算，得到最大制冷温差16.24 K，高于计算得到的初始结构涡流管最大制冷温差 14.02 K，这表明在高冷流比下，适当增大涡流室直径，提高冷端孔径及热端管长能有效提高制冷性能。

3.2 优化结构与初始结构涡流管对比分析

为进一步研究结构优化提升小管径涡流管制冷性能的效果，从涡流管内速度场、温度与压力场以及冷流比3个方面对结构优化的影响进行分析。选取初始结构和优化结构涡流管的涡流室横截面为参考截面。

3.2.1 速度场分布

气体在喷嘴内充分膨胀后，喷入涡流室内作高速旋转运动，气体静压下降，静温降低，静压能转化为动能，为后续能量分离提供了初始动能。切向速度在数量级上要高于轴向与径向速度，一定程度上能反映涡流管内能量分离作用的强弱。切向速度、轴向速度径向分布如图6、图7所示。由图6可知，当冷流比为0.71时，涡流室内切向速度近似呈现“兰金涡”分布，优化结构与初始结构涡流管的最大切向速度均出现在径向位置4.4 mm处，分别达到437 m/s和410 m/s，优化结构涡流管的切向速度更高，更利于能量分离。

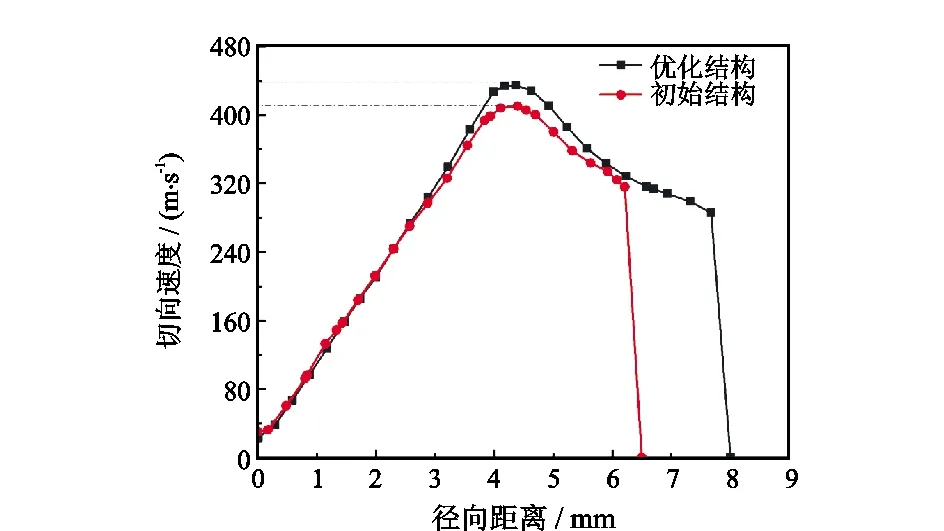
图6 切向速度径向分布Fig.6 Radial distribution of tangential velocity

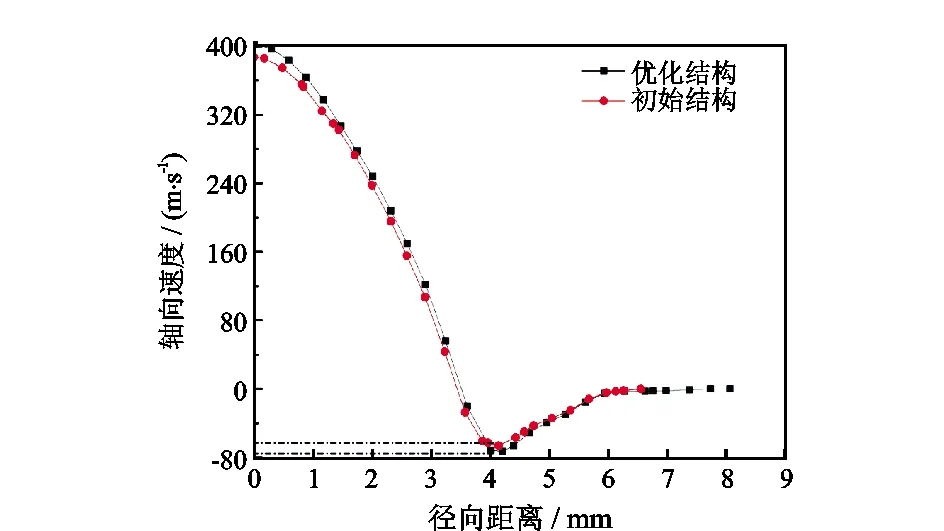
图7 轴向速度径向分布Fig.7 Radial distribution of axial velocity

轴向速度数量级上要小于切向速度，但对小管径涡流管内能量分离存在重要影响，在一定程度上反映冷热分离能力。由图7可知，当冷流比为0.71时，轴向速度存在明显的“零速面”，轴向速度正值代表内旋冷气流，流向冷端出口；轴向速度负值代表外旋热气流，流向热端出口。优化结构涡流管在内、外旋流上的最大轴向速度分别为402 m/s与-73 m/s，初始结构涡流管在内、外旋流上的最大轴向速度分别为387 m/s与-66 m/s，对比可知，结构优化后的小管径涡流管轴向速度提高，冷热分离能力更强。

3.2.2 温度与压力场分布

内、外旋流气体的相互作用致使动能在两者间发生运移，因此气体总温在径向上产生分离，中心区域附近总温较低，近壁处总温较高，如图8所示。由图8可知，优化结构涡流管的内旋冷气流在中心区域附近的最低总温达到270.17 K，而初始结构涡流管的内旋冷气流在中心区域附近的最低总温仅为274.02 K，因此优化结构的总温分离效果更好。

总压分布表征着内、外旋流气体间的能量传递，如图9所示。由图8可知，在径向4.4 mm位置处，总温变化已趋于平缓，表明内、外旋流气体间的相互作用基本结束，能量传递已经完成，因此应该尽量减少总压在径向大于4.4 mm区域内的损失，才能提高涡流管的实际绝热效率。由图9可知，优化结构涡流管在径向大于4.4 mm区域内的总压损为175 93 Pa(压损梯度604 6 Pa/mm)低于初始结构涡流管的总压损191 91 Pa(压损梯度126 26 Pa/mm)，表明优化结构涡流管具有更好的冷热分离效果。

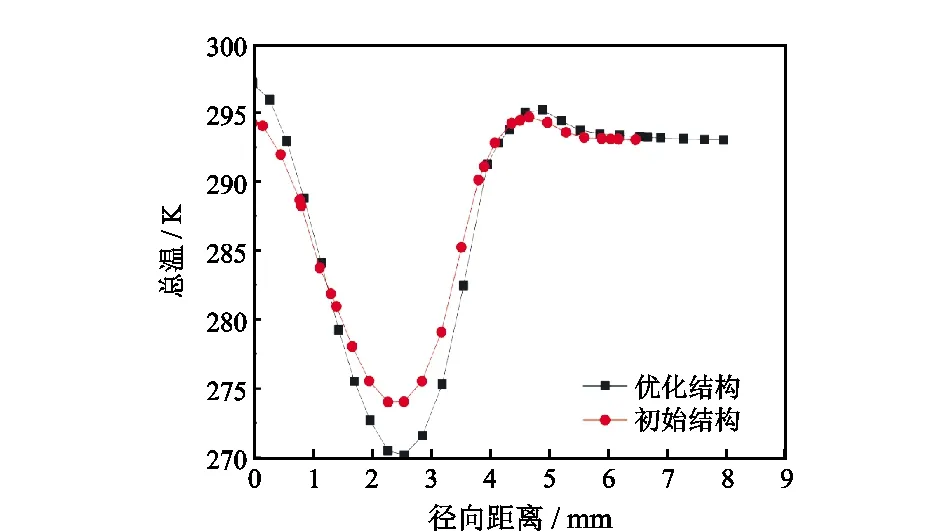
图8 总温径向分布Fig.8 Radial distribution of total temperature

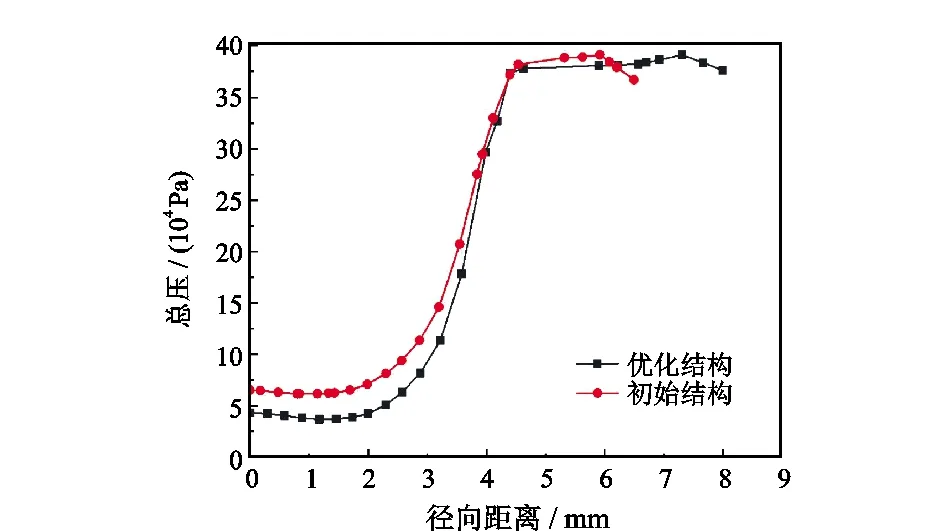
图9 总压径向分布Fig.9 Radial distribution of total pressure

3.2.3 冷流比对结构优化影响分析

小管径涡流管用于油田伴生气轻烃回收时，选择合适的冷流比非常关键。冷流比过低(小于0.2)虽能获得温度较低的冷气流，但冷气流量较小，不利于工业规模处理；冷流比过高(大于0.8)能获得较大冷气流量，但温降较低，加大了后续深冷负荷。为尽量获取更多低温冷气流同时避免温降幅度过小，选取冷流比在0.71～0.79。为了进一步分析结构优化对涡流管制冷性能的影响，对比优化结构与初始结构涡流管在冷流比0.71～0.79范围内制冷温差与单位制冷量的数值变化。制冷温差(入口总温减去冷端出口总温)为ΔTc，单位制冷量(每kg气体获得的冷量)为qc，表达式为

ΔTc=Ti-Tc，

(8)

qc=γcp(Ti-Tc)。

(9)

式中：γ为冷流比；cp为定压比热容，J·kg-1·K-1；Ti为入口总温，K；Tc为冷端出口总温，K。

制冷温差、单位制冷量随冷流比变化如图10、图11所示。由图10可知，冷流比在0.71～0.79范围内变化，小管径涡流管的制冷温差随冷流比增大而逐渐减小，这是因为随冷流比增大，更多的近壁高温气流从冷端出口流出，提高了冷端气流的出口总温，并且可以看到，在同一冷流比下优化结构涡流管的制冷温差明显高于初始结构涡流管的制冷温差，在冷流比为0.71时，两者的制冷温差最大，分别为16.24 K与14.02 K，冷流比为0.79时，两者的制冷温差最小，分别为11.79 K与9.79 K。

图10 制冷温差随冷流比变化Fig.10 Refrigeration temperature difference changing with cold flow ratio

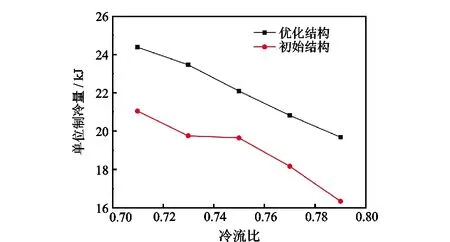
图11 单位制冷量随冷流比变化Fig.11 Unit cooling capacity changing with cold flow ratio

由图11可知，冷流比在0.71～0.79范围内变化，小管径涡流管的单位制冷量变化趋势与制冷温差一致，并且可以看到，在同一冷流比下优化结构涡流管的单位制冷量显著高于初始结构涡流管，在冷流比为0.71时，两者的单位制冷量最大，分别为24.38 kJ与21.05 kJ，冷流比为0.79时，两者的单位制冷量最小，分别为19.69 kJ与16.35 kJ。

4 结 论

(1)采用均匀设计安排数值计算试验方案，对小管径涡流管进行了结构优化计算，并对计算结果进行了回归分析，通过对拟合经验公式寻优，得到了优化后的结构参数。优化结构涡流管在入口总压0.4 MPa、入口总温293 K、冷流比0.71下的制冷温差与单位制冷量相比初始结构涡流管分别提高2.22 K与3.33 kJ。

(2)对比优化结构与初始结构涡流管内部速度场、温度与压力场分布可以发现，优化结构涡流管在切向速度、轴向速度、总温与总压分布上均体现出更加良好的冷热分离性能。

(3)对比分析了冷流比0.71～0.79条件下，优化结构与初始结构涡流管的制冷温差与单位制冷量，结果表明优化结构涡流管的制冷温差与单位制冷量均明显高于初始结构涡流管。