汶川地震失稳机制的数值模拟研究

李平恩，廖力，奉建州

1 中国地震局地球物理研究所，北京 100081 2 北京白家疃国家地球科学野外科学观测研究站，北京 100095

0 引言

强烈地震是一种严重的自然灾害，给生命财产造成巨大损失.地震学家很早就认识到，大陆构造地震是断层和围岩系统在构造作用下的一种力学失稳过程(Nur, 1978; Rice, 1979; Stuart, 1979a)，其中，断层的软化特性是造成地震失稳的最重要原因(殷有泉和张宏，1984; Reches and Lockner, 2010).研究断层地震的孕育发生过程必须考虑包含断层和围岩在内的整个岩石力学系统.Stuart(1979a)首先提出用准静态力学方法研究地震不稳定性，并通过建立一个考虑应变软化不稳定性的平面理论模型研究了1971年美国加州San Fernando 6.4级逆冲地震(Stuart, 1979b)，计算得到的震前和震后的地表抬升量与观测资料吻合较好.在研究中，断层软化本构规律可采用在峰值应力后的应变软化或应变率软化形式，以及应力-滑动或应力-滑动率的摩擦规律来表示(Stuart and Mavko, 1979; Rice, 1983).考虑到Stuart(1979b)提出的应变软化本构方程与空间坐标有关，不符合本构性质的客观性原理，在理论上有瑕疵.殷有泉和张宏(1982，1984)建立了严谨的应变软化的断层面本构关系，用间断面单元模拟断层，在此基础上给出了地震非稳定模型的一般数学表述，并从理论上指出地震失稳发生在峰值应力之后.当断层本构关系的软化行为采用理想化的速率无关的滑移弱化或速率状态相关的摩擦关系进行描述时，地震失稳的位移应力曲线(Rudnicki,1988)形态与殷有泉和张宏(1984)的结果完全一致.这从理论上进一步肯定了断层本构的软化特性是导致地震失稳的必要条件，它与本构关系的具体描述形式无关.最近，李平恩和殷有泉(2009，2014)采用稳定性理论进一步讨论了直立走滑型和倾斜逆冲型断层地震的失稳机制，其中断层软化本构关系采用理论推导的负指数形式的软化模式，它假设断层局部微元强度遵循Weibull概率分布，采用统计力学方法推导得到宏观本构关系.研究表明，当围岩切线刚度小于断层峰后软化阶段切线刚度绝对值的最大值时，整个系统的切线刚度为负，会发生地震失稳，且伴随应力突跳和围岩应变能释放，其余情况仅仅是断层无震滑动，不会发生地震.

以上理论模型均为单自由度问题，接近实际情况的地震模型都是多自由度的，需要采用数值方法进行模拟研究.王连捷等(2009，2011)将围岩看作弹性体，断层看成具有应变软化特性的弹塑性体，断层和围岩组成统一的地质介质系统，采用有限差分FLAC-3D软件分别模拟了汶川MS8.0地震以及玉树MS7.1地震的发震过程，计算了应力降、能量释放量、断层错动量、同震位移、震前位移、地震复发周期等重要参数，结果与野外调查资料具有较好的一致性.由于问题的复杂性，研究中所建立的数值模型均是高度简化和概念性的.

2008年5月12日汶川MS8.0地震发生在青藏高原东缘的龙门山断裂带上，其发震动力学机制引起广泛关注.龙门山断裂带在汶川地震前并没有7.0级以上地震记录(邓起东等，2011; Ran et al., 2013).震前GPS观测和地震地质研究结果都表明龙门山断裂带自晚更新世以来具有比较弱的活动性(Gan et al., 2007)，横跨整个断裂带的滑动速率不超过2 mm·a-1，单条断裂的滑动速率只有不到1 mm·a-1(张培震等，2008).汶川震后，科学家从构造变形和地震地质、数值模拟等不同角度对汶川地震的发震机制进行研究.张培震等(2009，2012)提出了汶川地震的多单元组合模式，认为地震的孕育和发生是川西高原变形单元、龙门山断裂带闭锁单元和四川盆地支撑单元共同作用的结果.张竹琪等(2010)的研究结果显示龙门山断裂带深部缓倾角、浅部高倾角逆冲断层结构对汶川地震有促进作用.深部结构探测的结果表明汶川地震初始破裂段上地壳呈现高速异常，并且速度结构和物性结构差异是控制地震破裂分布的主要因素(邓文泽等，2014).朱守彪和张培震(2009)、Zhu和Zhang(2010)、陈棋福等(2015)、马林飞等(2018)采用数值模拟方法，通过建立横跨龙门山断裂带的二维平面应变模型，研究了汶川地震的动力学机制，讨论了摩擦系数和断层倾角等对地震发生的影响.他们在研究中均采用速率-状态相依的摩擦本构关系模拟断层面上的摩擦机制.

因此，考虑到断层的软化特性对地震失稳的重要性，本文通过建立横跨龙门山断裂带并包含川西高原和四川盆地在内的汶川二维平面地震力学模型，采用有限元方法数值计算得到了包含断层和围岩在内的整个岩石力学系统的平衡路径曲线.从地震不稳定性角度详细探讨了汶川地震的孕育发生过程和失稳机制，分析了断层倾角以及断层材料参数对系统稳定性状态和地震失稳过程的影响.

1 汶川地震不稳定性模型

1.1 模型的建立

汶川地震发生在龙门山断裂带中段，震中位于映秀镇西南，同震破裂沿中央断裂和前山断裂以朝北东方向破裂为主(邓起东等，2011).在地震震源破裂过程中，南段以逆冲为主，向北逐渐转变为以走滑为主.如图1所示，取垂直于龙门山断裂带并过汶川地震初始破裂点的剖面建立模型.由于剖面所在断裂的同震破裂主要由垂直于断层走向的水平挤压导致，平面应变假设可近似成立(马林飞等，2018).

图1 汶川地震构造背景及模型剖面位置

过图1中剖面建立垂直于龙门山断裂带，包含川西高原和四川盆地在内的汶川地震不稳定性二维平面应变地震力学模型，如图2所示.模型取从地表到Moho面深度的纵剖面，四川盆地与川西高原以龙门山断裂带为界.龙门山断层带、川西高原和四川盆地共同组成统一的断层围岩岩石力学系统.川西高原地形高度取为4 km，四川盆地地形高度取500 m，龙门山断裂带高度取为3 km，向东逐渐降低，10 km后降到四川盆地高度.龙门山断裂带两盘在地表位置的川西高原一侧为点A，四川盆地一侧为点A′.模型右侧的四川盆地Moho面深度取为40 km，上地壳厚度取为22.5 km；左侧的川西高原Moho面深度为70 km，上地壳和下地壳厚度分别为26 km和48 km.考虑到四川盆地所在的华南地块相对川西高原运动速度很低，可视为固定不动，川西高原一侧受构造加载的推挤作用.因此，在图2右端面和四川盆地Moho面取法向约束，在川西高原左端面施加远场位移a，Moho面取自由边界.这样的边界条件模拟了下地壳物质向上运动的趋势，有利于断层解锁.

图2 汶川地震不稳定性地震力学模型示意图

考虑到龙门山断裂带在空间几何结构上具有高角度铲形结构特性，浅地表倾角达60°～70°，甚至更陡(张培震等，2008)，因此在模型中将其设置成一条浅部高倾角、深部低倾角的铲形断层.为研究断层倾角变化对汶川地震失稳的影响，设置了龙门山断裂带深浅部倾角不同的3组模型，几何参数见表1所示.3组有限元模型如图3所示.

表1 3组模型中龙门山断裂带几何参数

图3 龙门山断裂带深浅部不同倾角的3组有限元模型

1.2 本构关系和材料参数

岩石圈介质在漫长的地质演化历史中具有流变性质，而在地震发生瞬时，则表现为弹性性质，本文采用Maxwell黏弹性本构模型模拟岩石圈介质在不同时间尺度的力学性质，本构关系为

(1)

其中，K(t)和G(t)分别为Maxwell模型的体积模量和剪切模量，η为黏滞系数，K和G分别为弹性体积模量和弹性介质模量，可以由线弹性介质的杨氏模量E和泊松比ν换算得到(王敏中等，2011).E和ν可根据研究区深部反演得到的三维P波、S波速度模型和密度模型计算得到(李平恩等，2019).地震波速结构(Li et al., 2013)和岩石圈三维流变结构反演结果(孙玉军等，2013)显示，相比青藏高原东部的川西高原地区，四川盆地的地壳介质较为坚硬，弹性模量更大，黏滞系数更高.综合以上结果并参考其他学者的模型参数取值(朱守彪和张培震，2009；陈棋福等，2015；刘盼等，2017；马林飞等，2018)，计算中模型材料参数见表2，地壳泊松比统一取为0.25.

表2 模型中川西高原和四川盆地分层材料参数

研究中考虑断层的软化特性，并且注意到远场刚施加位移载荷a时，断层并没有错动，只有当断层受力达到足够大数值时才会发生破裂，因此取龙门山断裂带具有初始破裂强度，只有当断层面内剪应力τf达到一定数值时断层才发生破裂进而开始错动.断层破裂面通常是压剪性破裂，一般采用具有压力相关性的Coulomb型破裂准则，它的剪切强度是

τf=c-μσn=c+μ|σn|,

(2)

式中σn是垂直断层面的正压力，按弹性力学约定，以拉应力为正，因此正压力本身取负值.μ和c是断层的材料参数，分别称为断层面的内摩擦系数和黏聚力，且有关系φ=arctanμ，φ是内摩擦角.如果断层面内剪应力用τ表示，那么断层的破裂准则为

f=τ-τf=τ-c+μσn=0,

(3)

它是一个双参数(c和μ)的破裂准则.将断层两盘切向相对位移称为断层错距u，为研究断层的稳定性，至少需要假设一个强度参数(c或者μ)是断层错距u的减函数，可采用负指数形式的软化模式(李平恩和殷有泉，2014)

(4)

或

(5)

式中c0和μ0分别是断层的初始(当u=0时)黏聚力和内摩擦系数，m是强度曲线的形状参数，有m≥1，u0是平均错距的一种度量.由于u0的选取也能反映强度曲线的形状，称其为曲线的“胖度”(李平恩和殷有泉，2009).为研究的方便，同时取c和μ分别为如式(4)和式(5)所示的软化模式，因此，描述断层软化特性的参数共有4个，分别是c0、μ0、u0和m.以大型通用有限元计算程序ADINA为计算平台，采用二次开发技术开发了断层软化本构模块.断层采用间断面单元进行模拟，除断层外的其他介质采用Maxwell黏弹性本构模型描述.远场加载速度取为2 mm·a-1，总加载量a等于加载速度乘以按年计算的加载时间，总加载时间取2000年.

2 地震不稳定性分析

在以上模型参数和加载条件下，给定不同的断层软化参数，可以计算得到远场位移a与四川盆地一侧右端面约束反力P的关系，它们在能量上是共轭的.对于包含断层和围岩在内的整个岩石力学系统，可以将a看作是输入的控制变量，P是系统的响应.在以a为横轴，P为纵轴的坐标平面内，每一个点(a,P)代表一个平衡状态，整个a-P曲线代表所有的平衡状态，称为平衡路径曲线，可以用来研究整个系统的稳定性(李平恩和殷有泉，2014).下面具体讨论断层倾角和断层软化参数对地震不稳定性的影响.

2.1 初始内摩擦系数的影响

为分析断层初始内摩擦系数对地震失稳的影响，对于模型1，取c0=5000 Pa，u0=0.7 m，m=2时，分别计算了初始内摩擦角φ0=arctanμ0取不同值时的平衡路径曲线，如图4所示.为分析地震从孕育到发生过程中断层两盘的垂直位移变化特征，同时给出了龙门山断裂带两盘地表处(川西高原一侧为点A，四川盆地一侧为点A′，如图2所示)垂直位移随时间的变化曲线，如图5所示.由图4可知，当初始内摩擦角为23°时，从平衡路径曲线来看，随远场位移a的增加，约束反力P也缓慢变化，没有发生突跳，表明断层处于缓慢无震滑动状态，没有地震失稳发生.平衡路径曲线有4个关键点，即C、E、F和G点，它们将平衡路径曲线分成不同的段，各段对应的断层运动状态、应力和应变能变化特征不同.结合图5可知，在点C之前，断层上下盘垂向位移增速缓慢且增速相同，表明断层处于闭锁状态，系统处于整体加载状态，约束反力P随远场位移a不断增大.随远场位移a继续增加，在点C开始，断层上盘垂直位移增速明显加快，表明断层克服闭锁状态开始启动并缓慢无震滑动.在平衡路径曲线应力峰值点E之前的CE段，约束反力P继续增加，但增速明显降低，表明在断层缓慢无震滑动过程中储存的应变能开始不断释放，使得应力增速降低，但释放的应变能速度小于远场位移加载增加的应变能速度，因此系统总应变能和应力是持续增加的.峰值应力点E也是平衡路径曲线的转向点，在转向点E之后的EFG段，约束反力P开始降低，表明其间应变能释放速度大于远场位移加载增加应变能的速度，因此系统总应变能和应力持续减小.在E点之前，断层上下盘垂直位移方向相同，均是垂直向上.过E点后，断层下盘垂直位移开始变为垂直向下运动，断层上下两盘垂直运动方向相反.点F将EFG段进一步分为EF段和FG段两部分.在EF段，应力和断层两盘垂直位移变化速率相对较缓，表明在该阶段应变能释放速度相对较慢.而在过点F之后的FG段，应力减小速度和断层上盘垂直位移增加速度先显著加快后逐渐变慢，表明应变能释放速度先明显加快后逐渐变慢，断层无震滑动速度也先明显加快后逐渐变慢.最后，在点G，约束反力P开始由减小状态重新转变为增加状态，断层上盘垂直位移增速降低，断层下盘开始逐渐重新转变为垂直向上运动.过点G后，系统应力和总应变能又开始增加，断层上盘或下盘的垂直位移增速逐渐趋于一个稳定值，断层进入匀速缓慢无震滑动状态.

由图4和图5a可知，随着初始内摩擦角从23°增大到30°，初始内摩擦系数增大，断层面摩擦系数越大，断层逐渐由缓慢无震滑动状态转变为闭锁状态.在此情况下，随着远场位移的不断增加，断层面内的剪应力越来越大，最终超过克服断层闭锁状态所需的临界剪应力，导致断层突然错动，伴随应力突跳，系统失稳从而发生地震.当内摩擦角为30°时，从系统平衡路径曲线来看，D是应力峰值点，即力的转向点.在该点之前，系统的状态是稳定的.D也是断层启动点，超过此点，断层错动加速，最终在A点失稳，同时地震发生.在A点失稳时，应力由A点突跳到B点，伴随应力降、断层错距和应变能的急剧释放.在失稳前的DA段，断层错动加速，应力开始降低，应变能开始释放，是失稳的前兆.在失稳临界点A之前，属于地震孕育阶段，其间围岩应变能大量储集，变形是渐变的.在临界点A发生失稳时，系统的应力、断层位错和能量均发生突变.这反映了地震从孕育到发生是一个从渐变到突变的物理过程.地震失稳后过B点，应力和应变能又开始增加，断层逐渐进入震后无震匀速缓慢滑动状态.随着初始内摩擦角从30°增加到35°，初始内摩擦系数进一步增大，地震失稳时对应的远场位移更大，应力降和断层错距更大，体现出克服断层闭锁状态需要的临界剪应力更大，对应失稳时释放的应变能更多，地震的震级更高.

图4 初始内摩擦角取不同值时的平衡路径曲线

图5 初始内摩擦角取不同值时龙门山断裂带两盘地表处垂直位移随时间的变化

由图5可知，对于初始内摩擦角为23°时的无震滑动状态，上盘和下盘的垂直位移变化特征有所不同.具体是，在点C之前，断层处于闭锁状态，上下盘垂直位移方向一致，均是垂直向上增加，且速率相等.在断层克服闭锁状态开始无震滑动的CE段，上盘垂直位移增速相比闭锁状态时是增加的，而下盘虽然垂直位移增速相比闭锁状态时减小，但总的垂直位移仍然是增加的，表明在此阶段，上下盘之间的黏结作用导致断层两盘垂直位移方向仍然保持一致，整体均处于垂直向上运动的状态.过转向点E之后，随着应变能的加速释放，上下盘之间的黏结作用降低，上盘和下盘的垂直运动方向开始反向，表现为上盘垂直向上运动，下盘垂直向下运动.过点G后，应力和应变能又开始增加，断层上盘垂直位移增速逐渐降低并趋于稳定，断层下盘由垂直向下运动逐渐转变为垂直向上缓慢匀速运动，上下盘的垂直运动方向均为垂直向上，趋于一致.最后断层保持缓慢匀速滑动.对于初始内摩擦角为30°时的地震失稳状态，断层两盘在峰值应力点D之前一直处于闭锁状态，两盘的垂直位移增速相同，方向垂直向上.过D点后，断层克服闭锁状态开始启动，并且加速错动，断层上下两盘的垂直运动方向相反，上盘垂直向上、下盘垂直向下运动.最后，断层两盘垂直位移在失稳点A发生突跳，上盘川西高原一侧垂直向上，下盘四川盆地一侧垂直向下，体现出逆冲地震的特征，上盘垂直位移变化量明显高于下盘.地震失稳后，断层上盘很快恢复到垂直向上匀速运动状态，断层下盘也由垂直向下运动逐渐转变到垂直向上匀速运动状态，断层进入震后缓慢匀速无震滑动状态.随着初始内摩擦角进一步增加，地震失稳突跳的时间延后，失稳时断层错距增大，失稳前的断层加速错动阶段变短.由图4和图5进一步可知，初始内摩擦系数变化时，系统无论是断层缓慢无震滑动状态还是地震失稳状态，系统重新进入应力和应变能增加状态后，约束反力P随远场位移a的增速是一致的，并且断层上盘或下盘的垂直位移增速也是一致的.

根据前述分析，汶川地震从孕育到发生的过程与图4和图5中对应的不稳定的地震失稳情况是相同的，考虑到其震级达到MS8.0，龙门山断裂带初始内摩擦系数可能较大.

2.2 断裂带倾角的影响

为分析龙门山断裂带深浅部倾角对地震失稳的影响，计算参数取c0=5000 Pa，u0=0.7 m，m=2，φ0=15°时，给出模型1至模型3的平衡路径曲线，如图6所示.由图可知，当断层深浅部总体平均倾角由50°增加到70°时，系统逐渐由稳定的无震滑动状态转变为地震失稳状态，并且地震失稳时对应的远场位移比无震滑动时断层启动点对应的远场位移更大.表明在相同的孕震条件下，断层倾角越大，越具备发生地震的条件，但需要更长的孕震时间；倾角越小，围岩储存的应变能通过断层无震滑动的方式释放掉，不容易发生地震.对于断层无震滑动或地震失稳情况，系统重新进入应力和应变能增加状态后，约束反力P随远场位移a的增速是不同的，与断层倾角有关，总体而言，倾角越大，约束反力P随远场位移a的增速越大.

图6 龙门山断裂带深浅部倾角取不同值时的平衡路径曲线

当发生地震失稳时，为研究断裂带倾角的影响，取计算参数c0=10000 Pa，u0=0.7 m，m=2，φ0=45°时，给出模型1至模型3的平衡路径曲线，如图7所示.由图可知，当断层深浅部总体平均倾角由50°增加到70°时，失稳时对应的远场位移增大，表明克服断层闭锁状态需要的临界剪应力更大，孕震时间更长；但突跳时的应力降先增加再减小.图8给出了断层两盘地表处垂直位移随时间的变化.由图可知，断层倾角越大，地震失稳发生的时间越晚.随断层倾角增加，对于断层上盘，地震失稳时垂直位移变化量越大；对于断层下盘，地震失稳时垂直位移变化量先减小再增大.断层倾角越大，地震失稳时断层错距越大.地震失稳断层进入缓慢匀速无震滑动状态后，应力增速以及断层上盘或下盘的垂直位移增速与断层倾角有关，总体而言，断层倾角越大，应力增速以及断层两盘垂直位移增速也稍大.

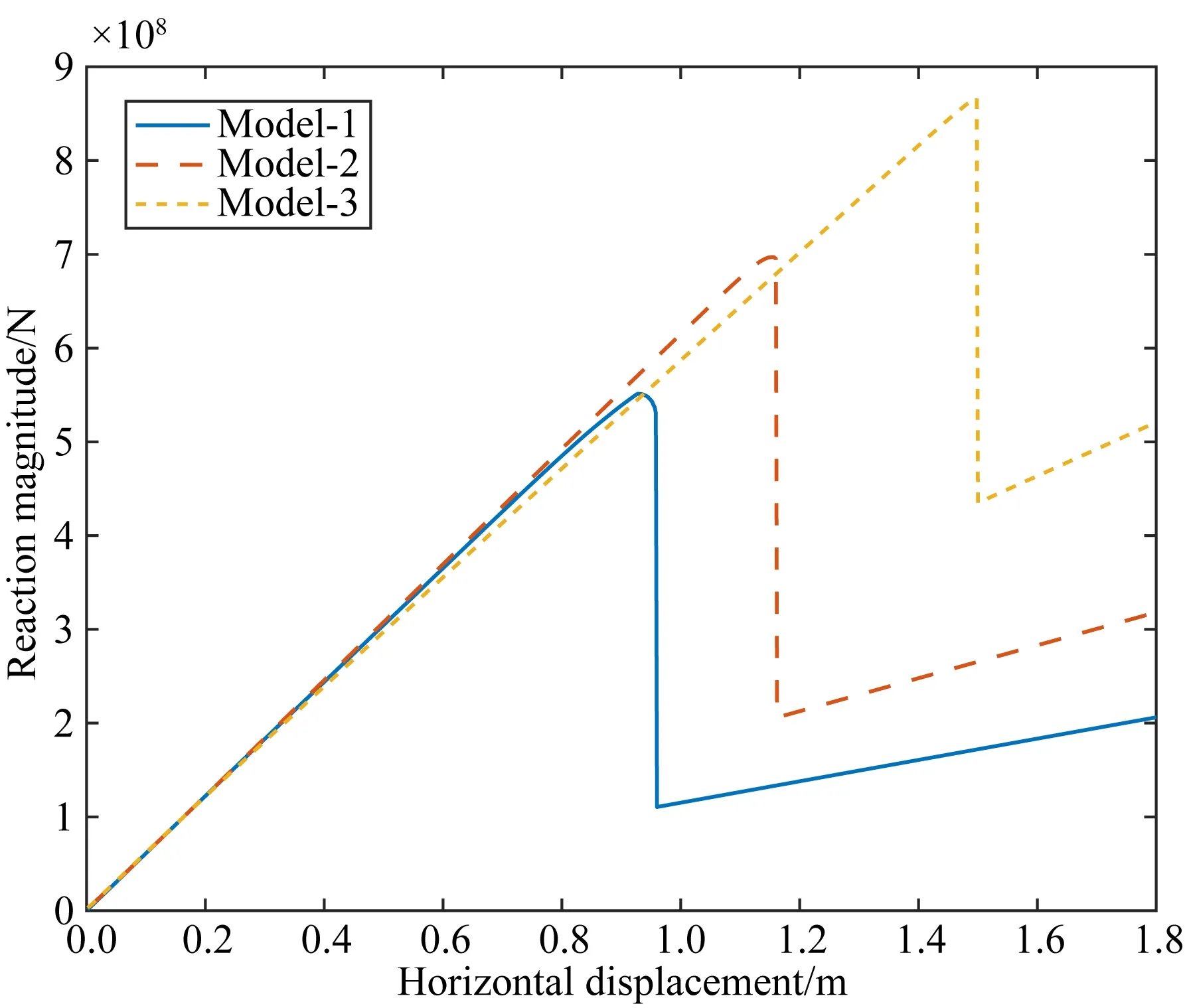
图7 当地震失稳时龙门山断裂带深浅部倾角取不同值时的平衡路径曲线

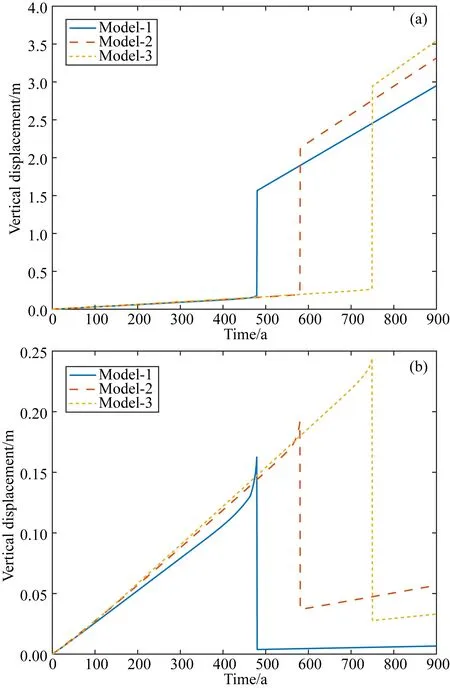
图8 当地震失稳时龙门山断裂带深浅部倾角取不同值时断层两盘地表处垂直位移随时间的变化

2.3 初始黏聚力的影响

为分析断层初始黏聚力对地震失稳的影响，对于模型1，取计算参数为u0=0.7 m，m=2，φ0=25°时，分别计算了初始黏聚力c0取不同值时的平衡路径曲线，如图9所示.由图可知，当初始黏聚力增加时，断层逐渐从稳定的缓慢无震滑动状态转变到失稳状态.并且初始黏聚力越大，地震失稳突跳时对应的远场位移越大，应力降也越大.这表明断层初始黏聚力越大，断层更容易处于闭锁状态，闭锁时间越长，克服闭锁状态需要的剪应力也越大.在断层闭锁期间，随远场位移的增加，断层附近围岩持续变形，将有利于积累更多的应变能.当断层面内剪应力超过克服闭锁状态需要的临界剪应力时，围岩储存的大量应变能容易在极短的时间内得到释放，伴随应力降和断层突然错动，导致地震发生.初始黏聚力越小，断层克服闭锁状态需要的剪应力越小，断层容易滑动，这导致断层附近围岩不容易发生持续变形，进而积累更多的应变能.围岩存储的应变能更容易在断层缓慢无震滑动中释放掉，不会发生地震.对于汶川MS8.0特大地震而言，断层的初始黏聚力可能非常大，这样导致地震的孕育时间非常长，能积累极大的应变能.

图9 初始黏聚力取不同值时的平衡路径曲线

2.4 强度曲线胖度参数的影响

为分析强度曲线胖度参数对地震失稳的影响，对于模型1，取计算参数为c0=5000 Pa，m=2，φ0=25°时，分别计算了胖度参数u0取不同值时的平衡路径曲线，如图10所示.图11给出胖度参数取不同值时的断层两盘地表处垂直位移随时间的变化.由图10可知，胖度参数增加时，断层从不稳定的失稳状态逐渐转变到稳定的无震滑动状态，并且断层无震滑动的启动点对应的远场位移增大.表明胖度参数增大会导致断层趋于无震滑动.由图10和图11可知，尽管胖度参数越小，越容易发生地震失稳，但断层闭锁状态的时间也越短，失稳点越提前，地震发生时的应力降和断层错距越小，释放的应变能也越小，相应的孕震时间也越短.考虑到汶川地震的震级达到MS8.0，不同研究结果均显示其复发周期长达千年量级(张培震等，2008；朱守彪和张培震，2009)，因此龙门山断裂带的胖度参数可能较大.

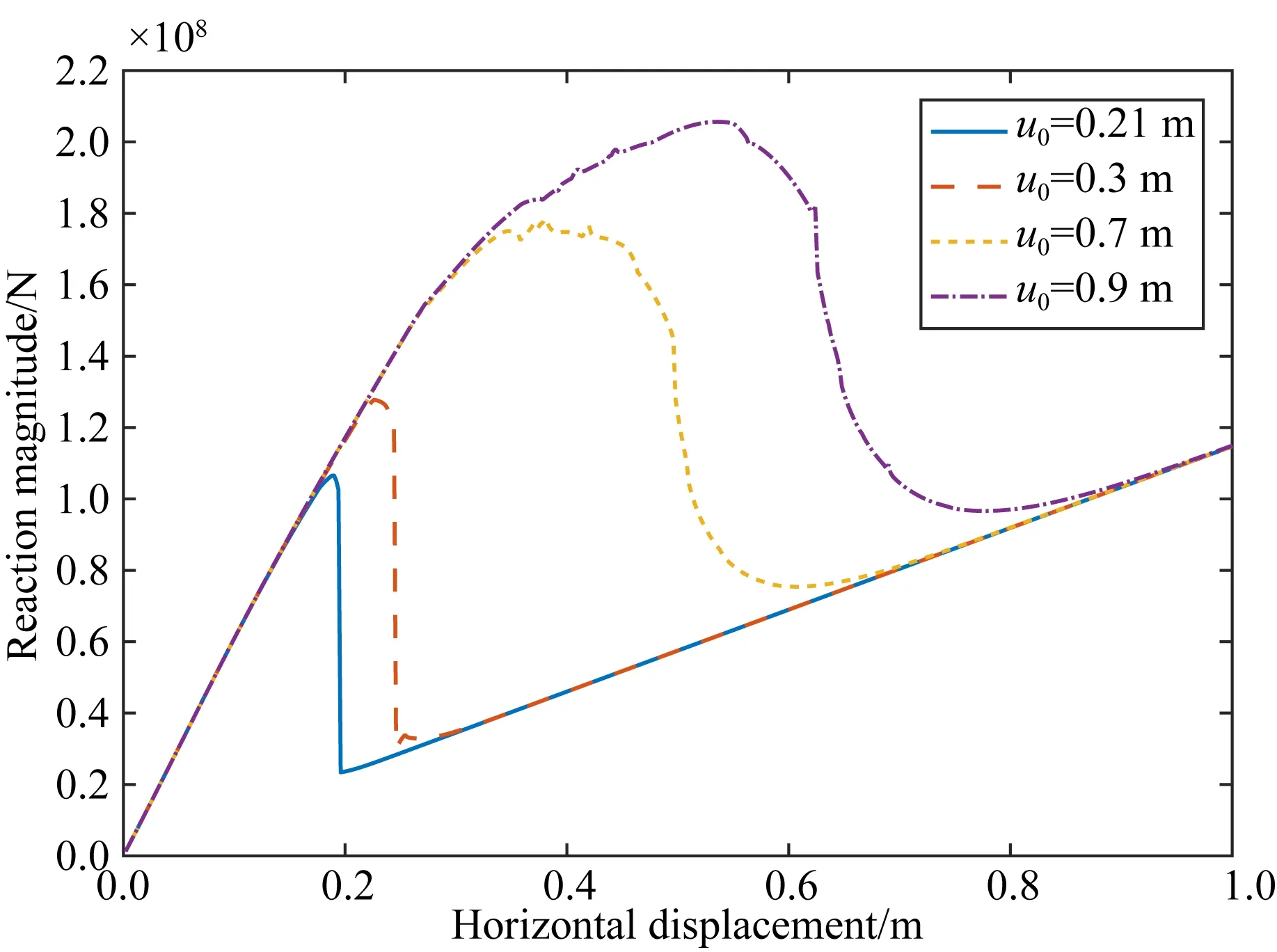
图10 强度曲线胖度参数取不同值时的平衡路径曲线

图11 强度曲线胖度参数取不同值时龙门山断裂带两盘地表处垂直位移随时间的变化

2.5 强度曲线形状参数的影响

为分析强度曲线形状参数对地震失稳的影响，对于模型1，取计算参数为c0=5000 Pa，u0=0.7 m，φ0=25°时，分别计算了形状参数m取不同值时的平衡路径曲线，如图12所示.由图可知，随着形状参数从1增加到7，断层从稳定的缓慢无震滑动状态逐渐转变到不稳定的失稳状态.当发生地震失稳时，随形状参数增大，失稳点对应的时间和地震发生时的应力降也有所增加，但增加量逐渐减小.形状参数m越大，材料脆性越大，当m趋于无穷大时，对应理想脆性材料(李平恩和殷有泉，2009).因此，当m增大到一定值时，继续增加m值，地震失稳时对应的时间和应力降不再发生显著变化，如图12所示.

图12 强度曲线形状参数取不同值时的平衡路径曲线

3 讨论

考虑断层的软化特性时，断层倾角以及断层材料参数对地震稳定性均有影响.当这些参数变化时，整个岩石力学系统会表现为稳定和不稳定2种不同状态.

对于稳定状态情况，如图4至图5，断层初始处于闭锁状态，随着远场位移的增大，断层会克服闭锁状态开始缓慢无震滑动，其间围岩中储存的应变能会不断释放，但释放的应变能速度小于远场位移加载增加的应变能速度，因此虽然应力增速降低，但应力是增加的，系统总应变能也是增加的.当达到应力峰值点之后，断层无震滑动速度逐渐加快，应变能释放速度也逐渐增大，且应变能释放速度超过远场加载增加的应变能速度，系统总应变能不断减少，应力也不断降低，表明存储的应变能通过断层无震滑动的方式快速释放，这个能量大部分转化为断层摩擦滑动产生的热.随着应变能的不断释放，应力减小速度和断层滑动速度不断降低.最后，在远场位移作用下，应力和总应变能又开始匀速增加，断层进入缓慢匀速无震滑动状态.

对于不稳定状态情况，如图4至图5，初始断层一直处于闭锁状态，当达到应力峰值点之后，断层开始克服闭锁状态启动，并且错动加速，应力开始降低，应变能开始释放.应力峰值点是应力增加和减小的分界点，过该点后，随着断层错动加速，最终在失稳点发生地震，储存在围岩中的应变能在极短的时间内急剧释放，同时发生应力突跳，伴随应力降和断层突然错动产生断层错距.在失稳点之前属于地震孕育阶段，应力、变形和应变能的变化是渐变的.在失稳点发生地震失稳时，应力、变形和应变能的变化是突变的，是地震的发生阶段.系统稳定性分析充分反映了地震从孕育到发生是一种从渐变到突变的物理过程.地震发生后，应力和总应变能又开始增加，断层进入震后缓慢无震匀速滑动状态.研究得到一个地震周期内整个岩石力学系统的应变能从积累到突然释放的全过程，与马林飞等(2018)采用速率-状态相依断层摩擦本构的模拟结果吻合.

对于地震失稳情况的平衡路径曲线，在应力峰值点和失稳点之间是断层错动加速阶段，是失稳的前兆，其间应力开始连续降低，应变能开始连续释放.断层倾角和断层材料参数取不同值时的计算结果显示，在大部分情况下，该阶段存在的时间是短暂的，在有些情况下应力峰值点和失稳点非常接近，这表明断层刚克服闭锁状态进入加速错动阶段后就很快发生地震失稳，导致失稳前兆的存在时间异常短暂.

当断层材料参数，即初始内摩擦系数、初始黏聚力、强度曲线胖度和形状参数变化时，可能影响整个岩石力学系统的稳定性状态，如图4至图5、图9至图12所示，但无论是稳定的断层无震滑动状态还是不稳定的地震失稳状态，当应力和总应变能重新进入增加状态后，约束反力的增速是相同的，断层上盘或下盘垂直位移的增速也是相同的.而当断层倾角不同时，如图6至图8所示，当应力和总应变能重新进入增加状态后，约束反力的增速以及断层两盘垂直位移的增速是不同的.这表明应力和应变能的增速由远场加载速度、岩石力学系统的结构和围岩材料属性决定，与断层软化特性参数无关.研究结果显示，断层浅部为高倾角70°时，深部为缓倾角35°时，岩石力学系统也会发生失稳，这从数值模拟角度支持了宫猛等(2020)得到的汶川地震破裂断层面倾角为35°的结果.

文中没有讨论重力的影响，这是因为本文重点关注的是断层软化特性对地震失稳的影响.定性来讲，考虑重力时会引起断层面上的正应力σn和剪应力τ发生变化，进而通过式(3)影响断层的破裂状态.但总体而言，重力并没有直接改变断层的软化本构特性，因为断层黏聚力式(4)和内摩擦系数式(5)并没有改变，因此重力对地震稳定性状态的影响是通过改变断层面上的应力间接实现的，并非导致地震失稳的本质原因，具体影响将在今后的工作中进一步讨论.

川西高原和四川盆地的材料参数的不确定性对地震稳定性状态的影响与重力的情况类似，都是通过改变断层面上的应力间接影响地震失稳，并不会改变整个岩石力学系统稳定和不稳定的2种状态，对于不稳定状态，仅仅会影响地震发生失稳的时间和地震失稳时的断层错距等.姚琪等(2012)分析了断层两盘岩性差异对汶川地震的影响.实际计算中，我们也对多组川西高原和四川盆地的材料参数模型进行了分析，进一步验证了以上结论.

汶川地震从孕育到发生的过程和失稳机制与图4和图5中的地震失稳情况是相同的，仅仅是平衡路径曲线的具体形态可能存在差异.基于前面的分析，总体而言，龙门山断裂带的高倾角铲形结构有助于孕育高达MS8.0的逆冲型地震.同时，龙门山断裂带的初始内摩擦系数μ0、初始黏聚力c0和强度曲线形状参数m可能都较大.尽管强度曲线胖度参数u0越大时更容易导致断层无震滑动，考虑到u0增加会导致断层闭锁时间增加，有利于积累更多的应变能，因此推测龙门山断裂带的u0值可能也较大.龙门山断裂带4个软化材料参数的综合效果是有利于整个岩石力学系统增加断层闭锁时间(地震孕育时间)，积累更多的应变能，以致于最终发生汶川MS8.0地震.

构成断层的介质均属于岩石类介质.大量三轴岩石力学实验结果显示，岩石在加载受力破坏过程中，当岩石的应力达到峰值屈服强度之后，随着变形继续增加，岩石强度会发生劣化或降低，称为岩石的软化特性.考虑到岩石介质的软化特性，马瑾和郭彦双(2014)开展了平直断层失稳的实验室模拟研究.实验加载时在X方向压力保持不变，Y方向按位移控制方式加载，且位移速率保持不变，最后得到差应力-时间的全过程曲线，完整体现了地震从孕育到突然失稳的全过程.本文平衡路径曲线的横坐标是远场位移加载总量，由于是匀速加载，因此横坐标与时间线性相关.纵坐标是四川盆地一侧右端面约束反力P，由于模型的上表面和底面均自由，因此约束反力P可视为垂向和水平向的差应力.因此把平衡路径曲线转换为垂向和水平向的差应力-时间曲线时，形态保持不变.本文数值模拟给出的地震失稳状态下的平衡路径曲线从形态上与马瑾和郭彦双(2014)的差应力-时间曲线完全一致，数值模拟结果与物理实验结果是吻合的.

最近，有学者采用基于区域多个震源机制解反演定量应力张量的方法对汶川地震前孕震区的应力状态进行了研究，推断孕震区在2007年中期达到应力峰值，并且获得了显著证据证明在峰值前应力随时间平稳变化并以积累为主，而在峰值后则转变为明显的应力释放阶段(王凯英等，2018).这表明汶川地震前，区域应力存在由积累为主转为释放为主的可观测阶段.该研究结果与地震失稳情况下在应力峰值点前后的应力变化特征是吻合的.本文为汶川地震前的应力变化研究结果从机理上给出了一种解释.

4 结论

本文考虑断层的软化特性，通过建立垂直于龙门山断裂带的汶川地震平面地震力学模型，从系统稳定性角度研究了汶川地震的孕育发生过程和失稳机制，探讨了断层倾角和断层材料参数变化对系统稳定状态和地震失稳过程的影响.研究表明，当断层倾角或断层材料参数变化时，系统可能表现为稳定的断层缓慢无震滑动或不稳定的地震失稳2种状态.初始内摩擦系数、断层倾角、初始黏聚力和强度曲线形状参数增大、或者强度曲线胖度参数减小均会导致整个岩石力学系统更趋向于不稳定的地震失稳状态.当发生地震失稳时，初始内摩擦系数越大、初始黏聚力越大，失稳时的应力降越大，相应地震震级更高.在相同的孕震条件下，断层倾角增加有助于地震的发生；倾角越小，储存的应变能可能通过断层无震滑动的方式释放掉，不容易发生地震.地震失稳前在应力峰值点和失稳点之间是断层加速错动的阶段，在该阶段应力开始减小，应变能开始释放，是失稳的前兆.无论是稳定的断层无震滑动状态还是不稳定的地震失稳状态，当应力和总应变能重新进入增加状态后，应力和断层两盘位移变化速率由远场加载速度、岩石力学系统的结构和围岩材料属性决定，与断层的软化特性参数无关.

致谢感谢三位匿名审稿专家为提高本文质量给出的有益意见和建议.