冲击波作用下引信传爆序列殉爆的数值模拟

肖向东，肖有才，蒋海燕，范晨阳，王志军

（1. 中北大学机电工程学院，山西 太原 030051；2. 西安近代化学研究所，陕西 西安 710065；3. 中国兵器工业集团公司西安机电信息技术研究所机电动态控制重点实验室，陕西 西安 710065）

引信传爆序列是爆轰能量传播的重要构件，序列中的含能材料通常具有较高的机械感度和冲击波感度，在外界作用下易发生爆炸或爆轰，导致殉爆现象发生[1-3]。

Kim 等[4-5]通过建立流体力学模型对PBXN-9 炸药开展了殉爆数值模拟研究，并将模拟结果与实验结果进行对比，得到了在一对多殉爆情况下，PBXN-9 炸药殉爆影响因素。Mostafa 等[6]利用一种轻型泡沫塑料对裸装炸药殉爆时的爆轰波历程进行了研究。陈朗等[7-8]计算了不同距离、不同工况下GHL 炸药的殉爆距离，得出了殉爆过程中爆轰波的成长规律，但所研究的爆轰波传播规律仅针对单个被发炸药，并没有涉及一对多以及被发炸药相互作用下爆轰波传播规律分析。

目前关于殉爆的研究很多，但主要针对裸装炸药或弹药殉爆，对不敏感引信传爆序列殉爆研究较少。本研究基于装填JH-14C 传爆药的某引信传爆序列结构，拟建立一种引信传爆序列殉爆特性数值模拟方法，结合见证板实验，验证模型参数，并利用冲击波超压得到冲击波能量方程。

1 有限元模型

1.1 材料模型

起爆药的未反应和反应产物均采用Jones-Wilkins-Lee（JWL）状态方程描述

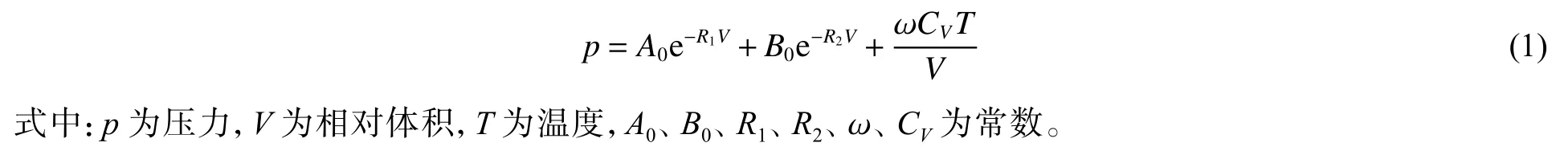
1.2 数值模型与方法

采用非线性有限元软件LS-DYNA3D，对冲击波作用下以JH-14C 为传爆药的引信传爆序列进行一对多殉爆数值模拟。起爆点设置于起爆药上端中心点处，考虑爆炸冲击波对引信传爆序列的冲击作用，引信传爆序列结构如图1 所示，其中T1～T8为选取的高斯点，传爆序列中JH-14C 的尺寸为 ∅38.0 mm × 15.5 mm。

图1 结构简图Fig. 1 Structure diagram

图2(a)为使用True Grid 软件建立的有限元模型，采用cm-g-μs 单位制建模，模型中主发引信传爆序列和周围空气介质采用欧拉法描述，网格尺寸2 mm；为便于观察爆炸和变形情况，被发引信传爆序列A1、A2、A3 和见证板采用拉格朗日法描述，网格尺寸1 mm，位置分布如图2(b)所示。

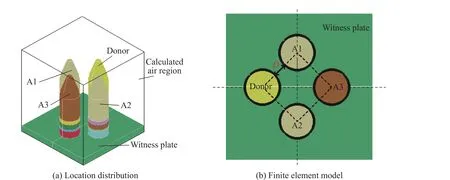
图2 位置分布与有限元计算模型Fig. 2 Location distribution and finite element model

1.3 材料参数

传爆序列殉爆数值模拟中，起爆药和传爆药分别为 Comp B、JH-14C，具体参数如表1[9-10]和表2[11]所示，其中：G为剪切模量， σy为屈服强度，p0为炸药的单位体积爆轰压力，D为爆轰波速，Figmax、FG1max、FG2min分别为炸药反应点火时、炸药反应增长时和炸药反应完成时的最大反应分数，I为点火常数，G1、G2分别为炸药反应增长和完成时的压力释放率。

表1 Comp B 炸药的High Explosive Burn 本构模型参数和JWL 状态方程参数[9-10]Table 1 High Explosive Burn constitutive model parameters and JWL equation parameters for Comp B[9-10]

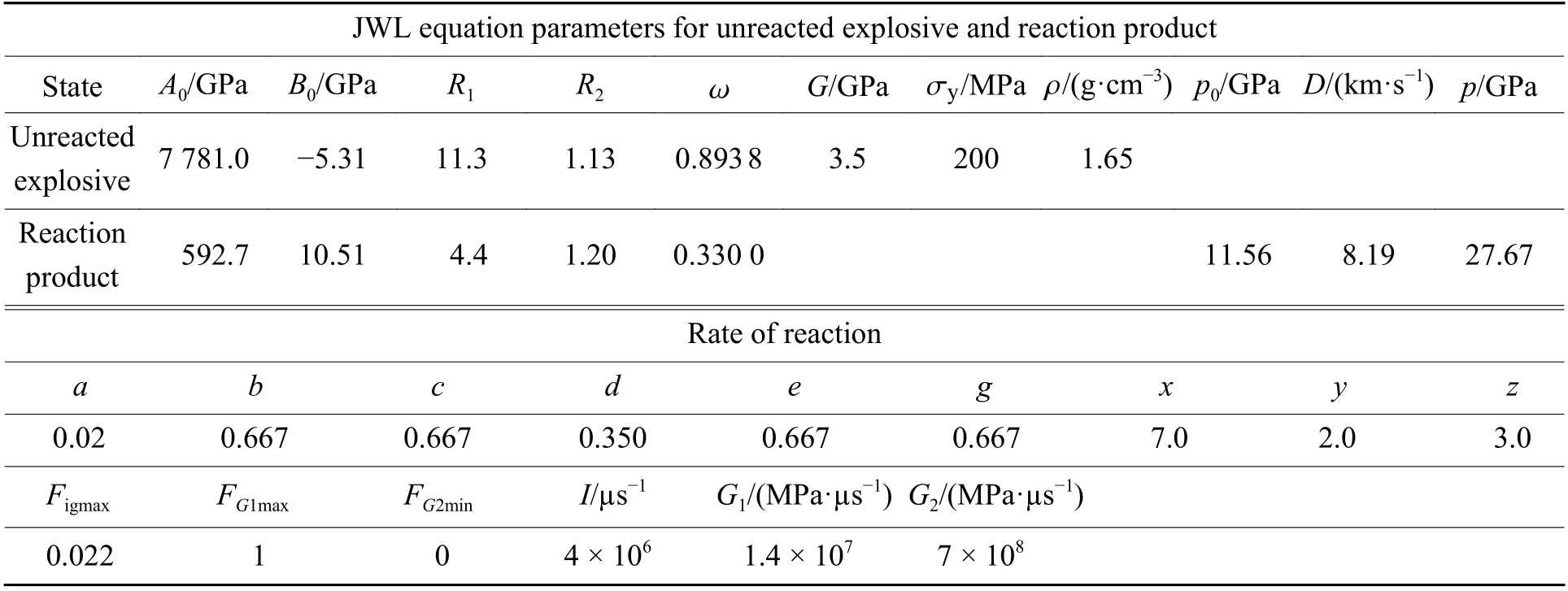
表2 JH-14C 的Lee-Tarve 参数[11]Table 2 Lee-Tarve parameters of JH-14C[11]

雷管座和隔爆板材料为2024 铝，保险机构为紫铜，见证板为4340 钢，3 种材料均利用Johnson-Cook本构方程和Grüneisen 状态方程，参数如表3[12-13]和表4[12-13]所示，其中：A、B、n、c、m为材料常数；Tm为材料熔化温度；Tr为参考温度，通常取为室温；Cp为比定压热容，具体参数均源于Autodyn 材料库。

表3 紫铜、2024 铝与4340 钢的Johnson-Cook 本构模型参数[12-13]Table 3 Johnson-Cook constitutive model parameters for copper, 2024 aluminum and 4340 steel[12-13]

表4 紫铜、2024 铝、4340 钢的Grüneisen 状态方程参数[12-13]Table 4 Grüneisen equation of state parameters of copper, 2024 aluminum and 4340 steel[12-13]

1.4 参数验证

为验证上述有限元模型以及参数的正确性，对单个引信传爆序列进行数值模拟，观察见证板的变形情况。有限元模型与实验装置如图3 所示。

图3 有限元模型与实验装置Fig. 3 Finite element model and experimental apparatus

4 次实验中见证板的变形情况如图4 所示。实验中采用雷管从引信传爆序列顶部引爆，见证板上凹坑深度分别为5.293、5.134、5.595、5.499 mm。图5 为数值模拟结果与实验数据的对比，其中数值模拟得到的凹坑深度为5.355 mm。由图5 可知，模拟结果与实验结果基本符合，凹坑深度的实验平均值与数值模拟结果的相对偏差约为0.47%，说明数值模型较好地描述了引信传爆序列爆轰行为。

图4 见证板变形Fig. 4 Witness plate deformation

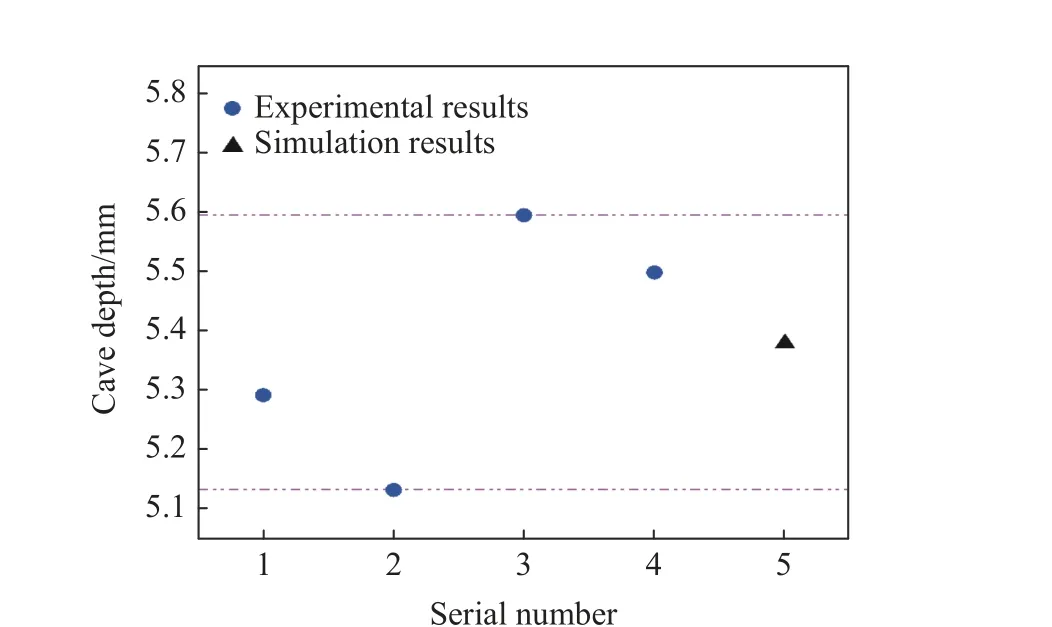
图5 凹坑深度Fig. 5 Cave depths curve

2 模拟结果与讨论

2.1 模拟结果

表5 为不同距离下殉爆数值模拟结果，表格中距离如图2（b）所示。结果显示：当距离小于9.7 mm 时，所有被发引信传爆序列完全爆轰；距离在9.7～10.3 mm 之间时，A1 和A2 传爆药部分反应，A3 未反应；距离大于10.3 mm 时，被发引信传爆序列均未发生爆轰。

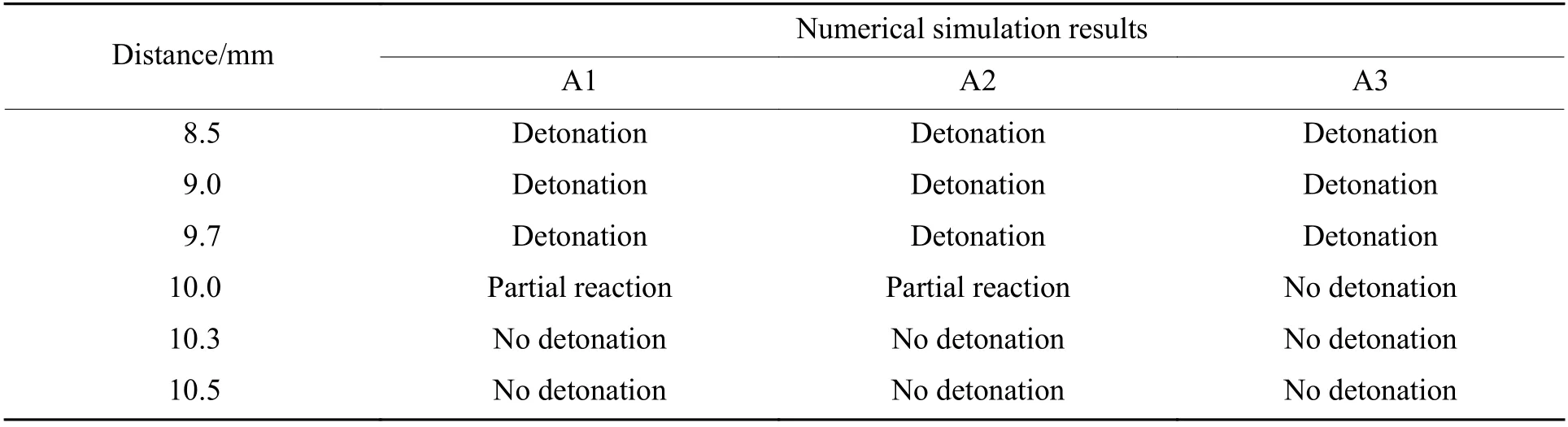
表5 不同距离下殉爆数值模拟结果Table 5 Numerical simulation results at different distances

图6 为距离9.0 mm 时被发引信传爆序列A1 殉爆压力云图。t= 10.0 μs 时，主发引信传爆序列爆轰波作用于A1 中的JH-14C，并从左上端开始向右下传播[14]。在此过程中，由于爆轰波的压缩作用，JH-14C 内部的空气隙或气泡形成局部热点。t= 21.0 μs 时，由于JH-14C 内部热点汇聚，压力上升，在右下端面发生爆炸，产生的爆轰波从右下端向左上端传播，在极短时间内引爆整个引信传爆序列。

在距离9.7 mm 时，不同时刻被发引信传爆序列A3 中传爆药变形和等压线如图7 所示。t= 12.0 μs时，主发冲击波作用于A3；t= 23.0 μs 时，由于A1 和A2 发生殉爆产生的冲击波作用于A3，因此从图6(c)中看出，A3 在侧面发生殉爆，形成爆轰波，并在极短时间内赶上主发冲击波；t= 26.0 μs 时，主发产生的冲击波与A3 产生的爆轰波在传爆药右部发生叠加继续往右传播。

图6 距离9.0 mm 时A1 殉爆压力云图Fig. 6 Pressure nephogram in the A1 at 9.0 mm

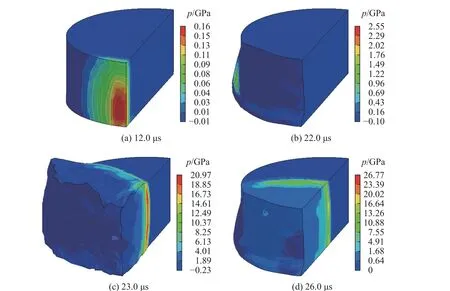
图7 距离9.7 mm 时不同时刻A3 中传爆药的变形和等压线Fig. 7 Deformation and isobaric lines of the explosive in the A3 at different times from 9.7 mm

2.2 结果分析

图8 为距离为9.7 mm 时，A1 和A3 的压力历程曲线。由图8(a)可知：t= 21.4 μs 时，A1 发生反应，高斯点T8处峰值压力约为6.4 GPa；随着反应进行，从t= 24.8 μs 开始，压力值逐渐升高，并发展成稳定爆轰波。由图8(b)可知：t= 12.0 μs 时，主发引信传爆序列爆炸产生的冲击波开始作用于A3，此时压力为0.8 GPa，不足以使引信传爆序列发生反应，但A1 和A2 在主发引信传爆序列爆轰波作用下发生殉爆，产生的爆轰波作用于A3；t= 24.0 μs 时，高斯点T1、T2、T3处压力发生明显的突跃，最高达到6.8 GPa，导致传爆药中热点增多，并产生局部高温区，A3 发生爆炸反应，并且逐渐发展为稳定爆轰。

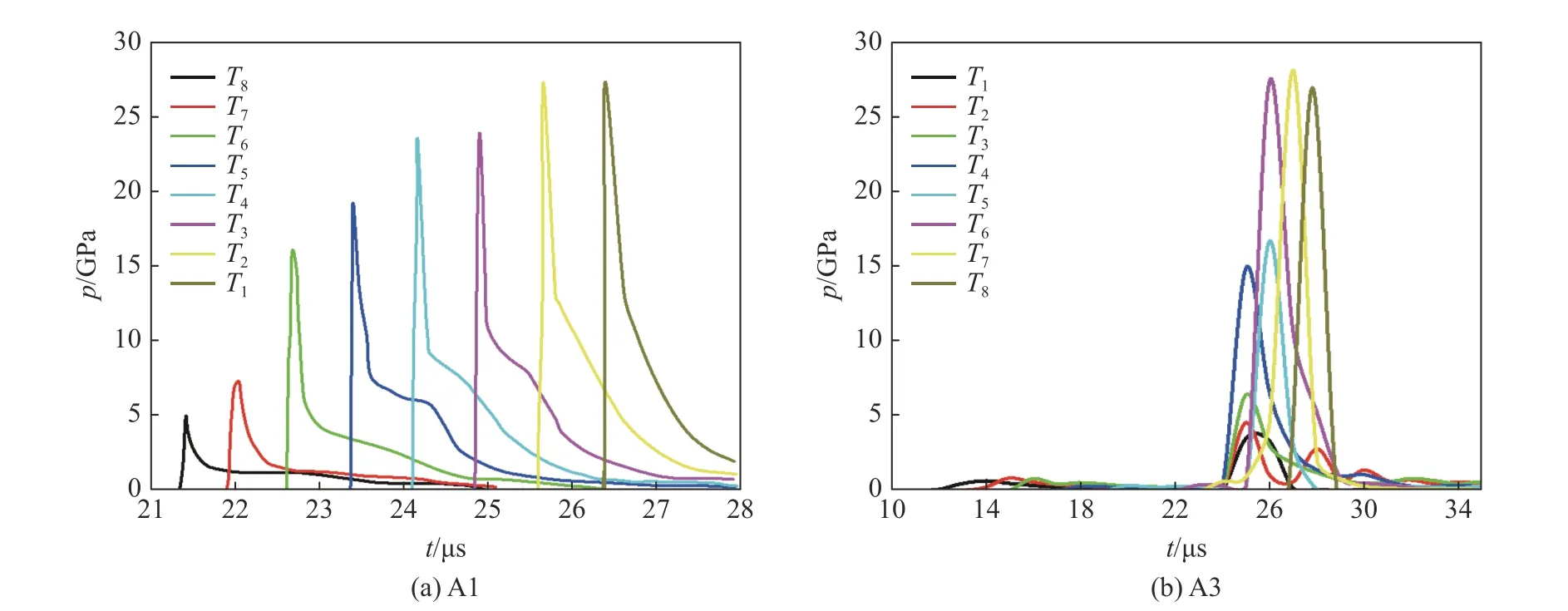
图8 距离为9.7 mm 时A1 和A3 中的压力曲线Fig. 8 Column of pressure curves in the A1 and A3 at 9.7 mm

图9(a)为距离10.0 mm 时A1 的压力历程曲线。由图9(a)可知，T8点峰值压力约为2.8 GPa，T7点峰值压力略有降低，T4点峰值压力接近8.5 GPa，而T3、T2、T1点压力呈下降趋势，说明部分炸药已发生反应，但没有形成稳定爆轰波。图9(b)为距离10.5 mm 时A1 的压力历程曲线。由图9(b)可知，t= 22.0 μs时，A1 中传爆药发生反应，T8点压力值为2.0 GPa，随着反应进行，压力值并无上升反而呈现衰减趋势。

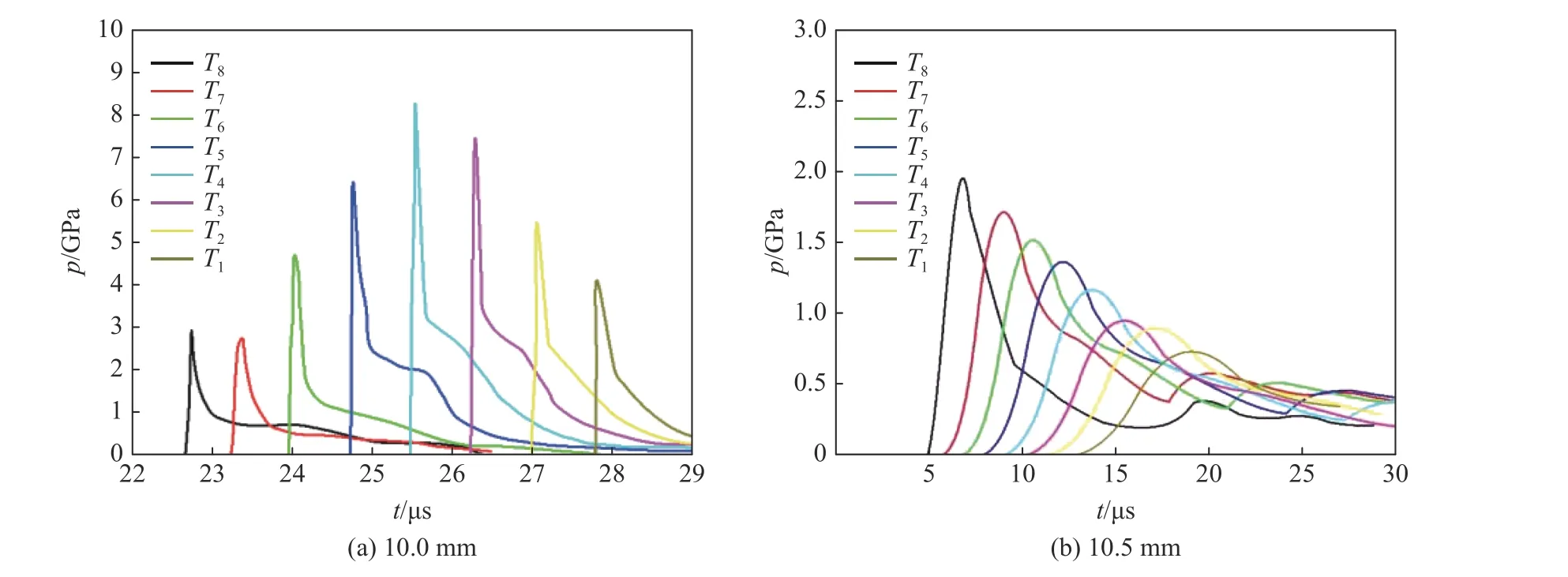
图9 A1 中的压力曲线Fig. 9 Column of pressure curves in the A1

2.3 冲击波能量判据

式中：Ec为起爆能量，tw为脉冲宽度，us为压力p时的冲击波速度。

由式(11)计算得到JH-14C 的临界起爆能量Ec= 4.93 × 105J/m2。

图10 为引信传爆序列中高斯点的能量曲线。由图10(a)可知，在距离9.7 mm 时，A1 中高斯点T4、T5处的能量高于临界起爆能量，发生殉爆。而在24.0 μs 之前，A3 中高斯点T4、T5处的能量低于临界起爆能量，但A1 与A2 产生的冲击波作用使压力发生突跃，内部能量也相应上升，并迅速超过临界起爆能量，致使A3 发生殉爆。由图10(b)可知，在距离为10.5 mm 时， A1 与A3 中的高斯点T4、T5处的能量低于临界起爆能量。

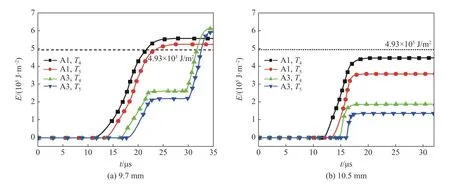
图10 引信传爆序列中高斯点能量Fig. 10 Gauss points energy of the fuze explosive train

3 结 论

（1）Comp B 为起爆药、JH-14C 为传爆药的引信传爆序列起爆实验中，见证板的凹坑平均深度约为5.38 mm，与模拟计算结果5.35 mm 基本吻合，由此验证了引信传爆序列模型参数的准确性。在此实际条件下，获得了引信传爆序列的临界殉爆距离为9.7 mm，殉爆安全距离为10.3 mm。

（2）以JH-14C 为传爆药的引信传爆序列殉爆过程中，冲击波由传爆药左端向右下传播，并在右下端面处起爆，之后爆轰波开始向左上传播，形成稳定爆轰波。

（3）建立了以JH-14C（ ∅38.0 mm × 15.5 mm）为传爆药的引信传爆序列冲击波能量判据，获得了JH-14C的临界起爆能量Ec为4.93 × 105J/m2。当作用冲击波能量大于Ec时，引信传爆序列发生殉爆反应。