含有小尺寸分层缺陷复合材料压力容器的应变响应及分析
2021-10-20柏慧,惠虎,杨斌,孔芳
柏 慧,惠 虎,杨 斌,孔 芳
(1. 华东理工大学机械与动力工程学院,上海 200237;2. 同济大学航空航天与力学学院,上海 200092;3. 枣庄科技职业学院,山东 枣庄 277599)
复合材料压力容器通常具有较高的比强度、比模量和较好的抗疲劳性能,能够实现整个系统的轻量化[1-3],被广泛应用于航空航天、民用储气和石油化工等领域。但是,这些复合材料压力容器会承受较大的力学载荷,如内压和冲击载荷,容器内部会产生目视不可检的损伤,使容器的承载能力大幅下降,从而对整个系统安全构成潜在威胁[4-6]。复合材料的损伤模式主要有基体开裂、脱粘、分层和纤维断裂。此外,应变也是常用于评价复合材料结构性能的一个重要参数。因此,研究含有不同损伤模式的复合材料压力容器的力学响应具有重要意义[7-10]。
近年来,对复合材料压力容器的设计优化、健康监测、损伤检测等已经开展了大量的研究。Zu 等[11-12]、Zhang 等[13]基于有限元模型,采用非测地线缠绕成型的方法,对含有不对称极孔、不同形状封头和开孔的复合材料压力容器进行了应力分布和极限强度模拟分析,进而设计和优化了符合工况要求的压力容器。Hao 等[14]将光纤布拉格光栅传感器安装在筒体环向和轴向,研究了玻璃纤维增强塑料压力容器中损伤的增长,结果表明,电测法可用于监测复合材料压力容器的应变变化。Liu 等[15]基于连续损伤力学,采用显式有限元方法开展了渐进失效分析,用3 种不同几何尺寸的复合材料压力容器预测了铝碳纤维/环氧复合圆柱层合板结构的失效性能和爆破强度,并且通过实验和隐式有限元分析,比较了采用显式有限元分析的复合材料层合板的预测失效强度。王莉等[16]通过建立复合材料板分层损伤参数与超声波法检测损伤指数的定量关系,提出了一种基于代理模型的分层损伤定位检测法,通过损伤指数的计算,可得到对应的分层损伤面积。Khechai 等[17]采用实验和有限元模拟方法研究了含有不同尺寸圆孔的复合材料板在拉伸力载荷下应力的分布情况,并与数字图像扫描结果进行了对比,发现数值模拟结果与实验结果一致。在上述工作中,研究人员均考虑了复合材料压力容器的缺陷,但是很少考虑内部缺陷,因而无法判断整个压力容器的健康情况,因此,需要对含有内部缺陷压力容器的力学行为进行分析,为容器的安全监测和检测提供一定的数据基础。
本研究对玻璃纤维缠绕环氧树脂基压力容器进行水压试验和电测法测取应变,并采用有限元软件Abaqus,通过调用用户子程序中的材料参数、失效判定准则和刚度递减参数,对压力容器加载内压力,并与试验结果对比分析,此外,利用该模型对含有不同程度分层的压力容器进行应力分析,同时对比数值模拟结果,分析不同缺陷对复合材料压力容器应变的影响。
1 水压试验和数值模拟
1.1 材料和制造过程
复合材料压力容器的制造过程如图1 所示。在圆柱形模具上涂上脱模剂后缠绕带有环氧树脂预浸料的玻璃纤维,缠绕角度为78°,接近于环向,到一定厚度脱模,与加工好的封头连接,再用纤维布加强连接处,最后在容器外壁刷一层透明胶衣。该容器内径为1 600 mm,高1 620 mm,厚18 mm,水容积为3 m3,设计压力为0.375 MPa。在压力容器筒体段取下试样,根据ASTM D3039/D3039M-08标准,在0°、90°和45°方向上的试样尺寸分别为220 mm × 25 mm × 18 mm、220 mm × 25 mm × 18 mm 和160 mm × 25 mm × 18 mm,0°试样与环向平行,90°试样与纵向平行,每种试样各5 个,均在INSTRON-8801 试验机上测试,位移速度为2 mm/min,测试结果分别如表1[18-19]和表2[18-19]所示,其中:E1、E2和E3分别表示纤维方向、垂直纤维方向和试样厚度方向的拉伸模量,G12、G13和G23表示3 个面内的剪切模量,v12、v13和v23表示3 个面内的泊松比,XT和XC分别表示纤维方向的拉伸和压缩强度,YT和YC分别为垂直纤维方向的拉伸和压缩强度,ZT和ZC分别为试样厚度方向的拉伸和压缩强度,S12、S13和S23表示3 个面内的剪切强度。
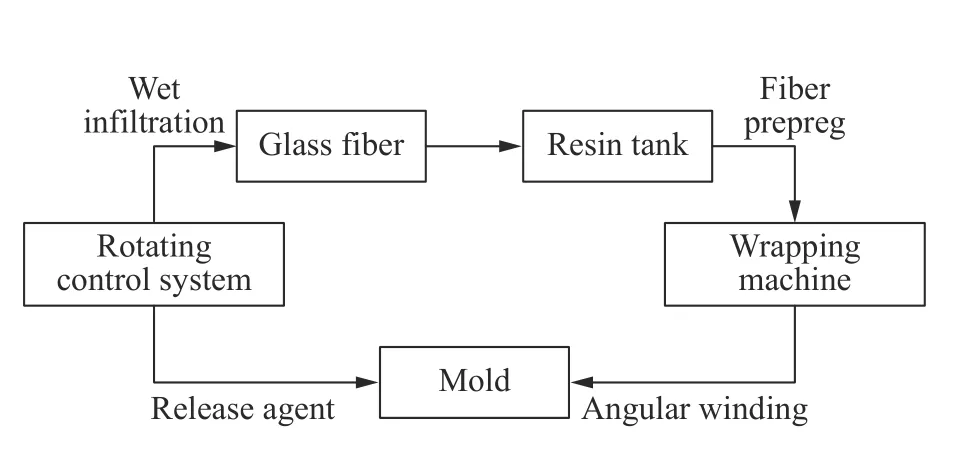
图1 纤维缠绕压力容器的制造示意图Fig. 1 Schematic diagram of fabrication of the fiber wound pressure vessel

表1 玻璃纤维/环氧树脂复合材料板的刚度参数[18-19]Table 1 Stiffness parameters of glass fiber/epoxy resin composite plate[18-19]

表2 玻璃纤维/环氧树脂复合材料板的强度参数[18-19]Table 2 Strength parameters of glass fiber/epoxy rsesin composite plate[18-19] MPa
1.2 水压试验和应变测量
电测法是将作为传感元件的电阻应变片粘贴或安装在被测的压力容器表面,然后将其接入测量电路,当设备受载变形时,应变片的敏感栅相应地变形并将应变转换成电阻改变量,再通过电阻应变仪直接得到所测量的应变值。水压试验和应变测量系统如图2 所示,打压设备连接水管向压力容器中注水,加压速率为0.05 MPa/min,最大加载压力是设计压力的1.25 倍,当压力达到0.100、0.200 和0.375 MPa时,压力维持4 min,在加压过程中,同时测量压力容器筒体的应变变化情况。共设置5 个测量点,均匀分布在筒体一周,每个测量点有两个平行测量点并粘贴两组应变片,一组应变片包括周向和纵向两个方向,测量筒体外壁的应变,两个测量周之间的轴向距离为100 mm。应变片型号为BX 120-3BA;光栅和基底尺寸分别为3 mm × 2 mm 和10.3 mm × 10.3 mm;应变仪型号为XL2101GE60,应变仪主机自带60 测点扫描箱,并配置USB 2.0 和网络接口,一台计算机最多可同时控制10 台同类型仪器,即组成多点测量系统。同时,该系列仪器采用精度高、稳定性强的运算放大器和数字滤波技术,因而具有非常高的测量精度、良好的稳定性和极强的抗干扰能力,对工程应变、载荷测量都具有广泛的适用性。

图2 水压试验和应变测量系统Fig. 2 Hydraulic test and strain measurement system
1.3 数值模拟方法
利用Abaqus 软件建立了用于预测复合材料压力容器在内压载荷作用下应变响应的三维有限元模型。同时,根据复合材料层合板的结构特点,编写了用于判断材料失效的VUMAT 用户子程序。在Abaqus/Explicit 软件中建立了三维有限元模型,对玻璃缠绕压力容器的应变演化进行了分析。根据复合材料层合板的结构特点,在VUMAT 用户子程序中采用Hashin 失效准则求解压力容器在内压作用下的准静态问题。而扩展的Hashin 3D 失效准则考虑到了厚度方向的应力,将原来的二维准则扩展到了三维,并增加到了6 种破坏模式,分别为纤维拉伸失效、纤维压缩失效、基体拉伸失效、基体压缩失效、拉伸引起的分层和剪切引起的分层:
纤维拉伸断裂
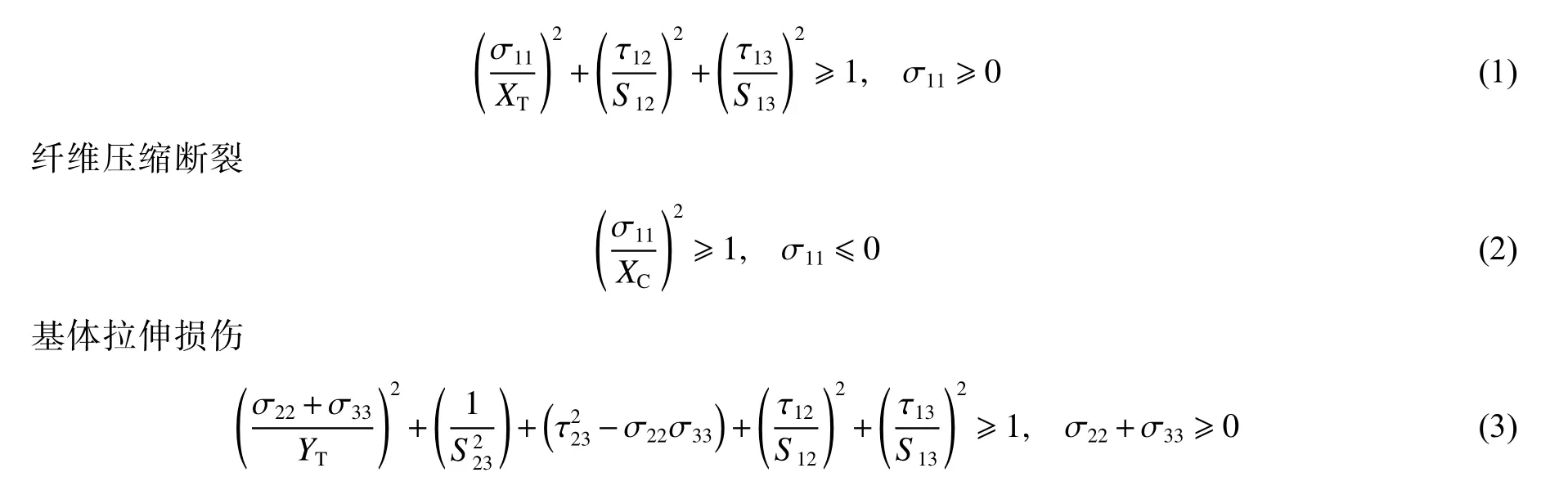
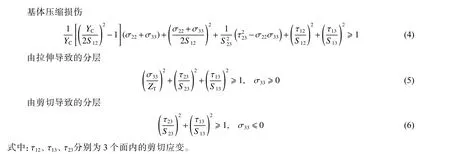
如果任何一个失效判定准则达到1,则判定为该点发生损伤,对相应的材料刚度进行折减。不同的载荷水平或载荷形式将产生不同的破坏模式,一旦有某个单元满足Hashin 3D 准则的某一个或多个判定条件,则认为材料积分点发生损伤,对相应的材料属性进行折减,折减方法为对材料的弹性模量直接乘以折减系数,并利用折减后的属性重新计算局部材料刚度。基于该结论,VUMAT 中选定的刚度降级参数列于表3 中。

表3 玻璃纤维压力容器的材料刚度递减规则Table 3 Decreasing rules of material stiffness for glass fiber pressure vessels
1.4 试验及模拟结果讨论
该压力容器的厚度为18 mm,均分为6 层复合材料圆柱壳,每层3 mm,有限元模型分别包含34 290 个单元和70 434 个节点,有限元模型如图3(a)所示,底面施加固定约束,内压加载到内表面,模型考虑了大变形的非线性效应,计算采用牛顿-拉夫森迭代算法,结果如图3(b)所示。
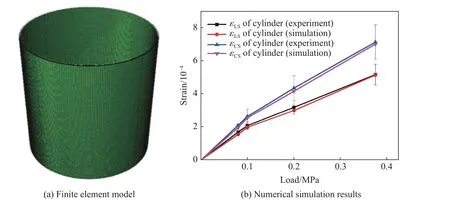
图3 有限元模型与数值模拟结果Fig. 3 Finite element model and numerical simulation results
由图3 可以看出,随着内压增加,应变逐渐增大。当内压分别为0.100、0.200 和0.375 MPa 时,筒体的周向应变 εCS分 别为2.102 × 10-4、4.359 × 10-4和7.141 × 10-4,纵向应变 εLS分别为2.079 × 10-4、3.197 × 10-4和5.175 × 10-4。结果表明,该筒体的周向应变分别为纵向应变的1.01、1.38 和1.37 倍。内压分别由0.100 MPa 增加到0.200 MPa 和由0.200 MPa 增加到0.375 MPa 时,筒体的周向应变增加率分别为197.23%和63.80%,而纵向应变的增加率分别为53.73%和61.89%。可以看到有限元模拟与水压试验测量的应变结果误差小于12%。
2 小尺寸缺陷对应变的影响
损伤的定性和定量分析一直是复合材料压力容器损伤检测的难点,利用上述方法,通过建立含有不同损伤程度的复合材料压力容器的有限元模型,在外加不同载荷的情况下,得到不同损伤程度下应变的分布和损伤指数(应变与分层或断裂损伤参数间的定量关系),从而为损伤定位与定量检测提供一定的参考。
2.1 有限元模型
带有分层损伤的复合材料压力容器在受内压载荷作用下,压力容器各处的应变变化不明显,也就是说,用内压加载的方式很难得到应变数值与分层损伤面积的函数关系。通过查阅相关文献得知,在冲击载荷作用下能够很好地得出两者之间的关系和应变分布,因此,对于分层损伤的有限元模拟,载荷采用冲击载荷。根据ASME X 的附录6,最大损伤长度不超过150 mm,因此设置小尺寸分层损伤的直径(D)为10、20、30、40 和50 mm,分层位置及边界条件如图4 所示。分层位于筒体中间,第3 层和第4 层层合壳之间,分层形状为圆形,最外层筒体被分割以便于网格划分,在筒体两端施加固支载荷,在分层损伤的中心处施加位移载荷,3 个载荷步分别为0.3、0.6 和0.9 mm,共包含87 202个节点和42 867 个单元。
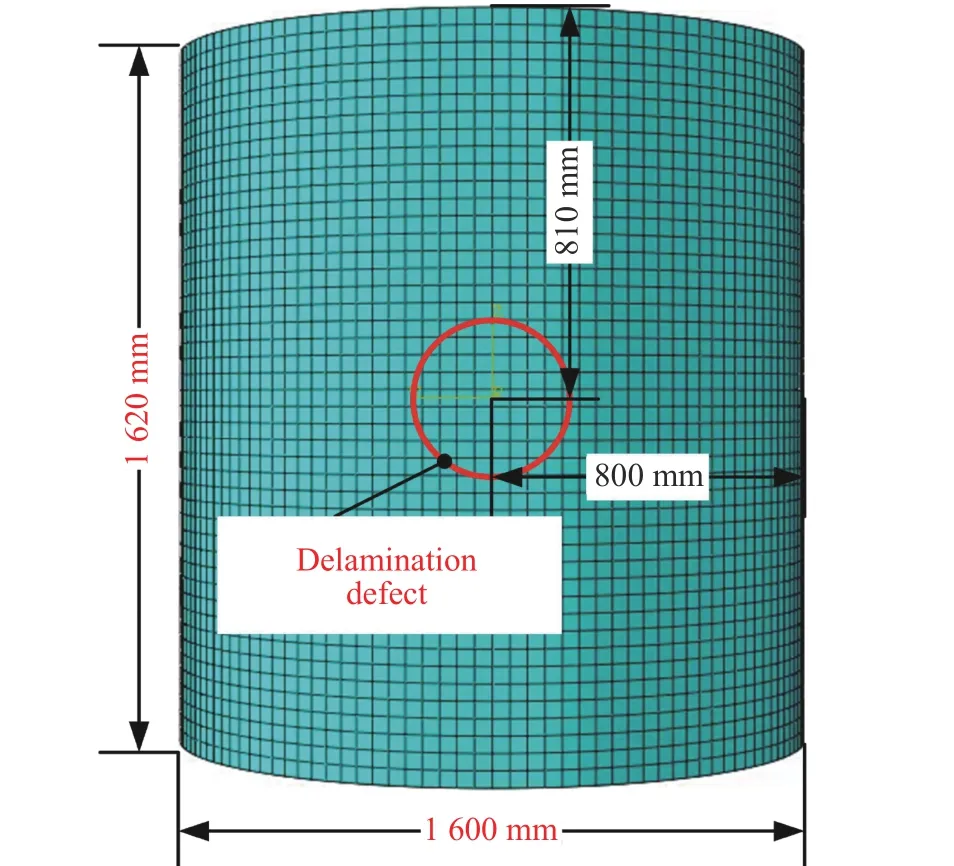
图4 含有分层缺陷压力容器的有限元模型Fig. 4 Finite element model of a pressure vessel with stratified defects
2.2 有限元模拟结果及定量分析
无分层损伤和有分层损伤时含有不同尺寸分层缺陷复合材料压力容器的应力分布结果如图5 所示。总体来看,随着载荷位移S的增加,最大应力也不断增加,且最大应力位于加载位置处,沿着分层圆径向逐渐变小,等应力线呈菱形,周向应力递减阶梯大于径向。由图5(a)可知,当无分层损伤,载荷位移分别为0.3、0.6、0.9 mm 时,最大应力分别为1.884、5.655 和11.300 MPa;由图5(b)可知,当分层直径为10 mm,载荷位移分别为0.3、0.6、0.9 mm 时,最大应力分别为2.530、7.564 和15.080 MPa;由图5(c)可知,当分层直径为20 mm,载荷位移分别为0.3、0.6、0.9 mm 时,最大应力分别为2.531、7.565 和15.080 MPa;由图5(d)可知,当分层直径为30 mm,载荷位移分别为0.3、0.6、0.9 mm 时,最大应力分别为2.528、7.556 和15.060 MPa;由图5(e)可知,当分层直径为40 mm,载荷位移分别为0.3、0.6、0.9 mm时,最大应力分别为2.532、7.564 和15.080 MPa;由图5(f)可知,当分层直径为50 mm,载荷位移分别为0.3、0.6、0.9 mm 时,最大应力分别为1.893、5.666 和11.310 MPa。可以看到,分层面积对复合材料最大Mises 应力的影响较小,因此进一步研究应变的分布。
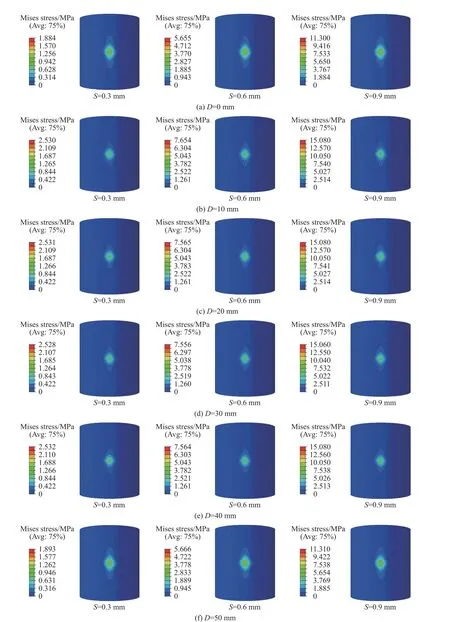
图5 含有不同尺寸分层缺陷复合材料压力容器的应力云图Fig. 5 Stress contour of composite pressure vessel with different delamination defects
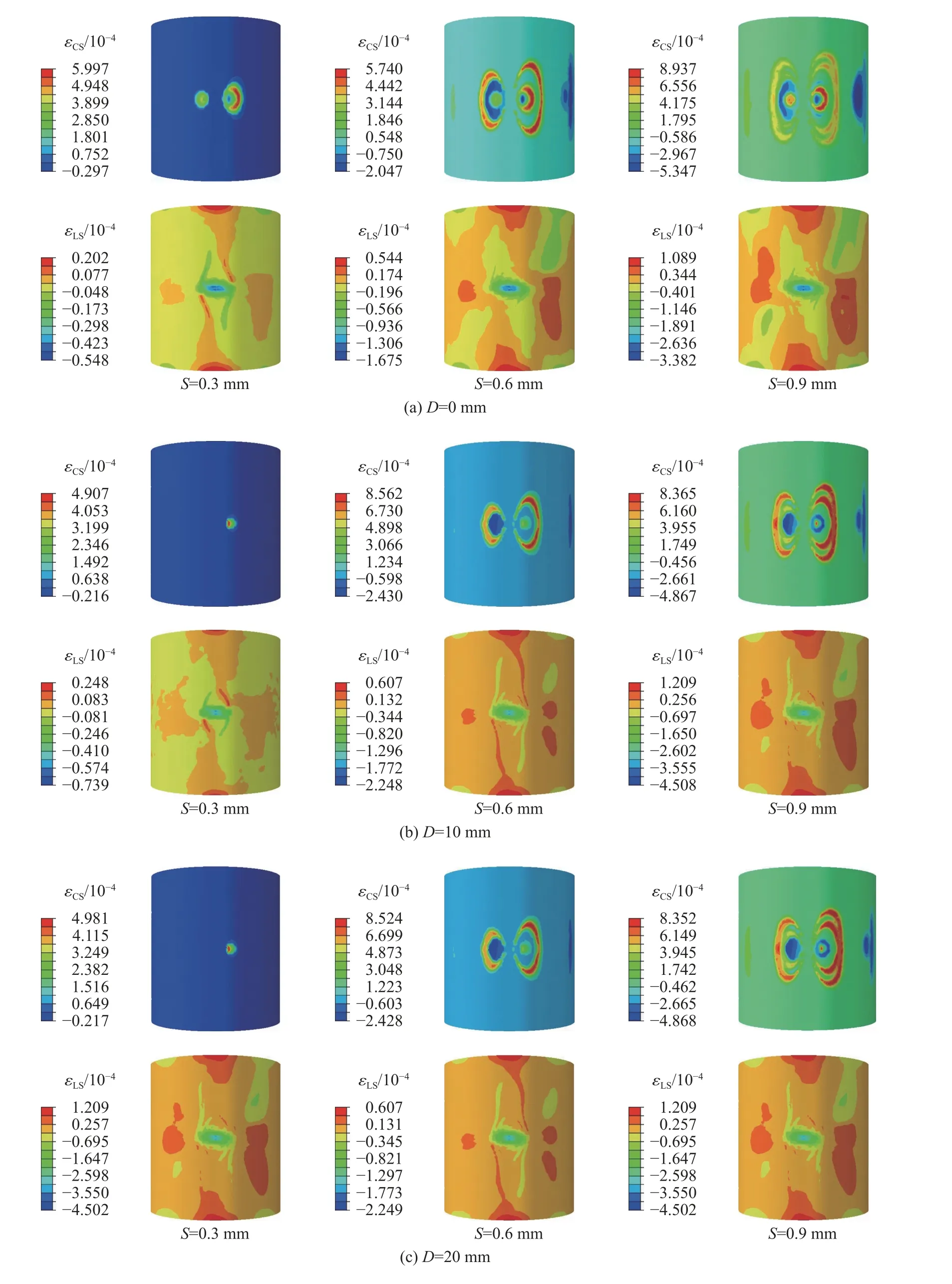
含有不同尺寸分层缺陷复合材料压力容器的应变云图如图6 所示。图6(a)为无缺陷复合材料压力容器在受到位移载荷作用下周向应变和纵向应变的分布云图,图6(b)~图6(f)为分层损伤D分别为10、20、30、40 和50 mm 复合材料压力容器在受到位移载荷作用下周向应变和轴向应变的分布云图。

图6 含有不同尺寸分层缺陷复合材料压力容器的应变云图Fig. 6 Strain contour of composite pressure vessel with different delamination defects


2.3 分层缺陷的定位分析
由上述分析可知,复合材料压力容器在受到外部位移载荷时,其周向应变 εCS大 于纵向应变 εLS,εCS和 εLS的 分布具有明显的特征,即 εCS呈 椭圆形分布,而 εLS在位移加载处产生最大压应变,共同之处是应变都随着位移载荷的增加而增大。
为了更系统地研究复合材料压力容器上的应变分布以及应变与损伤位置和程度的关系,图7所示为沿着复合材料半周路径上应变随距离的变化分析路径的选择。从图7 可以看出,路径在压力容器的最外层,分层损伤位于路径中间位置。
图7 分析路径的选择Fig. 7 Selection of analysis paths
图8 则是在不同位移加载作用下应变沿路径上距离的变化曲线。可以看到,随着位移载荷的增加, εCS变 化曲线愈加复杂,而 εLS始 终是先减小后增大的趋势,在位移载荷中心处, εLS为最大压应变。通过以上分析可知:当位移载荷为0.9 mm 时,应变变化规律更明显, εCS和 εLS与分层损伤程度及位置无明显函数关系,且此方法与加载位置密切相关。
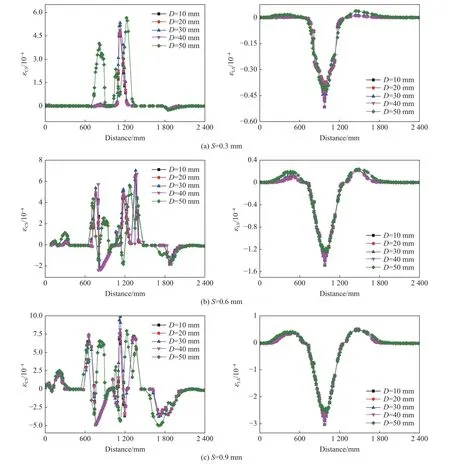
图8 不同分层面积应变沿路径的变化曲线Fig. 8 Variation curves of area strain in different layers along the path
3 总 结
采用玻璃纤维预浸料环氧树脂缠绕成复合材料压力容器,对其进行水压试验和原位应变测量,并与有限元模拟结果对比分析,来探究小尺寸分层缺陷与应变的关系,得出以下主要结论:
(1)电测法可以用来测量复合材料压力容器的应变,原位应变会随着水压的增加而增大,能即时显示复合材料的力学变化;
(2)使用VUMAT 用户子程序的渐进损伤有限元模型可以较准确地预测复合材料的应变变化,与试验结果的误差小于12%;
(3)含有小尺寸分层缺陷的压力容器在位移载荷作用下周向应变为主要应变,最大纵向应变和Mises应力位置与加载位置重合,且最大Mises 应力随分层面积的增加而增大。