工程扰动下矿山高陡边坡力学响应规律研究
2021-10-20贾新昆卢邦飞
贾新昆 卢邦飞
(天津华北地质勘查局,天津300170)
随着现代露天采矿工艺技术与安全科学的发展,越来越多的矿床能够满足新环境下的露天开采条件。然而,随之产生了大量的高陡边坡与凹陷露天深坑,受区域环境影响,加上开采过程中各种生产扰动,使得边坡构造发生变化,在开采工作区周围出现一系列力学现象或岩层内部损伤,进而可能导致崩塌、滑坡、地面塌陷、泥石流及不稳定斜坡等地质灾害[1]。如何在保证矿石开采的同时,兼顾边坡与露天坑整体稳定性,有效防止自然与人为因素对边坡稳定性的破坏,是露天采场安全高效生产的重中之重。近年来,我国金属非金属矿山露天开采深度增长明显,一方面由于露天开采本身存在诸多安全高效的优点,另一方面我国露天开采技术也在逐步成熟与进步,机械化和深孔穿凿爆破工艺技术等方面均有长足的发展[2]。同时,随着土地复垦与露天矿二次开发的广泛推行,我国矿业未来将以实现“绿色采矿,无废开采”[3]为目标。然而,随着露天采矿逐步向深部发展,高陡边坡与深凹露天坑的增加,造成了大量的安全隐患。我国安全环保管控力度正逐步加大,工程扰动下的露天矿边坡稳定性研究也逐步成为重要的科研课题[4]。
从国内现有成果来看,对边坡稳定性研究所采用的方法主要有弹性理论、承压理论,现行的相关理论也重点围绕这些方法来展开应用研究。安全系数是边坡稳定性分析与评价的关键指标,其来源主要是依据边坡体的强度与本构特性。相似模型模拟、有限元、离散元、边界元等数值分析模拟方法理论以及现场实测分析等方法,是当前边坡稳定性分析的常用方法。其中,刘畅[5]提出了“转动滑坡”、“结构面控制”、“空洞的影响”及“差异沉降”这4种构想;刘殿柱[6]利用Matlab软件对有代表性的数据进行频域分析及回归分析处理,总结了高陡边坡的爆破振动特点及爆破振动衰减规律;董英健等[7]以露天矿开采为例,对露天边坡爆破开采的危险源进行了分析,并提出了露天矿山爆破安全的预防和治理措施;严鹏等[8]通过回归分析建立了不同爆心距处质点峰值振动速度与损伤深度的关系;胡英国等[9]针对预裂爆破等两种不同方式,应用LS-DYNA软件平台进行二次开发,成功模拟仿真出损伤时变效果,得出岩石高陡边坡在2种开挖方式下最终保留岩体的损伤分布特征;杨天鸿等[10]基于国内外边坡稳定性研究成果,结合“边坡岩体渐进损伤破坏是边坡岩体失稳前兆本质特征”这一思路,提出了露天矿边坡岩体强度参数识别表征方法和动态稳定性评价方法。然而,随着开采深度逐年增加,传统分析方法难以解决高陡边坡的复杂问题,针对应力、位移和塑性区的稳定性分析方法比较简单,且大多侧重考虑单方面因素对边坡稳定性的影响,缺乏多方面的分析,因而存在一定的不合理性。
针对某露天矿山高陡边坡复杂多因素影响导致滑坡、泥石流以及大范围崩塌的工程实际[11],在研究高陡边坡稳定性分析相关理论的基础上,结合相关边坡优化理论,综合考虑区域地质条件,建立边坡稳定性分析的三维数值模型,并从应力迁移与动力扰动相结合的角度进行分析,以安全生产与环境保护为目标,开展露天矿山高陡边坡稳定性优化研究。
1 高陡边坡工程技术条件
露天采场平面呈椭圆形,长轴宽度与短轴宽度分别为646 m和601 m。岩性以似斑状二长花岗岩为主,剥离后露天采场边坡角为55°,随着开采的推进,在区域内形成了高陡边坡。本研究所选计算区域为矿区1号采坑,根据境界圈定原则和边坡参数,确定+315 m以上为山坡露天开采,+315 m以下为凹陷露天开采。露天采场规划布置采用螺旋形坑线,布置在各采坑边帮上,形成环形固定坑线,如图1所示。原采坑按顺时针方向下降展线,至坑底+60 m标高平台。1号采坑按逆时针方向下降展线,至坑底+35 m标高平台。采坑预计最终深度将到达300 m,为矿山最突出的高陡边坡露天采坑,因此针对这一区域展开研究具有代表性。通过圈定露天境界,获得开采境界尺寸数据为台阶高度15 m,坡面角65°,边坡角43°~47°。1号采坑边坡角为45°~46°
数值模型以1号采坑境界圈定为依据,其尺寸为:上部长1 167 m,宽894 m,底部长338 m,宽254 m,顶部标高+375 m,当前底部标高+190 m。采坑内部使用穿孔作业,每日3班,干孔采用乳化粉状炸药,水孔采用浆装乳化炸药,钻孔采用“Ⅴ”形布置,采用非电导爆管排间微差起爆的松动爆破方式。矿山一次爆破作业量见表1。

爆破动力数值模拟选取的深凹高陡边坡研究区域如图1所示,其边坡轮廓线与渗流分析模型一致,均为高陡边坡。

2 显式—隐式分析模型联合构建
2.1 显式—隐式算法转换
显—隐结合的计算模型需要借助ANSYS与LSDYNA仿真软件平台。ANSYS软件静力学隐式分析的主要原理是通过迭代法解方程组,这种方程组是非线性的,对变形比较小的问题求解效果较好;但对于大变形的求解精度将会降低很多,且收敛性一般。其求解方法的优点在于,时间步长可调范围大,计算精度与整体计算过程并行,迭代次数越多,精度也越高。一般来说,数值模拟的计算时间成本大多与自由度数目紧密相关。LS-DYNA软件以显式分析见长,属于非线性计算软件,但还具有隐式分析功能。显式分析的特点是需要考虑时间,即计算过程中需要对时间进行差分,因此不存在多次迭代后不收敛的问题,其最小时间步长受最小单元尺寸控制。
为了在高陡边坡动力稳定性分析中考虑地应力的影响,如果在LS-DYNA软件中施加载荷则该变量具备时变性,因此计算过程中荷载会随时间一直持续下去,与现实情况不符。故通过ANSYS软件计算地应力时,待地应力收敛后,将地应力数据文件导入LS-DYNA软件中进行爆破动力计算[12-13]。显式—隐式分析的主要步骤如图2所示。
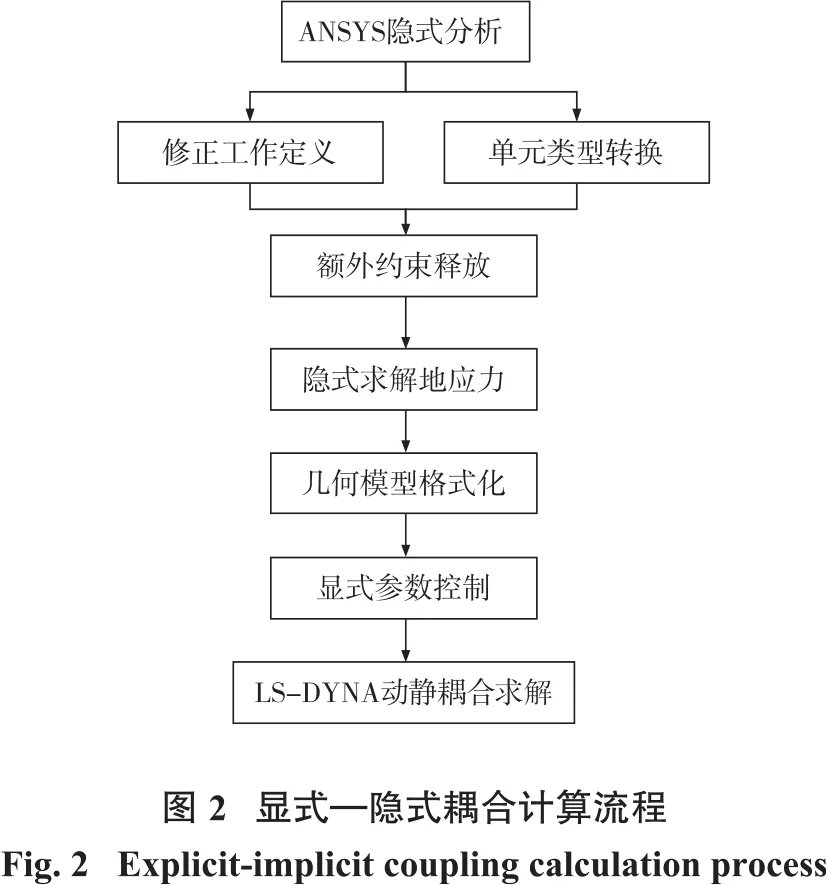
首先根据矿山实测边坡剖面建立边坡坡体数值模型,划分网格并赋予材料参数,求解获得地应力分布结果;然后清理边坡体上部覆盖的岩土体,即进行开挖,获得土体剥离后的高陡边坡应力分布结果。静力学计算结束之后更改工作名,再保存文件。如果没有此项操作,在完成显式求解后,隐式结果文件会被覆盖。隐式分析与显式分析单元类型有所不同,隐式分析时采用的是3D solidf185单元,在进行爆破动力分析时一般采用3D solid164显式单元。工作名更改完成后选取“隐式—显式转换”模式并确认,即完成单元类型转换。在隐式求解设置过程中,边界条件设置与显式边界条件有很大区别。故转换到显式设置界面后需将多余的边界条件去除,再添加显式动力求解所需的边界条件。此步骤是显隐转换的关键,显式设置界面通过读取该文件进行显隐计算关联。
Drelax文件中的位移和转动被赋值于显式分析结构中,并且考虑了计算前期收敛的地应力预荷载。“Dynamic relax”命令指示LS-DYNA软件求解器使用动力松弛进行应力初始化。静态分析在虚拟时程上进行,在时间步内,所有动能由阻尼消除。在进行显式分析时,需要定义时间相关变量,设置完后生成K文件,修改岩石及炸药材料参数保存为最终K文件。调用LS-DYNA Solver,递交K文件进行求解。
2.2 材料参数及模型构建
将边坡模型导入ANSYS软件中,显式动力学计算时由于施加了爆破载荷,在模型相应边界需施加无反射边界条件来模拟无限大区域,消除应力波反射作用对分析结果的影响。对于无反射边界条件的施加,三维单元较二维单元更为方便快捷,仅需选择边界节点建立节点组,通过命令施加即可。考虑到二维与三维模型各自优点,建立了准二维数值模型,即在Z方向仅取一个单位长度20 cm,并且在Z方向施加位移约束,有利于选取边界节点建立节点组施加无反射边界条件。
材料模型采用MAT_PLASTIC_KINEMATIC材料模型[14-15],该模型考虑了弹塑性力学特征。在应力未到达屈服应力前,应力与应变之间通过杨氏模量系数E进行关联,应力超过屈服点后,应力—应变关系通过小于杨氏模量的切线模量系数Et进行关联,其本构模型如图3所示,图中l0与l表示试件单轴压缩时的未变形及变形后的长度。
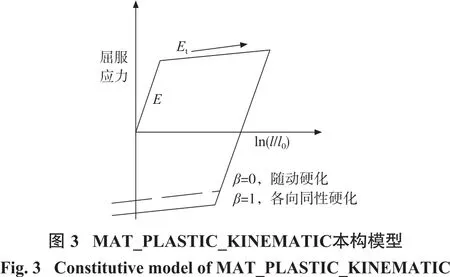
图3中所示硬化参数β在[0 ,1]区间内取值,对应的材料特性为:随动硬化模型β=0,混合硬化模型0<β<1,各向同性硬化模型β=1。等向强化模型假定材料在塑性变形后,仍保持各向同性性质,忽略了由于塑性变形引起的各向异性的影响,模拟中将岩石视为随动硬化模型(β=0)。岩石材料本构模型为

式中,σ为应力,GPa;ε为应变;E为弹性模量,GPa;σy为屈服应力,GPa;H为应变硬化指数,Et为切线模量。
岩石物理力学参数取值见表2。

模型一般采用高爆材料模型与JWL状态方程来定义[16-17]。ANSYS软件中并无该材料模型,需采用其它材料定义,在K文件中手动添加相关关键字来赋值材料参数。LEE于1965年在JONES和WILKINS工作的基础上提出了JWL方程[18]:

式中,P为爆轰压力,MPa,V为相对体积;Ev为单位体积内能,J/m3;ω,A,B,R1,R2为材料参数。岩石炸药材料参数取值见表3。

注:LS-DYNA单位制采用cm-g-μs。
在边界条件方面,显式与隐式分析的边界条件有所不同。模型静力分析的边界条件采用定向位移约束,坡面边界忽略地表起伏,设定为自由面。转换为动力分析界面后,边坡上覆岩体已经剥离,左右边界及下边界增加溢出边界条件,药包模型布置在边坡最低台阶位置。
3 模型运算及工程应用
3.1 动静耦合力学分析
3.1.1 静力状态
在开挖前,初始应力采用自重应力加载和单元清除的方式生成,水平应力均匀设置,且应力值随深度增加而增加。初始应力计算过程中采用线弹性材料,故无塑性区形成[19]。模型选取的高陡边坡区域长210 m,高180 m,清除单元总数为13 329个。初始应力计算结果如图4和图5所示。
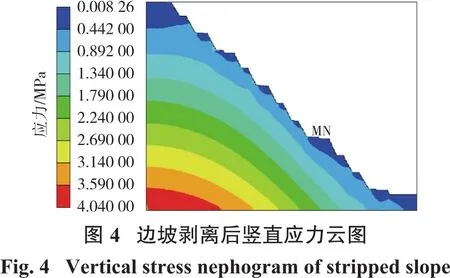

边坡上部单元剥离后产生卸荷力学作用,由于上层岩体约束被解除,边坡面形成了部分回弹效应,坡面应力值骤减。模型下边界应力值逐级减小,也是由于失去上覆压力造成的。高应力区主要集中在边坡体原点位置,低应力区主要分布在坡面。当受到剧烈爆破振动影响时,坡面会率先发生动力响应,且极易发生破坏。因为在这一阶段,边坡面已形成自由面,爆破波传来时有足够的自由震荡空间,当边坡坡面振动速度超过岩体承载临界值时即发生破坏。
3.1.2 动静耦合稳定性分析
目前深孔台阶爆破法已经成为露天矿生产爆破的主要方法。边坡体自由面较大,在动力扰动下振动波在坡面极易产生反射。边坡上覆岩体剥离之后形成高陡边坡体,形成的临空面越高其危险系数也越大。随着生产装药量不断增加,边坡体承受的动力扰动强度也随之增大,其稳定性面临严峻挑战,故有必要对动静耦合作用下的边坡体动力响应规律进行研究。为了考虑整个边坡体的应力场影响,动力分析时需要建立完整模型。如果爆破载荷依据实际的炮孔尺寸进行施加,则炮孔尺寸与边坡尺寸相差较大,不利于模型构建以及网格划分,因此需要将单孔装药等效为裸露药包模型。由于边坡上方生产工作已经结束,上部边坡即为最终边坡,根据模型设定将裸露药包置于露天坑最底部。本次分析的药包尺寸为100 cm×100 cm×20 cm(长×宽×高),等效药量为250 kg。由于动力稳定性分析过程中爆破载荷要与边坡体地应力耦合,故列出应力云图进行对比分析。将隐式分析结果导入LS-DYNA软件后的应力云图存在细微差异,主要原因是因为计算原理不同,但边坡体整体应力分布保持了较好的一致性,故在爆破动力分析中通过显式—隐式转换导入地应力的方法是可行的。
药包起爆时刻设定为0时刻,起爆后能量以波的形式向岩体内传播(图6)。由于药包附近岩体表面较为平整,故爆破应力波以同心圆弧的形式向下传播。当应力波遇到下边界及右边界时,受无反射边界条件影响,应力波在此界面发生透射。另一侧应力波沿介质传递,药包近区岩体处于高应力加载状态。另一方面,边坡体坡顶、平台与坡面均为自由面,应力波传播到上述位置将发生分散并叠加,故后续应力云图出现不规则波动。随着应力波继续传递,能量逐渐耗散。为定量研究边坡体受爆破载荷的影响,对台阶边界单元的应力时程响应结果进行了监测,单元位置如图7所示,各监测单元标高自上而下依次为+205、+135、+60、+50、+35 m。

各单元应力—时程曲线如图8所示。分析图8可知:距离药包最近的86709单元率先发生响应,其应力值比其它4个单元高。86709单元动力响应不同于其他单元,故需进行单独监测。随着卸荷状态起步,86709单元初始应力为0.938 MPa,受到爆破应力波作用后应力迅速下降,直至应力方向改变为Y反向。此后应力值发生波动,在7 190 μs时刻应力绝对值达到峰值40.8 MPa,此后应力波不断震荡并衰减。所有单元都是在初始应力影响下发生动力响应,在爆破应力波影响下呈现卸荷状态。各监测单元的应力极值如表4所示。
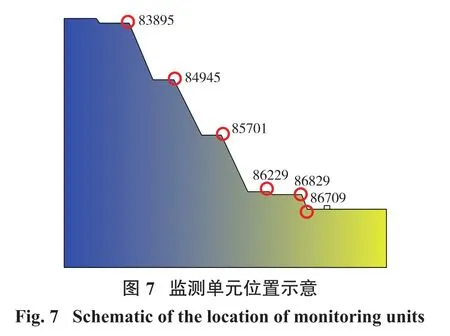


结合表4分析可知:最远两个单元相距50 m,应力极值随着影响距离的增加而减小,最远的84945单元的应力极值仅为1.9 MPa。从响应程度分析,爆破对边坡的影响主要集中在86829单元所在台阶。由于药包是裸露安放,因此初始爆破能积蓄较小。
对边坡体响应分析的依据,除了有效应力监测结果外,也可采用质点振动速度来衡量。坡面及台阶均为自由面,故振动比较明显,本研究主要从质点振动速度变化来分析,对5个关键节点的振动速度进行监测,监测点位置如图9所示。

各测点的最大振动速度监测结果如表5所示。由表5可知:该当量药量测点振动速度极大值均高于安全规程规定范围。测点上边界及右边界均为自由面,属于典型的卸荷自由面。应力释放后该位置应力值较小,质点具有相对自由的响应空间。测点振动速度较高,其原因除了炸药量较高外,监测点位于边坡顶部自由面,应力波反射作用较强也是关键因素。实际生产中,边坡开挖过程经历长时间卸荷作用,特别是坡顶位置岩土体处于松散状态,当受到爆破振动影响时,边坡坡面经常有砂石滚落。

根据应力以及测点振动速度综合分析可知,边坡体总体稳定性较好,受爆破动力影响,坡顶位置质点振动速度较大,生产中易掉落碎石,需重点防范。随着节点位置变化,爆心距也在增加,若在完整岩体中,距离爆源位置越远,爆破能量逐渐衰减,质点振动速度随之下降。在工程实践中,爆破引起的质点振动速度会随着测点与爆心高程差的增加而增大,这一现象称之为高程放大效应。这种效应受多方面因素控制,比如岩土体完整性、不良地质构造、爆破规模等。正常情况下,质点振动速度与爆心距、高程、开挖深度呈反比关系。高程放大效应也具有一定范围,超过这个范围就会消失,恢复正常状态。X方向振动速度监测结果显示,28592点位小于28576点位,对于Y方向振动速度,28599点位小于28592点位,这就是典型的高程放大效应,说明本研究仿真分析结果具有可靠性。通过动静耦合分析可知,爆破振动效应与坡度大小紧密相关,在过爆心的坡面、边坡、坡面角平分线围成的区域内较为明显。如果坡度大于1∶2,高程放大效应才会出现,坡面的自由反射作用也会影响坡体的振动频率。
3.2 边坡动力响应规律
上述分析仅对固定药量作用下的边坡体动力响应规律进行了分析,在实际生产中每次爆破量均不相等,故有必要对不同药量爆破作用下的边坡体动力响应规律进行研究。采用的计算方法仍为考虑地应力作用的显式—隐式转换法,共设定4组模型,如表6所示。图10所示为不同药量下的边坡塑性变形情况,随着药包药量增加,塑性区范围不断增大,不同方案对应的塑性区尺寸见表7。

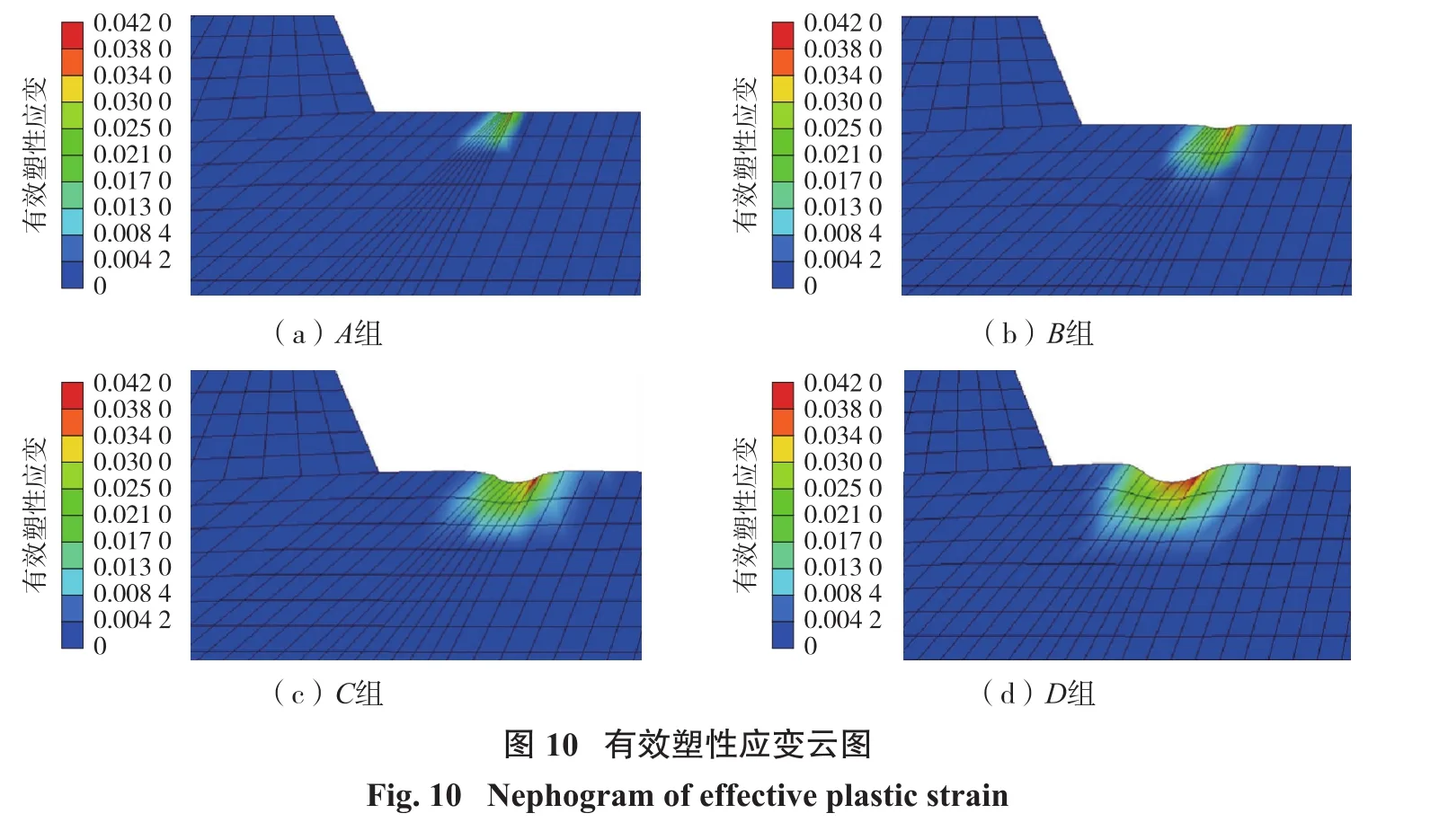

塑性区范围对应于实际生产中的爆破漏斗,由于上部为自由面,爆破漏斗呈现出的水平尺寸大于竖直尺寸的特征。随着装药量增加,水平方向塑性区增幅远大于竖直方向。根据网格变形幅度也可以看出,后两组模型呈现出明显的“凹坑”,且“凹坑”两侧受到挤压有轻微凸起,说明起爆药量控制着爆源附近的岩石破碎范围。4组模型监测同一位置单元的位移—时程曲线如图11所示。
由图11可知:单元变形发生在初始应力作用的基础上,当爆破应力波传至单元后,单元迅速产生较大形变,曲线第1个上升阶段对应爆破动力主导下的变形阶段。由于岩石材料是弹塑性材料,上述单元变形量大部分超过弹性形变的极值,呈现出一定的塑性变化。而大药量爆破动力加载过后的单元位移维持在一个特定水平发生波动,这一阶段的变形是衰减后的爆破动力与地应力共同作用的结果。对于药量最小的A组模型,距离爆源较远单元的初始动力响应表现为小范围变形,随后变形量才产生大幅度波动,说明小药量药包对远处单元影响较小,主要是提供扰动后作用。
不同药量方案单元位移结果如图12所示。由图12可知:随着监测单元与药包距离增加,位移呈减小趋势。起爆药量越大,该趋势愈加明显,说明单元位移受药量影响较大,这与上述分析一致。同一单元的位移也会随着起爆药量增加而增加。当爆心距持续增加,不同药量方案的单元位移差距越来越小。因此,单次起爆药量是影响边坡稳定性的主要因素之一,最佳的起爆药量不仅能保证起爆时的边坡稳定性,又能确保矿山采剥生产高效进行。药包破碎范围主要为药包下方半圆形区域,距离坡底25 m。随着起爆药量增加,药包近区单元位移不断上升。药包截面尺寸为150 cm×150 cm时(药量562.5 kg),爆源近区单元位移约为药包截面尺寸为200 cm×200 cm(药量1 000 kg)下的1 /2。药包药量增大则破碎范围增大,随之而来的爆震危害也更明显。药量过大也会造成爆源附近的碎石飞散,不利于装运。


为减轻爆震危害,应当尽可能维持最优药量爆破,且炸药选型应选取爆速较低、威力较小的炸药。当炸药量较大时,尽可能分散布置到多个炮孔中,采用分段微差起爆方式。爆破作业时,应注意边坡上部滚落碎石。当起爆点附近有重要构筑物时可采用预裂爆破形成预裂缝,削弱爆破振动对构筑物的影响。
4 结 论
本研究运用AUTO CAD与ANSYS联合建模技术建立高陡边坡动静耦合分析数值模型,采用ANSYS静力隐式计算方法得到边坡剥离后的地应力分布规律,将其导入LS-DYNA软件中进行显式动力分析,有效还原了地应力迁移环境下的爆震传播效果,实现了显式—隐式转换下的高陡边坡动静力学耦合分析,得出如下结论:
(1)动静耦合的计算模式有效还原了高陡边坡的初始应力,上覆岩层剥离后边坡体坡面及台阶位置发生卸荷力学行为,单元变形产生小范围回弹,使爆破应力波作用均在应力重分布的基础上开始响应。在这一计算模式下,边坡面成为了应力波传播的自由震荡空间,当振动速度超过其临界值时即发生破坏,实际生产中坡顶易发生碎石滚落,需重点防范。
(2)对显式—隐式联合计算结果进行塑性变化分析发现,炸药量越大,塑性范围随之呈正比增长关系;爆心距较小的单元动力响应过程始于爆破引发的大变形加载阶段,随后在爆破动力与地应力耦合作用下持续震荡直至平稳。通过对不同起爆药量下的质点振动速度及单元位移分析,确定药包尺寸为150 cm×150 cm×20 cm为安全高效生产的最优装药参数。
(3)根据不同药量爆破动力强度分析,提出了减震降灾措施:当炸药量较大时,尽可能分散到多个炮孔中,采用分段微差起爆方式;有爆破生产时,应注意边坡上部滚落碎石。当起爆点附近有重要构筑物时可采用预裂爆破形成预裂缝,削弱爆破振动对构筑物的影响。显隐转换分析方法有效实现了地应力影响下的爆震传播规律研究,但分析中对边坡坡体内的不良地质体考虑有限,在今后研究中通过融合节理的精细化建模方法,能够更好地实现仿真效果。
