预应力配筋率对节段拼装桥墩力学性能影响分析

2021-10-20刘铭炜

广东土木与建筑 2021年9期

刘铭炜

（广东省交通规划设计研究院集团股份有限公司广州 510507）

0 引言

节段拼装桥墩构件在厂区预制，相对于一般现浇桥墩质量更容易保证，且施工现场仅需要进行组装工作，因此特别适合在海上施工平台上进行跨海大桥的施工，或者在交通繁忙的地区进行高架桥施工［1］。

节段拼装桥墩根据连接方式不同，主要分为卯榫连接、现浇湿接缝连接、预应力连接等。其中预应力连接的节段拼装桥墩耗能能力强，且震后自复位能力也较高，能充分发挥高强钢绞线的作用。因此对于节段拼装桥墩，在承载力满足要求的情况下，采用预应力体系是比较合理的［2］。

目前国内的研究主要针对预应力节段桥墩的接缝受力性能、滞回性能、耗能能力等方面。如在1999年，田琪等人［3］通过试验研究了拼装式双柱桥墩盖梁与墩柱间的插入式接头和预应力接头的承载能力与滞回特性。2008 年，刘丰［4］对节段式、承插式、现浇式预应力桥墩的破坏机理进行了研究；2014 年，刘鑫［5］对预应力节段拼装桥墩的抗震性能进行了研究，探讨了预应力节段拼装桥墩力学性能的评价标准。

与国内的研究相比，国外研究更注重新型连接构造或者新型材料的研究；如2004 年，美国德克萨斯州大学的BILLINGTON 等人［6］发现加入了钢纤维混凝土后，能显著增加节段拼装桥墩的抗震性能；2007年，新西兰学者PALERMO 等人［7］给出了耗能钢筋和预应力钢筋的最佳用量比，同时验证了该种设计方法的正确性。2008 年，韩国学者KIM 等人［8］发现在接缝处采用合适的剪力键可以减小节段拼装桥墩的残余位移。

综上所述，当前的研究多是针对预应力节段拼装桥墩的抗震性能，如滞回性能、自复位能力、耗能能力等。但对于预应力节段拼装桥墩来说，预应力钢筋是最关键的构件，其配筋率对结构的力学性能影响的研究并不多，这给预应力节段拼装桥墩的设计带了很大阻力。

为了研究预应力配筋率对节段拼装桥墩力学性能的影响，本文首先以2015年高聪［9］做的静力试验桥墩为基础，控制预应力产生的轴压比为0.2，以预应力钢筋的配筋率为变化参数，设计3 种模型。然后利用ABAQUS 分别还原文献［9］的静力试验桥墩，以及文献［4］的拟静力试验预应力桥墩，将数值分析结果与文献中的试验结果进行比较，从而证明预应力节段拼装桥墩建模方法的合理性。最后基于上述模型，研究不同的预应力配筋率对节段拼装桥墩力学性能影响。

1 数值模拟方案设计

文献［9］对节段拼装桥墩进行静力加载试验，对不同接缝构造对节段拼装桥墩的力学性能的影响进行了研究。试件的具体尺寸构造如图1所示。

图1 试件尺寸以及断面配筋Fig.1 Reinforcement Layout and Structure （mm）

在上述试验模型的基础上，控制预应力引起的轴压比恒为0.2，以预应力配筋率为变化参数，分别设计3 种方案，并命名为PSC-1～PSC-3。PSC-1～PSC-3 的预应力配筋率分别为0.17%、0.34%、0.51%。预应力钢筋采用极限强度为1 860 MPa 的高强度钢绞线，各方案配筋如图2所示。

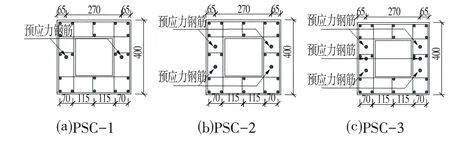
图2 方案配筋示意图Fig.2 Scheme Reinforcement Layout （mm）

在静力推覆加载之前，首先在墩顶施加竖向荷载300kN。然后在水平方向进行逐级加载来模拟静力推覆过程。静力推覆加载采用位移来控制，逐级加载过程如图3所示。

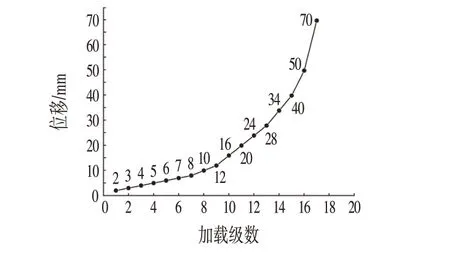
图3 逐级加载过程Fig.3 Step by Step Loading Process

综上，3个方案的参数如表1所示。

表1 方案名称及其特点Tab.1 Scheme Name and Its Characteristics

2 模型建立与验证

2.1 有限元模型建立

根据文献［10-13］，ABAQUS 中的损伤塑性模型可以较好模拟出混凝土的损伤演化，无论是在拟静力加载还是静力加载上，都具有较高的精度。故本文的混凝土本构采用损伤塑性模型。损伤因子以及本构曲线的定义参考《混凝土结构设计规范（2015 年版）：GB 50010—2010》。普通钢筋以及预应力钢筋均采用理想弹塑性模型来模拟。

预应力采用降温法［14-15］进行施加。钢束与锚具绑定（Tie）在一起，忽略两者间的相对滑移。钢束与混凝土间采用ABAQUS 中自带的Embed 约束，Embed约束可以自动考虑混凝土与钢束间的粘结力。有限元模型如图4所示（以PSC-1为例）。

图4 PSC1有限元实体模型Fig.4 PSC1 Scheme Finite Element Entity Model

2.2 方案模型验证

2.2.1 节段拼装桥墩建模方法的验证

利用上述方法建立文献［9］中的无预应力节段拼装桥墩试验模型，墩顶荷载-位移曲线结果对比如图5所示。

图5 荷载-位移曲线对比Fig.5 Comparison of Load-displacement Curve

由图5可知，在刚度和极限承载力上，计算值均大于试验值，这是由于Embed 约束忽略了钢筋与混凝土之间的滑移现象而引起的。同时可以发现，有限元计算结果曲线在极限承载力处存在尖点，这与试验的“脆性破坏”相吻合。

进一步提取极限承载力、极限位移、弹性极限位移3个参数，如表2所示。

表2 参数提取Tab.2 Parameter Extraction

由表2可知，在总体受力上，有限元计算结果与试验结果较为接近，可以满足工程精度要求。

除了总体受力满足精度要求，还需要在局部应力的分析上满足一定精度要求。根据文献［9］中的试验结果，本文提取对应特征位移点塑性应变云图如图6所示。

图6 模型塑性应变Fig.6 Plastic Strain

由文献［9］中的桥墩试验结果概况可知，当位移达到3 mm 时，底节段角部开始出现裂缝，位移达到24 mm时结构底节段出现斜裂纹。

由图6 可知，当加载位移达到3 mm 时，桥墩的塑性应变率先出现在底节段角部附近，当位移加载到24 mm 时，可以观察塑形应变以底节段角部附近为中心，斜向上扩散，与试验现象相符。

综上所述，无论是从总体的受力性能，还是从局部应力的分析上看，精度均可以满足要求。

2.2.2 预应力结构建模验证

文献［4］对预应力节段拼装式桥墩进行拟静力试验。本文选择该试验中的S3构件（有粘结现浇预应力桥墩）作为建模验证对象。构件的尺寸构造以及配筋如图7所示。

图7 试件构造配筋Fig.7 Reinforcement Layout and Structure （mm）

加载方面，该试验采用混合位移控制加载，每级进行3 次循环，加载初期幅值分别为2、3、5、7、10，然后位移幅值从20 开始，按照5 的增量每级进行递增，即幅值为20、25、30……，直至试件强度下降至承载力的85%，加载结束。

建立的有限元实体模型如图8所示。由于试验的加载幅值过多，为了提高计算效率，同时又能展现出模型的滞回特征，通过试算最终选取了位移幅值分别为3 mm、7 mm、10 mm、15 mm、20 mm、35 mm、50 mm、65 mm及70 mm，且每个幅值仅循环1次。

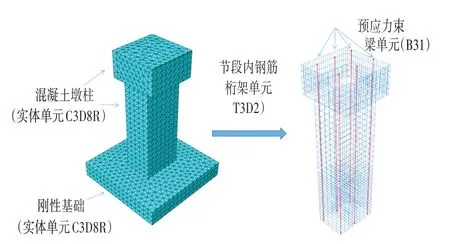
图8 有限元实体模型Fig.8 Finite Element Entity Model

对模型进行拟静力分析，可以得到结构的荷载-位移滞回曲线，有限元模拟计算得出的滞回曲线与试验结果的比较如图9所示。

图9 滞回曲线比较Fig.9 Simulation and Text Results of Hysteresis Curve

从图9可以看出，在加载初期，有限元计算得出的滞回环重叠且集中，呈现尖梭型，与试验值较为吻合。当位移幅值增大到至15 mm 时，结构的滞回环开始张开，承载力稳定上升，滞回环呈现仿锥形。当幅值加载到65 mm 时，结构正反向均达到极限承载力，正反向极限承载力为220 kN，与试验值的225 kN 较为吻合，相差仅为2%。由于试验过程中存在钢筋的滑移，因此试验得出的滞回曲线具有明显的捏缩效应，但数值分析模型却并未考虑钢筋的滑移作用，因此计算得出的下降段没有捏缩效应，导致卸载刚度存在偏差。

总的来说，计算所得的滞回曲线的总体形状与试件试验所得的滞回环总体形状较为相似，计算值在加载初期的刚度、侧向承载力、总体形状3个方面都表现出一定的精准度。数值分析得出的骨架曲线与试验结果对比如图10所示。

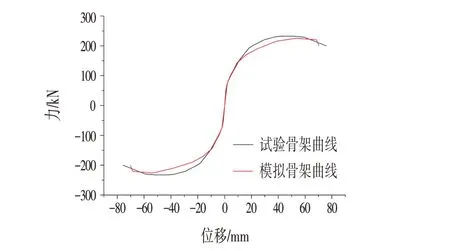
图10 骨架曲线比较Fig.10 Simulation and Text Results of Backbone Curves

从图10 可以看出，模拟骨架曲线与实验骨架曲线在加载初期拟合较好。但随着塑性的开展，两者差距逐渐拉大，计算值较实验值小。虽然模拟的极限承载力较为接近，但模拟的极限位移偏大。这是由于分析采用本模型的损伤因子的的计算取自于《混凝土结构设计规范（2015年版）：GB 50010—2010》中，是偏保守的值，而实际结构损伤值小于规范计算值，导致数值分析计算得出的结构偏“柔”。两者的骨架曲线虽有差异，但总的来说，该模型计算得出的骨架曲线与试验值比较吻合。

3 预应力配筋率对结构力学性能影响

利用上述方法建立PSC-1～PSC-3 模型，分析预应力配筋率分别为0.17%、0.34%、0.51%时节段拼装桥墩的力学性能。

3.1 变形和破坏模式

PSC-1～PSC-3 模型在达到极限承载力时的混凝土塑性应变如图11所示。

从图11可以发现，当预应力配筋率从0.17%增大到0.34%时，混凝土的受拉塑性应变范围大大缩小，但当配筋率从0.34%增大到0.52%时，其受拉塑性应变范围没有明显变化，证明预应力配筋率在0.34%范围内时，增大预应力配筋率可以有效减少塑性拉应变的范围，减小裂纹的分布范围，当预应力配筋率增大到0.34%时，再增加预应力配筋率对混凝土的塑性拉应变分布范围影响很小。预应力配筋为0.34%和0.51%的构件在破坏时仅在接缝两侧混凝土处产生塑性应变，结构破坏时裂纹将集中于胶接缝附近。且由应力云图可知，3 个模型的混凝土压应变均接近或大于混凝土的极限压应变（0.003 3），故结构在破坏时，受压区混凝土均有压碎现象。

图11 混凝土塑性应变云图Fig.11 Concrete Plastic Strain Magnitude

3种模型的普通钢筋以及预应力钢筋的屈服分布如图12所示。当数值达到1时证明钢筋完全屈服，其中红色部分表示完全进入屈服阶段的钢筋。

从图12 中可以明显观察出，3 种模型均仅有底节段中的普通钢筋屈服，预应力钢筋并未屈服。增大预应力配筋率对普通钢筋的屈服情况及其应力影响极少，从图12中可以观察到2种模型普通钢筋的屈服分几乎没有变化。

图12 普通钢筋屈服分布Fig.12 Steel Yield Distribution

3.2 荷载位移曲线

PSC-1～PSC-3 共3 种预应力配筋率下的桥墩模型的荷载-位移曲线对比如图13所示。

图13 位移荷载曲线比较Fig.13 Simulation and Text Results of Backbone Curves

3 种预应力配筋率的结构在弹性阶段时其荷载-位移曲线几乎重合，证明提高预应力配筋率对结构在弹性阶段的侧向刚度影响很小。在进入塑性阶段后，可以明显发现预应力配筋率为0.17%（PSC-1）的结构存在一段屈服平台，当预应力配筋率提高到0.34%（PSC-2）或0.51%（PSC-3）后，结构的屈服平台消失，结构在达到极限承载力时出现了“持载”现象。预应力配筋率为0.17%的结构其下降段比较平滑，承载力稳定下降，当将预应力配筋率增大到0.35%或0.51%后，下降段出现了较明显波动，预应力配筋率越大波动越明显，该现象说明预应力配筋率为0.35%或0.51%结构在丧失承载力的同时却具有反复抗力的能力，具有更强的耗能能力。同时可以发现，预应力配筋率越大，结构在达到极限承载力后，其承载力丧失的速度也越快。