基于KNN 算法的隧道地表变形监测数据异常检测分析
2021-10-20邹彤彤王仲平余来斌王东凯出晓娟
邹彤彤 杨 涛 周 勇 王仲平 余来斌 王东凯 肖 荣 出晓娟
(1、兰州交通大学数理学院,甘肃 兰州 730070 2、中国科学院海西研究院泉州装备制造研究所,福建 泉州 362200 3、中国建筑第八工程局有限公司,上海 200000 4、中建八局有限公司南方公司,广西 南宁 530022)
1 概述
近年来,随着经济的高速发展,城市地下工程急剧增加,地面问题日趋严重。在隧道开挖中,由于受到地下复杂的地质工程条件、周边环境、突发灾害以及人为破坏等因素的影响,会产生渗漏水、裂缝、断面变形侵限、掉块、衬砌错台错缝、衬砌腐蚀劣化、冻害、震害、钢筋钢拱架锈蚀、道板隆起、拱顶坍塌等各种病害,造成人员伤亡及经济损失[1-2]。针对以上各种隧道病害,对隧道进行地表变形监测[3],了解场地地表及建筑物变形、沉降发展动态、规律,为场地地基稳定性鉴别和预测、预警提供依据是非常必要的[4]。但由于环境恶化,设备损坏等多种因素的影响,获得的监测数据中会存在很多与标准值(或期待值)有偏离的样本,也就是说与绝大部分数据“长的不一样”的样本,即异常值。传统的异常监测方法大多是由统计学界完成的,因其简单易操作等优点在工程领域得到了广泛的应用,如胡碧辉等[5]用3σ 准则和高斯过程回归相结合的方法对变形异常数据进行检测,李增良[6]用箱线图法对盾构地表变形数据进行异常识别。但这种基于统计学的检测方法主要是对数据做出一定假设,并找出在此假设之下定义的“异常”,因此往往会使用极值分析或假设检验,且可解释性弱,具有一定的局限性。随着数据收集技术的不断更新,基于数据挖掘的异常检测开始进入大众视野,并占据重要地位。各种算法开始广泛应用于异常检测中,K-均值聚类算法(K nearest neighbors, KNN)[7]算法因其简单高效等诸多优点得到了广泛的应用。
对于无数据标签的异常检测问题,本文提出了一种K 近邻算法的无监督异常检测算法,并用该算法对岑溪至水汶高速公路均昌隧道地表变形监测数据进行异常检测。
2 算法简介
K 近邻算法(K-Nearest Neighbor,KNN)是一种常见的分类算法,也常用于数据的异常检测问题中[8、9、10]。其基本思想是:给定测试样本,基于某种距离度量找到训练集中与待分类样本相似度最大的k 个训练样本,然后基于这k 个近邻样本的类别信息采用投票方式确定待分类样本的所属类别,如图1 所示,从内到外k 值分别取k=1,k=3,k=5。k 的取值决定了待测样本的类别,当k=1 时,待测样本为正类,k=3 时待测样本为负类,k=5 时待测样本为正类[11]。具体算法原理如下:
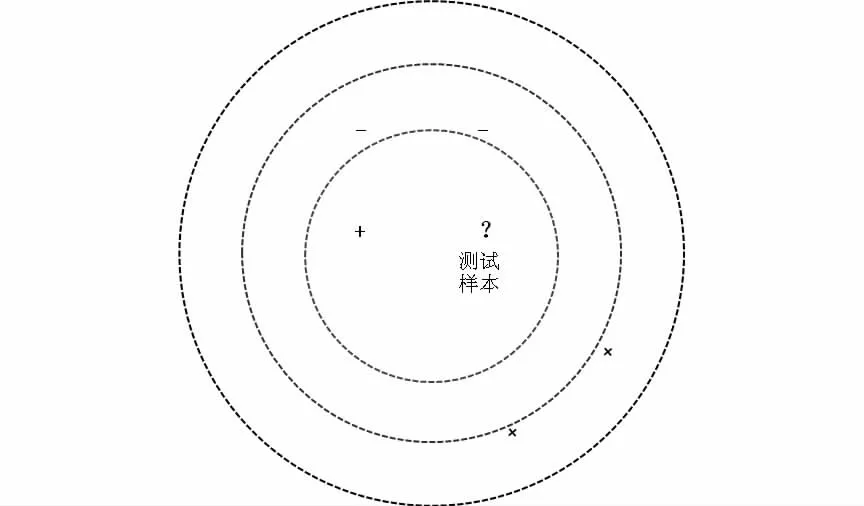
图1 k 近邻分类器示意图

式(1)中,I 为指示函数,即当yi=cj时I 为1,否则为0。
3 工程应用
3.1 工程背景
在建岑溪至水汶高速公路岑溪大隧道位于岑溪市岑城镇钓石村及大隆镇均昌村之间的崇山峻岭,设计为分离式小净距,净空(孔- 宽×高)为1-10.75×5m,左线桩号DK6+455~DK10+725,设计高程为316.92~304.48m;右线桩号DK6+477~DK10+765,设计高程为317.03~303.84m,为特长隧道。隧道穿越构造中低山地貌单元,地面标高250.00~806.00m,主要地层岩性为第四系冲洪积层粉质粘土、卵石、飘石等和残坡积层砂质粘土;下伏基岩为混合岩(片麻状花岗岩、片麻岩、石英岩等),分布有全风化、强风化、中风化和微风化层,见图2。地质构造稳定,地下埋藏浅,水量丰富。隧道中部从岑溪市岑城镇山心村下部穿过,村庄周围地面距隧道顶最小距离约90m,属于中低山剥蚀形成的小盆地,次生断层密集,周边汇水面积大,地表水塘及溪流密布,泉眼分布广,地下水赋存浅、丰富,地表水与地下水相贯通。居民生活、生产用水为地表泉水和溪流。地表大部分民房为土坯房或简易砖混房,浅基础或无基础,无圈梁或框架,地基土质松散,修建年代比较久,存在不同程度的原生裂缝。
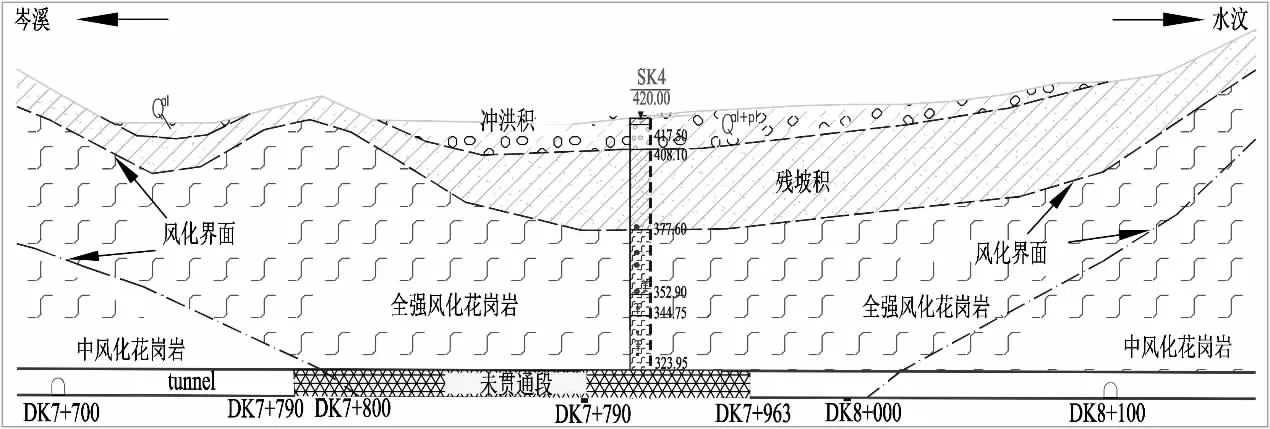
图2 均昌隧道地质剖面图
2013 年9 月11 日6:30 左右,正在开挖作业的右洞CK7+838 掌子面出现股状涌水,涌水口直径开始约15cm,随后增至80cm,初始涌水量约1000m3/h,最大突水量达1280m3/h,之后9 月12 日~21 日期间,涌水量保持700m3/h,累计涌水量达到25 万m3。同时,同时,灾害发生后,诱发地表塌陷、农田损坏、房屋开裂、地表水干涸等次生灾害,如图3。

图3 突水灾害及诱发地表灾害情况
为了了解场地地表及建(构)筑物变形、沉降发展动态、规律,为场地地基稳定性鉴别和预测、预警提供依据,在民房及道路基础顶面、墙角设置23 个监测点。剔除因环境干扰、监测误差等导致的数据异常,是保障数据可靠性的重要工作,见图4。
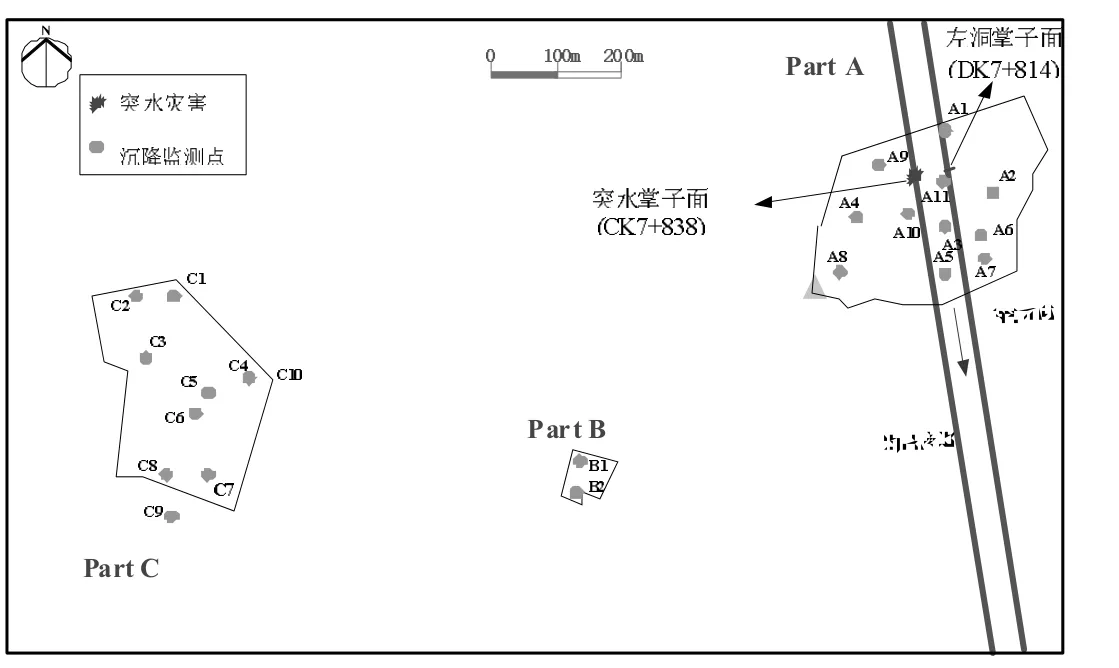
图4 沉降监测点布置
3.2 监测数据异常分析
用KNN 对每个监测点分别进行异常检测,检测结果如表1所示,大部分监测点的监测样本数均为62,在A 区异常占比最高的分别是A4 和A2,B 区中异常占比最高的是B1,C 区中异常占比最高的是C1,且从不同区域异常占比变化图(图5)可以看出,A 区的异常点主要分布在前五个监测点中,越往后监测效果越稳定。B 区中第一个监测点B1 异常占比为11.3%,相较于B1,监测点B2 的异常占比有明显的下降趋势,但由于该区所设监测点较少,且B2 中的异常占比与其他监测点相比也相对较高,所以在B 区域的监测点设置需进一步考察。C 区除第一个监测点存在大量异常点外,其余监测点的监测数据异常分布情况相对趋于稳定,监测点C3 和C6 处获得的监测点异常占比最低,仅占3.2%,相较于A 区,C 区异常占比在后面的监测点中有缓慢上升的趋势。
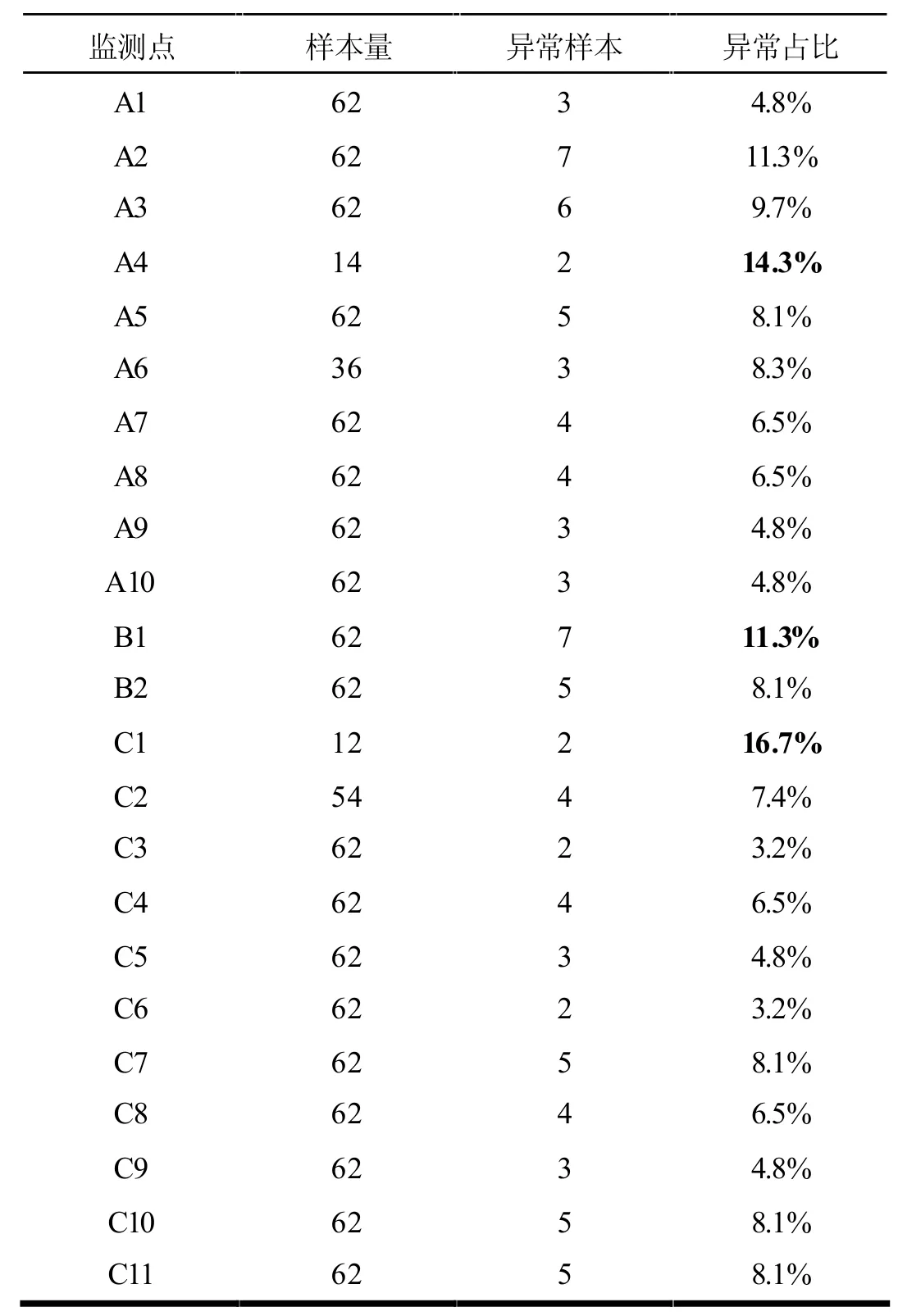
表1 各监测点异常值占比
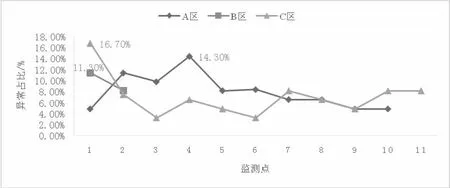
图5 不同区域异常占比变化图
4 结论
对于无数据标签的隧道地表变形监测数据的异常检测问题,本文提出了一种无监督式的k 近邻异常监测算法,该算法从全局领域的角度出发找出偏离数据整体趋势的点即异常点。将该算法应用于岑溪至水汶高速公路岑溪大隧道的地表变形监测数据中,对23 个监测点分别进行异常检测,并对不同区域的异常检测结果进行分析,发现A 区在监测点A9,A10 两个监测点上效果更稳定,C 区监测点C3 和C6 处获得的监测点异常占比最低。
