变转速下涡旋压缩机转子系统不平衡瞬态响应分析

赵 嫚，高汉根

(兰州理工大学石油化工学院，甘肃 兰州 730050)

1 引言

涡旋压缩机作为第三代压缩机与传统往复式、转子式、斜盘式、螺杆式压缩机相比具有体积小、效率和可靠性高、节能环保、对制冷液滴的容许度大、噪声小等特点。涡旋压缩机的优点显著，因此在多个领域被广泛应用[1]。随着涡旋压缩机朝着高转速、高压比和智能化方向的发展，转子动力学在转子系统结构设计、制造及运行过程中的作用愈加突出，因此对涡旋压缩机转子系统动力特性的研究尤为重要。

目前国内外在转子系统动力特性方面的研究主要有：苏亚锋等针对电机在高速运转时工作转速内易产生共振的问题，利用有限元法分析了临界转速[2]。赵嫚等通过对偏心套筒式径向随变机构研究得出该机构在减小回转半径方面的调节对压缩机转子系平衡的影响较大[3]。缪仲威等通过EXCEL软件提供的规划求解功能分析了动平衡系统的不平衡量对压缩机振动的影响[4]。顾文等通过理论分析和模拟仿真相互结合的方法对某电动涡旋压缩机在不同转速下的工况进行模拟，分析动平衡规律，为电动涡旋压缩机的优化提供支持[5]。张春等通过ANSYS软件建立了考虑轴承刚度、曲轴和动涡旋盘柔性的涡旋压缩机转子系统的刚柔耦合模型，得到了实际工况和理想工况时运动副反力，以及实际工况时曲轴和动涡旋盘的应力、应变情况[6]。P Flores，J Ambrósio等对含有运动副间隙的多刚体机构系统的动力特性进行了数值分析[7]。但是对转子系统启动加速到额定转速过程中的瞬态过程研究较少，并且由于转子的结构设计、材质不均匀等因素，特别是在机器启动时转子加速度变化较大的时候导致机器运转时转子系统失稳不平衡，会产生机械振动和噪声，加速轴承、轴封等零件的磨损，使机械寿命降低。同时瞬态不平衡响应分析更接近转子系统的实际工况，因此对转子系统进行瞬态响应分析尤为重要。

本文通过应用SolidWorks软件对某卧式涡旋压缩机转子系统进行建模；运用ANSYS Workbench软件对转子系统进行有限元分析，为保证涡旋压缩机转子系统高速平稳运行提供参考。

2 转子系统模态分析与临界转速计算

转子系统包括动涡旋盘、主轴承、副轴承、偏心曲轴、平衡铁和带轮组成，通过SolidWorks软件对转子系统各部件进行建模，并把建立好的模型导入Workbench中进行下一步分析。

2.1 转子系统气体力分析

转子系统所受气体力有轴向气体力Fa、径向气体力Fr和切向气体力Ft。其中切向气体力作用在动、静涡旋盘基圆中心连线的中心处，方向垂直于基圆中心连线。径向气体力方向由动涡旋盘指向静涡旋盘。

选定涡旋压缩机基本参数：

基圆半径r=3.5 mm，涡旋齿厚t=4.5 mm，涡旋齿高h=40 mm，排气角θ*=221°，压缩腔对数N=3。结合相关理论计算涡旋盘在排气角位置时的最大切向气体力Ft=810 N，径向气体力Fr=86 N。

2.2 设置仿真参数

在ANSYS Workbench软件中进行以下设定，首先定义转子系统各部件模型的材料属性如表1所示，然后在动涡旋盘处施加径向气体力86 N，切向气体力810 N，并通过轴承负载(Bearings Load)的方式将带轮预紧力861 N施加到带轮上[8]。在主、副轴承轴表面施加圆柱约束(Cylindrical Support)，同时设定限制径向、切向方向上的位移但释放轴向的自由度，并施加无摩擦约束(Frictionless Support)在轴承内圈处，最后采用远端位移约束(Remote Displacement)限制轴向方向的位移。

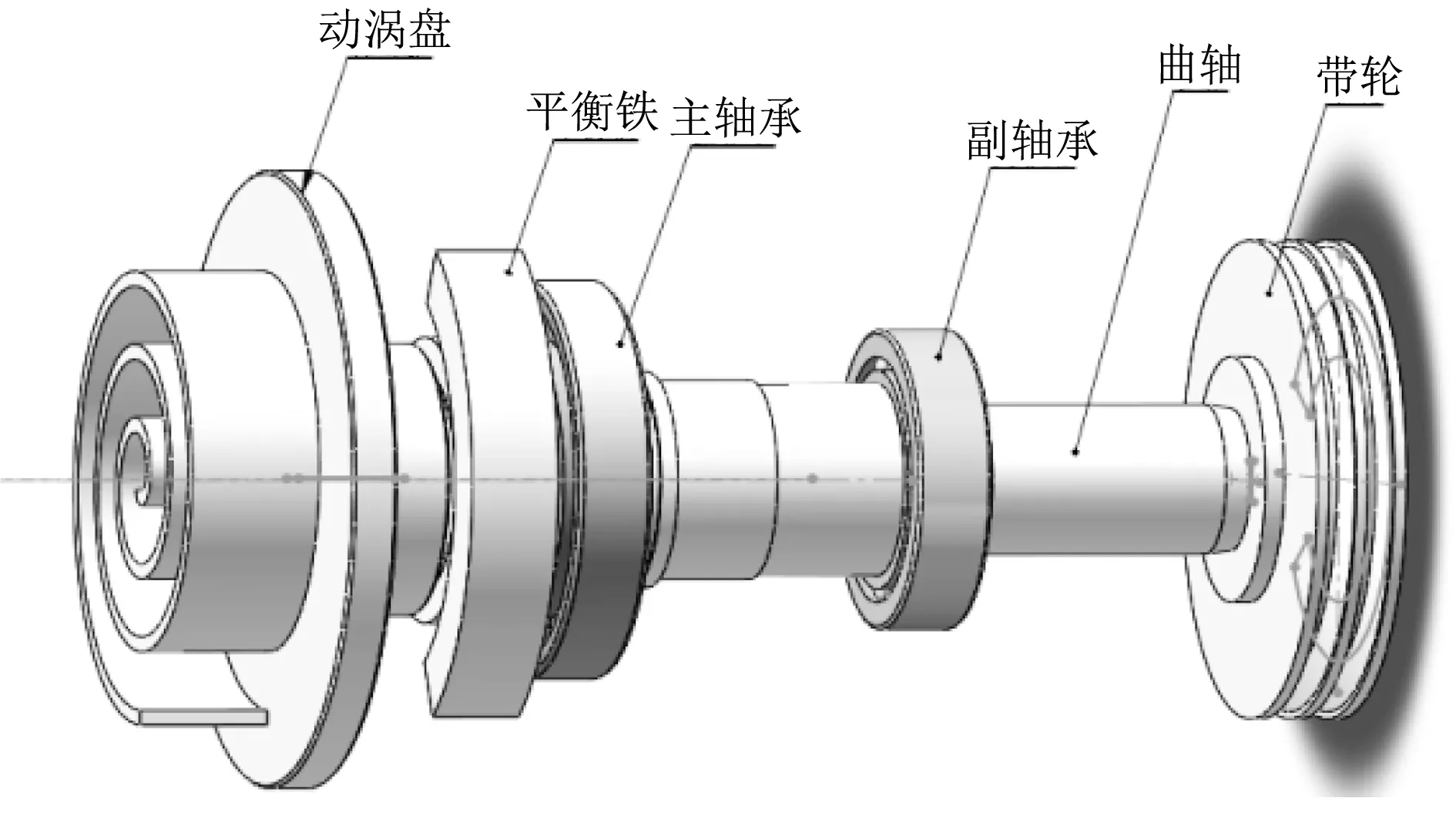
图1 转子系统三维模型

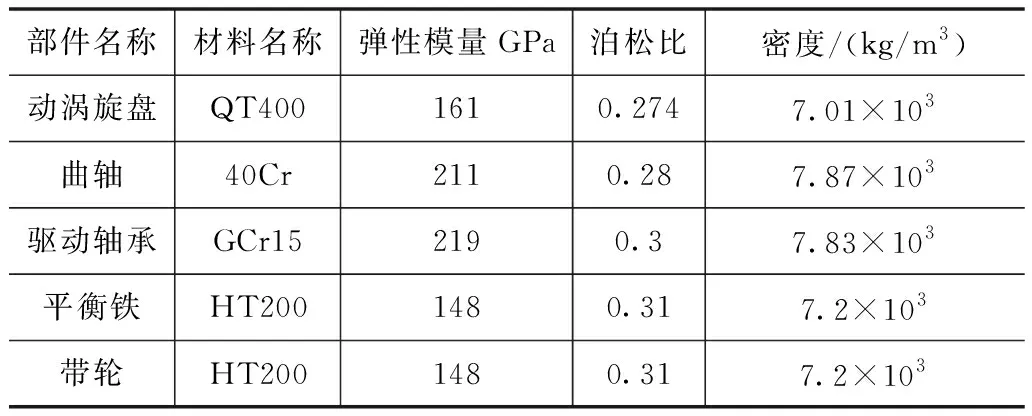
表1 模型材料属性

2.3 模态分析结果

考虑结构振动中高阶模态能量占比很低，对整个结构振动影响不大且一般载荷频率较低，所以只需要考虑前几阶模态是否会共振[9]，只取涡旋压缩机转子系统的前六阶模态。模拟得到了涡旋压缩机转子无阻尼自由振动状态下的前六阶固有频率和相应振型，分析结果见表2和图2。

表2 转子系统前六阶固有频率 单位：Hz

图2 涡旋压缩机转子前六阶振型

从图2和表2转子系统前六阶振型云图和前六阶固有频率可以看出：一、二阶模态固有频率分别为865.44 Hz、1077.6 Hz，振动形态主要是传动系统变形集中在尾部带轮端，说明这个部位容易发生振动；三阶模态，其固有频率为1079.3 Hz，振动形态主要为曲轴末端的弯曲振动；第四和第五阶的固有频率比较接近，分别为2689.4 Hz和2770 Hz，从图2(d)和(e)可以看出转子系统在此频率下产生弯曲振动，变形较大位置出现在平衡铁和曲轴中段；对于第六阶模态振型，其固有频率为2949.9 Hz，振动形态主要表现为平衡铁X-O-Y平面内弯曲。

2.4 临界转速计算

由于转动系统中转子各微段的质心不可能严格处于回转轴上，当转子转动时会出现横向干扰，在某些转速下还会引起系统强烈振动，出现这种情况时的转速就是临界转速。因此临界转速的计算尤为重要，可以借助坎贝尔图(Campbell Diagram)来判断转子工作时是否出现共振，以确定出现共振时的频率阶次和临界转速[10]。本次模拟计算进行以下设置：

设置旋转速度为0～6000 r/min，并考虑陀螺仪效应。采用远端位移约束(Remote Displacement)限制轴向方向的位移。

从图3所示坎贝尔图中可以看出，转子系统在0～6000 r/min额定工作转速范围内涡动线与各阶模态频率线没有产生交点，因此没有出现临界转速点，转子系统在工作转速范围没有出现共振，平稳运行。

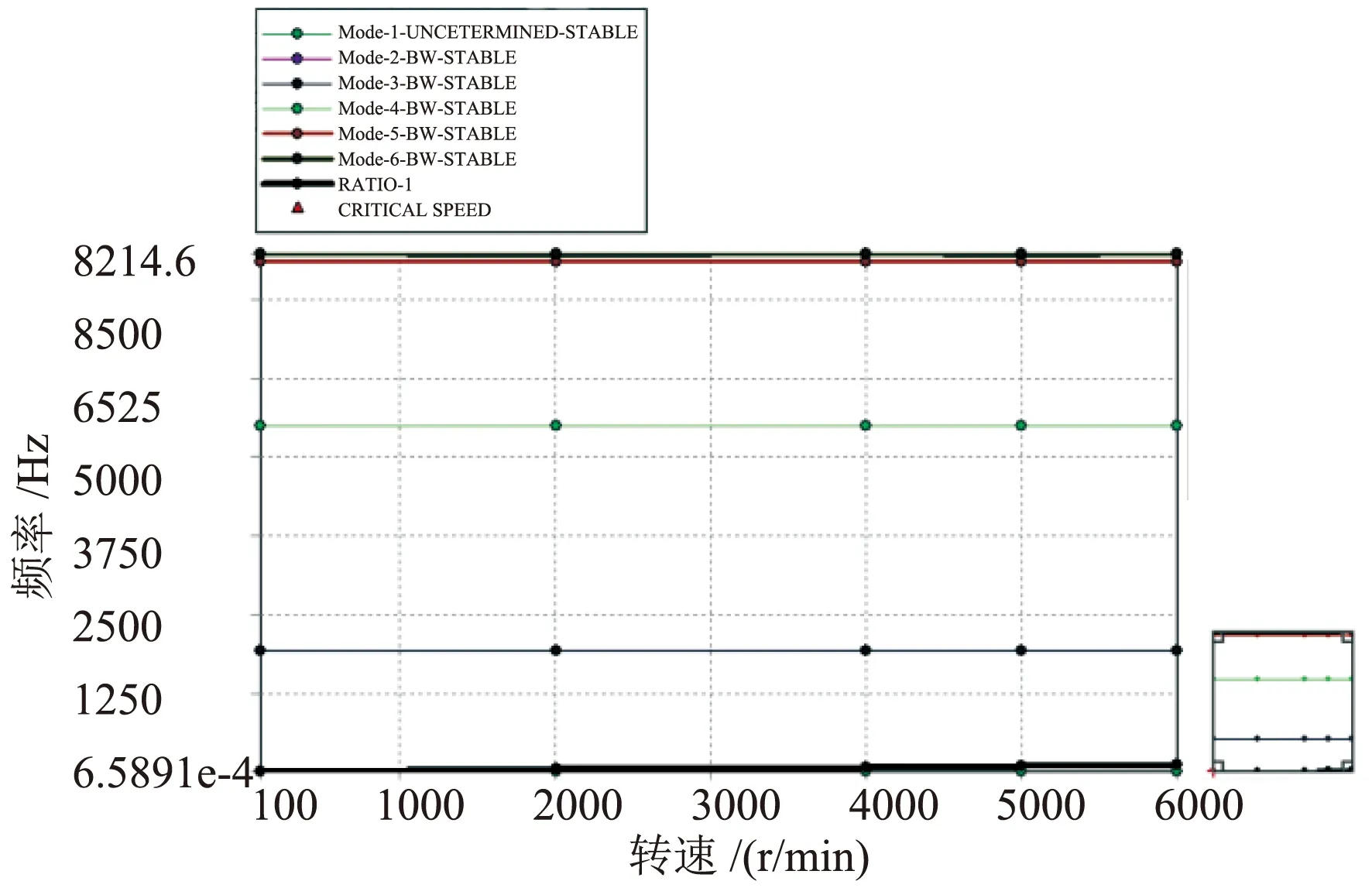
图3 转子系统坎贝尔图

3 瞬态动力学响应分析

瞬态动力学响应分析主要应用于转子在变转速工况下运行、不平衡质量以及外部载荷发生变化时转子的不平衡响应分析，相比于稳态情况瞬态分析更接近实际的运转情况。本文主要从前2个应用角度出发，以转子启动加速过程为例，模拟转子在5 s内转速从0～6000 r/min达到额定转速的加速过程的动力特性。由于不能直接添加不平衡力，因此可以把它分解为两个垂直方向的分量表示。如下

F=meΩ2

(1)

Fy=meΩ2cos(ωt)

(2)

Fz=meΩ2sin(ωt)

(3)

式中F——由不平衡质量产生的离心力，N

m——不平衡质量大小，kg

e——偏心距，m

Ω——旋转速度，rad/s

利用SolidWorks软件测得偏心距为0.072 m，夹角为15°。计算得到F=568 N。具体参数进行以下设定：

首先在转子系统两端添加固定约束，不平衡质量模拟为0.02 kg加载在动涡旋盘上，时间步长设置为0.05 s，并考虑陀螺仪效应，设置不平衡力的添加形式为函数形式Y轴方向设置为Fy=568cos(ωt)，Z轴方向设置为Fz=568sin(ωt)，周期为2π。提取转子系统整体变形随时间变化曲线图如图4所示。

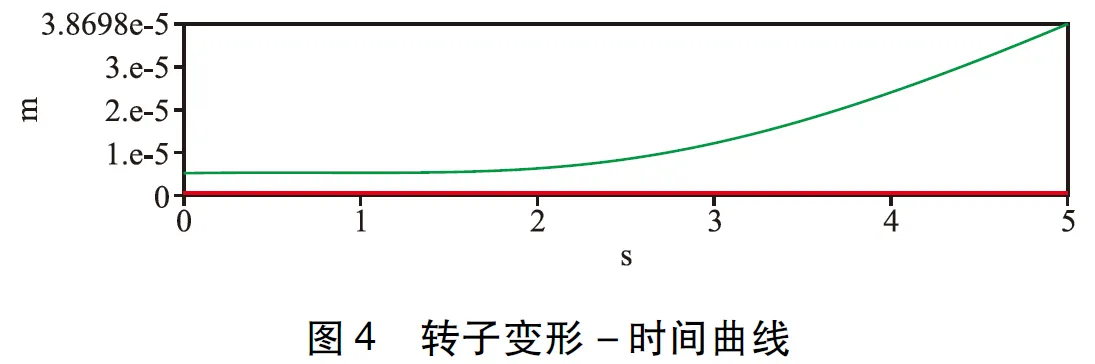
从图4中可以看出转子系统在0～2 s时变化不大，随着转速升高，转子系统在2～5 s变形逐渐增大，这主要是因为速度逐渐达到额定转速，转子系统所受不平衡力达到最大，最大位移出现在5 s处为3.8698e-3mm。为了观察转子在峰值时的变形情况，提取转子在5s处三维形变云图。

从图5中可以看出，转子系统最大变形处出现在了平衡铁处，这是因为平衡铁为非对称零件且偏心距最大，所受离心惯性力很大，符合实际工况。根据旋转机械标准振动评价等级ISO-10816，对比该转子系统的最大形变量3.8698e-3mm，可知变形量符合规定转子系统变形在可接受范围内。

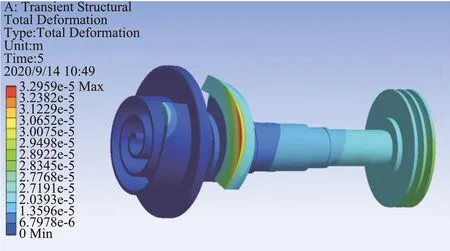
图5 转子5 s时变形云图

4 结论

(1)转子系统的前六阶固有频率及振型分析确定了转子系统的薄弱环节。

(2)转子系统在工作转速范围内未出现临界转速点，转子系统运行平稳不会出现共振情况。

(3)整个转子系统在额定转速内因不平衡质量产生的变形符合机械运行标准，在对整机影响在规定范围内。