环形微孔中钢针缩进量对中空纤维中空度和挤出胀大的影响*

杨崇倡 王佳林 冯 培, 2 汤文斌

1. 东华大学机械工程学院，上海201620；2. 浙江恒澜科技有限公司，浙江 杭州310000

中空纤维是一类沿其轴向呈管式空腔状的异形纤维[1]，空腔内的空气赋予异形纤维质轻、保温、高压缩回弹性、高蓬松性等特点。目前，中空纤维主要采用圆弧狭缝式喷丝板，经熔融纺丝或湿法纺丝工艺纺制而成。具有“C”字形和“品”字形微孔的圆弧狭缝式喷丝板的使用效果良好[2]。

中空纤维的中空度一般为15%，影响其中空度的关键因素包括微孔的结构与尺寸，纺丝温度和冷却条件等[3]。当圆弧狭缝式喷丝板的狭缝宽度较小时，聚合物熔体的挤出膨胀量小，成形中空纤维的管壁薄且空腔不能闭合[4]；狭缝宽度较大时，聚合物熔体挤出量大，成形中空纤维的空腔小。因此，需对现有中空纤维的纺丝工艺和相关装置进行改进，以制备能满足使用需求的中空纤维。于俊荣等[5]采用圆形微孔内置同轴圆形钢针的纺丝组件，加工出横截面为环形、中空度较大的中空纤维。该研究指出，在这一纺丝组件中，中空纤维的中空度随钢针缩进量的不同而发生变化。聚合物熔体离开圆弧狭缝式喷丝板后的挤出胀大比和中空纤维的中空度主要受喷丝微孔通道中聚合物熔体的黏性﹑弹性回复性及其流动状态的影响。钢针缩进量不同，熔体在微孔内的速度场、弹性回复性等流动特征则不同。

本文将利用Polyflow软件对聚合物熔体在圆弧狭缝式喷丝板微孔通道中的流动特征进行数值模拟，讨论熔体在微孔通道内的速度变化、挤出胀大反应及中空度变化趋势与钢针缩进量的关系，分析不同的钢针缩进量对环形或圆形微孔通道中聚合物熔体流速的影响，为今后能精确控制中空纤维的中空度提供参考。

1 微孔内熔体流动特征的数值模拟

国内外关于中空纤维的计算模拟成果颇丰，Ziabicki等[6-7]、Kase等[8]提出了纺丝过程中熔体流动的基本动量、连续、能量平衡三大控制方程。Freeman等[9]基于中空纤维纺丝动力学方程，研究了熔体在喷丝板微孔附近的流动情况。Oh等[10-11]通过有限元分析法建立了丙纶中空纤维熔融纺的动力学模型。但以横截面为环形的中空纤维为分析对象的模拟研究较少，钢针缩进量不同、环形微孔和圆形微孔通道同时存在时，熔体流动状态的模拟计算更少。本文将通过Polyflow数值模拟，分析钢针缩进量h不同时，各微孔通道内熔体的流动状态及所制备中空纤维的中空度，并与试验结果进行对比，验证模拟结果的准确性和模拟方法的可靠性。

1.1 理论模型的建立

鉴于熔体流动的复杂性和准确计量的难度，本文对熔体在圆弧狭缝式喷丝板微孔中的流动做如下假定[12]以简化模拟计算过程。

1) 纺丝组件中的熔体，黏度较大，雷诺数较小，呈等温平稳层流动。

2) 熔体为不可压缩非牛顿流体，其流动状态为蠕动流，流速较慢，流体的温度和压力与其密度相关性较低，流体所受重力与惯性力忽略不计。

3) 熔体与微孔通道的壁面不产生滑移，其流动控制方程如式(1)～式(3)。

连续方程： ∇V=0

(1)

(2)

(3)

式中: ∇——微分算子；

V——流体速度矢量，m/s；

ρ——流体密度，kg/m3；

τ——应力张量，Pa；

p——压强，Pa；

T——流体温度，℃；

Cp——定容比热容，J/(kg·K)；

q1——导热通量向量。

熔体在微孔通道内流动时的剪切速率较低，其运动特性符合Bird-Carreau本构模型[式(4)]。

(4)

式中:η∞——剪切速率无穷大时的极限剪切黏度，Pa·s；

η0——零剪切黏度，Pa·s；

λ——特征松弛时间，s；

n——非牛顿指数；

γ——空气密度，kg/m3。

本文以聚丙烯切片为纺丝原料，其熔融态的性能参数及模拟计算中的参数设置列于表1[13]，钢针缩进量h分别设定为0.00、0.05、0.10、0.15和0.20 mm 5种。

表1 聚丙烯熔体的性能参数和模拟参数设置

1.2 几何模型

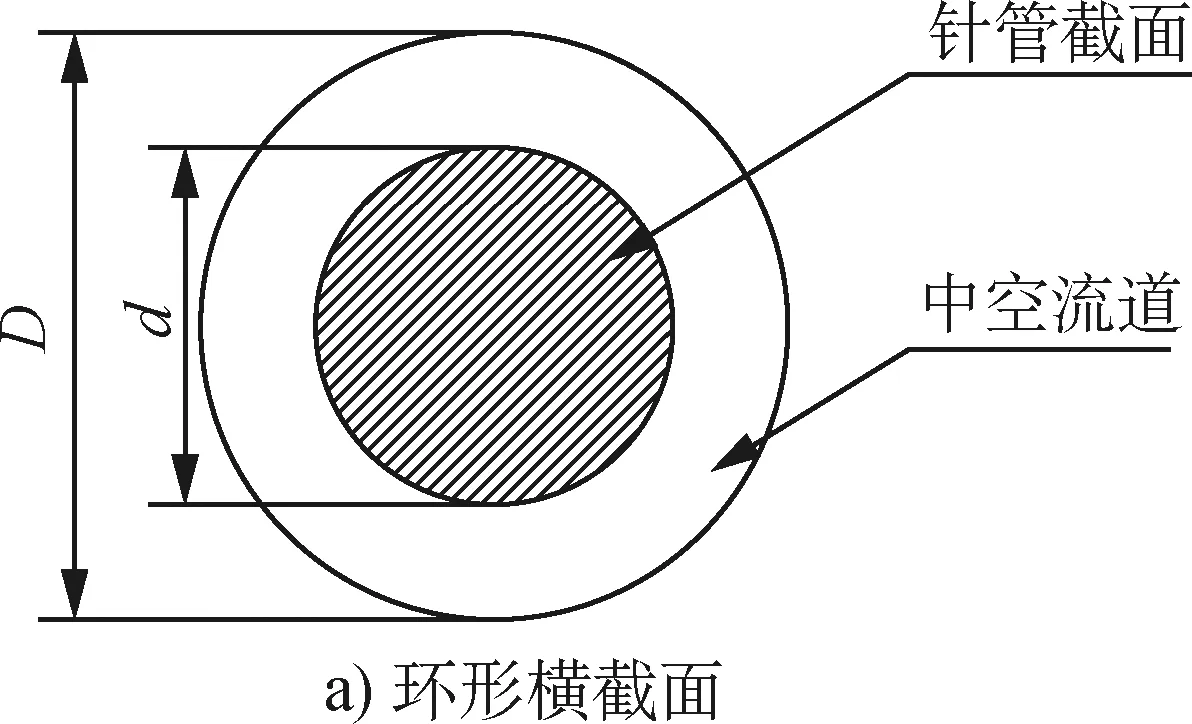
模拟中，首先根据聚丙烯切片的特性和试验条件设置模型的参数和边界条件，然后建立几何模型，最后采用有限元分析法得出聚丙烯熔体的非等温黏弹数值模拟结果，分析h不同时，聚丙烯熔体的形貌和流动特征，如流速分布、挤出胀大比及中空度等。

熔体的流道模型如图2所示。熔体在这一微孔通道内的流动主要分为A﹑B和C 3段：A段熔体在环形流道内的流动；B段熔体失去钢针壁面束缚后在圆形流道内的流动；C段纺丝细流离开喷丝孔向外挤出并凝固成中空纤维。

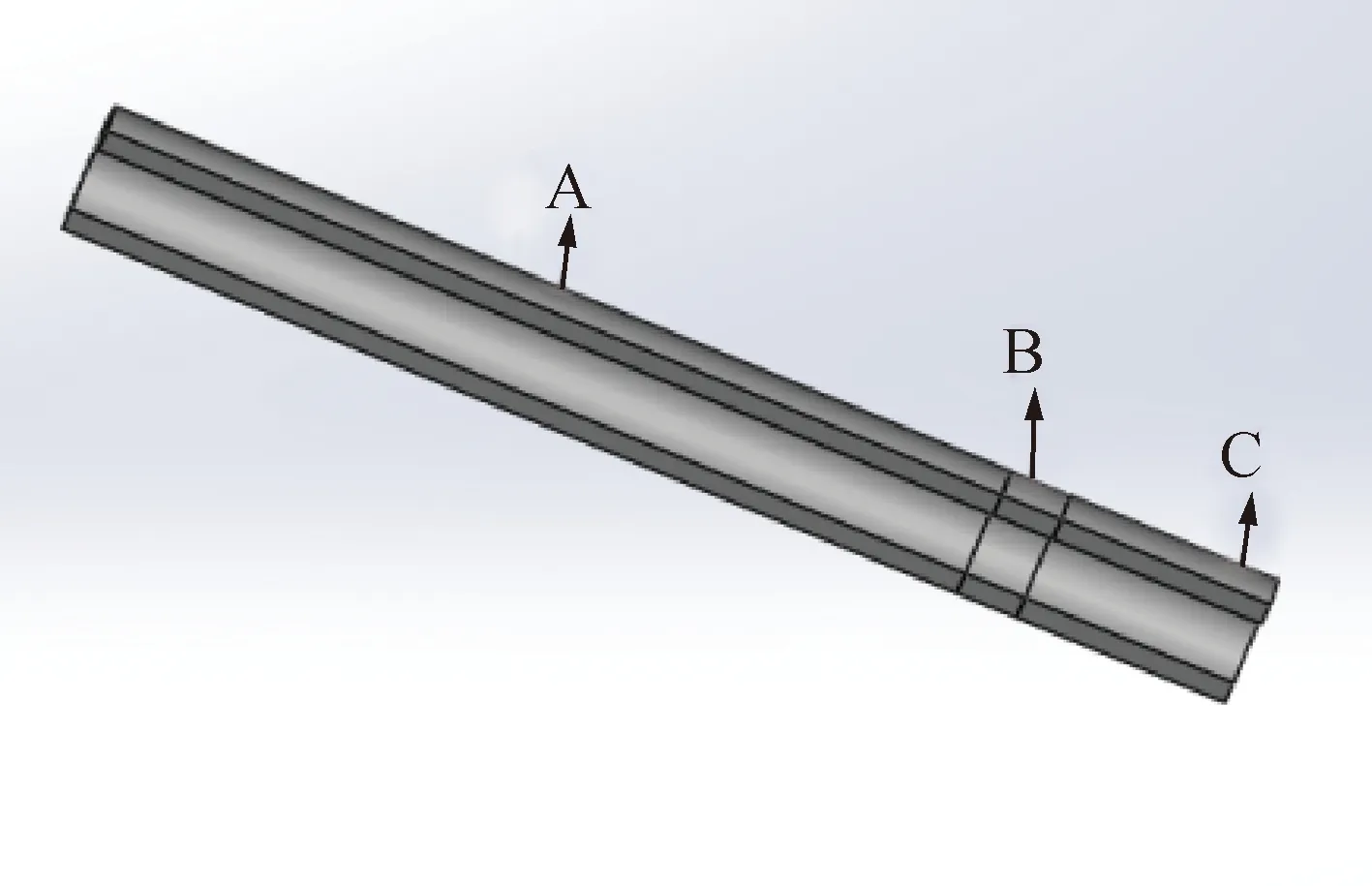
图2 熔体流动通道模型

为简化模型并减少计算时间，本文将B段分成两部分，然后分别组合到环形流段A和挤出段C中，从而将A、B、C段通道模型简化为壁面段F和自由段E两段模型(图3)。

图3 熔体流动通道的简化模型

利用Polyflow软件模拟得到熔体流动通道网格划分和边界划分模型(图4)。

1.3 边界条件设置

1)入口面：熔体在微孔入口处的流量q=4.4×10-9m3/s，温度为290 ℃。

2)壁面：熔体和纺丝组件内壁面不产生滑移现象，即法向速度和切向速度均为零，纺丝温度为290 ℃。

3)自由面：熔体的法向速度、法向应力与切向应力均为零。设置热对流交换，微孔外自由面的温度为20 ℃的冷却风温度，内自由面温度为290 ℃。

4)出口面：熔体受压离开喷丝板后其惯性力及重力忽略不计，流体的法向应力与切向应力均为零。

2 数值模拟结果分析

2.1 速度分布

熔体从圆形微孔挤出的过程中与孔壁面不产生滑移，挤出后产生的胀大现象是微孔内熔体流速分布变化的主要原因，主要表现在熔体径向流速的变化。钢针缩进量不同时，熔体在流道内的流动速度模拟云图如图5所示。

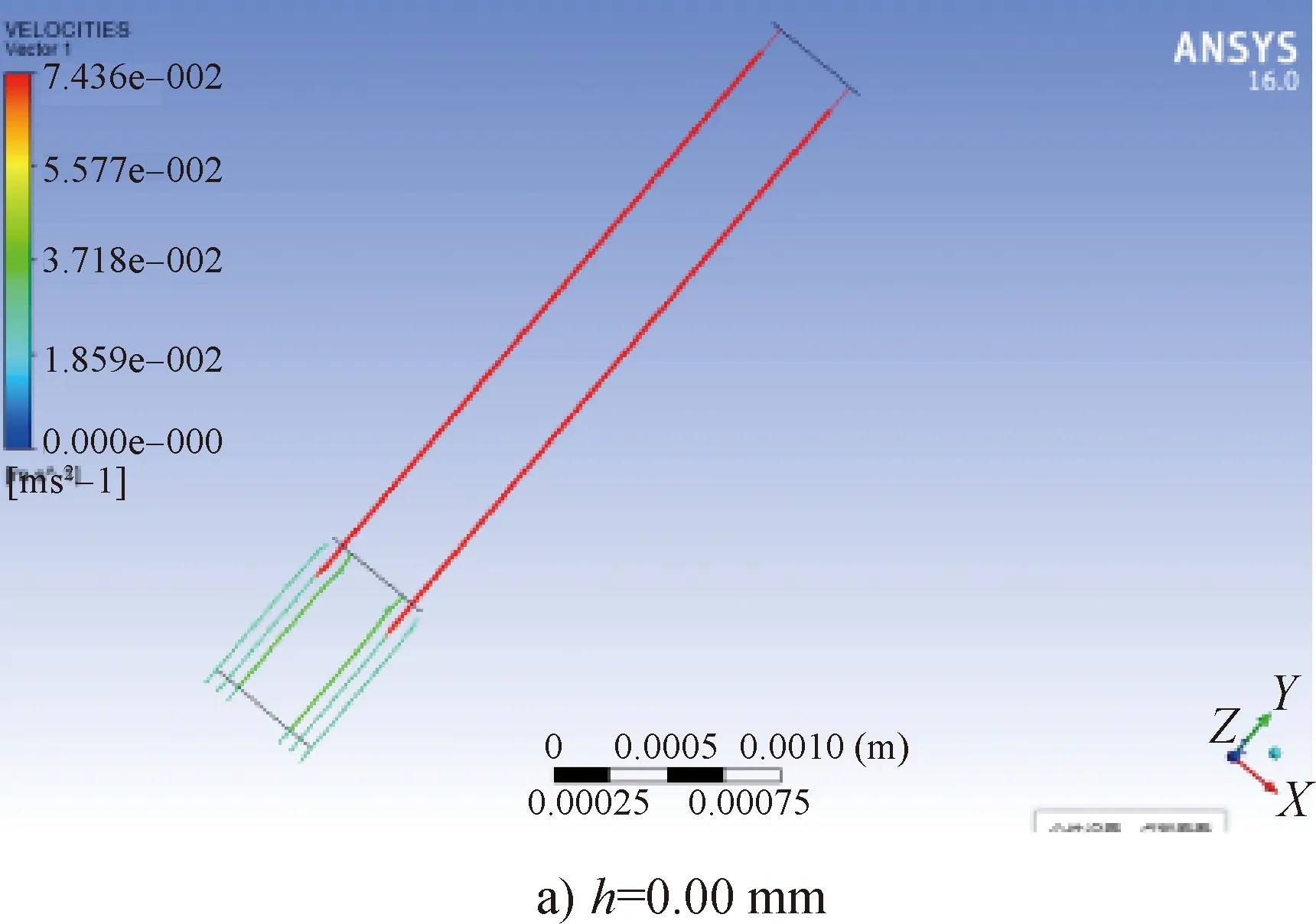
可以看出，熔体在微孔内的流速最大，且h=0.00 mm时的流速远大于h≠0.00 mm时的流速(最大值为0.074 3 m/s)。熔体在挤出段的速度(位于左下方)是法向流速和切向流速的叠加，从而使熔体发生胀大。熔体挤出微孔后便失去了纺丝组件壁面的束缚。

挤出熔体的轴向和径向的流速分布折线图分别如图6所示。其中，横轴零点处为熔体离开微孔时的出口面，折线图横轴数据表示熔体距出口面的距离。

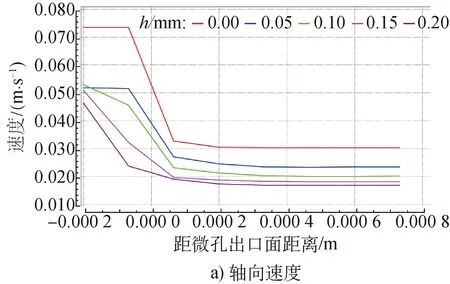
由图6 a)可知，在距出口面0.20 mm的范围内，熔体的流速变化趋势基本一致，与钢针缩进量无关，但熔体的流速随h的增大而减小。h为0.00和0.05 mm时，熔体在微孔流道内流速稳定，当熔体从微孔的圆环段流入圆形段后，其流速迅速减小。当h>0.05 mm时，熔体速度缓慢减小，速度稳定区消失。

由图6 b)可知，当h=0.00 mm，即微孔截面形状为单一圆环时，聚丙烯熔体在孔内的径向流速为0.000，说明微孔内的熔体不存在径向运动。熔体在接近微孔出口面时流速开始为负，说明熔体存在向外胀大的趋势，当熔体挤出微孔后，其径向流速逐渐增大然后减小为0.000。

当h≠0.00 mm时，熔体从环形微孔段进入圆形段微孔后，其径向流速迅速加快，说明熔体向微孔中心的胀大反应加快。当熔体接近出口面时，其径向流速又快速回落为0.000，说明在接近出口面时，熔体的胀大反应结束。当熔体挤出微孔后，其径向流速向坐标负方向迅速增加，然后又逐渐减小。由动量方程可知，熔体在挤出微孔后的流速由切向速度和法向速度组成。因熔体在微孔内流动时其内部分子链发生了较明显的取向，但在挤出后失去微孔壁面的约束，分子链又发生解取向，导致熔体发生回弹，所以，在离开出口面的一段时间后，熔体的径向流速先向负方向快速增加，然后回落，径向流动趋于停止。之后，熔体的流动主要表现为轴向流动，纤维的直径将不再发生变化。

2.2 钢针缩进量对熔体挤出胀大比的影响

熔体挤出胀大比为挤出丝条的最大截面积与喷丝微孔截面积之比。钢针缩进量h不同时，熔体离开微孔出口面后的半径变化和挤出胀大比折线图分别如图7和图8所示。

图7 熔体挤出段半径变化图

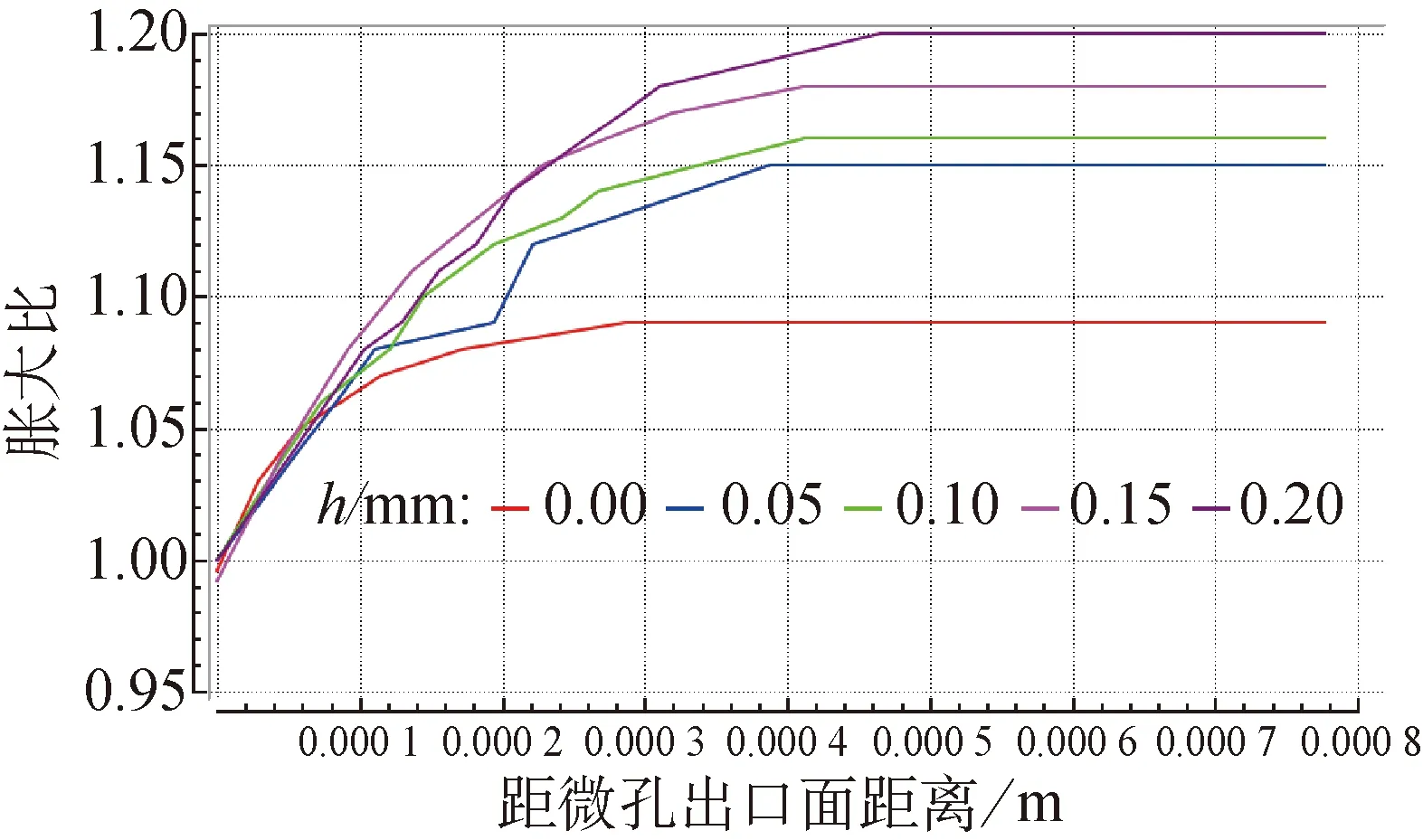
图8 熔体挤出胀大比变化折线图

从图7可发现，钢针缩进量对熔体的挤出胀大比无明显影响。当h=0.00 mm时，纤维直径约为0.56 mm，h≠0.00 mm时，纤维直径约为0.60 mm，二者差别不明显。由图8可知，熔体的挤出胀大比随h的增大从1.05增至1.20。根据挤出胀大原理分析得，h=0.00时，环形微孔内熔体的松弛时间较长，自身应力在与微孔壁面接触时得以释放，其回弹形变能减小，故挤出后的胀大反应较小，h=0.05 mm时次之。总体而言，聚丙烯熔体在微孔中的挤出胀大比处于合适的范围(1.00～1.35)内[15]。

2.3 钢针缩进量对中空度的影响

钢针缩进量不同，挤出微孔后熔体中空部分的起点不同，由其截面变化图(图9)可知，随着h的增加，微孔内熔体的胀大现象趋于明显，其中空直径逐渐减小。h=0.05 mm时微孔内熔体的空心直径为0.0125 cm，是h=0.20 mm时的6倍。当熔体离开微孔的出口面后纺制而成的初生中空纤维的空心直径随钢针缩进量的增加而逐渐减小。距微孔出口面的0.40 mm处，初生中空纤维的空心直径趋于稳定。h=0.00 mm时，初生中空纤维的空心直径胀大后基本能回复到刚离开微孔出口面时的半径值。与h=0.00时纺制的初生纤维相比，h=0.05 mm时初生中空纤维的空心直径有所回落，但在距出口面0.20 mm后，其空心直径出现反超，距出口面0.40 mm后，其空心直径超过钢针直径，达0.17 mm。

根据聚丙烯熔体离开微孔出口面后的截面变化(图7)和图9熔体挤出前后空心直径的变化，计算并绘制了中空度的变化曲线(图10)。由图10可知，钢针缩进量不同时，熔体或初生中空纤维的中空度变化趋势与熔体离开微孔出口面前后的截面变化趋势相同。随着h的增加，环形微孔通道内聚丙烯熔体的中空度从37%逐渐降低。聚丙烯熔体挤出成为初生中空纤维后，其中空度开始变大。通过对比h=0.00 mm和h=0.05 mm时中空度的变化发现：环形微孔流道内熔体的中空度受h的影响，h越大，熔体的中空度越小；熔体离开喷丝微孔成为初生中空纤维后，h=0.05 mm微孔内制备的初生中空纤维的中空度开始快速增大，最后大于h=0.00 mm时纺制的初生中空纤维的中空度。这是由于熔体从h=0.05 mm的微孔中挤出后仅失去了孔壁面的束缚，开始胀大，其中空度增大，而从h=0.00 mm的微孔内挤出后，熔体同时失去孔壁和钢针内外两个壁面的束缚，其胀大反应在这两个方向相互抵消，故挤出后熔体的中空度变化并不明显。

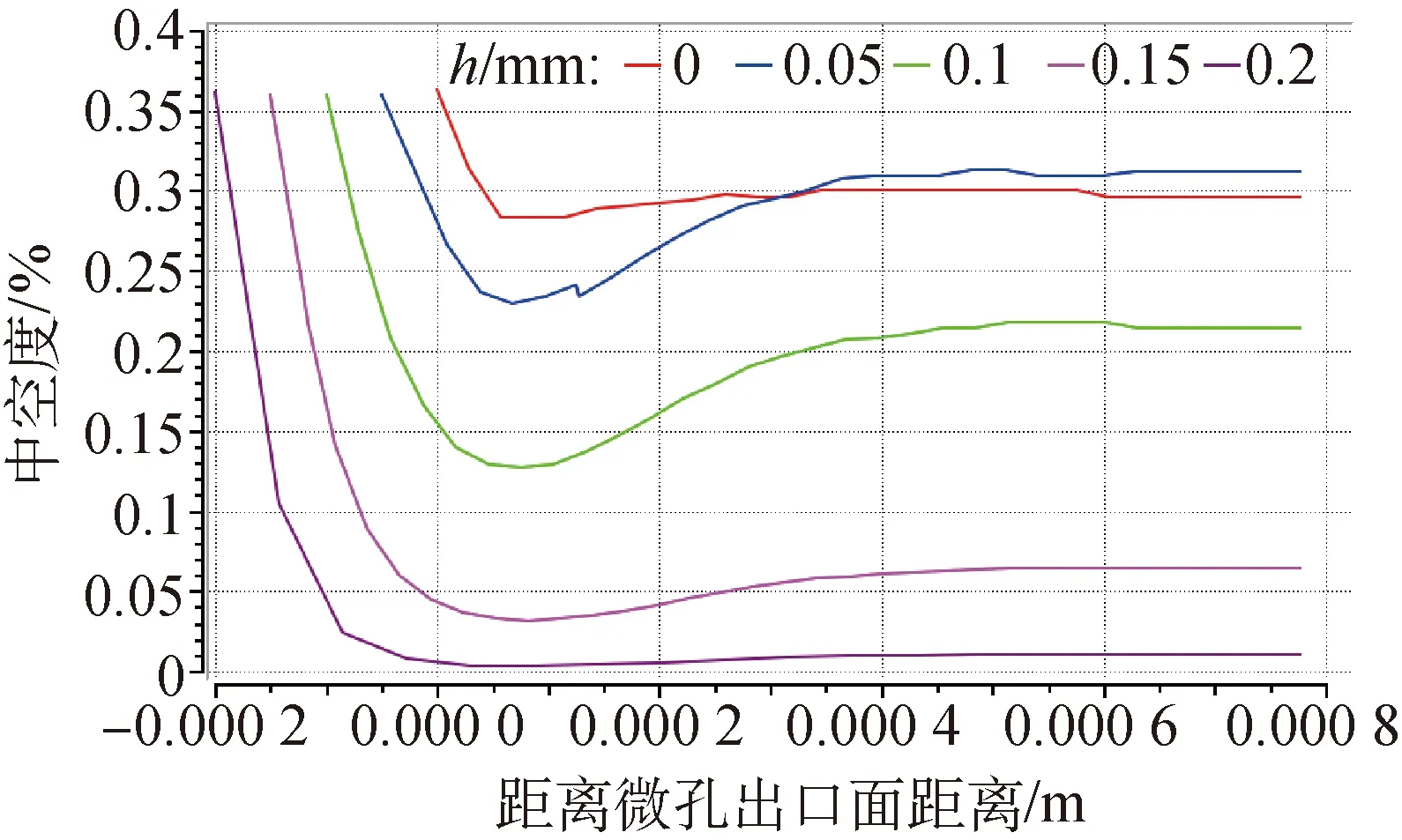
图10 中空度的变化折线图

通过数值模拟，分析在圆形微孔内同轴圆形钢针的进缩量不同时所纺制的中空纤维的中空度变化(图11)。结果表明：当h=0.05 mm时，可制备中空度最大(32%)的中空纤维；当h>0.20 mm时，中空纤维的中空度最小(2%)。

图11 中空纤维的中空度随h变化的折线图

3 数值模拟结果验证

设计加工圆弧狭缝式喷丝板，在钢针缩进量h分别为0.00、0.05、0.10、0.15和0.20 mm的喷丝板中纺制中空纤维，观察各中空纤维试样的截面形状，并与模拟计算结果进行对比(图12)，验证本文数值模拟方法的合理性和可靠性。

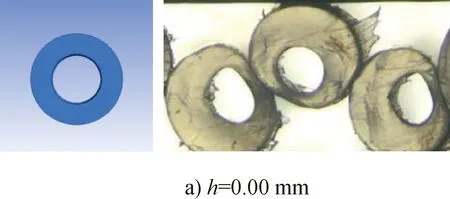
从图12可以看出，试验纺制的各中空纤维的截面形状不尽相同，这是由于纺丝组件内部的熔体压力、熔体流速和温度不均匀导致。对比模拟计算结果发现，试验所得到中空纤维的截面形状与模拟结果基本吻合，说明本文所建立的模拟方法具有一定的合理性和可靠性。

4 结论

(1)聚丙烯熔体在微孔内部具有最大流速，且h=0.00 mm时的流速远大于h≠0.00 mm时的流速。聚丙烯熔体的流速随h的增大而减小。当熔体从微孔的圆环段流入圆形段后，其流速迅速减小。

(2)钢针缩进量不同时，熔体或初生中空纤维的中空度变化趋势与熔体离开微孔出口面前后的截面变化趋势相同。中空纤维的中空度在钢针进缩量为0.05 mm时可达最大，为37%，之后随h的增大而减小。h=0.20 mm时，中空纤维的中空度基本消失，说明钢针缩进量在0.00～0.20 mm时，可采用圆形微孔内置同轴圆形钢针的微孔结构成功纺制中空度不同的中空纤维。