非关联流动准则条件下条形锚板抗拔特性上限分析

2021-10-18蒋志琳王崇淦谢春玲

铁道科学与工程学报 2021年7期

蒋志琳，王崇淦，谢春玲

(湖南中大设计院有限公司，湖南长沙410075)

锚板作为一种高效、简单且成本低廉的能提供抗拔力的基础型式，在工程中得到了广泛应用，其抗拔承载特性也一直是岩土工程研究的重点。基于其破坏范围和破坏机理，锚板可分为浅埋锚板和深埋锚板[1−2]。浅埋锚板破坏时上覆土体存在明显的破坏面，且从锚板端点向上延伸到地表，呈整体剪切破坏。而深埋锚板则是以锚板周围土体的局部破坏为主，土体中没有明显的破裂面，一般伴随着地表隆起现象。对于浅埋锚板的抗拔承载特性研究，主要有以下几种研究方法：模型试验、极限分析法、极限平衡法和数值分析方法。由于极限分析方法避免了复杂的应力−应变过程，相较于极限平衡法具有严格的理论基础。因此，极限分析方法成为岩土工程问题研究的最常见且有效的方法之一，在浅埋锚板抗拔特性的研究中也非常有效。因而，对于锚板抗拔承载特性取得了卓有成效的研究。基于极限分析上限定理，黄茂松等[3−4]基于刚性块体破坏机制，探究了浅埋条形锚板的抗拔承载特性。赵炼恒等[5−6]考虑岩土体材料固有的强度非线性特性，采用外切线方法引入非线性强度指标，开展了锚板抗拔特性分析。考虑到外切线方法引入的强度指标是相同的，塑性应变增量方向是一致的，并没有反映岩土体摩擦角随正应力的变化关系。因此，并非真正意义上的非线性特性分析。在极限分析上限定理的基础上，基于非线性破坏准则和关联流动法则，王洪涛等[7-8]构建了条形锚板的曲线型破坏机制，通过虚功率原理建立了抗拔力的泛函，根据变分原理得到了条形锚板的极限抗拔力。进一步，ZHAO等[9−10]构建了圆形锚板的抗拔破坏机制，开展了圆形锚板的抗拔特性分析。在锚板剪胀特性的研究方面，MERIFIED等[11]采用极限分析有限元方法研究了砂土中水平和竖直条形锚板的极限抗拔力，深入分析了土体内摩擦角、剪胀角、锚板埋深和粗糙度等因素的影响。GIAMPA等[12]考虑砂土的剪胀效应，采用模型试验、极限平衡方法、以及数值分析方法研究了浅埋圆形螺旋锚的极限抗拔力。但均基于线性准则，并没有考虑岩土体材料固有的非线性特性。然而，已有研究大多建立在岩土体材料服从相关联流动法则的基础上。大量研究成果也证实：岩土体材料一般并不遵循相关联流动法则[13−16]，岩土材料的膨胀角与摩擦角往往是不一致，极限状态产生的剪胀角一般小于相关联流动准则要求的值(即，内摩擦角)，岩土材料服从非相关流动规律[17−19]，采用相关联流动法则往往会高估土体的剪胀特性，当材料的剪胀角不等于摩擦角时，材料服从非关联流动法则。因此，SHI等[20]基于非线性Mohr-Coulomb准则以及非关联流动法则，分析了浅埋条形锚板的抗拔特性，其结果表明，土体的强度非线性和剪胀特性对锚板的极限抗拔力存在明显影响。赵炼恒等[5]考虑非关联流动法则和非线性Mohr-Coulomb准则，探究了水平浅埋矩形锚板的极限抗拔力。此外，考虑非关联流动法则和非线性破坏准则对岩土结构的稳定性或承载力的影响，也取得了较为丰富的成果[21−24]。但上述方法均通过“外切线”方法引入非线性强度指标，使得塑性应变增量方向一致，忽略了强度指标随正应力的变化关系，并非真正意义上的非线性分析。鉴于同时考虑岩土体材料强度非线性和剪胀特性对锚板抗拔特性的研究尚未见报道，本文基于非线性Mohr-Coulmb破坏准则和非关联流动法则，通过对非线性准则进行修正从而考虑土体的剪胀特性，在机动许可的速度场中计算内能耗散功率和外力功率。通过虚功率原理建立抗拔力的泛函表达式，采用欧拉方程和Runge-Kutta法得到破裂面方程，从而得到条形锚板的极限抗拔力。通过与有限元数值分析结果进行对比说明了本文方法的有效性，进一步开展了土体的剪胀特性和非线性特性对条形锚板的抗拔特性分析。本文研究综合考虑了土体的强度非线性和剪胀特性对锚板抗拔性能的影响，具有一定的理论研究价值和实际工程意义。

1 基本理论

非线性是岩土体材料非常重要的特性，主要表现在土体参数摩擦角会随着应力水平的变化而变化。在σ-τ平面内，它表征的是正应力与剪切强度的非线性关系[9−10,25]，如图1所示。当一个应力矢量从原点逐渐增加到该屈服曲线时，土体便达到屈服，并开始发生破坏。若将塑性正应变速率和剪切应变速率组成的坐标系与应力坐标系重合，当土体服从相关流动法则时，屈服点处的总塑性应变速率和屈服面正交，且总塑性应变速率与塑性剪切应变速率之间的夹角为φt，因此，φt=atan(dτ/dσ)。

图1 非线性Mohr-Coulomb准则Fig.1 Nonlinear Mohr-Coulomb failure criterion

对于非线性Mohr-Coulomb破坏准则[5-7,9,26]，其表达式为：

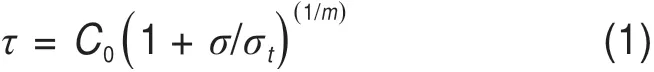
其中，C0为土体的初始黏聚力;σt为土体的单轴抗拉强度，在σ-τ平面内，其分别表示屈服准则与纵轴、横轴的截距;m为表征土体强度非线性的系数，m≥1.0,当m=1.0时则退化为线性Mohr-Coulomb准则。

然而根据极限分析上限理论，岩土材料在发生塑性流动时服从相关联流动法则，此意味着产生较大的剪胀，实际上岩土材料的剪胀并没有预测的那么大。大量研究成果也证实：岩土体材料一般并不遵循相关联流动法则[13−16]，当材料的剪胀角不等于摩擦角时，材料服从非关联流动法则，此时速度方向与间断面的夹角为剪胀角。而岩土体材料都具有强度非线性特性，为能使用极限分析定理，考虑非关联流动准则，采用非线性剪胀系数η直接对破坏准则进行修正[23−24]，修正后的非线性Mohr-Coulomb破坏准则为：

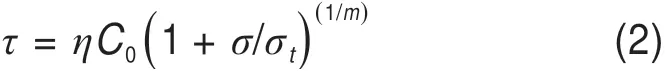
2 上限分析

2.1 模型建立

本文假定地表水平，锚板水平埋设，且锚板埋深属于浅埋范围，即锚板上覆土体破裂时存在明显的破裂面。土体服从非线性Mohr-Coulomb准则和非关联流动准则，锚板在承受上拔荷载时，锚板和土体视为整体向上运动，破坏面上速度与破坏面切线的夹角为剪胀角ψ，破坏面切线与水平方向的夹角为θ，由图2可知，cotθ=g′(z)。土体破裂面曲线方程假设为y=g(z)，锚板埋深为H，锚板宽度为B=2r，地表破坏点至锚板中点的水平距离为L，锚板承受的上拔力为Pu，地表超载为σs。以z为自变量。

图2 水平浅埋锚板抗拔破坏机制Fig.2 Uplift failure mechanism of shallow horizontal anchor plate

2.2 功率计算

取z方向单位长度微元体分析，由图2中几何关系可知，破坏面上的长度

非线性准则和非关联流动法则条件下，单位面积上的内能耗散功率为[26]

因此，破坏面上内能耗散功率为

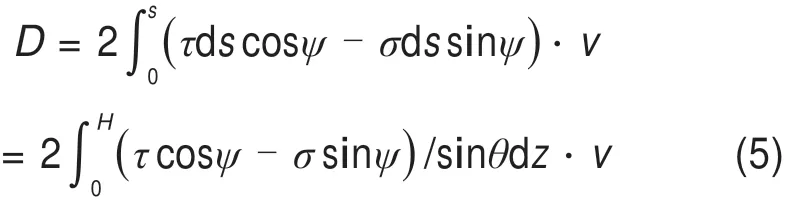
重力功率

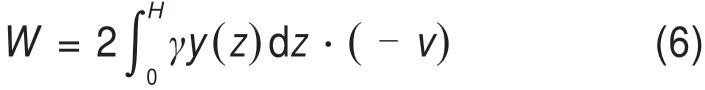
上拔力功率

地表超载功率

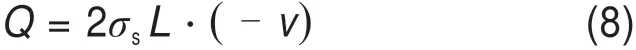
根据虚功率原理建立平衡方程得：

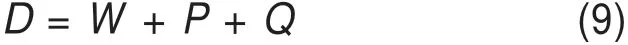
由此，可得条形锚板的极限抗拔力为

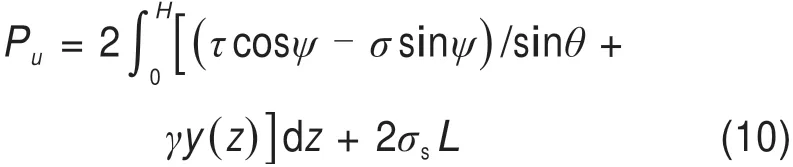
2.3 最小上限解条件

根据ZHANG等[26]的研究，在临界状态下，当功率平衡和静力平衡条件同时满足时可得到最小的上限解答。由图2所示的轴对称破坏机制可知，在水平方向上合力为0，且锚板上覆土体视为刚塑性体整体向上平移。在竖直方向上，合力为

在任意一组虚位移中，都满足虚功率平衡原理，因此

显然，在任意一组容许的虚位移中，竖直方向上满足力的平衡条件。由此

式中：

2.4 欧拉方程

抗拔力表达式(13)为典型的包含多个函数的积分型泛函，根据变分极值原理，抗拔力取极值时的极值曲线必然满足如下欧拉方程。

其中

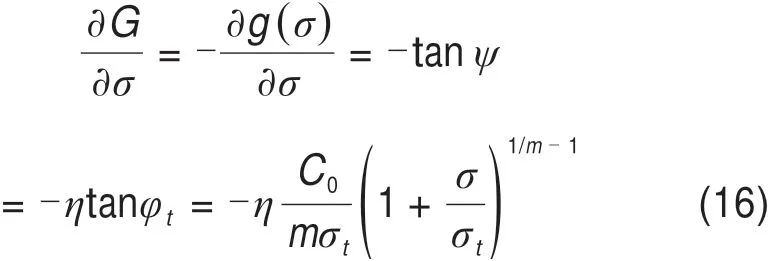
将式14(a)代入式(15)可得

化简可得

2.5 变分横截条件

此外，由于浅埋锚板的破裂面由锚板端点向上逐渐延伸到地表，破坏面(即极值曲线)一端固定，另一端在直线z=H上移动，δy=0，δz是任意的。根据可动边界条件的泛函极值原理，抗拔力泛函取极值时除满足充要条件—欧拉方程—之外，还必须满足必要条件—变分横截条件，如下

因此，在地表处，有边界条件为

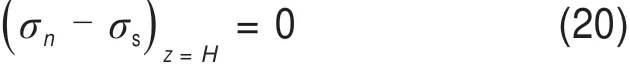
由式(20)可知，在地表处，土体破裂面上正应力等于地表超载。

此外，根据图2所示的破坏机制可知位移边界条件如下

于是，式(18)中的偏微分方程组可根据Rung-Kutta方法结合式(20)和式(21)中的边界条件进行求解。

3 对比分析

为验证本文方法的有效性与准确性，采用极限分析有限元方法对本文计算结果进行对比。有限元模型如图3所示，由于水平锚板在地表水平时其抗拔破坏机制为轴对称机制，故取模型的1/2进行建模。为保证锚板在上拔过程中无水平横向位移，对锚板中点施加约束，锚板采用板单元，中点处施加集中荷载。此外，模型边界条件为：模型上部边界为地表，无约束；左右两侧边界施加法向约束；底部边界固定约束。

图3 抗拔锚板有限元模型Fig.3 Finite element uplift model of anchor plate

当非线性系数m=1.0时，非线性Mohr-Cou‐lomb破坏准则将退化为线性Mohr-Coulomb准则。此时，考虑剪胀特性的非关联流动法则对强度准则的折减为[16]

其中

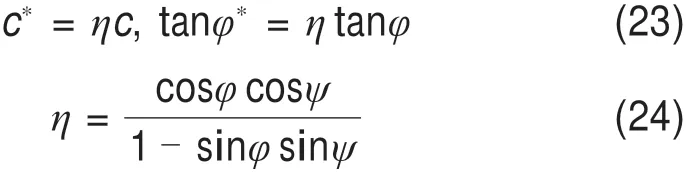
式中：c，φ分别表示初始的土体黏聚力和内摩擦角；c*，φ*分别表示折减后的土体黏聚力和内摩擦角；ψ为剪胀角。

当假定土体材料服从相关联流动法则时，土体的剪胀角等于摩擦角，而当土体服从非相关联流动法则时，土体的剪胀角小于摩擦角。在线性准则条件下，将屈服准则进行强度参数的折减来考虑非相关联流动法则的影响。因此，本文采用极限分析有限元方法分别分析以下3种工况：1)材料服从相关联流动法则；2)材料服从非相关联流动法则；3)考虑非相关流动法则影响，对强度准则进行折减的相关联流动法则，即采用式(23)的折减后强度参数且服从相关联流动法则。将上述工况计算结果与本文方法计算结果进行对比，如图4所示。

图4 极限抗拔力对比分析Fig.4 Comparison of ultimate pullout capacity

在线性准则条件下，考虑关联和非关联流动法则的影响，采用极限分析有限元方法对本文结算结果进行了案例对比分析，如图4所示。当土体服从关联流动法则时，极限分析有限元结果(数值解)稍大于本文计算结果(理论解)，在埋深较小时，两者相对误差较大，随着锚板埋深的增加，两者相对误差逐渐减小。在非关联流动法则条件下，本文理论计算结果与采用折减后的强度准则数值计算结果(即工况c)吻合较好，两者结果均大于非关联流动准则条件下的有限元分析结果(即工况b)。总体上看，本文理论结果与数值计算结果吻合较好，可以说明本文方法的有效性和准确性。

4 参数分析

在非线性Mohr-Coulomb准则条件下，考虑岩土体材料的剪胀特性，得到了浅埋条形锚板的极限抗拔力。研究表明，锚板的极限抗拔力受众多因素的影响，尤其是在非线性准则条件下[7−10]。基于此，对考虑剪胀特性的岩土体材料中的条形锚板的极限抗拔力进行了参数的影响分析，如图5所示。并采用无量纲抗拔因子Npu表征条形锚板的极限抗拔力Pu，且Npu=Pu/γBH。

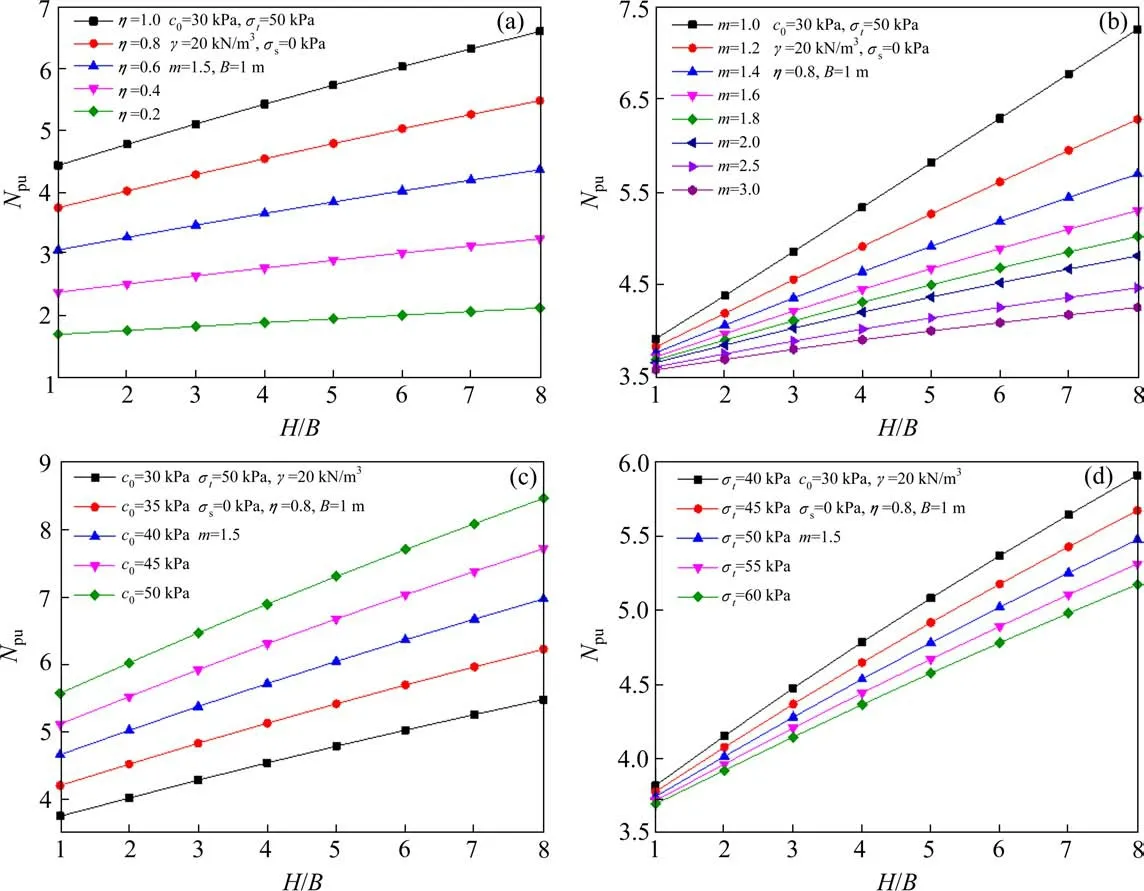
图5 条形锚板极限抗拔力参数影响分析Fig.5 Analysis of the effect of parameters on the ultimate pullout capacity of strip anchor plate

由图5可知，随着锚板相对埋深率的增大，抗拔因子逐渐增大。在非线性Mohr-Coulomb准则条件下，条形锚板的无量纲抗拔因子随非线性剪胀系数的增大逐渐较小。非线性剪胀系数越大，锚板相对埋深率对抗拔因子的影响越显著，如图5(a)所示。条形锚板的抗拔因子随非线性系数的增大逐渐减小，且趋势趋于平缓，非线性系数越小，抗拔因子随锚板相对埋深率的变化越显著，如图5(b)所示。抗拔因子随初始黏聚力的增大而增大，随土体抗拔强度的增大而减小，且当抗拉强度较大时，锚板抗拔因子随相对埋深率的影响越显著。

对于浅埋锚板，上拔破坏时土体存在明显的破裂面。在锚板工程设计中，锚板的极限抗拔力是其抗拔特性的重点，但上覆土体的破坏范围也是值得注意的。因此，同时考虑土体强度非线性和剪胀特性，对浅埋条形锚板上覆土体破裂面形状进行了参数影响分析，如图6所示。其中，锚板宽度B=1.0 m，上覆土体重度γ=20 kN/m3，锚板埋深H=6.0 m，地表超载σs=0 kPa，其余参数详见表1。

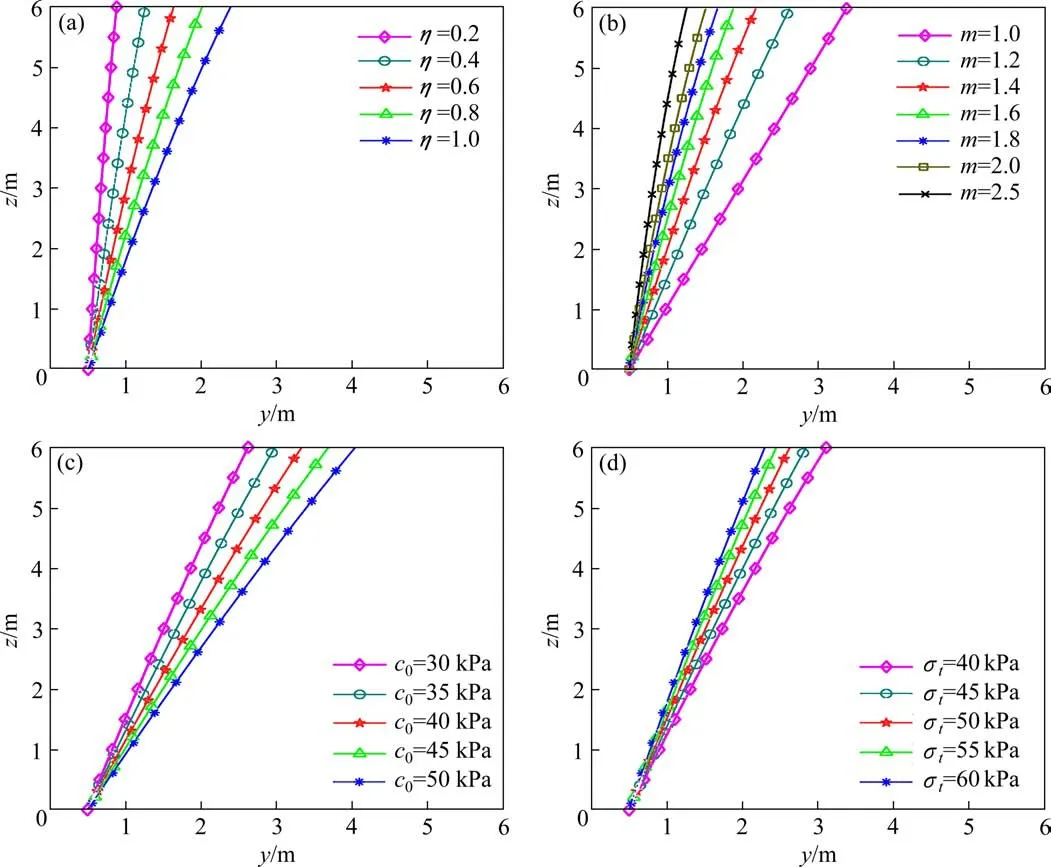
图6 参数对土体破裂面形状的影响分析Fig.6 Analysis of effect of parameters on the shape of soil fracture surface

表1 参数取值Table 1 Values of parameters

由图6可知，考虑剪胀效应的非线性剪胀系数η，非线性系数m，土体初始黏聚力和抗拉强度对锚板上覆土体的破坏范围均存在较为显著的影响。在非线性准则条件下，随着非线性剪胀系数η的增大，地表破坏宽度逐渐增大，如图6(a)所示。随着非线性系数m的增大，土体破裂面由直线逐渐变化为曲线，破坏范围逐渐减小，且只在线性准则条件下破裂面呈直线，在非线性条件下破裂面呈曲线，如图6(b)所示。当土体初始黏聚力增大、或土体抗拉强度减小时，其地表破坏宽度逐渐增大。在线性准则条件下，土体初始黏聚力增大、或土体抗拉强度减小均表现为土体强度参数的增大，因此，土体破坏范围增大。