基于MEC-BP神经网络的基坑水平位移反演分析
2021-10-18李步遥司马军
李步遥,司马军,2
(1.武汉大学 土木建筑工程学院,湖北 武汉430072;2.岩土与结构工程安全湖北省重点试验室,湖北 武汉430072)
近年来,随着城市轨道交通建设的快速发展,地铁车站开挖深度越来越大,对基坑变形的设计要求也越来越高。由于岩土材料性质的复杂性和敏感性、取样的扰动性以及施工条件的不确定性,岩土参数的室内试验结果与现场实际情况往往有较大差别[1],基坑工程岩土设计参数的选择面临着极大挑战。为了降低工程风险同时避免投资浪费,许多学者根据现场监测结果展开了岩土参数反演分析研究[1−2]。为了克服传统优化算法的不足,神经 网 络 法[3−4]、遗 传 算 法(GA)[4−6]、粒 子 群 算 法[7]、进化差分算法[8]等人工智能方法在反分析问题中得到了大量应用。其中,BP神经网络具有学习能力强、可塑性好等优点,但传统BP神经网络易陷入局部最优;主要原因是BP神经网络初始权值和阈值的选择具有随机性,影响了模型性能。思维进化算法(Mind Evolutionary Computation,MEC)[9]借鉴了遗传算法中群体和进化的思路,引入了反映人类思维特点的趋同与异化过程,改进了传统进化算法早熟、收敛速度慢等缺点,具有极强的全局寻优能力。一些学者利用MEC定向搜索最优初始权值和阈值来优化BP神经网络性能,建立MEC-BP神经网络[10],应用于岩土渗透系数反演[11]、桩身轴力预测[12]等问题,取得了较好的效果。然而,目前鲜有学者将MEC-BP神经网络方法应用于基坑工程。鉴此,本文将MEC-BP神经网络运用到深基坑工程反分析问题中,提出根据实测水平位移反演土层参数的方法,并采用文献算例进行了验证;同时,将该方法与常规BP神经网络、遗传神经网络(GA-BP)和修正高斯−牛顿法(G-N)[13]等作了对比,分析了不同适应度函数对反演结果的影响。
1 基于MEC-BP神经网络的基坑位移反演分析方法
1.1 BP神经网络
BP神经网络为一种多层前馈神经网络,主要特征为输入信号前向传递,误差逆向传播。神经网络的误差为内部链接权重的函数。网络的训练过程就是通过误差函数的梯度下降,迭代地改进权值和阈值,使网络实际输出值不断逼近期望输出。但其初始权值和阈值具有随机性,使得BP神经网络常出现收敛速度慢、易陷入局部最优、有时迭代过程中目标函数发生震荡等缺陷。
1.2 思维进化算法(MEC)
思维进化算法(MEC)的详细介绍见文献[9,11],其基本思路为:第1步,在解空间内诞生一定数量的初始种群群体,根据得分函数,对种群个体依次进行打分并筛选出初始种群中得分最高的若干个体。第2步,以上述得分最高的个体为中心,在其周围再生成一些新的个体,这些个体的集合定义为优胜子种群和临时子种群。第3步,在各子种群内部进行趋同操作。利用种群成熟判别函数确认子种群是否成熟。成熟的子种群结束趋同操作,并以最优个体的得分作为群体得分;不成熟的子种群将以新的中心产生子群体,再进行多次趋同操作直至成熟。第4步,在全局范围内进行异化操作。如果存在临时子种群的得分高于优胜子种群的得分,则进行异化操作,用得分高的临时子种群中的个体去替代得分低的优胜子种群内的个体,从而释放被取代的优胜子种群内部的个体,这些个体在全局空间内重新组成新的临时子种群。
1.3 MEC-BP神经网络及其位移反演分析步骤
MEC-BP神经网络是根据选定的BP神经网络拓扑结构,设置思维进化算法初始参数,利用思维进化算法搜索出全局最优个体,通过解码得到最优的初始权值和阈值;然后将优化后的初始权值和阈值代入BP神经网络,再利用训练样本对神经网络进行学习,最终提高BP神经网络的收敛速度和拟合精度。
本文提出基于MEC-BP神经网络的基坑位移反演分析流程如图1所示,具体步骤如下:

图1 MEC算法优化BP神经网络流程Fig.1 Process of BP neural network optimized by MEC algorithm
1)建立有限元模型,并确定待反演土层参数及取值范围。
2)生成训练样本。将步骤1选取的待反演土层参数采用正交试验设计方法确定试验方案,生成目标样本T,由T代入有限元模型正演分析得位移样本P,将样本P和T分别作为网络的训练输入和输出样本,并对训练数据进行归一化预处理。
3)根据步骤2得到的训练样本,选择BP神经网络的拓扑结构,包括网络输入层、输出层、隐含层神经元个数和网络参数设置。
4)设置MEC算法参数,包括迭代次数、初始种群、优胜子种群和临时子种群个数,根据确定的网络拓扑结构,选择网络权值和阈值编码长度。
5)将待优化的权值和阈值根据步骤4设置的参数进行实数编码,并产生随机的初始种群、优胜子种群和临时子种群。
6)根据训练样本计算各种群和个体得分,种群个体得分为输出样本与目标样本间适应度函数的倒数。研究表明,采用不同适应度函数时网络训练效果存在差异。作为对比,下文采用了2种适应度函数,即均方差函数MSE[14]和标量误差函数Ferr[15],详见后面2.3节分析。公式如下:
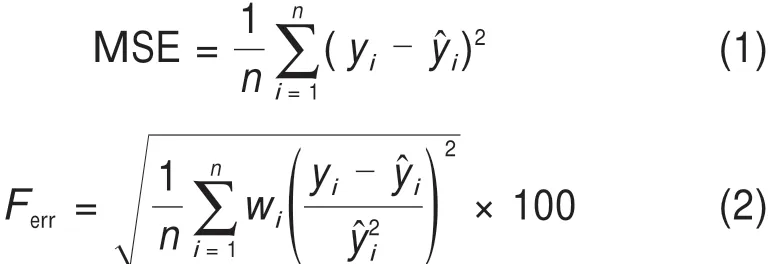
式中:n为训练样本总数;yi为第i个输出值;ŷi为第i个目标值;wi为第i点对应的权重,本文取1.0。
7)对各个子种群执行趋同和异化操作,通过不断迭代,将当前的得分与历史最优得分比较,更新优胜种群及其最优得分。
8)输出最优个体。判断每次得到的最优个体分数是否发生变化或是否已达到最大迭代次数,若满足精度,输出最优个体,优化过程终止,否则重复步骤6和步骤7。
9)训练网络。将步骤8获得的最优个体进行解码并将优化得到的初始权值和初始阈值赋值给BP网络,利用训练样本对BP网络进行学习。
10)仿真预测和评价。将测试样本即现场位移监测数据输入训练好的BP网络,得到待反演参数值,通过有限元正演分析得到预测的位移数据,并与监测位移数据进行对比,评价预测效果,反演预测效果的评价指标可采用水平位移绝对误差和函数SAE,其计算公式如下:
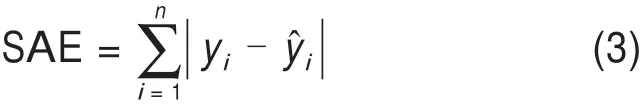
式中:n为输入位移样本总数;yi为预测位移样本;ŷi为监测位移样本。
2 算例
2.1 工程概况
选取文献[13]报道的美国芝加哥SQBRC基坑反演算例进行分析。该基坑开挖深度约为13.1 m,从上到下土层依次是填土、砂土、软黏土、硬黏土和坚硬黏土层。该基坑采用板桩加2层预应力锚杆和一层内支撑的支护形式,分4层开挖,分别对应4种工况,如图2所示。根据基坑SAA-1测斜管的桩身水平位移观测数据,可对不同工况的土层力学参数进行反演分析。据分析,软黏土层和硬黏土层的性质对基坑变形的影响最大,以下主要根据该2层土范围内的桩身水平位移进行反演分析[13]。
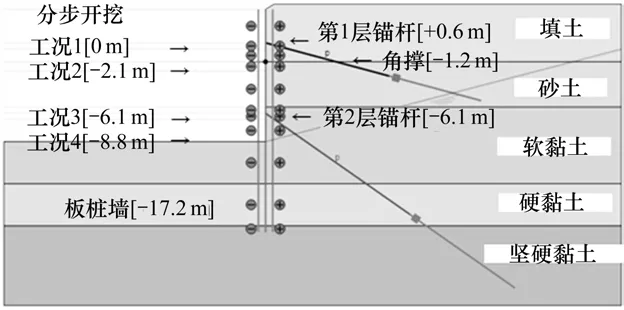
图2 基坑剖面图[13]Fig.2 Profile for deep excavation[13]
2.2 建立MEC-BP神经网络
为与文献[13]所采用的反演结果进行对比,本文建立的有限元模型、研究的目标土层和采用的土层反演参数及取值范围等内容与文献[13]保持一致。
2.2.1 土层反演参数及取值范围
与文献[13]相同,土层计算参数如表1所示。其中,填土、砂土和坚硬黏土采用HS模型,软黏土和硬黏土采用HSS模型。选取敏感性较强的软黏土与硬黏土2层土的Eref50及γ0.7作为反演参数,划分参数水平等级如表2所示。利用4因素4水平正交表L16(44)建立16组数据作为目标样本T;再将16组数据采用有限元模型正演分析得桩身水平位移数据,并选取上述2层土厚度范围内(约12 m)的水平位移作为输入样本P。在网络训练前,需采用归一化法对样本T和P进行数据预处理。
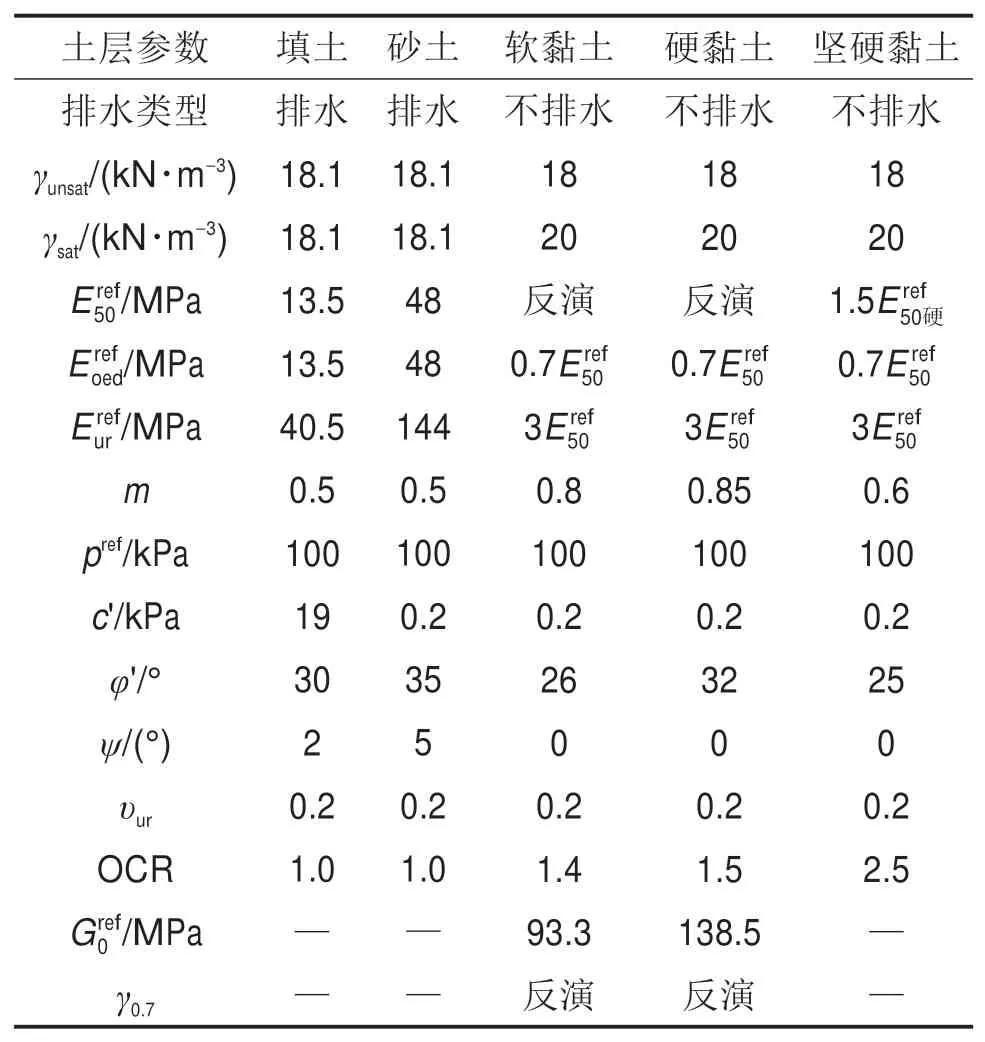
表1 有限元模型土层参数Table 1 Soil parameters for the FEM model

表2 土层参数水平等级划分Table 2 Level of classification for soil parameters
2.2.2 确定MEC-BP神经网络参数
BP神经网络采用3层拓扑结构,输入12个测点的基坑水平位移(测点间距1 m),即输入层节点数为12,输出4个反演参数即输出层节点数为4,而隐含层节点数采用高大启[16]提出的公式计算为8,故BP神经网络的拓扑结构为12-8-4。通过试算,BP神经网络最大训练步数设为3 000步,训练误差目标为10−6,隐含层、输出层的传递函数都选为logsig,训练函数选为贝叶斯正则化算法;MEC算法参数为:初始种群个数为700,优胜子种群和临时子种群个数分别为20和5,迭代次数为10。
2.2.3 参数反演方法
由于工况1开挖深度浅,桩身侧移较小,位移变化对土层参数不敏感,故本文只对工况2,工况3和工况4进行参数反演分析。首先,按照上一节介绍的方法对工况2~工况4分别建立MEC-BP神经网络。接下来,根据各工况的水平位移监测数据得到土层参数反演值。然后,将其反归一化后带入有限元模型得到各工况的水平位移计算值,并与监测数据进行对比。最后,采用水平位移绝对误差和函数(SAE)对反演结果进行评价,并与常规BP法、GA-BP法以及文献推荐的修正高斯-牛顿法(G-N)等进行对比。其中,GA-BP法的种群数量和迭代次数与MEC-BP法一致,采用自适应交叉和变异算子[17],交叉率和变异率分别为0.95和0.08。
2.3 反演结果分析
2.3.1 基于工况2的反演结果
根据工况2的测斜数据,采用MEC-BP方法反演得到的工况2~工况4桩身水平位移计算值与实测值对比如图3所示。从图3可以看出,基于工况2,MEC-BP方法反演的工况2桩身变形计算值与监测值基本一致,工况3和工况4的计算值与监测值则相差较大。这与文献[13]结论是一致的,原因是工况2条件下目标土层产生的应变水平相对较低,不能充分反映土层性质。

图3 基于工况2测斜数据反演分析的变形Fig.3 Deformations based on inverse analyses of Level 2 movements
基于工况2的不同方法反演效果评价如表3所示。其中,SAE值越大,表明水平位移计算值与实测值差别越大,反演效果越差。由表3可知,MEC-BP方法得到的各个工况SAE值最小,合计值也最小。以MEC-BP法(适应度函数为Ferr)为例,工况2~工况4的SAE值分别为1.9,44.61和51.64 mm,合计值为98.18 mm,总体上优于修正G-N方法[13]、GA-BP方法和常规BP法。此外,本算例MEC-BP法每次迭代时间只需要10~20 s左右,而GA-BP法平均每次迭代时间超过5 min,说明MEC-BP方法具有较快的收敛速度。
2.3.2 基于工况3的反演结果
基于工况3的测斜数据,反演得到的各工况水平位移计算值与实测值对比如图4所示。由图4可知,基于工况3,MEC-BP方法反演的各工况桩身变形计算值与监测值均基本一致。
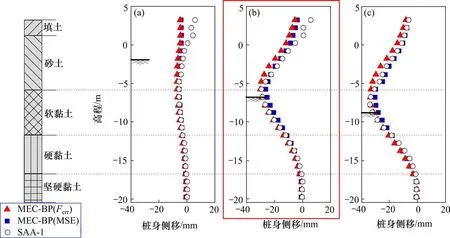
图4 基于工况3测斜数据反演分析的变形Fig.4 Deformations based on inverse analyses of Level 3 movements
基于工况3的不同方法反演效果评价如表4所示。由表4可知,MEC-BP法(适应度函数为Ferr)得到工况2~工况4的SAE值分别为6.82,12.93和21.59 mm,合计值为41.34 mm,总体上小于常规BP,GA-BP和修正G-N法的结果。另外,与表3相比,表4中工况2的SAE值增加4.97 mm,工况3与工况4的SAE值分别减少24.11 mm和19.76 mm,合计值减少38.90 mm。这说明基于工况3的反演结果明显优于基于工况2的反演结果。
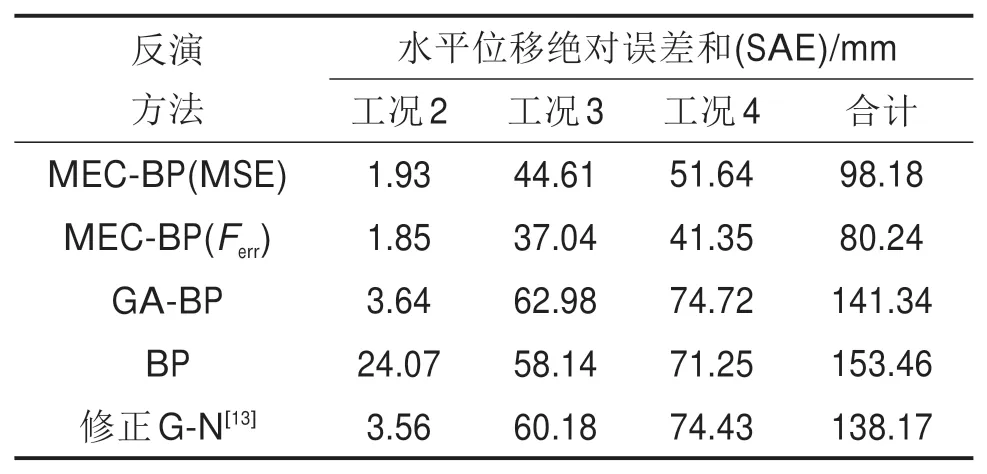
表3 基于工况2的不同方法反演效果评价Table 3 Error values of different inversion methods based on Level 2
2.3.3 基于工况4的反演结果
基于工况4的测斜数据,反演得到的各工况水平位移计算值与实测值对比如图5所示。由图5可知,MEC-BP方法反演的各工况桩身变形计算值与监测值也基本一致。
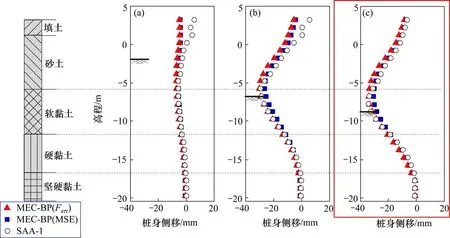
图5 基于工况4测斜数据反演分析的变形Fig.5 Deformations based on inverse analyses of Level 4 movements
基于工况4的不同方法反演效果评价如表5所示。由表5可知,MEC-BP方法(适应度函数为Ferr)得到工况2~工况3的SAE值分别为5.27,10.82和20.78 mm,合计值36.78 mm,总体上小于常规BP法、GA-BP法和修正G-N法的结果。另外,与表4相比,表5中工况2的SAE值减少1.55 mm,工况3与工况4的SAE值分别减少2.11 mm和0.81 mm,合计值减少4.47 mm。这说明基于工况4的反演结果略优于基于工况3的反演结果。

表4 基于工况3的不同方法反演效果评价Table 4 Error values of different inversion methods based on Level 3
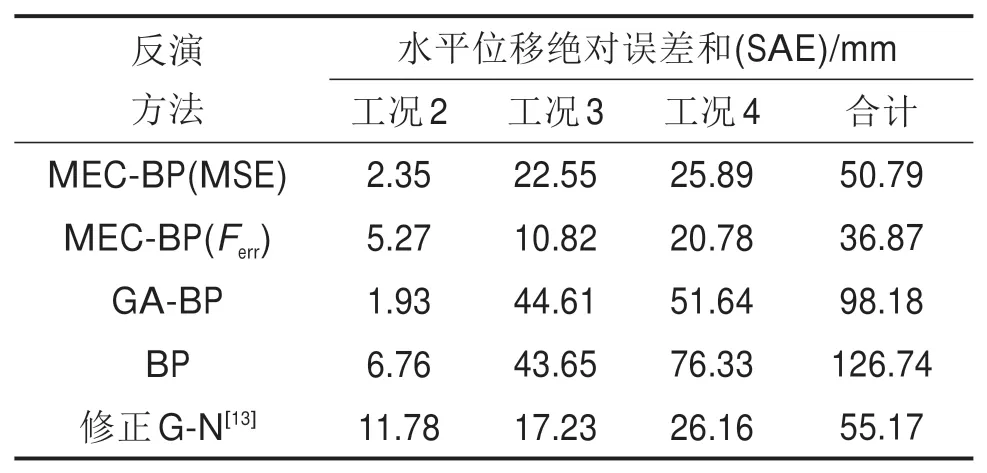
表5 基于工况4的不同方法反演效果评价Table 5 Error values of different inversion methods based on Level 4
2.3.4 适应度函数的影响
从图3~5可以看出,MEC适应度函数分别采用Ferr和MSE时,MEC-BP法反演的水平位移曲线总体上相似,但也存在一些差异。由表3~5可知,MEC-BP法(Ferr)反演得到的SAE合计值比MEC-BP法(MSE)分别少18.3%,40.6%和27.4%。可见,不同的适应度函数会对MEC-BP神经网络的反演结果产生影响,当MEC采用Ferr进行寻优时,可以提高基坑水平位移反演分析结果的稳定性和准确性。
2.3.5 土层参数优化结果
基于实测水平位移,采用MEC-BP法(Ferr)与修正G-N法[13]反演得到的土层参数结果对比如图6和图7所示。
从图6和图7可以看出,采用MEC-BP法(Ferr)反演得出的软黏土层Eref50值变化范围为7.5~14 MPa,随反演工况的增加有减小趋势;反演的硬黏土层Eref50值变化范围为20~55 MPa,随反演工况的增加有增大趋势。上述Eref50值反演结果和变化规律与文献[13]较为相似。MEC-BP法(Ferr)得出的2个黏土层的γ0.7值变化幅度较小,数值上与文献[13]有一些差异,但接近FINNO等[18]得到的1.0×10−4~2.0×10−4范围值。由此可知,MEC-BP方法的参数反演结果符合实际情况。
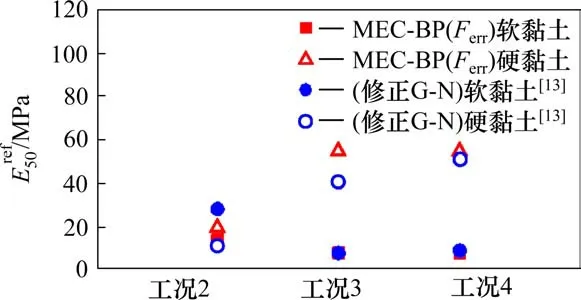
图7 SQBRC基坑土层参数γ0.7反演结果Fig.7 Optimized soil parameters for SQBRC excavation
3 结论
1)MEC-BP神经网络对多工况水平位移反演分析的结果与文献基本一致,验证了该方法的可行性和实用性。
2)MEC-BP方法的反演效果优于常规BP方法、遗传神经网络法(GA-BP)和修正高斯−牛顿法(GN),其收敛速度快于GA-BP神经网络。
3)采用标量误差函数Ferr进行寻优,可以提高MEC-BP水平位移反演分析结果的稳定性和准确性。
说明:本文仅将MEC-BP水平位移反演分析结果与文献算例结果进行了对比,所反演的土层参数较少。下一步还需结合更多工程实例,将MEC-BP方法应用于多源监测数据和多参数的反演分析研究,进一步提高岩土参数反演分析的实用性和准确性。
