地铁车站分项能耗原理模型及其简化研究*
2021-10-18清华大学苏子怡李晓锋
清华大学 苏子怡 李晓锋
0 引言
随着城市轨道交通系统的快速发展,地铁车站用电量不断增长。据统计,2019年我国城市轨道交通总用电量为152.6亿kW·h,同比增长15.5%,其中车站非牵引能耗占48%[1]。在车站非牵引能耗中,通风空调、照明、垂直交通系统能耗占比约80%[2]。因此,有必要研究地铁车站各用能主要项的合理能耗指标,对各系统的运行现状进行节能评估,探究节能运行管理措施的节能潜力。
为了研究地铁车站的合理能耗指标,需要建立地铁车站分项能耗模型。国内外已有诸多学者针对建筑用能水平和能耗指标进行了大量的研究,广泛采用的模型有基于统计回归和基于运行原理的模型。回归模型能够快速评估能耗,为了解建筑当前的用能水平提供参考[3-5]。但是回归模型缺乏实际的物理意义,无法针对不同类型、不同服务规模(客流、列车等)的车站制定合理的能耗指标,也无法分析能耗低或高的原因,对建筑系统节能运行改进的指导性不强。而原理模型则是基于对建筑物结构、通风、人员、运行等原理的分析,建立模型进行能耗模拟计算[6-7],其优点在于能够结合车站的实际情况,包括客流、列车、建筑等信息,给出车站的合理能耗指标,可以分析能耗高或低的原因,从而能够指导建筑的节能改造和运行。
因此,本文基于地铁车站各主要用能系统的运行特征,建立了详细的分项能耗原理模型,包括通风空调、照明和垂直交通系统。该模型可以通过输入车站的建筑和运营状况,对各分项用能系统的合理能耗进行详细计算。考虑到该原理模型需要的输入参数全面而复杂,现场调研和数据收集工作量大,为了满足实际工程应用的需要,通过敏感性分析得到了一组对模型计算结果有重要影响的输入参数。进而提出了简化的能耗模型,大大减少了模型的输入参数数量,降低了现场调研和数据收集的工作量,从而能够将能耗模型在全国不同气候区各城市地铁车站中进行大规模应用,快速计算车站的合理能耗,评估运行状况和节能潜力。
1 地铁车站通风空调系统能耗原理模型
通风空调系统是地铁车站第一大用能系统,其能耗原理模型由冷负荷模型和系统能效模型组成,参考相关文献和设计手册[8-10],结合地铁车站的特征建立模型。
(1)
式中EVAC为通风空调系统能耗,kW·h;QVAC为冷负荷,kW;EER为系统能效比;τVAC为通风空调系统运行时间,h。
1.1 冷负荷模型
地铁车站没有受到太阳辐射且土壤温度较稳定,因此外围护结构得热量相对稳定,围护结构蓄热对车站冷负荷的影响可以忽略[8],从而可以认为得热量近似等于冷负荷。地铁车站通风空调系统冷负荷由人员负荷、机械新风负荷、风机温升负荷、无组织渗风负荷、围护结构得热量、站内设备散热量组成。
1.1.1人员负荷
(2)
式中Qp为人员负荷,kW;qp为人员全热散热量,kW/人;Ain、Aout分别为车站进站和出站人数,人/h;ain、aout分别为乘客进站和出站时在站厅站台的停留时间,min。
1.1.2机械新风负荷
对于通风季,机械新风为车站供冷,车站冷负荷中不包括机械新风项。对于空调季,机械新风负荷计算公式为
(3)
式中Qm为机械新风负荷,kW;ρ为空气密度,kg/m3;Gm为机械新风量,m3/h;Δh为室外与站内空气的比焓差,kJ/kg。
1.1.3风机温升负荷
Qf=Pf
(4)
式中Qf为风机温升负荷,kW;Pf为送风机的功率,kW。
1.1.4无组织渗风负荷
(5)
式中Qi为无组织渗风负荷,kW;G1、G2分别为通过出入口进入站厅和通过屏蔽门进入站台的无组织渗风量,m3/h;Δh1为室外与站厅空气的比焓差,kJ/kg;Δh2为隧道与站台空气的比焓差,kJ/kg。
1.1.5围护结构得热量
屏蔽门传热量计算公式为
QPSD=KPSDFPSD(tt-tp)
(6)
式中QPSD为屏蔽门传热量,kW;KPSD为屏蔽门的传热系数,kW/(m2·℃);FPSD为屏蔽门面积,m2;tt、tp分别为隧道和站台空气温度,℃。
对站厅层和站台层分别计算外围护结构传热量。站台层多位于地下15 m左右,土壤温度可视为恒定,因此采用稳态计算方法,其外围护结构得热量的计算公式为
(7)
式中Qep为站台层外围护结构传热量,kW;α为墙体表面传热系数,W/(m2·℃);δ1、δ2分别为混凝土和土壤的厚度,m;λ1、λ2分别为混凝土和土壤的导热系数,W/(m·℃);F1为站台层外围护结构面积,m2;ts为恒温层土壤温度,℃。
站厅层多位于地下5~10 m,气温年波动对地层温度的影响不可忽略,采用逐月土壤平均温度进行计算,其外围护结构得热量的计算公式为
(8)
式中Qeh为站厅层外围护结构传热量,kW;F21、F22分别为站厅层侧墙和顶板面积,m2;tsx、ts0分别为地下埋深x处和地表的月平均温度,℃;th为站厅空气温度,℃;δ3为站厅层混凝土顶板与地表的距离,m。
1.1.6站内设备散热量
设备散热量主要由照明设备、垂直交通系统设备和站内其他设备(包括检票闸机、售票机、显示屏等)组成。照明设备散热带来的冷负荷由其功率计算,垂直交通系统的设备散热量根据“垂直交通系统能耗模型”计算,站内其他设备带来的冷负荷根据其功率近似计算。
1.2 系统能效模型
对于空调季,通风空调系统能效比计算公式为
(9)
(10)
式(9)、(10)中EERr、EERt分别为冷源和空调末端的能效比;WTFchw、WTFcw分别为冷水和冷却水的输配系数;COP为冷水机组性能参数。
对于通风季,通风空调系统能效比即为空调末端能效比。
2 地铁车站照明系统能耗原理模型
由于地下空间难以利用自然采光进行照明,因此照明系统基本不受自然采光的影响,其运行模式和能耗相对稳定,能耗计算公式为
(11)
式中EL为照明系统能耗,kW·h;PL为照明功率密度,W/m2;F为照明面积,m2;τL为照明系统运行时间,h。
3 地铁车站垂直交通系统能耗原理模型
垂直交通系统能耗计算公式为
ETR=PTRτTR
(12)
式中ETR为垂直交通系统能耗,kW·h;PTR为垂直交通系统设备运行功率,kW;τTR为垂直交通系统运行时间,h。
垂直交通系统设备包括直梯和自动扶梯,由于两者用能特征和工作模式差异较大,需要分别建立模型进行计算。
3.1 直梯模型
直梯的工作模式包括使用模式和待机模式:直梯在使用模式下工作功率大、时间短,其工作时间取决于列车到站次数和乘客人数,计算公式见式(13);而待机模式下工作功率小、时间长,其工作时间为直梯工作总时长减去使用模式下的工作时长。
(13)
式中τli_op为直梯在使用模式下的工作时间,h;f为单次列车到站直梯的运行频次;n为列车到站次数;Hli为直梯的提升高度,m;vli为直梯的额定运行速度,m/s。
3.2 自动扶梯模型
地铁车站自动扶梯的控制策略多为感应变频控制,即使用传感器监测是否有乘客靠近,以此作为模式切换的信号。采用感应变频控制的自动扶梯工作模式包括额速有载模式、额速空载模式和低速空载模式。
3.2.1上行扶梯
在地铁车站中,出站乘客比较集中,列车每次到站后会有乘客下车搭乘上行扶梯,扶梯开始以额速有载模式运行,当乘客全部离开后,上行扶梯经过一定的时间切换为低速空载模式。上行扶梯额速有载模式的运行时间与列车到站次数和单次下车人数有关,额速空载模式的运行时间可由模式切换时间确定,低速空载模式与列车到站时间间隔有关。
(14)
τup_ur=nτsw
(15)
τup_ul=τesc-τup_mr-τup_ur
(16)
式(14)~(16)中τup_mr、τup_ur、τup_ul分别为额速有载、额速空载和低速空载模式下上行扶梯的运行时间,h;a为单个台阶站立人数;h为台阶高度,m;Hesc为扶梯提升高度,m;vesc为扶梯额定速度,m/s;β为扶梯倾斜角度,°;τsw为额速模式与低速模式切换时间,h;τesc为扶梯工作时间,h。
上行扶梯各模式下运行功率之间的关系为
Pup_mr=ηup(Pesc-Pup_ur)+Pup_ur
(17)
(18)
(19)
(20)
式(17)~(20)中Pup_mr,Pup_ur分别为额速有载和额速空载模式下上行扶梯的运行功率,kW;ηup为上行扶梯负载率;Pesc为自动扶梯额定功率,kW;m0和k为中间变量。
3.2.2下行扶梯
下行扶梯能耗的计算方法与上行扶梯相似,差异仅在于模式切换次数的计算。由于地铁车站进站客流比较分散,根据实地调研作如下假设:1) 乘客分批进站,下行扶梯运送完一批乘客之后再运送下一批;2) 如果运送两批乘客的时间间隔大于扶梯的模式切换时间间隔,则自动扶梯会在运送完一批旅客之后切换为低速空载模式运行,否则不切换。根据计算时段内的总进站人数和连续进站人数,采用式(21)计算下行扶梯运送的乘客批次数。
(21)
式中Agr为下行扶梯运送乘客批次数;b为连续进站人数。
考虑到乘客进站的随机性,下行扶梯在计算时段内的模式切换次数可能为1、2、…、Agr。选取平均值(Agr+1)/2作为切换次数,同时需要保证扶梯额速运行的时间短于总工作时间。由此,下行扶梯的模式切换次数可由式(22)计算。
(22)
式中nd_sw为下行扶梯的模式切换次数;τd_mr为额速有载模式下下行扶梯的运行时间,h。
4 地铁车站分项能耗模型的简化
4.1 敏感性分析
上述能耗原理模型给出了根据地铁车站实际运营状况计算主要用能系统能耗的方法,可以用于各系统节能运行状况的评估和节能潜力的挖掘。但是模型输入参数复杂,现场调研和数据收集工作量大,存在实际工程中难以直接应用的问题:1) 通风空调系统模型需要64个输入参数,垂直交通系统模型需要25个输入参数,输入参数多,数据调研工作在工程实践中的开展难度大;2) 由于施工和维护成本的问题,分项能耗数据质量差,部分设备运行数据无法准确获得。因此,需要对地铁车站通风空调系统和垂直交通系统的能耗原理模型进行简化,从而实现将模型在全国不同气候区不同类型的地铁车站中进行大规模应用,进行节能运行的评估和节能潜力的挖掘。
敏感性分析通过量化输入对输出的影响能够识别最有影响的参数[11],确定哪些输入参数能够固定在其分布域内的任意值而不对输出结果影响太大[12],从而起到简化模型的作用。本文对地铁车站通风空调系统、垂直交通系统能耗模型进行了敏感性分析,得到了各输入参数的重要性排序,结果如图1和图2所示。可以看出,对于通风空调系统和垂直交通系统能耗模型而言,仅有少量的输入参数具有较大的敏感性指标,多数输入参数对模型输出结果的影响程度较低,模型存在简化的可能。
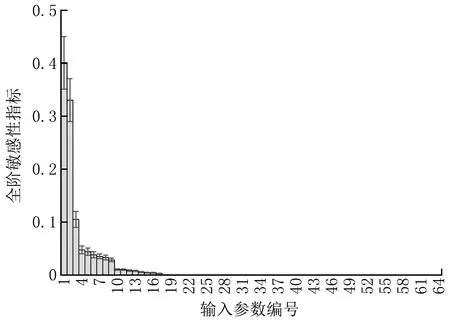
图1 通风空调系统能耗原理模型各输入参数的敏感性指标
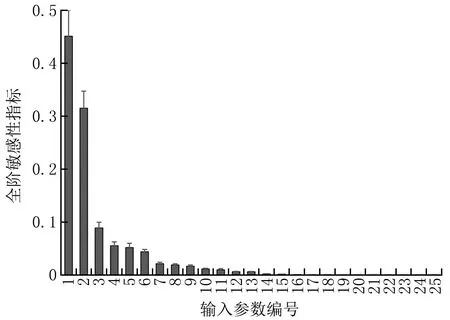
图2 垂直交通系统能耗原理模型各输入参数的敏感性指标
4.2 模型简化研究
基于敏感性分析的结果,对能耗原理模型进行了简化研究,简化过程如下:对于敏感性指标排序靠前的重要参数,其输入值采用对实际各车站详细调研获取的数据,而其他参数的输入值采用已有调研获取的社会平均水平值(不再逐个车站获取数据);探究不同的详细调研输入参数数量对能耗模型精度的影响,简化模型精度评价指标采用均方根误差(RMSE)和均方根误差变异系数(CV-RMSE)。
(23)
(24)

4.2.1通风空调系统能耗简化模型
通风空调系统能耗原理模型共64个输入参数,包括建筑信息、设备参数、客流情况、站内环境参数等。采用不同详细调研输入参数数量的简化模型与原理模型的均方根误差变异系数如图3所示。可以看出,采用15个详细调研的输入参数,其他参数采用社会平均水平值,简化模型的均方根误差变异系数为7.6%,对应的均方根误差为27.5 kW·h。进一步增加模型输入参数数量对模型精度提升的作用有限。综合考虑模型精度和实际工程收集数据的难度,后续推广使用的地铁通风空调系统能耗简化模型拟采用表1中列出的15个输入参数,可以分为5类:1) 站外环境参数;2) 车站新风及渗风量;3) 设备能效;4) 站内环境参数;5) 客流信息。
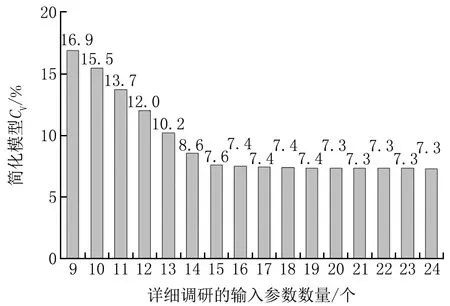
图3 不同输入参数数量下通风空调系统能耗简化模型的精度
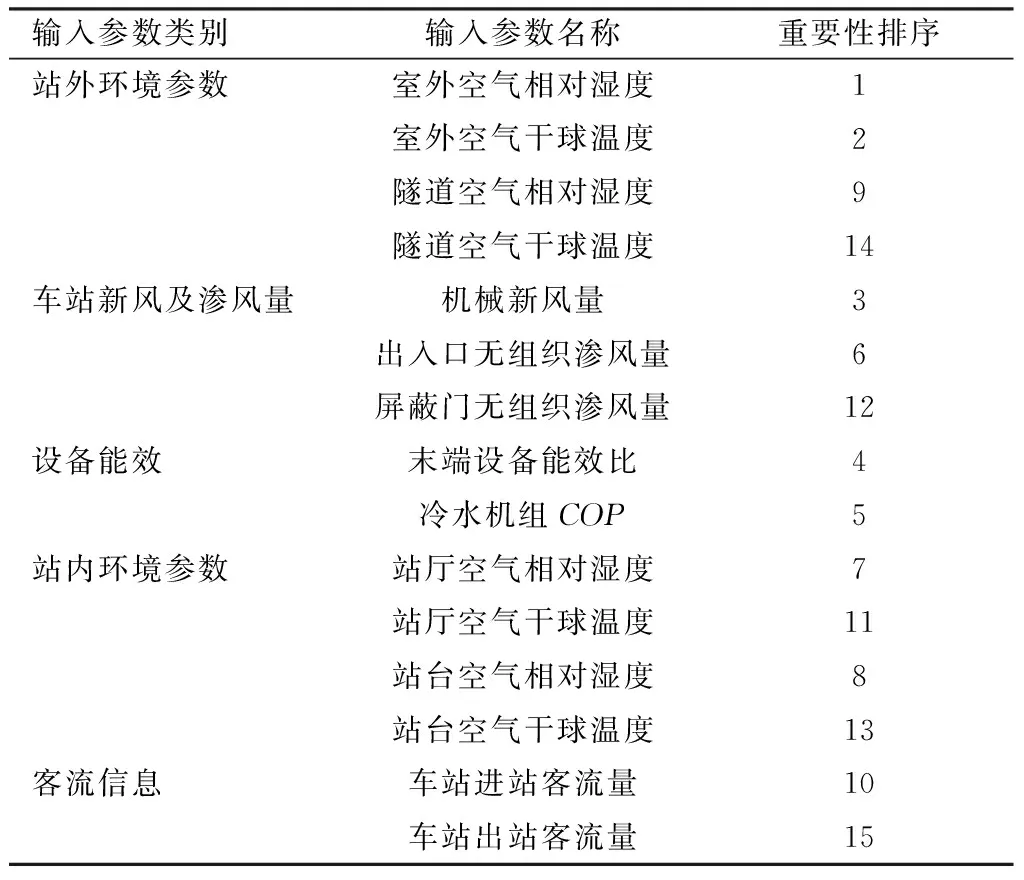
表1 通风空调系统能耗简化模型的输入参数
以夏热冬冷地区某地下2层标准岛式车站为例,采用简化模型和原理模型对空调季通风空调系统能耗进行模拟,结果如图4所示。结果显示,简化模型与原理模型的最大相对误差为8%,平均相对误差为2%,这一精度在工程应用领域可接受。

图4 某车站空调季典型日能耗简化模型与原理模型对比
4.2.2垂直交通系统能耗简化模型
垂直交通系统能耗原理模型共25个输入参数,包括列车到站情况、客流信息、电梯参数、建筑信息等。采用不同详细调研输入参数数量的简化模型与原理模型的均方根误差变异系数如图5所示。结果显示,采用11个详细调研的输入参数,其他参数采用社会平均水平值,简化模型的均方根误差变异系数为7.4%,对应的均方根误差为2.1 kW·h。进一步增加输入参数数量,模型精度可以进一步提高,采用18个详细调研的输入参数时,模型的均方根误差变异系数仅为3.3%。但是考虑到垂直交通系统能耗在地铁车站中的占比约为14%~21%,采用11个输入参数的简化模型精度可接受,后续推广使用的垂直交通系统能耗简化模型拟采用表2中列出的11个输入参数,可以分为3类:1) 列车运营信息;2) 客流信息;3) 扶梯参数。

图5 不同输入参数数量下垂直交通系统能耗简化模型的精度

表2 垂直交通系统能耗简化模型的输入参数
在夏热冬冷地区某地下2层标准岛式车站中应用垂直交通系统能耗简化模型和原理模型进行模拟,结果如图6所示。可以发现,简化模型与原理模型的最大相对误差为4%,平均相对误差为1%,这一精度在工程应用领域可接受。

图6 某车站典型日垂直交通系统能耗简化模型与原理模型对比
5 结语
随着地铁车站用电量的不断增长,需要对地铁车站主要用能系统的能耗进行模拟和分析,以评估车站的用能水平和节能潜力。基于此需求,本文研究了基于用能系统运行特征和运营数据的地铁车站分项能耗原理模型,包括通风空调、照明和垂直交通系统能耗模型。进而针对实际工程中输入参数数据收集难度大的问题,通过敏感性分析提取了模型的重要输入参数,对原理模型进行了简化研究。简化模型中仅有少量输入参数采用对实际各车站详细调研获取的数据,而其他输入参数采用已有调研获取的社会平均水平值。研究发现,简化的通风空调系统和垂直交通系统能耗模型分别可采用15个和11个详细调研的输入参数,简化模型的均方根误差变异系数分别为7.6%和7.4%,符合工程应用的精度要求。该简化模型将工程应用中数据收集的工作量降低了60%以上,从而能够实现将能耗模型在全国不同气候区各城市的地铁车站中进行大规模应用,用于快速评估车站的运行状况和节能潜力。
