锥面二次包络环面蜗轮副数字化建模与求解算法

刘 志，匡 鑫，王青萌，卢 红

(1.黄冈师范学院 机电与汽车工程学院，湖北 黄冈 438000；2.武汉理工大学 机电工程学院，湖北 武汉 430070)

包络成型蜗轮传动副在机械装备中应用广泛，尤其用于各种精密和重型传动。复杂的包络运动使此类蜗轮副齿廓通常为空间复杂曲面，也造就了其零件具有传动平稳、啮合紧凑、效率高、承载强、寿命长等优异性能[1–2]。此优异的啮合性能对蜗轮副齿面精度和啮合关系要求十分严格[3–4]，由建模方法和求解算法导致的几何误差及啮合偏差，将直接降低蜗轮副在工程中的应用性能[5–6]。

数字包络法和解析法是复杂包络成型面的主要表征方法。数字包络法模拟包络面的成型过程，实施布尔运算获取包络面实体模型。数字包络法操作简单，但缺乏包络母面与工件之间的映射关系，无法得到啮合点云的坐标信息，不适用于包络线的计算[7]。对生成的系列离散化曲面片进行重构获取光滑曲面模型过程中，不可避免存在重构误差。此建模方法精度难以保证，常用于蜗轮副啮合性能的宏观分析[8]。

解析法能获取较高的建模精度，但涉及复杂的数学运算与模型求解[9]。陈燕等[10]为探究渐开线包络环面蜗杆基本参数对传动性能的影响，运用啮合理论等方法推导了蜗杆副的啮合方程和齿面模型，分析了传动比、法向模数等主要建模参数对传动性能的影响，给出了接触斑点的分布区域。邓星桥等[11]对滚子包络蜗杆传动机构展开了系统研究，运用齿轮啮合理论构建了其啮合方程、接触线方程以及诱导法曲率等，并运用MATLAB对啮合模型进行了数值计算分析。赵超飞等[12]对环面蜗杆–圆柱斜齿轮传动机构开展了建模研究，通过蜗杆与斜齿轮的几何设计参数建立了蜗杆与斜齿轮的3维模型，探究了此类传动机构的接触性能。张敬孜等[13]研究了变齿厚内齿轮包络鼓形蜗杆传动的接触线方程、蜗杆蜗轮齿面方程、一类和二类界限曲线的数学模型，分析了蜗轮转动角度、工作角度等主要设计参数间的关联，并开发了蜗杆传动装置。王凯等[14]研究了无侧隙端面啮合蜗杆传动的啮合方程，在MATLAB环境中拟合得到蜗杆螺旋线，以此获取蜗杆3维模型。Liu等[15]对包络成型面的一般表征方法做了阐述，运用运动学和空间坐标转化方法等数学工具构建了一次、二次包络成型面的一般数学模型，以工程中典型包络面为建模对象进行了实例验证。刘志等[16–17]研究了平面一次包络环面蜗杆和二次包络环面蜗轮的数字建模方法，推导了蜗杆和蜗轮的齿面啮合方程和接触线方程，计算了蜗杆和蜗轮的啮合点云。关于锥面包络环面蜗轮传动副的研究相对较少，程福安等[18]较早提出了锥面包络蜗轮副传动形式，阐明了此类蜗轮传动副的成型原理，建立了建模活动标架，推导了蜗杆齿廓啮合方程，并分析了二次包络蜗轮的成型方法，为后续研究提供了基础。赵先锋等[19]采用解析法与数字包络法相结合的手段对锥面包络蜗杆开展了建模研究，通过构建活动标架，运用啮合理论建立了蜗杆齿面的轴面截形曲线和轴向螺旋线，在Solidworks环境下获得了蜗杆实体模型。王志刚等[20]研究了双锥面包络环面蜗杆齿廓啮合方程的构建方法，阐述了蜗杆传动的轴向截面齿形的计算方法，并提出了理论齿形的求解思路。席晨如[21]研究了锥面包络蜗杆传动的啮合理论，构建了蜗杆的啮合函数，建立了蜗杆方程和蜗轮齿面方程，分析了蜗杆和蜗轮齿面接触线的分布。

包络蜗杆传动机构具有优异的啮合性能和广阔的应用前景，学者们围绕其数字建模和性能分析开展了广泛研究。限于成型过程和啮合齿面的复杂性，现有研究主要集中于讨论传动副的数字建模理论，缺乏有效求解算法对理论模型进行全面求解，模型的有效性和准确性缺乏验证。对于锥面二次包络环面蜗轮，其建模理论研究也相对偏少。精密数字模型和模型求解算法的缺乏制约了蜗轮副的高精度数字制造及高性能应用。作者基于啮合理论等数学工具系统推导锥面包络蜗杆和二次包络蜗轮的数字模型。设计数字模型求解算法，获取蜗杆和蜗轮的全部瞬时接触线和3维数字化模型。研究结果可为此类蜗轮传动副的高精度制造和高性能应用提供模型基础。

1 锥面包络环面蜗轮副成型原理

锥面包络蜗杆的产型母面为一斜置锥形砂轮，砂轮与另一锥形刀架相固联。母面砂轮随刀架转动并对蜗杆毛坯做包络运动，生成蜗杆齿廓。成型后的蜗杆作为新的母面包络蜗轮毛坯，二次包络产生蜗轮齿廓，如图1所示。

图1中，刀架底圆与蜗轮基圆重合。刀架角速度为ω3，蜗杆角速度为ω2，蜗轮角速度为ω3，i12为蜗轮副传动比，ω2/ω3=i12。O2O3为蜗轮副的中心距a，母面砂轮底圆中心与刀架切线长为h。

图1 锥面包络环面蜗轮副成型过程Fig. 1 Forming process of cone generated double-enveloping hourglass worm wheel pair

2 锥面一次包络环面蜗杆数字模型

2.1 锥面一次包络环面蜗杆建模标架

根据图1成型原理，建立如图2所示的蜗杆建模标架。其中，S1(O1−x1y1z1)为 锥形母面砂轮坐标系，S3(O3−x3y3z3) 为刀架初始静坐标系，S3i(O3−x3iy3iz3i)为刀架动坐标系，S2(O2−x2y2z2)为 蜗杆初始静坐标系，S2i(O2−x2iy2iz2i)为蜗杆动坐标系。上述坐标系中坐标分别表示 为 [x1,y1,z1]T、 [x3,y3,z3]T、[x3i,y3i,z3i]T、 [x2,y2,z2]T、[x2i,y2i,z2i]T。

图2 蜗杆数字建模标架Fig. 2 Modeling frame of the worm

2.2 蜗杆右侧工作齿廓模型

锥形母面砂轮坐标系统如图3所示，α1为母面砂轮锥面倾角，R1为砂轮底圆半径，圆O为砂轮任意截面，M为截面上任一点。

图3 锥形母面砂轮建模坐标系统Fig. 3 Coordinate system for modeling frame of cone generator

锥母面砂轮S1(O1−x1y1z1)中啮合点M矢量：

M在S1(O1−x1y1z1)中的法向量：

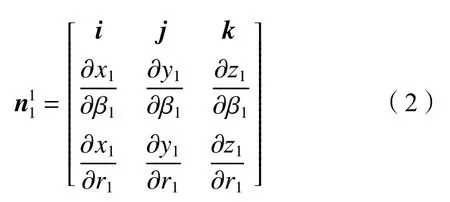
式中，RotY表示绕Y轴的旋转变换，TraX表示沿X轴的平移变换，其他类同。

根据运动学方法，空间两构件的相对运动速度计算如下：

锥母面砂轮与蜗杆相对运动速度矢量在刀架静系S3(O3−x3y3z3)中表示为：

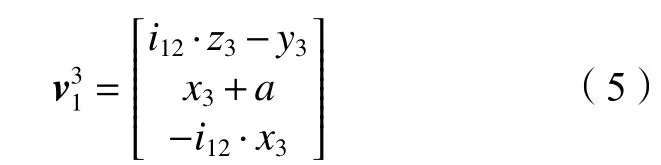
根据空间啮合理论[2]，n·v=0，联立式（3）和（5），建立刀架动系S3i(O3−x3iy3iz3i)中蜗杆右侧齿廓啮合方程：

将式（6）确定的啮合点从S3i(O3−x3iy3iz3i)转换至蜗杆动系S2i(O2−x2iy2iz2i)，可获取蜗杆动系中蜗杆右侧工作齿廓数字模型：

式（7）为多元非线性模型，有3个参变量β1、r1、φ3。其中，β1、r1为锥母面砂轮截面参数，φ3为刀架转动角度参数，φ3的取值区间可由包络条件确定。

2.3 蜗杆左侧工作齿廓模型

蜗杆左右两侧齿廓成型过程相同，锥母面砂轮的起始包络位置不同。记蜗杆右、左两侧工作齿廓锥母面砂轮起始包络位置夹角为ε0，由蜗杆右侧工作齿廓模型，可构建蜗杆左侧工作齿廓数字模型：

2.4 蜗杆齿底齿顶圆环模型

蜗杆相关参数如图4所示。

根据图4所示的几何与参数关系，构建蜗杆齿顶圆环母线方程：

图4 蜗杆齿顶齿底圆环及相关参数示意图Fig. 4 Sketch map of addendum，bottom and related parameters of worm

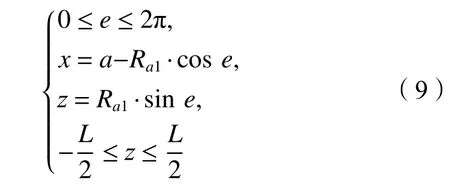
蜗杆齿底圆环母线方程：

式中，e为角度参数，Ra1为蜗杆齿顶圆弧半径，L为蜗杆工作齿廓轴向长度，Rf1为蜗杆齿底圆弧半径。

2.5 蜗杆齿面模型约束条件

式（9）、（10）是具有解析表达的旋转方程，不存在其他约束条件。式（7）、（8）具有齿廓边界和包络边界，结合图3和4构建约束条件如下：

3 锥面二次包络环面蜗轮数字模型

3.1 锥面二次包络环面蜗轮建模标架

包络成型的蜗杆对蜗轮毛坯以同样的条件做第二次包络运动，形成蜗轮齿面。蜗轮齿面由蜗轮右左两侧工作齿廓、齿底圆环面和齿顶圆环面构成。蜗轮右、左工作齿廓为复杂的二次包络面，如图5所示，其工作区域包括一次工作区和二次工作区[16]。

图5 锥面二次包络蜗轮齿面构成Fig. 5 Forming of double-enveloping worm wheel surface

根据图1成型原理，建立如图6所示的二次包络环面蜗轮建模标架。包络工具蜗杆的角速度为，蜗轮角速度为，蜗杆转角为蜗轮转角为，有/=i12，φ′2/φ′3=i12。S2(O2−x2y2z2)为 蜗杆静系，S2i(O2−x2iy2iz2i)为 蜗 杆 动 系，S3(O3−x3y3z3) 为 蜗 轮 静 系，S3i(O3−x3iy3iz3i)为蜗轮动系，4个坐标系中啮合点坐标分别为[x2,y2,z2]T、[x2i,y2i,z2i]T、[x3,y3,z3]T、[x3i,y3i,z3i]T。

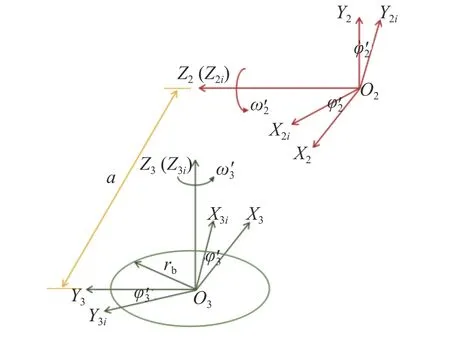
图6 蜗轮建模标架Fig. 6 Modeling coordinate frame of worm wheel

3.2 蜗轮右侧工作齿廓模型

蜗轮成型过程中，根据如图6所示的坐标标架，将式（2）确定的法矢量转换至蜗杆动系，得到S2i(O2−x2iy2iz2i)中的法矢量：

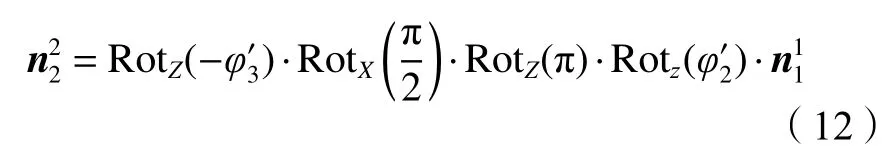
由式（4）可得S2i(O2−x2iy2iz2i)中蜗杆与蜗轮的相对运动速度矢量：

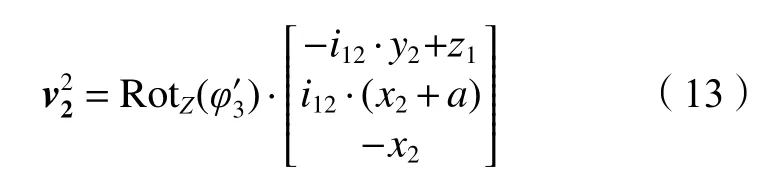
根据空间啮合理论[2]，n·v=0，结合空间坐标转换方法，可得在蜗杆动系S2i(O2−x2iy2iz2i)中的蜗轮右侧齿廓啮合方程：

将式（14）确定的满足啮合理论的坐标点转换至蜗轮动系S3i(O3−x3iy3iz3i)，可得蜗轮右侧工作齿廓数字模型：

显然，φ3=+2kπ(k∈Z)时，式（15）与（7）等价，式（7）确定的解即是式（15）的解。这是蜗杆齿廓点云在蜗轮工作齿廓上的复现，形成了蜗轮工作齿廓的一次接触区。φ3≠+2kπ(k∈Z)时，式（15）的其他解形成了蜗轮工作齿廓的二次接触区。

3.3 蜗轮左侧工作齿廓模型

类比蜗杆左侧齿廓建模方法，结合蜗轮齿廓啮合方程与空间坐标转换矩阵，可得蜗轮动系S3i(O3−x3iy3iz3i)中蜗轮左侧齿廓数字模型：

类似地，式（16）有两部分解，蜗轮左侧工作齿廓也由两部分区域构成。

3.4 锥面二次包络环面蜗轮齿底齿顶圆环模型

锥面二次包络环面蜗轮齿顶、齿底为圆环，其由圆环母线旋转而成。

蜗轮齿顶圆环母线方程：

蜗轮齿底圆环母线方程：

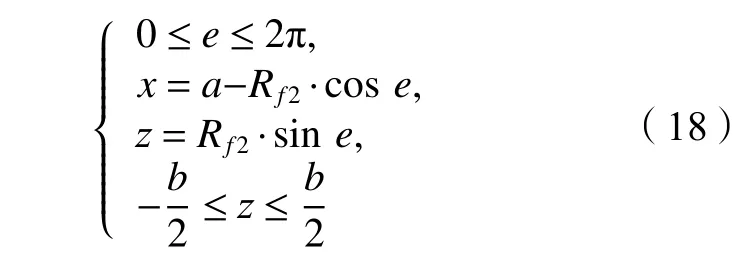
式（17）、（18）中，e为角度参数，Ra2为蜗轮齿顶圆弧半径，b为蜗轮工作齿宽，Rf2为蜗轮齿底圆弧半径。

3.5 蜗轮齿面模型约束条件

式（17）和（18）是具有解析表达的旋转方程，不存在其他约束条件。式（15）和（16）具有齿廓边界和包络边界，约束条件如下：

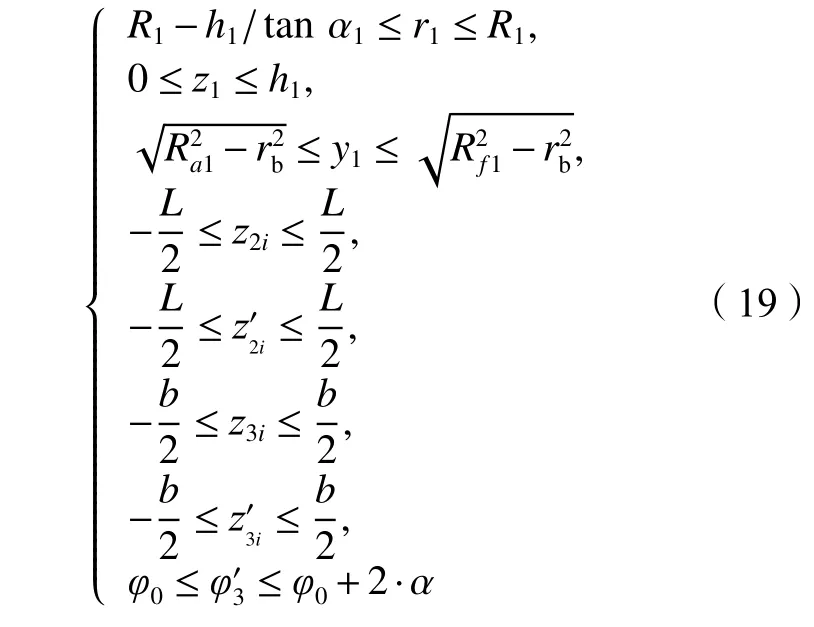
4 蜗轮副齿面模型求解算法

4.1 蜗杆齿面求解算法

式（7）～（11）组成锥面包络蜗杆整体齿面模型，其中，式（9）～（11）表征的蜗杆工作齿廓为带多个约束条件的非线性模型，需设计求解算法。式（7）确定的蜗杆右侧齿廓模型，含有3个参变量β1、r1、φ3，其中：φ3为刀架转动角度参数，有其取值区间；β1最大取值区间为一个圆周。根据蜗杆基本参数计算包络角度φ3的取值区间后，在其区间内将φ3等值离散，每一离散的φ3对应一条蜗杆齿廓接触线。在β1的圆周取值区间内，继续将其等值离散，通过蜗杆齿廓啮合方程获取系列满足啮合条件的(β1，r1)组合，以构成每一包络瞬间的接触点。算法框图如图7所示。

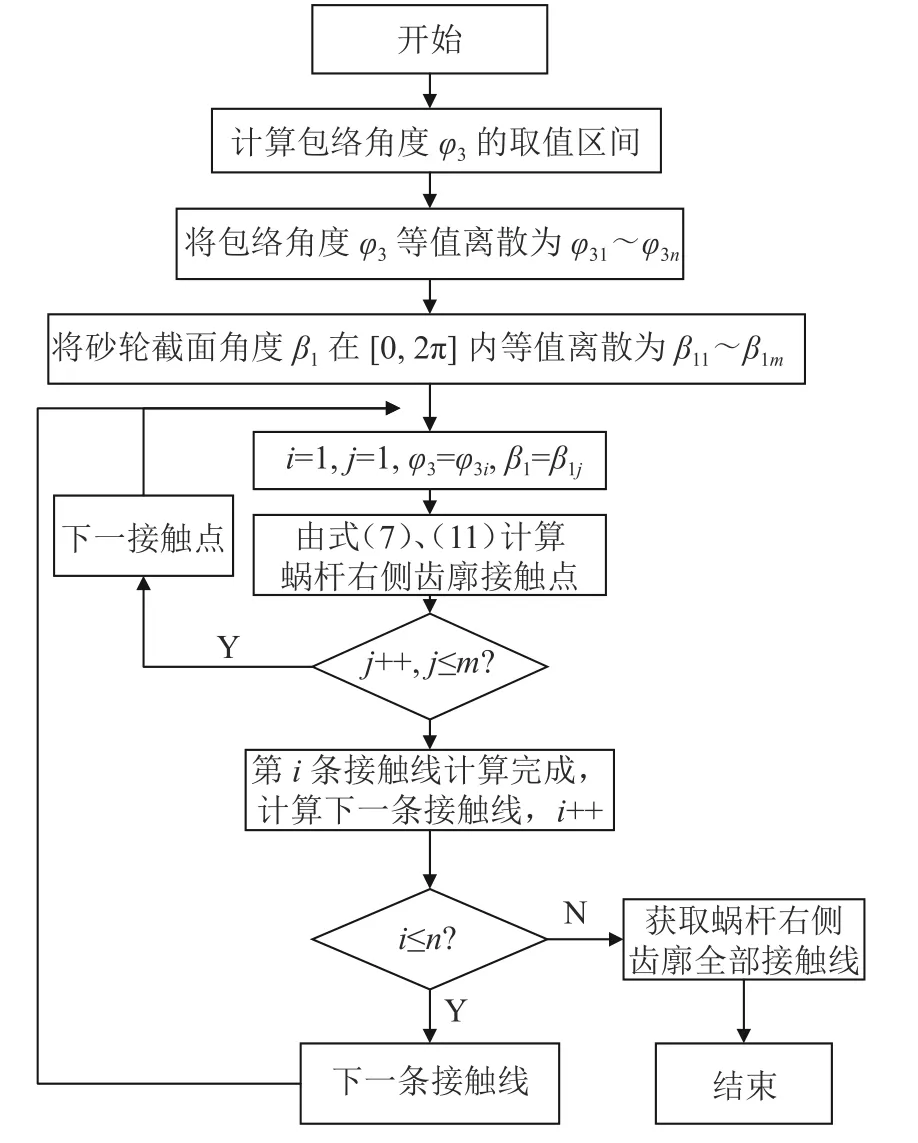
图7 蜗杆右侧工作齿廓模型求解算法流程图Fig. 7 Flow chat of solving algorithm for the tooth profile model of the right side of the worm

蜗杆左侧工作齿廓模型求解算法类同。

4.2 蜗轮齿面求解算法

式（12）～（19）组成锥面二次包络环面蜗轮整体齿面模型，式（15）～（16）和（19）表征的蜗轮工作齿廓为带多个约束条件的多元非线性模型，尤其涉及蜗轮二次接触区的计算更为复杂。针对式（15）确定的蜗轮右侧齿廓模型，设计求解算法如图8所示。

图8 蜗轮右侧工作齿廓模型求解算法流程图Fig. 8 Flow chat of solving algorithm for thetooth profile model of the right side of the worm wheel

蜗轮左侧工作齿廓模型求解算法类同。

5 锥面二次包络环面蜗轮副建模实例

针对锥面二次包络环面蜗轮传动副建模方法及模型求解算法，结合工程实例，给出实例验证。某锥面二次包络环面蜗轮副传动条件：中心距400 mm，蜗杆头数为1，传动比40，模数为4。对其进行参数计算与数字建模。

5.1 锥面包络环面蜗轮副建模参数

根据蜗轮副传动条件，计算出蜗轮副其他几何参数与建模参数，主要参数如表1所示。

表1 蜗轮副主要几何参数与建模参数Tab. 1 Main parameters of the worm wheel pair

5.2 锥面包络环面蜗杆模型

根据蜗轮副几何参数与建模参数，由图7所示的算法可获取蜗杆工作齿廓接触线簇。各坐标系中的接触线计算样例如图9～11所示，4条接触样线对应包络角：φ31= 0.114 8，φ32=0.131 6，φ33=0.148 4，φ34=0.165 2。蜗杆工作齿廓全部接触线簇如图12～14所示。蜗杆齿底齿顶圆环母线如图15所示。

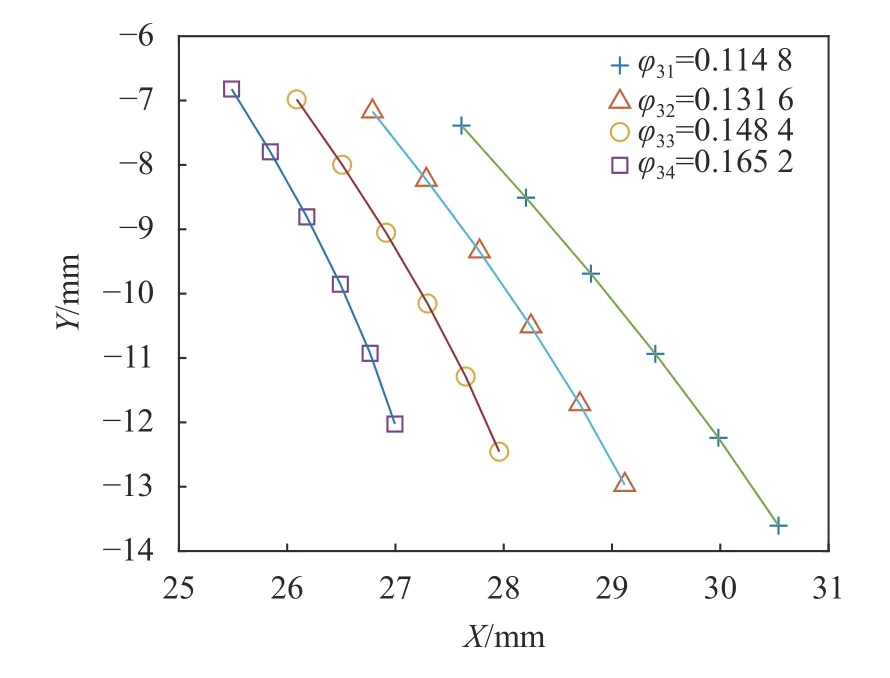
图9 锥面砂轮坐标系中接触线Fig. 9 Sample contact lines in cone generator coordinate

图10 锥面刀架坐标系中接触线Fig. 10 Sample contact lines in cone cutter coordinate

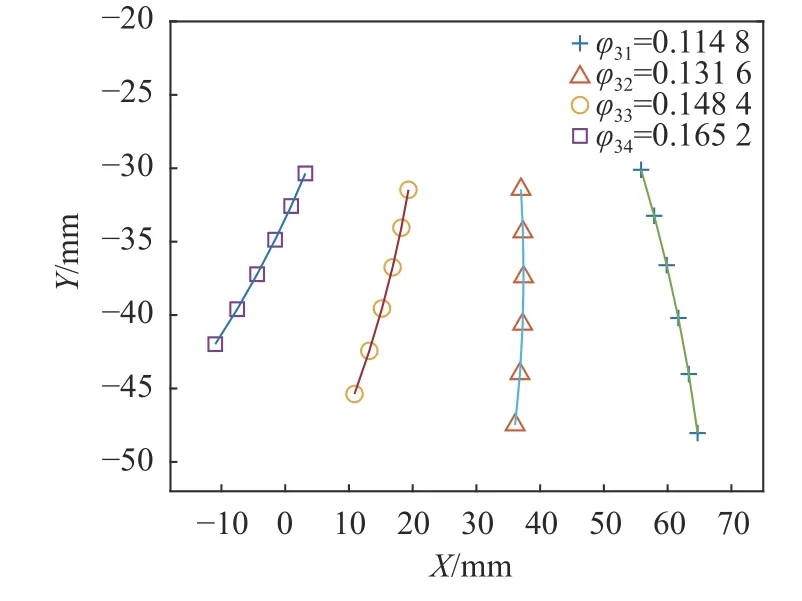
图11 蜗杆坐标系中接触线Fig. 11 Sample contact lines in worm coordinate

图12 蜗杆右侧工作齿廓全部接触线Fig. 12 All contact lines of the tooth profile model of the right side of the worm

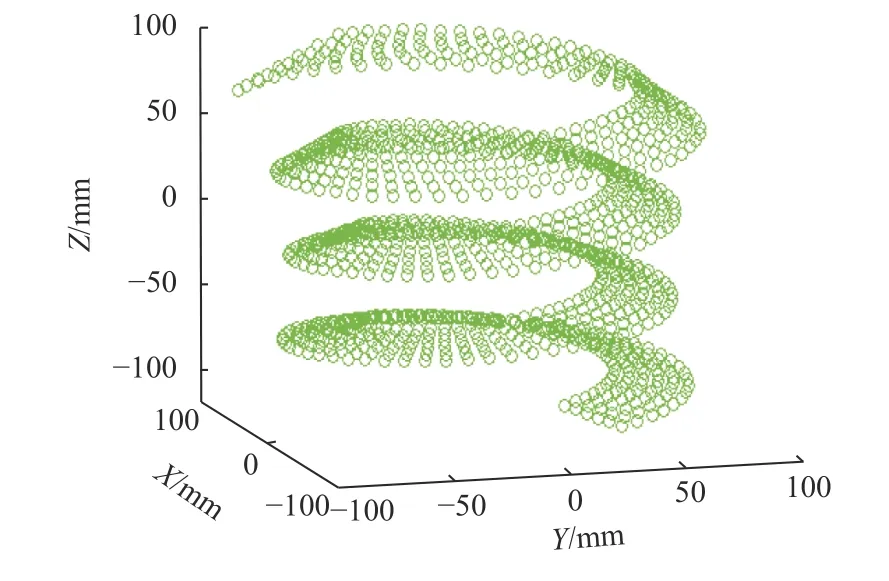
图13 蜗杆左侧工作齿廓全部接触线Fig. 13 All contact lines of the tooth profile model of the left side of the worm

图14 蜗杆工作齿廓全部接触线Fig. 14 All contact lines of worm working tooth

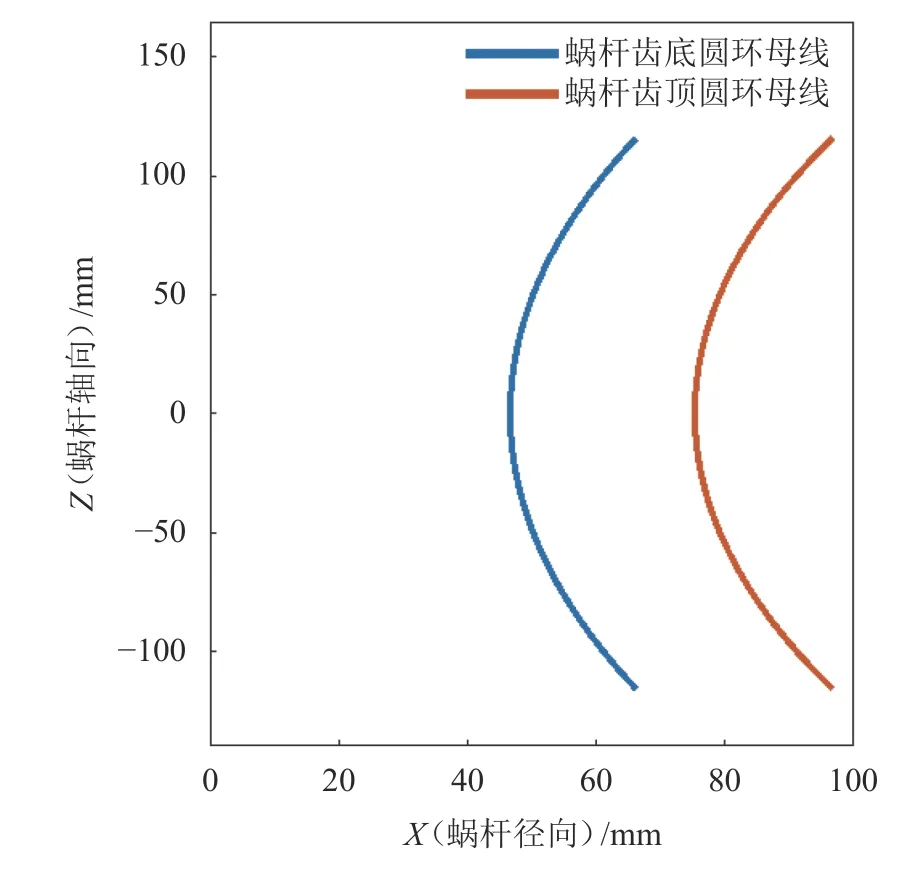
图15 蜗杆齿底齿顶圆环母线Fig. 15 Addendum and bottom generatrix of the worm

5.3 锥面二次包络环面蜗轮模型

根据蜗轮副几何参数与建模参数，由图8所示的算法求解式（15）、（16）与（19），可获取蜗轮工作齿廓全部接触线簇。将蜗杆齿廓接触线转换至蜗轮动系可得蜗轮齿廓一次接触区，蜗轮二次接触区的接触线计算样例如图16所示，蜗轮工作齿廓全部接触线簇如图17～19所示。

图16 蜗轮二次接触区接触线Fig. 16 Contact lines of second meshing zone of worm wheel

图17 蜗轮右侧工作齿廓全部接触线Fig. 17 All comtact lines of right side tooth of worm wheel

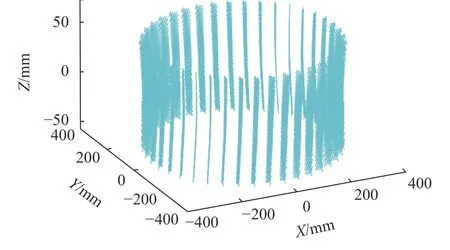
图18 蜗轮左侧工作齿廓全部接触线Fig. 18 All comtact lines of left side tooth of worm wheel

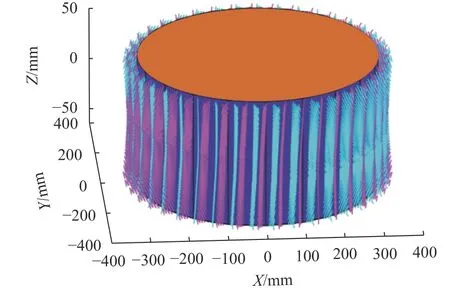
图19 蜗轮工作齿廓全部接触线Fig. 19 All contact lines of working tooth of worm wheel

由图17～18可知，蜗轮一次、二次接触区均为曲面，二者衔接完好，表明了理论模型和求解算法的准确性。蜗轮齿底齿顶圆环母线如图20所示。

图20 蜗轮齿底齿顶圆环母线Fig. 20 Addendum and bottom generatrix of worm wheel

5.4 蜗轮副计算精度分析

为验证蜗轮副求解算法，采用逆向包络法[16]分析蜗杆与蜗轮齿面点云计算精度。对每一计算的点云先分别逆向计算其在包络运动中对应的公法矢量与相对运动速度矢量，然后，计算公法矢量与速度矢量的数量级，将运算结果与零作差，衡量点云的计算误差。蜗轮副啮合点云误差如图21所示。蜗杆计算点云误差在10–9级，蜗轮点云误差在10–8级。

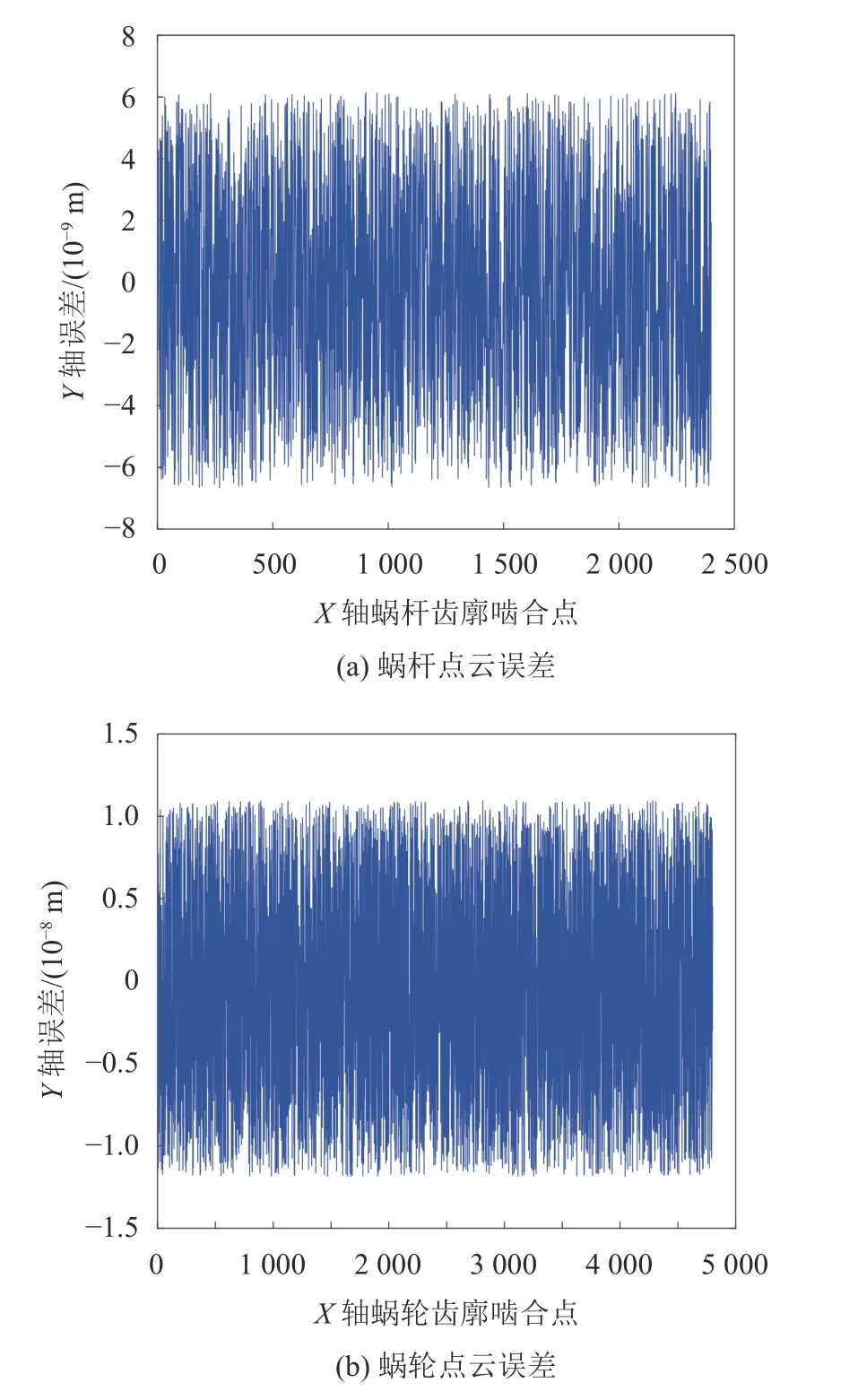
图21 蜗轮副点云误差Fig. 21 Calculation error curves of the worm wheel pair

5.5 蜗杆与蜗轮装配分析

将蜗杆与蜗轮工作齿廓接触线簇及环面母线导入Creo中，可构建蜗杆与蜗轮的3维数字化实体模型。参照图2所示的标架及啮合条件将蜗杆与蜗轮进行虚拟装配，如图22所示。按照成型条件将装配的蜗轮副进行虚拟运动仿真，仿真运行结果表明蜗杆与蜗轮啮合紧凑，无干涉现象，传动效果与理论相符，表明了蜗轮副模型的准确性和求解算法的有效性。

图22 蜗轮副装配模型Fig. 22 Assembly model of the worm wheel pair

6 结 论

构建了锥面包络环面蜗轮传动副的数字建模标架，推导了锥面包络环面蜗杆的啮合方程、接触线和齿面数字模型。以蜗杆齿面为母面，建立了二次包络环面蜗轮的啮合方程与齿面数字模型。建立了蜗杆与蜗轮数字模型的约束条件，设计了蜗杆与蜗轮齿面复杂数学模型的求解算法。给出了蜗轮副建模参数计算方法，通过MATLAB程序计算了蜗杆与蜗轮齿面全部非线性接触线簇。数字化建模实例表明建模方法和模型求解算法能够实现此类复杂蜗轮传动副的精确数字化实体建模，研究结果可为蜗杆、蜗轮滚刀和蜗轮的高精度数字制造提供模型基础，能有效提升传动副的传动性能和应用效果。