主成分分析法在气象数据分析中的应用探讨

罗 梅，任广红，王 刚，刘 梅，刘文洁，杨 涛

(1.贵阳市修文县气象局，贵州 贵阳 550299；2.贵州省农经信息中心，贵州 贵阳 550081；3.贵阳市气象局，贵州 贵阳 550001)

1 引言

近年来，极端灾害性天气频繁发生，其中，暴雨天气对人类的生产生活所产生的影响日益显著，暴雨灾害天气已成为气象领域研究的主要热点问题之一[1～3]。据相关研究表明，南方地区暴雨过程明显增多[4]；辽河区域暴雨高度集中在7～8月份，极端暴雨集中分布在辽西山丘迎风山区等地[5]。然而在对区域暴雨灾害的研究案例中，对小区域气象数据分析方法的实际应用的案例较少。目前，对于气象数据的统计分析常用的方法主要有判别分析、聚类分析、回归分析等，对于变量的分析主要有时域分析、谱分析、频域分析及耦合分析等[6]。

贵州省位于副热带东亚大陆的季风区，属于亚热带湿润温和型气候。贵州省修文县是黔中经济区和贵阳北部新区的重要节点城市，除西部边缘河谷切割较深外，相对高度多在150 m以内，谷宽水浅，槽谷和洼地较多，属于较典型的喀斯特丘陵地形。修文县境内海拔940～1610 m，平均海拔1290 m，气候属亚热带季风湿润区，冬无严寒，夏无酷暑，气候温和。

将统计分析方法应用于气象数据的分析已经较为普遍，然而将其应用于贵州小区域气象数据分析研究却少有。同时，虽然统计分析方法对气象数据的分析应用方法种类较多，但主成分分析方法应用于气象数据的分析案例却极少。然而，主成分分析是经验正交函数分解系列方法之一，是以大气变量场的数据样本为分析对象，把气象要素场分解为空间函数和时间函数；而时间函数则由空间点的线性组合所构成，称为主成分，这些主成分的前几个占有原空间点的总方差的很大部分。因此，研究主成分随时间变化的规律就可以代替对大气变量场随时间的变化研究。基于此，本文采用主成分分析方法，利用贵州省修文县气象台观测数据，详细阐明主成分分析方法在气象数据分析中的应用。

2 数据资料及研究方法

2.1 数据资料

论文研究数据资料主要来自于修文县气象台近10年地面气象观测资料。主要为逐月逐年降水数据。国家气象局依据24 h降水总量对暴雨等级进行划分，当总降水总量大于等于50.0mm且小于等于99.9 mm时，则计为“暴雨”；当总降水总量大于等于100.0mm且小于等于249.9 mm时，计为“大暴雨”；当总降水总量大于等于250.0 mm时，则计为“特大暴雨”。

本文采用的暴雨事件评价指标为：年暴雨日数、年暴雨量、年暴雨强度及年暴雨贡献率。年暴雨日数(d)指一年中发生暴雨以上天数之和；年暴雨量(mm)指一年中暴雨以上降水量之和；年暴雨强度(mm/d)指当年暴雨量与暴雨日数之比；年暴雨贡献率指当年暴雨量占总降水量的比值。

2.2 研究方法

本文主要研究方法为主成分分析方法及相关性分析方法，其中主成分分析作为主要的经验正交函数分解系列方法之一，又称为主分量分析。主成分分析方法能在保证信息损失量最小的前提下，尽可能提取数据的主要方面。近年来，随着多元统计方法的推广与普及，主成分分析又有了十分重要的应用，如程娴等[7]利用主成分分析对郑州市小蜂螨爆发风险等级进行评价；杨晓颖等[8]利用主成分分析对内蒙古脆弱性进行等级评价；荆瑞勇等[9]利用主成分分析对水稻品种品质进行综合评价。因此，主成分分析成为构造系统评估指数、对系统的指数进行评估排序的常用方法之一。应用Excel软件统计数据并计算年降雨量、年暴雨日数、年暴雨量、年暴雨强度、年暴雨贡献率；同时应用SPSS20统计分析软件进行主成分分析，对各暴雨指标进行排序，优选最主要的暴雨指标。

本文主成分分析法的具体步骤：①建立气象观测数据矩阵，对气象观测数据进行标准化处理；②建立相关系数矩阵，计算各主成分的特征值λ；③依据累积贡献率及特征值，确定所需主成分的个数；④计算主成分得分，然后依据主成分得分对各暴雨指标进行排序。

3 结果与分析

3.1 相关性分析

本文以贵州省修文县气象台近10年降水观测数据为样本，利用主成分分析法(PCA)对修文县近10年年降雨量、年暴雨日数、年暴雨量、年暴雨强度、年暴雨贡献率等进行排序评估。修文县辖5个街道、7个乡镇，选择具有代表性的龙场街道站点的数据为研究对象；确定以年降雨量(X1)、年暴雨日数(X2)、年暴雨量(X3)、年暴雨强度(X4)、年暴雨贡献率(X5)作为统计分析变量，如此得到一个5×10的原始样本数据矩阵。运用SPSS20统计分析软件进行相关性分析，得到暴雨指标间的线性相关系数矩阵(表1)。

表1 暴雨指标间的线性相关系数矩阵

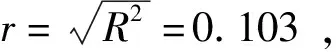
3.2 主成分分析

运用SPSS20统计分析软件进行主成分分析，主成分的方差贡献率、特征值和累计贡献率如表2所示。由表2知，原指标64.035%的信息量可由第一主成分进行反映。如果按照85%的判断标准，表中前2个主成分的累积方差贡献率已经高达86.911%，这表明前2个主成分已经能较好地反映气象观测数据所包含信息量的86.911%，从而实现了降维(表3)。

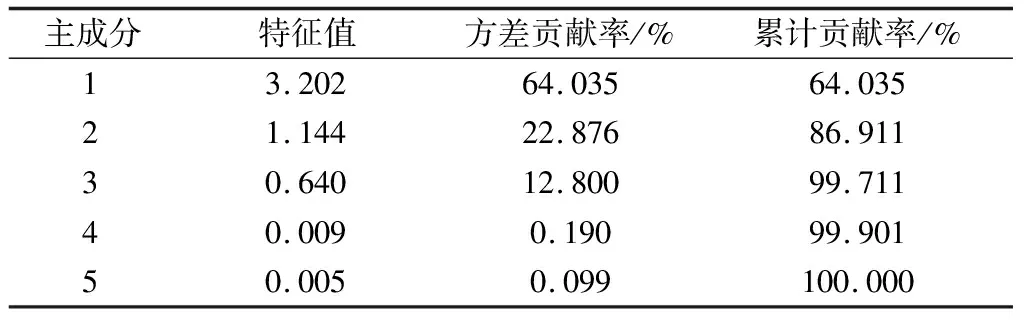
表2 各主成分的特征值、方差贡献率和累积贡献率

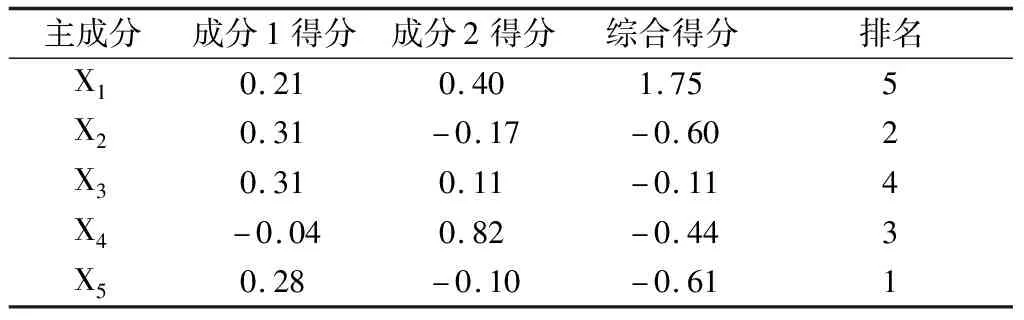
表3 主成分因子得分、综合得分排名

利用SPSS20统计分析软件计算主成分1和主成分2得分及综合得分，即可得出年降雨量(X1)、年暴雨日数(X2)、年暴雨量(X3)、年暴雨强度(X4)、年暴雨贡献率(X5)之间的排名，如表3所示。由表3知，将年降雨量(X1)、年暴雨日数(X2)、年暴雨量(X3)、年暴雨强度(X4)、年暴雨贡献率(X5)的综合得分由低到高升序排名依次为：年暴雨贡献率(X5)、年暴雨日数(X2)、年暴雨强度(X4)、年暴雨量(X3)、年降雨量(X1)。由此可知，在对暴雨的研究中，可优先选择年暴雨贡献率作为主要的暴雨指标，其次是年暴雨日数。

本文通过主成分分析，选择修文县龙场街道近10年降水数据，计算各暴雨指标：年暴雨日数、年暴雨量、年暴雨强度、年暴雨贡献率，采用主成分分析方法，优选出主要的暴雨指标；以期帮助修文提高城市防洪防涝能力，减少灾害损失，有助于提高暴雨灾害和洪涝灾害风险预警的能力，为贵州修文暴雨趋势的预测奠定基础，助力修文乡村振兴。

4 结论与讨论

气候变化会对生物多样性以及人类生产生活产生巨大影响；在近百年的时间里，全球气候变暖成为了地球气候变化的最主要特征。因此，气候的变化已经引起世界各国政府和人民的密切关注与重视。大量事实表明，我国的气候变化趋势与全球气候变化基本保持一致，而气候变化对极端天气如强降雨天气等具有一定的影响。因强降水天气具有突发性及季节性等特点，导致暴雨所引起的洪水灾害极为严重，对人民的生产生活都产生了极为严重的影响；同时，据IPCC第五次评估报告的内容，1951～2003年我国中高纬度地区的强降水事件频率有所增加[10]。因此，研究气候变化下强降水的时空变化势在必行。然而，对降水的研究中，暴雨降水集中、强度大、持续时间长，通常会引发山洪、泥石流、滑坡等灾害，因此，暴雨一直是气象工作者的重要研究内容之一[11，12]。同时，相关研究表明[13]贵阳市区域暴雨、年暴雨量及年降水量中暴雨贡献率呈增多趋势。

基于此，本研究对各暴雨指标进行计算，对各暴雨指标得分进行升序排序，依次为：年暴雨贡献率、年暴雨日数、年暴雨强度、年暴雨量、年降雨量。通过对气象数据统计分析，将相关性和主成分分析的多元统计思想应用到气象数据的统计应用中，从原始降水数据出发，发掘更多条有价值的信息，从而发现各暴雨指标之间的关联性；即年暴雨日数与年暴雨量、年暴雨贡献率之间呈显著正相关，年暴雨贡献率是最能反映暴雨事件的暴雨指标，其次是年暴雨日数。因此，在未来的研究中将进一步应用年暴雨贡献率及年暴雨日数分析贵州小区域范围内暴雨分布，并考虑对年暴雨贡献率和年暴雨日数的年际趋势和年际变化的特征及其二者与其他气象要素之间的相关性等做更深入的探讨研究。