谷物流量传感器敏感梁结构对测量精度的影响*

王一凡,汤建华,徐修祝

(1.常州纺织服装职业技术学院 机电学院,江苏 常州 213164；2.江苏大学 机械工程学院,江苏 镇江 212013)

0 引 言

基于双孔平行梁结构的力传感器具有良好的线性、滞后、重复性和抗偏载特性[1～3],在小量程的称重和测力领域应用广泛。近年来,随着精准农业与智能装备技术的发展,这类传感器在谷物测产以及经济作物测产等新领域也逐渐开辟了新的应用,通过检测谷物进仓时的冲量变化换算成单位面积的谷物产量,因此又称为冲量式谷物流量传感器。国外商业化的农机装备,如Micro Track公司、CASE IH公司和Ag Leader公司的联合收割机产量监测系统中的传感器均采用冲量式谷物流量传感器[4,5]。

冲量式谷物流量传感器测量的是一个动态的过程,因此要求传感器能够准确再现流量变化的过程。目前,国内外进行的相关研究主要集中在整体测量系统层面[6～9]。对传感器中弹性敏感元件结构的优化分析不多[10,11],还未见到对应变梁结构的优化设计研究。另外,在实际使用中这类传感器较多存在零点漂移的现象,Shoji K等人[12]研究了传感器的零漂补偿算法,使得测量的相对误差从补偿前的19 %,减小到补偿后的1.5 %,但没有分析零漂产生的原因。

本文主要对双孔平行梁式谷物流量传感器进行了动静态特性比较与分析,研究适合于动态冲击使用环境的传感器敏感梁结构,提高传感器在这种特殊应用环境下的测量精度和零点稳定性。

1 谷物流量传感器的设计与制作

双孔平行梁式传感器主要由双孔平行梁结构的弹性元件,粘贴在弹性元件上的应变片,以及由应变片及各种补偿电阻连接而成的惠斯顿电桥共同组成。如图1所示是两种不同结构的双孔平行梁传感器简图,设计量程都是8 kg,其主要差异在于双孔间距不同：结构A的中间双孔间距(17.3 mm)相对结构B(42 mm)更小；并且结构A中孔的最小壁厚为1.02 mm,结构B为1.56 mm。两种传感器的结构尺寸除上述敏感梁结构不同之外,其他外形尺寸和安装尺寸都完全一致。此外,在本文研究中,弹性元件的材料(硬铝2024—T4),Vishay公司350 Ω姆应变片以及其他导线、补偿电阻等零部件和惠斯顿电桥电路设计都保持相同,以方便后续试验比较时,减少其他干扰因素的影响。

图1 两种传感器的结构外形

此外,利用CreoSimulate有限元分析软件对这两种结构传感器进行了静态应力分析和模态分析,方便与后续试验结果进行对比分析。图2为结构A和结构B传感器在8 kg满载时的应力分布情况。表1列出了两种结构空载时的一阶响应频率和满载时的传感器挠度情况。

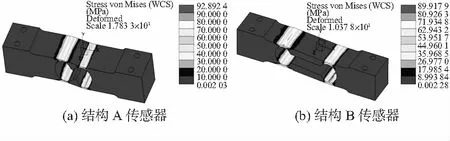
图2 二种结构传感器满载时的应力分布

表1 传感器一阶响应频率和挠度仿真结果

2 试验与分析

试验中,每种结构方案的传感器测试数量各为3只。

2.1 计量性能试验

在常温环境下,对结构A和结构B两种传感器进行了常温标定测试,测试方法按照OIML R60标准的测试方法执行。表2列出了两种结构的测试结果,结果表明两种传感器在静态的计量性能测试中都表现出极好的性能指标,而且在这些性能指标上,两种结构传感器的表现基本一致,没有显著差异。

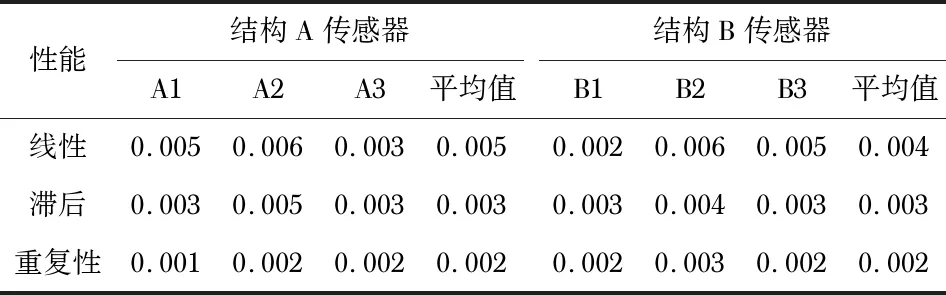
表2 传感器计量性能测试结果 %FS

2.2 安装敏感性试验

在收割机械工作时,振动和冲击是不可避免的,因此，如果传感器对从安装基座传递而来的这类附加应力敏感,就会对传感器的输出信号产生影响,从而影响测量精度。为此本文设计了一种检测传感器的输出与安装力矩的相关性的测试方法来验证两种不同结构传感器的安装敏感性。具体试验方案如下：利用可调扭矩扳手,将M4安装螺钉连同待测传感器固定到上下测试板上,螺钉旋入传感器螺纹孔中的旋合长度大约是9 mm。依次设定扭矩扳手的力矩为0.5,2,3.5,5 N·m,然后将螺钉旋紧,每一次按照设定的扭矩拧紧后,将安装好上下板的传感器水平放置,记录传感器的空载输出。图3为不同拧紧力矩作用下传感器空载输出相对0.5 N·m拧紧时传感器空载输出的平均变化量。

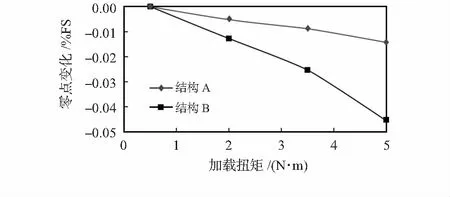
图3 二种结构传感器空载输出对拧紧力矩的敏感性

在拧紧传感器上测试板的螺钉或是下测试板的螺钉过程中,这两种结构传感器的零点输出都是逐渐减小的。从0.5 N·m拧紧到5 N·m的过程中,结构A和结构B分别产生了约-0.015 %FS和-0.045 %FS的零点漂移。从表3可以看出,结构B的应变片比结构A更靠近安装螺孔(约近10 mm),因此，安装敏感性大约增加了3倍。不过由于漂移量较小,这一零点漂移的影响因素还不足以影响测量精度。

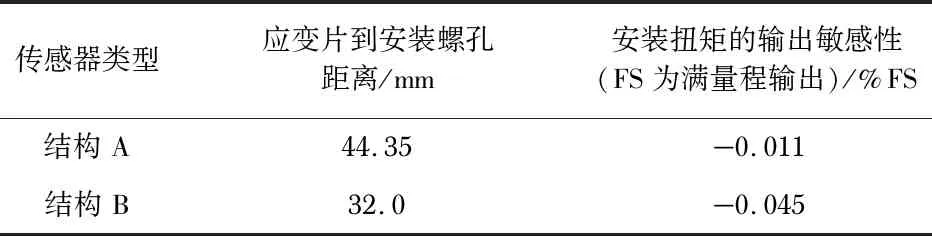
表3 安装扭矩与输出敏感性

2.3 弯曲刚度试验

使用5 N·m安装扭矩,将传感器安装好上下测试板后,水平放置,然后依次在上顶板的中心位置加载1,3,8 kg的砝码,同时用千分表测试上测试板产生的垂直变形量,结果如表4所示。

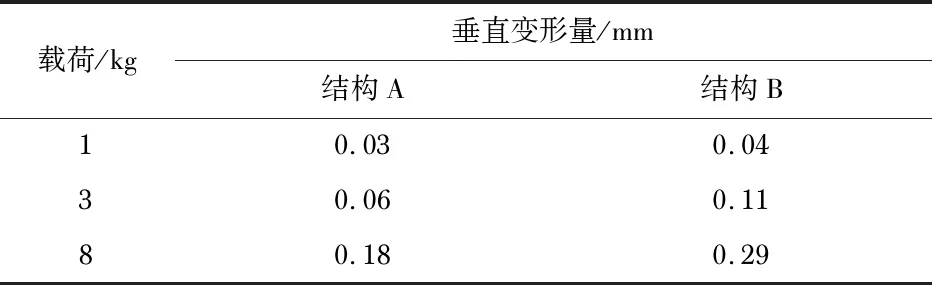
表4 挠度试验结果

采用式(1)计算线性相关的决定系数R2,结果表明:传感器的垂直位移变形量与所加载荷之间是线性关系(如图4所示)

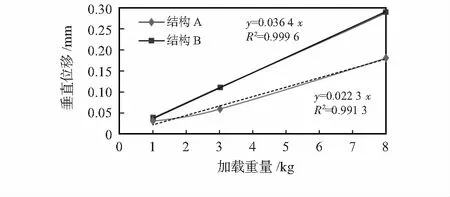
图4 二种结构传感器的挠度vs载荷

(1)

二种结构的弯曲刚度计算结果如下

结构 A:k=F/y=1/0.022 3 N/mm=44.84 N/mm；

结构 B:k=F/y=1/0.036 4 N/mm=27.47 N/mm。

计算结果表明,结构A的刚性比结构B要高63 %。

2.4 冲击动态响应试验

本文采用了一种类冲量式的测试方法来比较两种结构传感器的动态相关性能：首先将传感器安装到秤架中,然后将大约3 kg的沙袋作为重物从秤台正上方1 m处自由下落。试验过程中尽量保证重物落在秤台的中间位置,以避免附加的扭转变形与研究所关注的弯曲模态耦合。

图5为其中一只结构B传感器在3 kg沙袋掉落前后的数据变化情况：其空载输出在-0.3 V,大约在采样开始1.53 s左右,重物掉落到秤盘上,由于冲击产生的传感器输出信号过大,已经超出了采集仪的最高采集范围,采集仪输出了0.2 V的饱和电压,出现图中的第一个峰值A。在1.6～1.7 s时,由于重物被弹起,出现约0.1 s的空载区间,此时,可以看出传感器和秤台的振动波形,后续根据这个波形计算传感器空载时的响应频率。同时可以看出,由于冲击载荷过大,传感器此时的控制输出已经产生了一定的正向漂移。在1.7～1.8 s时,重物又落回到秤台上,所以，在1.8～1.9 s的区间,可以看到3 kg载荷作用在秤盘上时,传感器的振动波形。

图5 结构B传感器样品对冲击载荷的响应情况

根据图5中1.6～1.7 s区间的传感器空载振动波形数据和1.8～1.9 s区间的3 kg载荷作用下的传感器的振动波形,计算出传感器测量的响应频率,如表5所示。

表5 传感器响应频率测试数据 Hz

将传感器、秤盘和载荷简化为一个质量弹簧系统,然后根据式(2)计算得出试验中传感器系统的响应频率

(2)

式中m为包含传感器、秤盘和重物的系统总质量，k为前次试验中得到的弯矩刚度。根据式(2),计算得到的传感器系统响应频率和加载质量的关系如图6所示。

图6 二种结构传感器计算的响应频率

从图6可以看出,若在没有载荷和秤盘的情况下,结构A传感器的响应频率约在355 Hz,结构B传感器的响应频率约在291 Hz,与之前有限元分析结果(表1)基本一致。已知秤盘的质量约为600 g。相对应地,传感器在安装好秤盘后,结构A传感器的响应频率下降到128 Hz,结构B传感器的响应频率下降到101 Hz。并且随着载荷的不断加大,二种结构传感器的响应频率的降低趋势是一致的：在空载阶段,结构A的响应频率比结构B高约27 Hz；当满载到8 kg时,结构A的响应频率比结构B高约8 Hz。而从图7可以看出,表1计算的理论响应频率和表5中测量的响应频率之间基本体现了良好的一致性,尤其是结构B传感器其计算和测试响应频率基本一致。

图7 二种结构计算的响应频率和测量的响应频率差异

本文采用了将上升曲线和下降曲线延伸相交的方法来评估传感器可能的最大输出峰值,并使用如下定义：信号放大系数=传感器最大输出(3 kg传感器从1 m高处掉落)/传感器静态输出(3 kg载荷),由此得到表6数据。

表6 传感器信号放大系数比较

根据表6可知,一个3 kg的重物从1 m高处掉落到结构A传感器秤盘上,产生的信号相当于34.8 kg的重物静态加载在传感器上；同理,若同样情况掉落到结构B传感器秤盘上,产生的信号相当于31.2 kg的静态载荷作用在传感器上。结构A传感器对动态加载的信号放大系数比结构B高约10 %。

而图6中测试曲线后半部分表明,由于冲击载荷的作用,传感器的零点输出发生了正向漂移,统计结果如表7所示,说明结构A传感器受冲击产生的零点漂移比结构B高约35 %。

表7 传感器冲击载荷与零点漂移量 %FS

3 试验结果讨论

从计量性能试验结果,可以看出两种结构的传感器的静态性能基本一致,相关指标都可以满足计量要求,静态精度可以达到0.01 %FS左右,因此,在非动态测量场合,两者之间具有互换性。

在动态特性方面,在安装敏感性试验中，结构B传感器变化是结构A的3倍，文中认为,主要是因为结构A的应变片相对结构B距离安装区域更远,按照圣维南定理,安装区域产生的局部应力就不容易影响到更远的目标,故结构A可以更好地减少安装基座振动扭曲带来的附加应力影响。在弯曲刚度试验中,结构A传感器的刚度比结构B高约63 %,同时,在任意载荷下计算的响应频率都比结构B要高,试验中在只有台面重量(600 g)和3 kg加载情况下测量得到响应频率与上述计算结果基本一致。有限元计算显示,保持传感器容量不变的情况下,减小双孔间距,传感器的刚度和响应频率都相应提高。因此,主要是由于结构A的双孔间距更小,故其刚度和响应频率都更好。而在冲击动态响应试验中,结构A传感器得益于更好的刚度,试验结果显示其对冲击信号的放大效果要比结构B高约10 %,这一点对于测量非常有益,可以帮助提高传感器输出信号的信噪比。但试验数据也表明结构A传感器更容易受冲击载荷作用发生零点漂移。

4 结 论

双孔平行梁式谷物流量传感器的孔间距尺寸是影响传感器动态性能的一个关键参数：随着孔间距的减小,传感器的动态响应提高,同时传感器信噪比也更好。实验中,二种结构传感器的静态性能基本相同,但是结构A由于孔间距更小,其相对结构B具有较好的动态特性,因此，被认为更适合作为冲量式谷物流量测量传感器使用,但需要考虑谷物的最大冲量大小与传感器的动态放大系数和容量相匹配,有待进一步试验研究。