基于无人机控制和最优视图视选择的动作捕捉方法*

孙 冬

(河南工学院 计算机科学与技术学院，河南 新乡 453003)

0 引 言

3D人体姿态捕捉与识别[1]的发展越来越成熟，其在步态识别、视频监控、人机交互等领域有着重要应用，是当前热门研究课题。虽然3D人体动作姿态捕捉的性能得到显著改善，但准确度依然较低。如何提高3D动作姿态的性能，不仅要从算法角度提高，还需要从视点选择方面入手。

当前大部分无标记运动捕捉方法依赖于单目图像回归的深度网络[2]，在多视角设定下，运动捕捉的最优相机位置的问题尤为关键[3]。当前主要解决方案包括最大化图像分辨率，人体部位自遮挡[4]，三角测量误差最小化[5]。但这些方法的缺点是必须离线操作，且针对预先记录的动作。

针对静态人体动作姿态的视图规划，很多研究在最小化运动成本的前提下通过相机的移动来最大化信息增益，如文献[6]利用高斯过程回归解决输入输出均为多元变量的人体姿态估计问题，采用稀疏表示法降低计算复杂度。文献[7]将空间离散化为立体网格并计算先前体素。但这些方法的缺点是必须针对严格不变的场景。文献[8]在获得粗略场景模型的情况下，通过离线优化得到最优轨迹。但这些方法的缺点是必须针对严格不变的场景。

通过无人机(unmanned aerial vehicle，UAV)相机捕捉人类运动的研究中，一个重要的问题是UAV必须将目标人物保持在其视场内。为此，文献[9]实施了一个预定义的随机决策，相机与目标保持恒定距离，并利用预定义视角来最大化三角测量准确度。但依赖于标记进行准确的2D姿态估计。文献[10]UAV采用恒定角度飞行，通过最大限度降低3D人体关节位置的不确定性来优化相机移动轨迹，但该方法的3D姿态估计必须离线执行。总之，当前方法或者针对刚性场景优化UAV位置，或者在不优化相机放置位置的情况下估计3D人体姿态，其均未尝试利用对相机的主动控制来提高准确度。

本文提出利用后验方差估计值，将不确定性来源(行为的不确定性、姿态估计法的可靠度等)与先验分布相融合，开发出主动运动捕捉技术，取移动相机的原始视频片段作为输入，针对人体运动捕捉优化，计算出用于相机定位的最优视点。合成和现实视频片段的仿真证明了所提方法能够提高估计的准确度。

1 提出的动作捕捉方法

1.1 总体框架

本文提出的方法框架如图1所示，主要包括以下3个步骤：1)估计至当前时刻的3D姿态；2)预测当相机获得下一张图像时的人物未来位置和3D姿态，其中包括不确定性估计；3)基于不确定性估计选择最优相机姿态，并将UAV相机移动至该视点。

图1 本文捕捉人体运动的框架图

本文考虑两种相机移动方式：1)相机可不受限制地从一个位置传送到另一个位置，以此来探索本文方法的理论极限。可利用多相机设置来模拟该传送模式，从而可以在模拟数据以及从多个视点获得的真实图像数据集上评估本文模型。2)通过一个模拟UAV来携带相机，其运动必须遵循物理约束。

1.2 3D姿态估计

3D姿态估计步骤将机载相机过去N帧的视频作为输入，并针对每帧t∈(1,…,N)输出表示为15个3D点Wt∈R15×3的3D人体姿态，以及表示为3D位置和旋转角度Dt∈R2×3的UAV姿态。在估计3D人体姿态时，首先利用文献[10]提出的方法检测图像平面中人体主要关节的2D位置Mt∈R15×2，然后，将2D预测提升到3D姿态Lt∈R15×3。但由此得到的每帧输入容易出现误差，为此，本文在空间—时间优化中将2D和3D预测与时间平滑性和骨骼长度约束相融合。由于UAV在不断移动，因此可消除个体估计歧义。针对每个目标执行一次校准，在该阶段中计算出目标骨架的骨骼长度bl，该阶段中目标必须保持20 s的静止站立姿态。

1.2.1 参数定义

本文的目标在于提高对变换位置和姿态目标的全局3D人体姿态估计准确度。所提方法对最后k帧的时变姿态估计进行优化。设t为最后一个观察到的图像帧。捕捉姿态矩阵W中从姿态Wt-k到Wt的轨迹。能量函数表示为

Epose=Eproj(W,M,D)+Elift(W,L)+Esmooth(W)

+Ebone(W,b)

(1)

式中 升维项Elift利用LiftNet[11]的3D姿态估计L。由于该方法与人体臀部相关，且没有绝对比例，因此,从绝对3D姿态Wt中舍去臀部位置，并将比例因子m应用到L，从而在最小二乘意义上匹配骨骼长度bl，由此得到

(2)

式中ωl为相对高度；Whip为踝关节姿态。

投影项Eproj表示在最小二乘意义上，检测到的2D关节位置和估计出的3D姿态投影差异，其具体表示为

(3)

式中 ∏为透视投影函数，K为相机内部参数矩阵，wp为Eproj的影响控制权重。

由于本文使用连续视频片段，且运动是平滑的，平滑项Esmooth对通过有限差分计算出的速度进行惩罚

(4)

式中ws为Esmooth的权重。

(5)

式中wb为Ebone的权重。

1.2.2 校准模式

针对每个目标仅需执行一次校准模式，以得到骨骼长度bl。该模式中，假定目标是静止的。这种情况类似于从多个静止相机中观察到的场景。找到能够对下式最小化的单个静止姿态Wc

Ecalib=Eproj(Wc,M,D)+Esym(Wc)

(6)

该目标函数中，Eproj作用于所有校准帧，可表示为

(7)

式中wp为影响控制权重。对称项Esym确保了估计出的骨架左侧和右侧肢体有着相同长度。

1.3 下一个最优视图的选择

特征值之和捕捉多变量分布的扩散。为利用该不确定性估计，本文对Epose进行扩展，使其以过去姿态、当前姿态，以及未来的UAV位置选择为条件，对未来姿态进行建模。为了确定下一个最优UAV姿态，对候选位置进行采样，并选择有着最低不确定性的位置，如图2所示。图2(a)为3D椭圆体视图，图2(b)为2D俯视图。每个椭圆给出了臀部位置的特征值。此处，上一张图片从顶部(位置16)拍摄，并通过移动至正交视图的方式来最小化不确定性。

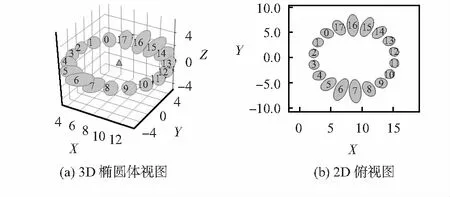
图2 候选UAV位置的不确定性估计

(8)

投影项Eproj从图像平面方向缩小了解空间，但并不约束深度方向，由此创建出椭圆的不确定性，如图2所示。

3)方差估计。投影项和先验项使得Epose及其相应的后验项有着复杂的形式。因此，方差Σp无法以闭合形式表达，且通过对所有可能姿态的空间进行采样对其逼近的成本很高。因此，本文利用高斯分布q对p(W|M,D,L,b)进行局部逼近，使得

Σp(W|M,D,L,b)≈Σq

(9)

式中q=N(W|,Σq),和Σq分别为高斯均值和方差矩阵。对于一个高斯函数，可以通过闭合形式计算出q的协方差，即：负对数似然的海森矩阵的逆，在高斯假设下，通过Epose的二阶梯度能够很好地逼近Σp。

为了在包含K个候选UAV轨迹的集合中选择有着最小不确定性的视图，需进行以下4个步骤：步骤1:对于1≤i≤M，对Epose进行一次优化，以预测M个人体姿态t+i；步骤2:对于每个候选估计c，利用这些预测姿态，为每个1≤i≤M设定t+i和t+i；步骤3:对于每个c，计算Epose的二阶梯度形式；步骤4:计算特征值并进行求和，以选择具有最小不确定性的候选集。

1.4 UAV控制策略与飞行模型

在UAV模拟飞行实验中，本文在9个候选轨迹之间作决策，轨迹方向有：上、下、左、右、右上、左上、右下、左下和中。为确保UAV与人体之间保持固定距离，通过固定距离值对方向向量进行归一化。

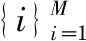
xpo=xcu+vcuΔt+0.5acuΔt2

(10)

时间t时的当前加速度为输入加速度ain和上一个时间步的加速度apr的加权均值为

acu=βain+(1-β)apr

(11)

基于要评估的候选轨迹来确定ain的数值，系数β通过行搜索得出。在实际操作中，将加速度向量的方向设为候选轨迹的方向。通过预测xpo和实际UAV位置之差的最小二乘最小化，来确定输入加速度的大小。通过预测UAV的未来位置，可以得到更准确地进行2D姿态估计，从而提高决策的准确度。

2 实验与结果分析

2.1 仿真设置

1)仿真环境：为了提高仿真的实践意义，本文使用真实运动捕捉数据，以及建立在游戏引擎上的AirSim UAV模拟器，提供接近现实的自然环境实验情形。使用模拟器的另一个好处是可以利用不同参数重复相同的实验，并与基准方法和真实运动情况作比较。

2)CMU数据集[14]：模拟测试在CMU数据集上进行，该数据集包括多个复杂动作，如跑、跳舞、等动作。本文在难度递增的三个CMU运动上进行测试：直线行走(目标2，实验1)；旋转跳舞(目标5，实验8)；以及绕圈跑(目标38，实验3)。此外，本文还使用了篮球运球(目标6，实验13)和坐凳子(目标13，实验6)的验证集，进行超参数网格搜索。

3)MPI—INF—3DHP数据集[15]：为检测所提方法在模拟器之外的性能，实验在MPI—INF—3DHP数据集(3D人体姿态识别数据集)上进行评估，该数据集包含绕圈跑、挥舞手臂等动作，提供了14个固定视点，且这些视点彼此之间与目标间均有着不同距离，如图3所示。

图3 MPI—INF—3DHP数据集与固定视点

4)对比的基准方法：当前基于UAV的姿态估计方法利用预定义的策略来控制相对于人体的UAV位置。其中UAV以恒定角度跟踪人体，或者UAV围绕人体不停飞行。本文选择随机决策方法[9]作为一个基线策略，同时比较了恒定角度环绕飞行方法[10]；然后，通过对下一个时间帧的图像进行所有视点的穷举尝试，并将UAV移动至在下一个时间步中最小平均误差的视点，由于该场景中无法控制相机，移除了在视点外的候选位置相机。

5)超参数：通过网格搜索，将重建的损失项权重设定如下：wp=0.000 1，ws=1，wl=0.1，wb=1。将决策制定的权重设为wp=0.001，ws=1，wl=0.1，wb=1。

2.2 结果与分析

实验首先进行初始化，通过第一帧中的2D关节位置估计Mt=0，进行反向投射初始化。然后，通过不带平滑项的优化对该初始化进行细化，对所有序列进行120帧的评估，动画序列以5 Hz播放。此外，对于传送模式，时间窗口大小设为k=2个过去帧和1个未来帧；对于UAV飞行模拟，时间窗口设为k=6个过去帧和3个未来帧。

2.2.1 传送模式

为分析潜在视点的不确定性估计是否与实际3D姿态误差相吻合，本文进行以下模拟：在人体周围环形中采样18个点，并支持无人机传送到这些点中的任意一点，实验中，共计优化k=2个过去帧，并预测未来1帧图像。

第1个实验，将高斯噪声添加到真实数据集中，模拟2D和3D姿态估计。该噪声的平均和标准偏差设为数据集上运行的误差。表1给出了该实验的结果，包含不同动作姿态、从不同视点开始、有着不同噪声情况的结果。

表1 传送实验中的3D姿态准确度

第2个实验在没有噪声的MPI—INF—3DHP数据集上进行。图4给出了通过本文方法和基准方法所生成的轨迹。由图4可知，与基准方法相比，本文的主动运动规划方法的误差值较低，且最接近这些序列和视点的最优可能误差性能。由于本文方法利用了UAV可传送到不同的视点集合，因此在实验中体现出良好的性能。

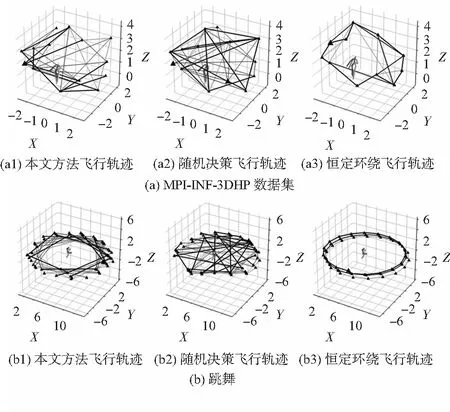
图4 传送模式下几种方法的飞行轨迹

2.2.2 UAV飞行模拟

为评估更具现实性的案例，对UAV进行主动控制，且约束其只能移至附近位置，实验利用AirSim环境模拟UAV飞行。在该仿真中，指定了目标周围7 m的固定半径区域，提供了能够保持该距离的方向候选，还约束UAV在0.25～3.5 m的高度范围内飞行，以避免坠落地面。

实验使用模拟器模拟无人机飞行。对上、下、左、右、右上、左上、右下、左下和中心这9个候选方向进行采样。然后，使用简化(闭合形式)物理模型预测3个连续未来位置，对UAV沿某个方向飞行时的位置进行估计。最后，估计这些样本视点的不确定性，并选择不确定性最小的视点。

图5给出了所提方法和不同基线方法的轨迹。由于UAV动力限制，随机基线方法不能在其相机视点之间增加距离。由图5可知，所提方法与持续环绕方法的性能大致相当。除了无人机开始飞行的前几帧之外，本文方法与持续环绕的轨迹是相同的，仅环绕方向上有差异。这是由于持续环绕方法有利于保留动量。因此，本文方法支持UAV在保持目标在视图中的前提下，可以对较远的视点进行采样。

图5 UAV飞行模式下几种方法的飞行轨迹

3 结 论

本文提出一个利用无人机控制和视点最优选择进行不确定性估计，完成人体动作姿态捕捉。通过最优视点选择，将视点移至最低预期不确定性的位置，从而提高3D人体动作姿态估计性能。实验结果表明:在不受物理约束的情况下选择下一个视点时，所提方法性能优于基线方法(例如围绕对象不停环绕，或与对象保持恒定角度)。对于模拟UAV飞行，所提方法与不停环绕方法性能大致相当。

虽然所提方法使不确定性估计可跟踪，但未来本文还需要作进一步研究。例如，分析一些深度学习方法的参数不确定性估计，优化无人机飞行轨迹等。