小样本下基于卷积神经网络的费用估算研究

刘鑫容，朱耀琴，曲慧杨，周军华

(1.南京理工大学计算机科学与工程学院，江苏 南京 210094； 2.复杂产品智能制造系统技术国家重点实验室，北京电子工程总体研究所，北京 100854)

0 引言

近几年来，随着导弹研制技术和社会经济的发展，导弹的研制费用也逐渐增加，如何平衡导弹研制的需求和研制过程产生的费用之间的关系，成为了一个至关重要的研究热点.要解决这个关键问题，需要一个可靠且稳定的估算方法进行费用估算，为研制出符合精度和费用要求的导弹提供参考.

近几十年来，我国不断在费用估算方面进行研究与探索，经历了一系列的方法革新.传统的费用估算方法包括工程估算法、参数估算法、类比估算法，这几种方法在早期有较多的应用，例如文献[1]利用了工程估算法，对装备再制造费用进行分解，提出了再制造费用的估算方案；文献[2]则类比Burns模型对建立了一种三代战斗机改进型的出厂费用估算模型，改善了计算精度.

上述方法多为线性方法，拥有一定的预测能力，但是无法模拟出更加复杂的产品参数关系.而此后涌现的灰色系统理论侧重于分析一些不完全确定的系统，能够应用于费用估算.在文献[3]中采用了灰色系统理论对装备费用进行估算，构建GM(1，1)模型和GM(1，1)预测模型，以实际样本证明该方法的估算效果；而神经网络通过学习样本属性和费用之间的关系估算费用，根据RBF神经网络理论建立了一种分析模型[4]，用于分析大型客机的制造成本，证明了该模型能够得到较精确的结果.

然而，灰色系统理论和神经网络也存在局限性，二者较依赖数学模型，无法结合实际样本对模型参数进行大幅度调整.而卷积神经网络(Convolutional Neural Network，CNN)可学习样本特征并提取其中的内在联系，可以根据损失调整模型结构，具有较强的适用性，能够应用于估算领域，提高预测精度.

卷积神经网络早在2006年之前就已被提出，直至2012年，在ImageNet大规模视觉识别挑战竞赛(ImageNet Large Scale Visual Recognition Challenge，LSVRC)中，利用深度的卷积神经网络取得了当时最佳的分类效果[5]，鼓励了学者投入卷积神经网络的研究.

而在估算预测领域也早有学者构建卷积神经网络对各种参数进行学习预测，例如文献[6]利用卷积神经网络预测沪锌期货的价格，利用对比实验证明该模型具有良好的预测效果；文献[7]构建卷积神经网络模型，预测搜索广告的点击率，验证了该模型的预测精度较高.

由于导弹结构复杂，导弹研制过程存在特殊性，导弹的特征属性和研制费用往往难以获取，公开的样本十分有限，且各个导弹样本之间存在型号和性能上的联系，不同的样本对待预测样本的参考意义不同.故在该条件下，本文采用了双三次插值法与反距离加权插值法结合，对样本进行扩充.结合卷积神经网络构建导弹研制费用的卷积神经网络估算模型，验证了该模型的估算能力.

1 小样本下基于卷积神经网络的导弹研制费用估算模型

1.1 模型流程

在小样本条件下，本文采用双三次插值法以解决导弹的原始样本集数量有限的问题，采用反距离加权插值法以解决样本贡献值问题，利用两种插值算法扩充导弹研制费用原始样本后，输入卷积神经网络模型中预测估算.小样本下基于卷积神经网络的导弹研制费用估算流程见图1.

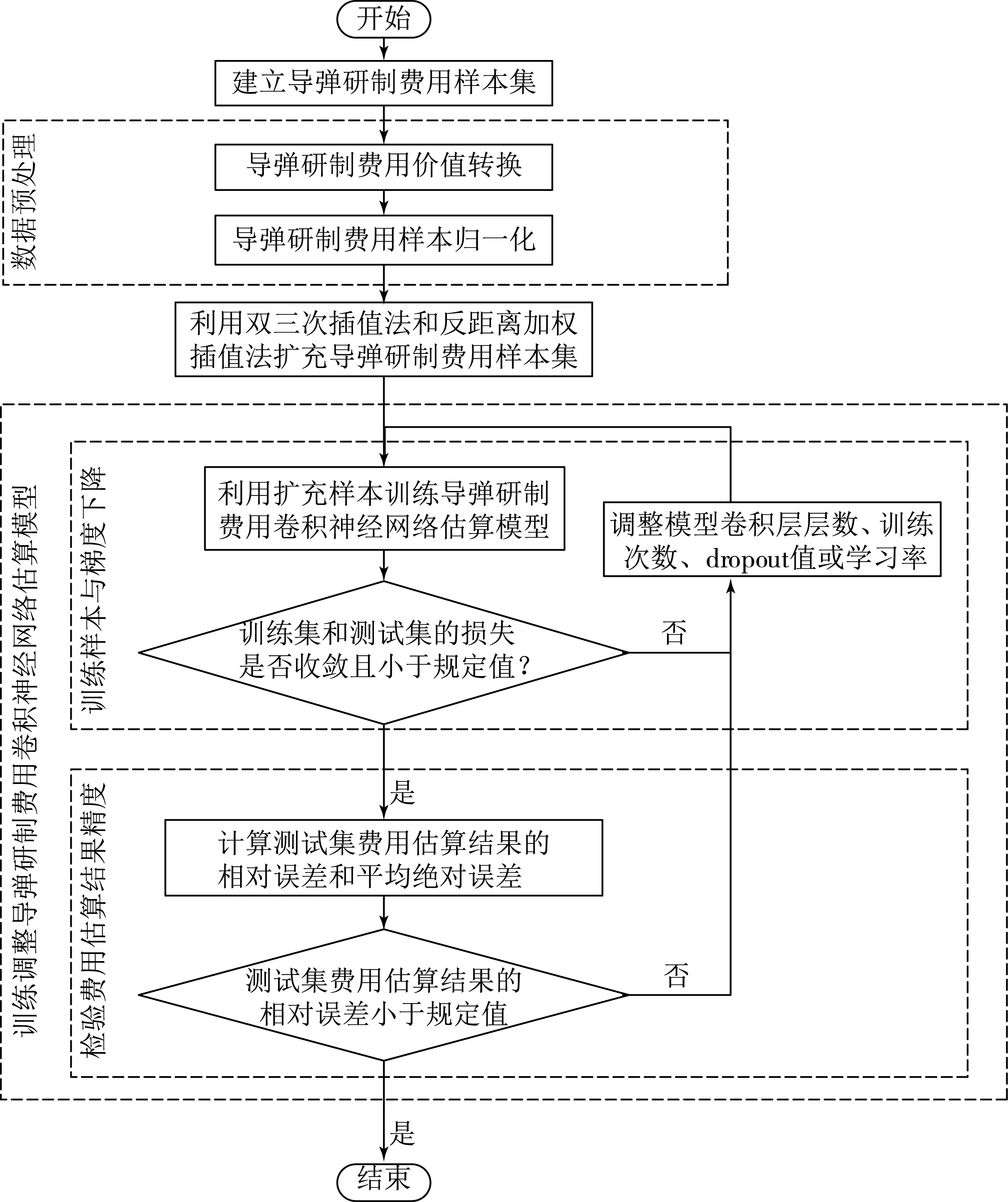
图1 小样本下基于卷积神经网络的导弹研制费用估算流程

步骤1 导弹研制费用样本集的建立.

导弹研制费用样本集是从原始的导弹数据库中获取导弹的特征属性和研制费用样本，参照已有的研究成果，选取了对导弹研制费用具有关联影响的导弹特征属性，例如导弹的最大射程决定了导弹杀伤目标的最大距离[8]，故射程增大，对导弹的性能要求增大，则必然导致研制费用的增加.通过选取影响导弹研制费用的性能及相关属性，能够增强模型的泛化能力和学习的鲁棒性，有助于模型对样本集的学习和估算.

步骤2 数据预处理.

(1) 研制费用价值转换.建立样本集后，需要对导弹研制费用样本集的特征进行一定的分析，处理各属性之间关系.考虑到通货膨胀的情况，不同的时期下，相同价格的研制费用在价值上也不尽相同.为了平等地对比各个导弹样本的研制费用，应当将各个样本的研制费用转换成相同时期下的同等币制.利用居民消费价格指数(consumer price index，CPI)，根据文献[9]中费用转化公式可将导弹研制费用转换到同一财年.

(2) 导弹特征属性归一化.由于导弹的各个结构属性决定导弹的研制费用，数值差异较大，若未处理，容易被数值大的导弹属性所主导.为了更好地体现各个导弹特征属性之间的关系，减少训练过程中的计算量，将采用文献[10]中提到的归一化方法对导弹特征属性进行归一化处理，使其取值在[0，1]之间，缩小导弹特征属性差异，避免模型参数波动大.

步骤3 基于双三次插值和反距离加权插值的样本扩充.

由于导弹的公开样本数目有限且各个样本对于待预测样本的贡献值不同，如何解决上述问题成为本文研究的关键，是原始样本集处理的重要环节.本文对原始导弹研制费用样本进行双三次插值，对与待预测样本型号性能相似的若干原始样本通过反距离加权插值法进行插值.

步骤4 训练调整导弹研制费用卷积神经网络估算模型.

(1) 训练样本与梯度下降.以导弹研制费用的扩充样本作为输入，建立导弹研制费用的卷积神经网络估算模型.训练卷积神经网络模型，通过均方误差计算训练集和测试集的损失，观察二者关系及是否收敛，判断模型是否欠拟合或者过拟合.通过不断对模型的卷积层层数、训练次数、dropout值或学习率进行调整修改，以达到损失收敛且较低的状态.

(2) 检验费用估算结果精度.计算测试集样本的评价指标以检验该模型的估算精度.若计算结果符合精度要求，则该卷积神经网络模型可用于导弹研制费用的估算，否则，则回到上一步重新进行训练.

1.2 基于双三次插值和反距离加权插值的样本扩充

为了取得导弹研制费用的良好估算效果，原始导弹研制费用样本集存在以下两个问题：(1)获取导弹的特征属性和研制费用存在一定困难，可用的公开样本数目少；(2)各个导弹样本之间存在型号和性能上的联系，不同的样本对待预测样本的参考意义不同.本文为解决上述问题，从小样本和样本贡献值两个角度出发，采用双三次插值和反距离加权插值两种插值方法对样本进行扩充.

在小样本条件下，目前有两种研究方法：一是利用先验条件建立预测模型，但此方法对先验条件的要求较高，因此应用场景较少[11]；二是样本扩充法，本文利用当下应用广泛的解决方案处理小样本问题.

针对导弹型号属性相近的样本，对研制费用的估算也更具有参考意义的特点，反距离加权插值采用了相似相近的原则，型号相近的样本对插值具有更高的权重，可用于处理样本贡献率问题.

本文结合双三次插值和反距离加权插值，针对原始导弹研制费用样本进行双三次插值，通过反距离加权插值法对与待预测样本型号性能相似的若干原始样本进行插值.这种方法既使得能够有效扩充样本容量，使样本分布于导弹研制费用原始样本集中，具有一定的规律性和广泛性，又能在待预测样本附近拟合出更多样本，达到对相似样本加权的目的.

1.2.1 双三次插值法扩充样本

双三次插值法用于将原始导弹研制费用样本扩充成若干有序样本，插值样本分布于各原始样本之间.导弹研制费用属性Y和导弹特征属性为X=(x1，x2，x3)的3条原始样本在k=2时的插值流程见图2，样本在经历两次插值得到新的导弹研制费用和特征属性插值点后，筛选出包含(Y，x1，x2，x3)的插值样本，得到最终的扩充样本.

针对单一导弹插值点，如图2的局部放大图所示，双三次插值法利用了插值点附近的4个方向上的16个原始导弹样本点进行加权插值，既考虑了4个相邻点的数值影响，也考虑了各相邻点数值变化率的影响[12].

图2 双三次插值法扩充样本图示(k=2)

具体的操作流程：

步骤1 设置插值的优化因子k；

步骤2 在每一个维度上的间隔之间对网格数组形式的原始导弹研制费用样本都进行切割，形成优化的网格数组；

步骤3 在网格之间插入数值，反复切割k次，生成2k-1个插入点；

步骤4 保留插值网格的纵列中包含原始属性(Y，x1，x2，x3)的列，得到导弹研制费用样本的扩充样本集.

图3 双三次插值法扩充样本流程

双三次插值法扩充样本流程见图3.

1.2.2 反距离加权插值法扩充样本

考虑到不同型号和性能的样本对待预测样本估算的贡献率不同，本文采用反距离加权插值法对相似样本(即与待预测样本型号性能相似的若干原始样本)进行插值，以达到增加其数量及加权的目的.

由于反距离加权插值利用相似相近原理进行插值，通过相似函数计算得到的相似样本的距离也会越近，与插值点越相似，使得拟合得到的估算值也会越贴近相似样本.

具体的插值流程：

步骤1 导弹特征属性为(ai，bi，…，ni)的原始导弹样本的相似函数为

其中hi是当前导弹研制费用样本到插值点的距离，(ai，bi，…，ni)为导弹样本的各个特征属性，个数由导弹特征属性个数决定.

步骤2 根据随机抽取正态分布规律中概率在(μ-2σ，μ+2σ)范围内的一组概率α.

步骤3 根据正态分布规律在相似样本的属性值附近建立正态分布模型，其中均值和标准差由当前相似样本的导弹特征属性值决定.

步骤4 根据概率α求出导弹特征属性插值点(a，b，…，n)，插值点的每个属性xα服从P{X≥xα}=α，同一组插值点概率α相同.

步骤5 根据反距离插值法的公式，输入导弹特征属性随机插值点(a，b，…，n)拟合得出对应的导弹研制费用为

步骤6 将拟合结果和导弹特征属性整合，得到若干相似样本附近的插值样本.

反距离加权插值法扩充样本流程见图4.

图4 反距离加权插值法扩充样本流程

1.3 导弹研制费用的卷积神经网络估算模型

由于卷积神经网络具有更深度地学习能力，可以根据导弹研制费用原始样本提取各个属性之间的关联，参考损失值和费用估算的结果及时调整模型的结构和参数，应用于导弹研制费用的估算.图5是导弹研制费用的卷积神经网络估算模型.

图5 导弹研制费用的卷积神经网络估算模型

模型主要的功能层及实现策略：

(1) 输入层.经过扩充后的导弹研制费用样本集通过读取文件的模式读入，对导弹特征属性进行归一化处理，便于之后的卷积计算.根据读入的样本构建导弹特征属性方形矩阵，作为二维卷积的输入.

(2) 卷积层.由于本文中输入的数据较小，故仅使用卷积操作对导弹研制费用样本集进行特征提取，卷积操作能够增强原样本的特征属性.

由于卷积核的尺寸越大，能够得到更多参数，但模型的学习速度也会减缓；卷积核的数目越多，能够得到更多的描述特征，但计算量也会相应增加，所以应当选择合适的卷积核大小及数目，以得到良好的学习估算效果.

本文根据模型输入数据的大小，选择卷积核大小为2×2，步长为1的卷积核，经过4次卷积作用及激活函数Relu函数的激励，得到卷积后的特征.

(3) 全连接层.搭建在整个网络的尾部，能够将经过卷积后的特征与输出层相连，减少特征信息的损失.全连接层组合的特征加以Relu函数的激活，送入dropout层.

(4) dropout层.使得每一层的神经元都部分失活，防止模型产生过拟合，避免模型由于过度学习大数据的冗余信息，导致训练速度慢，缺少泛化能力.

(5) 输出层.将均方误差作为损失函数，计算后用Adam优化器进行优化，经过数次梯度下降，得到导弹研制费用估算结果.

由于导弹研制费用的卷积神经网络模型可以得到唯一输出的研制费用估算值，故采用回归模型的评价指标对模型进行评估并改进：采用均方误差(Mean Square Error，MSE)作为模型的损失函数；针对费用预测估算的结果，采用平均绝对误差(Mean Absolute Error，MAE)和相对误差(Relative Error)，评估模型对样本整体和个体的估算准确度.

2 模型实现与比较分析

2.1 实验方法

实验在Win10操作系统下，利用MatlabR2016a编程实现导弹研制费用原始样本集的扩充，在Pycharm下利用Tensorflow框架对导弹研制费用的卷积神经网络估算模型进行训练，开发语言为Python3.6.

实验利用Matlab实现对原始样本集的扩充，原始样本集为8组导弹研制费用样本集，包括导弹特征属性及其研制费用.将8组样本分为7组训练样本和1组待预测样本，分别根据双三次插值及反距离加权插值算法对原始导弹研制费用训练样本扩充到300组数据.

扩充样本经过数据预处理，采用1.3节提出的导弹研制费用的卷积神经网络估算模型，根据参数调节结果，选择卷积层层数为4，学习率0.01，反复迭代训练5 000次.为了验证研制费用估算结果的优略，采用均方误差作为损失函数进行梯度下降，平均绝对误差和相对误差分别判断测试样本的整体和个体的估算准确度，根据评价指标不断优化模型，得到最优模型.

2.2 参数调节

在实际模型训练的过程中，估算效果好的模型需要在训练的过程中不断调节参数、调整模型的结构，参考模型评价的指标才能最终得到.本文选取卷积层层数、dropout值、学习率3个参数对卷积神经网络模型的估算精度进行评估分析.

在实验操作中，设置卷积层层数为4，学习率为0.01，dropout值为0.5，训练次数为5 000次，使用控制变量方法，单次实验只改变卷积层层数、dropout值、学习率三者之一，得到待调整参数与测试集的MAE的关系见图6—8.

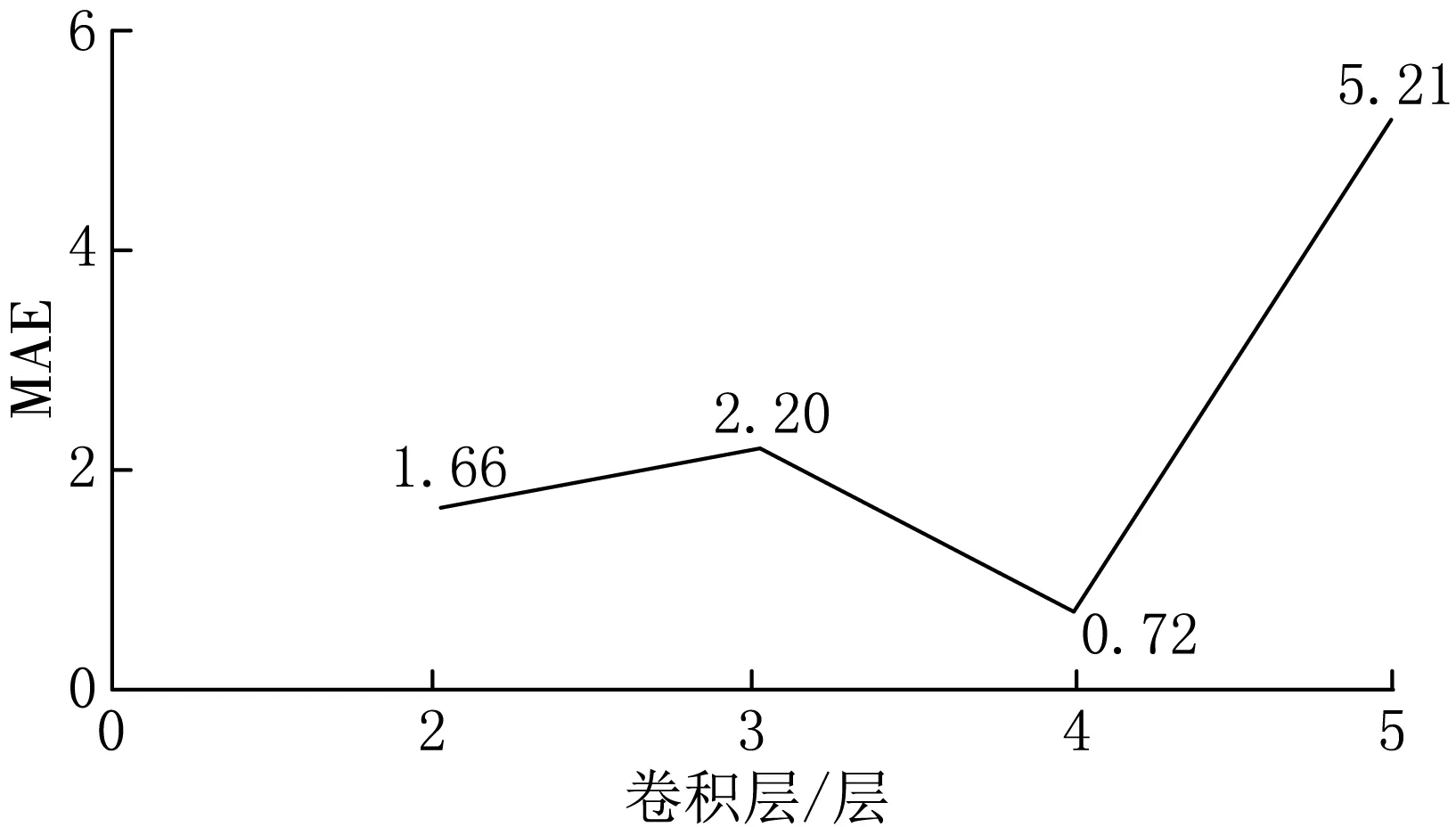
图6 卷积层层数与MAE的关系

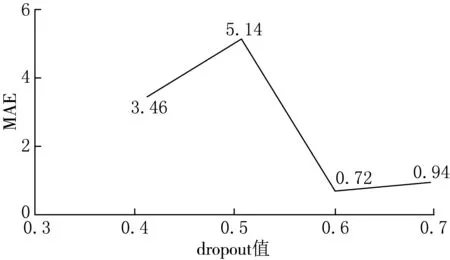
图7 dropout值与MAE的关系

图8 学习率与MAE的关系

从图6—8中平均绝对误差与卷积层层数、dropout值、学习率的关系图可以看出，在卷积层层数为4时，MAE达到最低值，整体的估算效果较好，可以得到较为准确的估算值.当dropout值等于0.6时，平均绝对误差达到最低值，此时dropout发挥出最佳的抑制过拟合效果，使模型具有泛化能力且能保证估算精度.当学习率为0.01和0.005时，模型的拟合效果明显，能得到较低的平均相对误差.由于学习率为0.005时，需要更久训练的次数才能取得最佳的估算结果，故选择学习率为0.01较为合适.

2.3 实验验证

实验验证的样本集为8组导弹研制费用样本[8]，采用卷积神经网络模型对研制费用进行估算.实验中的导弹特征属性包括最大射程、最大射高、最大射速、导弹质量等，具体的数值见表1，将8组样本分为7组训练样本和1组待预测样本(导弹研制费用均换算到1992年的价格).

表1 研制费用原始样本

2.4 实验结果

本文模型估算出的费用结果与线性回归、神经网络、支持向量机、WPCA&WSVR几种实验方法进行了对比[9]，结果见表2.

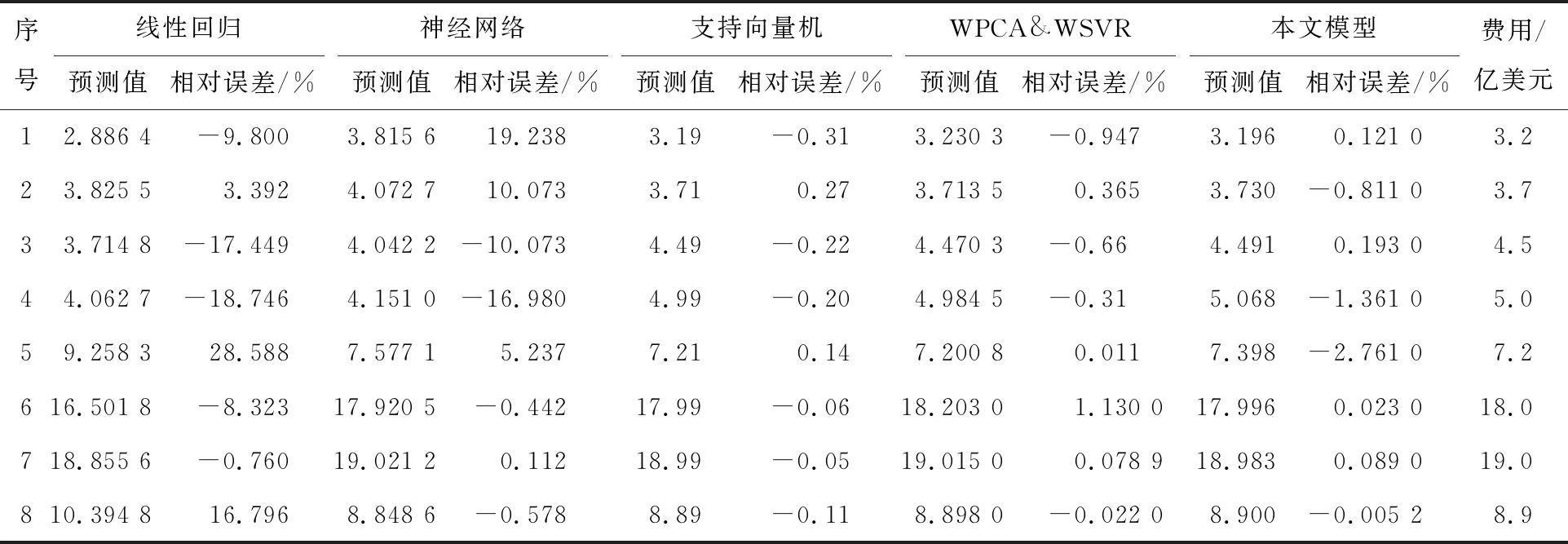
表2 本文模型与其他实验方法估算结果对比

从表2可以看出，本文模型在整体和待预测样本的估算结果都比线性回归、神经网络好.本文模型结合样本扩充，既能解决小样本和样本贡献率的问题，又能较好地学习各参数之间的复杂关系，对新样本的适应性较强，能够得到合理的估算结果，本文模型解决了线性形式无法表现复杂参数关系和在小样本条件下无法体现的泛化能力；与支持向量机和WPCA&WSVR费用两种方法相比，本文模型也在整体估算效果上优于二者，在待预测样本上的估算也明显优于支持向量机.

3 结语

本文针对小样本条件下的导弹研制费用估算问题，利用双三次插值和反距离加权插值进行样本扩充，解决了原始导弹研制费用样本数目稀少和各个样本对待预测样本的贡献值不同的问题.利用卷积神经网络可经过多次学习提取样本数据关联，调整模型结构的特点，采用导弹研制费用的卷积神经网络估算模型对扩充样本进行学习，对比验证了该模型的估算能力.然而，实验过程也存在一定不足，例如，调参过程繁琐且耗时长，需要花费较多的时间和人力，以后在这方面将进行探究.

致谢：对南京理工大学计算机学院提供的良好实验环境，教研组江涛同学、雷阳同学在实验模型构建和数据集收集的建议和帮助致以衷心的感谢！