基于伪柯西类核函数的主成分降维方法
2021-10-15刘文博梁盛楠
刘文博,梁盛楠
(1.黔南民族师范学院数学与统计学院,贵州 都匀 558000; 2.黔南民族师范学院复杂系统与智能优化实验室,贵州 都匀 558000)
0 引言
目前,诸多领域的数据呈现出高维度特点,即数据集包含几百甚至几千个变量,往往这些变量之间存在高度相关性且有些变量甚至与决策不相关.随着变量数目的增加,更会产生所谓的“维数灾难”[1],若直接利用机器学习算法进行处理势必大量增加时间开销.对高维数据进行降维、有效去除数据的冗余特征、降低特征之间的相关性是十分必要的.变量降维方法在基因表达数据识别[2]、图像聚类[3]、机器学习[4-5]等领域起到了数据预处理的关键作用.
降维技术主要分为特征选择[6]与特征提取[7].本文主要从特征提取的角度对高维基因表达数据进行维度约减研究,提高样本类别的识别率.特征提取的典型代表为主成分分析法(Principal Component Analysis,PCA),其基本思想是利用较少的主成分(综合变量)来替代原来较多的特征,而这些主成分能够尽可能多地包含原始特征的信息,并且彼此不相关[8],PCA擅长处理线性、高斯型分布数据.但是,在很多情况下,数据往往呈现出非线性分布,若仍采用线性降维,则将丢失原本的低维结构.因此,一些非线性降维技术应运而生,其中最为典型的代表就是基于核技巧的非线性特征提取方法.如Scholkopf等[9]提出的基于核主成分分析(Kernel Principal Component Analysis,KPCA),该方法通过非线性映射将低维空间中线性不可分的数据映射到高维空间,实现高维空间中的线性可分.
核主成分分析的关键之处在于核函数的选择,好的核函数可以更好地实现高维空间中样本的线性可分.鉴于此,本文构造了一类新的核函数——伪柯西类核函数,对高维数据进行降维.通过在4个癌症基因表达数据集的实验分析,与全变量、高斯核、多项式核、双曲正切核相比,在多数情况下,伪柯西类核函数的降维效果要优于传统的核函数以及全变量情形.
1 核主成分分析
传统的主成分分析可以较好地处理变量间的线性关系,但是当处理的数据呈现出非线性关系时,会导致各主成分贡献率过于分散,不能找到有效代表原样本的综合变量,处理效果不够理想[10].基于核技巧的主成分分析是一种较为理想的处理非线性问题的方法,其基本原理如下所述.
令原始样本数据矩阵为
X=(xij)n×p,i=1,2,…,n;j=1,2,…,p.
其中:xi=(xi1,xi2,…,xip)′为数据集的第i个样本,n为样本容量,p为变量个数.
给定非线性映射Φ,将低维空间中的样本映射到高维空间Y中,即
xi∈Rp→Φ(xi)∈Y.
在高维特征空间中利用主成分分析进行特征提取,使得原样本空间中线性不可分数据在新空间下线性可分,如图1所示.
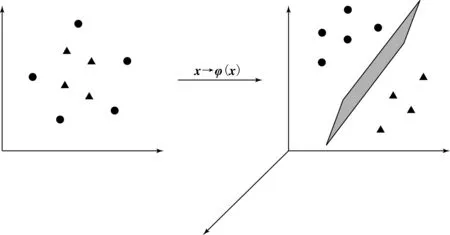
图1 KPCA样本分离原理示意图
核主成分分析计算过程如下:
令zi=φ(xi)为xi在高维特征空间中的样本,其协方差矩阵为
(1)
KPCA的求解目标为
(2)
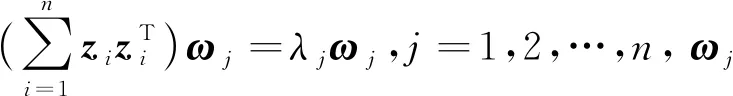
由于φ(x)形式一般未知,引入形式已知的核函数
κ(xi,xj)=φT(xi)φ(xj),
(3)
常用的核函数[11]:
(4)
(5)
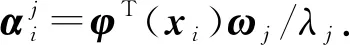
把(5)式带入(4)式可得
(6)
将(6)式两侧同乘φT(X)=(φT(x1),…,φT(xn))T可得
Kαj=λjαj.
(7)
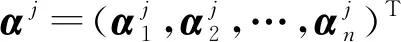
将(5)式带入(2)式最终得到核主成分解
(8)
在进行维度约减时,一般取前d(d 核主成分的主要目标是基于核函数对数据进行维度约减,那么核函数选择是否恰当就成为核降维的关键所在,这就需要不断探寻新的核函数以提高核降维效果,以提高后续机器学习分类算法的预测性能.受到柯西核函数的启发并依据如下定理1,本节构造新的伪柯西类核函数. 定理1[12]设f:X→R是有界可积连续函数,则k(x-x′)=f(x-x′)为核函数的充要条件是f(0)>0,且其傅里叶变换 定理2 令 (9) 则(9)式为核函数. 令t=-x,有 所以 因此 (10) 其中c>0,则(10)式为核函数. (11) 其中c>0,0 (9)—(10)式的表达形式与柯西密度函数较为相似,故本节构造的核函数称之为伪柯西类核函数,将上述核函数应用于高维数据的特征约减,通过实验分析将伪柯西类核函数与传统核函数的维度约减效果进行对比. 利用本文构造的伪柯西核函数以及已有的高斯核、多项式核、线性核、双曲正切核对真实数据集进行降维,然后采用目前主流的机器学习方法包括支持向量机(SVM)[13]、K近邻[14](KNN)、朴素贝叶斯(NB)[15]在降维后的数据集与原始数据上进行分类预测,最后将不同核函数的降维效果进行对比研究. 实验环境设置为:Windows10,64位操作系统,Intel i7-9 700、3.0 GHz CUP,16 GB内存,本文提出的算法和实验基于R语言(R 3.6.3)编码实现.使用来自Broad Institute Genome Data Analysis Center(http:∥portals.broadinstitute.org/cgi-bin/cancer/datasets.cgi)的4个真实癌症基因表达数据集进行实验分析,数据的基本信息如表1所示.为了评价不同维度下机器学习方法的分类性能,使用的性能度量指标为分类精度. 表1 数据集信息 基于核主成分分析的数据维度约减与分类识别步骤如下: ① 对数据集进行标准化处理,消除量纲的影响; ② 选取核函数以及设定核函数参数; ③ 依据步骤②的核函数计算核矩阵; ④ 计算核矩阵的特征值与特征向量并对特征向量进行归一化处理; ⑤ 依据(8)式,计算原始数据在高维特征空间中的核主成分解yj,j=1,2,…,d; ⑥ 依据yj,j=1,2,…,d,利用机器学习分类方法对原始数据进行分类识别. 由于本文所使用的核函数均带有参数,高斯核参数σ2,多项式核参数d,双曲正切核参数β和θ,本文构造的伪柯西核函数(10)式中的参数c,需要对上述参数进行合理设定,即经过上述核降维后,使得后续的机器学习分类性能达到相对最优.由于每个核函数至多包含2个参数,在参数不多的情况下,采取较为适宜的网格搜索(Grid Search)策略,对每个核函数中的参数设定取值范围并按等步长取值,使得后续分类算法达到精度最高的参数即为最终选取的参数.最终确定的参数分别为σ2=50,d=2,β=6,θ=-0.1,c=1.对比实验结果见表2—4. 表2 基于全变量、高斯核、多项式核、双曲正切核与伪柯西核的SVM五折交叉验证精度比较 表3 基于全变量、高斯核、多项式核、双曲正切核与伪柯西核的KNN五折交叉验证精度比较 表4 基于全变量、高斯核、多项式核、双曲正切核与伪柯西核的NB五折交叉验证精度比较 根据表2给出的实验结果可以看出,若不对原始数据进行降维,而直接应用SVM进行分类,在4个数据集上的精度仅有52%,31.88%,70%和19.33%,分类精度过低,这表明SVM对高维度小样本数据集异常敏感,因此有必要对数据进行维度约减.经过核降维后,其分类精度有了明显提升,与传统的高斯核、多项式核和双曲正切核相比,经过本文构造的伪柯西核函数降维后,SVM的分类精度达到最高分别为91.84%,98.79%,96.41%和98.05%.根据表3可以看到,伪柯西类核降维使得KNN的分类精度在Leukemia和Muliti-A数据集精度达到最高,在Breast和Lung数据集达到次最优.根据表4的结果,伪柯西类核降维使得NB在3个数据集上的分类精度达到最大,在1个数据集上精度达到次最大. 通过表2—4的实验结果,总体上可以得出,与全变量、高斯核、多项式核以及双曲正切核相比,经过伪柯西核类函数降维后可以使目前主流的机器学习方法如SVM、KNN和NB的分类性能有较为显著的提升.这表明,核降维可以较为充分的提取原始数据集的信息.通过在4个癌症基因表达数据上的数据分析,与传统核函数相比,伪柯西核的降维效果要更为出色. 针对数据集高维度、高冗余性特点,为了提高后续机器学习算法的分类性能且能够降低分类预测过程中的复杂度,本文提出一种基于伪柯西类核函数的主成分降维方法,即构造新的核函数对高维数据进行维度约减.通过在4个癌症基因表达数据集的实验分析,与全变量、高斯核、多项式核以及双曲正切核相比,在多数情况下,伪柯西类核函数可更为有效地提高主流机器学习方法的预测精度.2 伪柯西类核函数
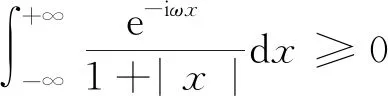
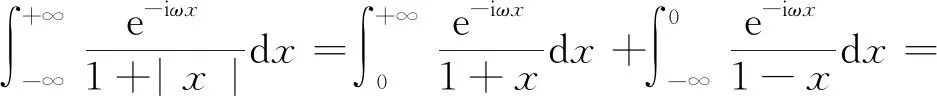
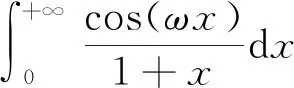
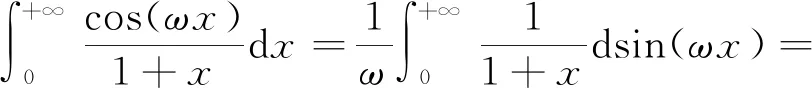

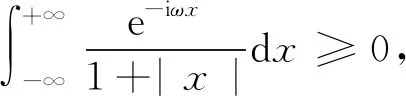
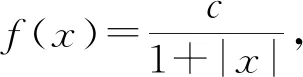
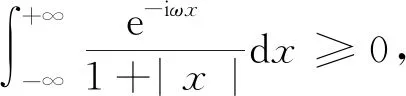
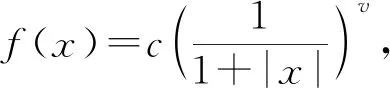
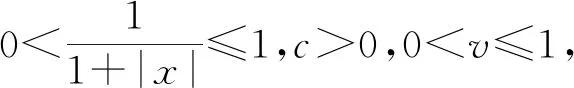
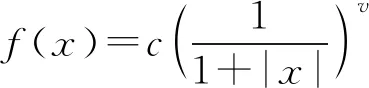
3 实验结果与分析
3.1 实验设计

3.2 对比实验结果与分析



4 结论
