无人机载北斗反射信号的海面测高性能评估
2021-10-15马德皓孟婉婷盛志超杨树瑚
张 云,马德皓,孟婉婷,秦 瑾,盛志超,杨树瑚*
(1.上海海洋大学信息学院 上海市海洋智能信息与导航遥感工程技术研究中心,上海 201306;2.上海航天电子技术研究所 上海 201109)
0 引言
海面高度是海洋科学研究领域中的重要一环,全球导航卫星系统卫星反射(Global Navigation Satellite Systems-Reflectometry,GNSS-R)是一种发展较快的遥感海面高度测量技术,该技术通过计算反射信号与直射信号之间的延迟差来反演海面高度。相对于传统的遥感技术,GNSS-R技术有成本低、实时监测、拥有大量信号源和不受天气影响等优点。这些优点受到全球相关学者的关注,并开展了广泛的研究[1]。
GNSS-R海面高度反演平台包含岸基平台[2-3]、船载平台、机载平台和星载平台。机载平台相对于岸基平台,具有监测范围广的特点,同时机载平台的技术为星载平台提供了大量的技术支持。2012年,Fabra等人[4]使用机载平台在3 000 m高度进行实验,对采集的芬兰湾海域的C/A码与P(Y)码数据进行分析,海面高度反演结果达到了厘米级精度;2018年,樊梦文等人[5]通过理论测高模型,利用机载GNSS仿真反射信号,对比了C/A码和P(Y)码的测高精度,发现基于半无码的P(Y)码自相关的测高精度相对于C/A码自相关和信号互相关测高精度分别提高了4.97倍和2.47倍;2019年,张杨阳等人[6]依据码测高原理建立机载测高模型,通过分析2011年11月11日,CSIC-IEEC在芬兰波罗的海的GNSS-R机载数据,得到米级反演精度。近年来北斗导航卫星系统(BeiDou Navigation Satellite System,BDS)发展为GNSS-R技术的应用提供了更多可能。BDS是可以为全球用户提供全天候、全天时、高精度的定位、导航和授时服务的国家重要时空基础设施,是GNSS-R的重要信号源之一。2015年,张云等人[7]在中国东海海域使用岸基BDS-R进行海面测高实验,得到了均方根(RMS)为0.37 m的反演精度;2018年,杭斯加等人[8]使用相位测高方法对北斗IGSO卫星反射信号数据进行分析,得到的岸基海冰厚度反演精度为厘米级。岸基平台的BDS-R测高研究较多,但是基于机载平台的BDS-R海面高度测量的研究较少[7,9],缺少必要的实验成果及分析。
近年来,无人机的快速发展给予GNSS-R机载观测平台更大的发展空间,本文在前期岸基平台BDS-R海面测高反演研究的基础上,对BDS-R的B1/B3频段的无人机载海面测高进行了研究。旋翼无人机搭载自研的微小型北斗反射信号探测仪,利用接收的海面多普勒时延图(Delay Doppler Map,DDM)数据,建立了DDM测高模型和误差模型,实现海面高度反演。反演结果分别与实测的探测仪至海面高度和全球海面高度模型结果对比,验证海面高度反演的精度。对同一区域海域进行了连续3次飞行实验,验证了机载海面测高模型的有效性,评估了B1/B3频段的无人机载BDS-R在海面高度反演应用中的反演精度,证明了自研微小型北斗反射信号探测仪的有效性。
1 BDS-R探测仪
1.1 北斗信号调制与结构
BDS采用L波段右旋圆极化信号,由I、Q两个支路的测距码和导航电文正交调制在载波上构成B1、B2、B3信号,3种信号又细分为B1I、B1C、B2A和B3I等,本次实验采用B1I和B3I两个频段信号。
B1I信号采用二进制相移键控(BPSK)调制,标称载波频率为1 561.098 MHz。信号由“测距码+导航电文”调制在载波上构成,信号表达式为:
(1)
式中,j表示卫星编号;AB1I表示 B1I 信号振幅;CB1I表示 B1I的信号测距码;DB1I表示调制在B1I信号测距码上的数据码;f1表示B1I信号载波频率;φB1I表示B1I信号载波初相。
B3I信号采用二进制相移键控(BPSK)调制。标称载波频率为 1 268.520 MHz。信号由“测距码+导航电文”调制在载波上构成,信号表达式为[10]:
(2)
式中,j表示卫星编号;AB3I表示B3I信号振幅;BB3I表示B3I的信号测距码;DB3I表示调制在B3I信号测距码上的数据码;f3表示B3I信号载波频率;φB3I表示B3I信号载波初相。
1.2 微小型北斗反射信号探测仪
无人机搭载的有效载荷需要具有质量轻、功耗低、成本低等优点。针对这一特性,本文采用的硬件为上海航天电子技术研究所设计研制的微小型北斗反射信号探测仪,由右旋圆极化(RHCP)上视天线、左旋圆极化(LHCP)下视天线和DDM接收机3部分组成。RCHP上视天线,可接收BD-2 B1/B3频段信号,天线增益为3 dBi,波束宽度为120°;LCHP下视天线,可接收BD B1/B3频段信号,天线增益为15 dBi,波束宽度为40°。微小型北斗反射信号探测仪的结构示意如图1所示,最终生成的DDM数据将用于海面高度反演。
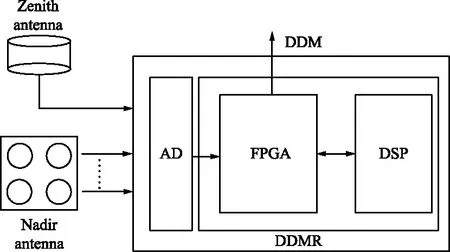
图1 微型GNSS-R探测仪结构示意Fig.1 Structure diagram oftiny GNSS-R detector
2 无人机载BDS-R海面高度反演
2.1 海面高度反演原理
本文的机载北斗GNSS-R海面高度反演几何原理如图2所示,参考椭球采用CGCS2000椭球体。

图2 机载北斗GNSS-R海面高度DDM反演原理Fig.2 DDM inversion principle of airborne Beidou GNSS-R sea surface height
北斗卫星与机载探测仪之间的直射延迟时间为Dir,在海面上的反射信号延迟为Ref[11],可得:
Delay=(Ref-Dir)×c,
(3)
式中,Delay表示北斗卫星与机载探测仪在海面上的反射信号与直射信号延迟距离差;c为光速;结合镜面反射点仰角E,可得到初步反演的探测仪至海面的高度Hrmeasured:
(4)
通过GNGGA数据得到的上视天线的椭球高度Hdir、上视天线与下视天线的垂直距离Hantenna和Hrmeasured可知,反演的海面高度的椭球高SSHmeasured为:
SSHmeasured=Hdir-Hantenna-Hrmeasured。
(5)
式(3)和式(4)的成立基于下列假设:
① GPS卫星与探测仪卫星距离海面足够远,因此海面与椭球面间的反射仰角差异可忽略不计;
② 海面的反射点为平面[12]。
2.2 海面高度反演的误差分析
无人机载BDS-R信号在传播过程中,会因为各种因素导致信号传播出现误差。这些因素若不进行分析与修正,将会导致海面高度反演精度的下降,因此有必要对误差进行分析并加以修正。
电离层误差:电离层对信号传输有较大影响,但由于电离层位于60 km以上的空间,而无人机载平台高度为距离地面约50 m内,无人机机载平台所接收到的直射信号与反射信号都经历了相似的下行传输路径,故直射信号与反射信号的电离层延迟近乎相等,因此本文在计算时忽略电离层误差。
对流层误差:对流层为底层大气层,主要分布在距离地面15 km的空间中。本文实验数据均来源于海面,海面的水蒸气等对信号的传输影响较大,且反射信号与直射信号在低空经历了不同的传输路径,本文对对流层误差(Delaytro)的修正如下[13-14]:
(6)
天线基线误差:本文使用的探测仪平台为旋翼式无人机,无人机在风速较小环境的飞行过程中,仅会发生轻微倾斜,因此姿态对天线基线的距离影响较小,因此本文在计算时,天线基线误差(Delayantenna)定义为无人机机载平台的上视天线与下视天线的垂直距离对应的延迟距离。
接收机单点定位(SGPS)误差:由于本文使用单点定位结果作为上视天线的椭球高度Hdir(式(5)),因此存在米级误差。
地球曲率误差:由于无人机平台飞行最高高度距离海面不高于100 m,因此地球曲率对实验的影响极小,故计算中忽略地球曲率误差。
综上,无人机机载BDS-R海面高度反演误差的延迟距离Delayerror为:
Delayerror=Delay-Delayantenna-Delaytro。
(7)
2.3 海面高度反演的精度验证方法
机载BDS-R海面高度反演结果需要进行对比验证来确定反演的精度。本文使用了2种数据进行验证:实测的探测仪相对于海面的高度数据和全球海面高度模型数据。
2.3.1 实测探测仪下视天线相对于海面高度数据验证
使用海面测高仪结合上视天线GNGGA等现场实测数据,计算出探测仪下视天线相对于海面高度数据进行精度验证。如图3(a)所示,在本文实验中,由于探测仪上视天线接收到了上视数据GGA,可以确定上视天线的实时椭球高Hdir;通过实时海面测高仪(图3(b))可得到测量的探测仪下视天线与海面的高度差Hsea,并结合海面测量仪的椭球高Hinstrument与上视天线与下视天线的垂直高度差Hantenna,可确定探测仪下视天线距离海面的实时高度Hrfield:
Hrfield=Hdir-Hantenna-(Hinstrument-Hsea)。
(8)
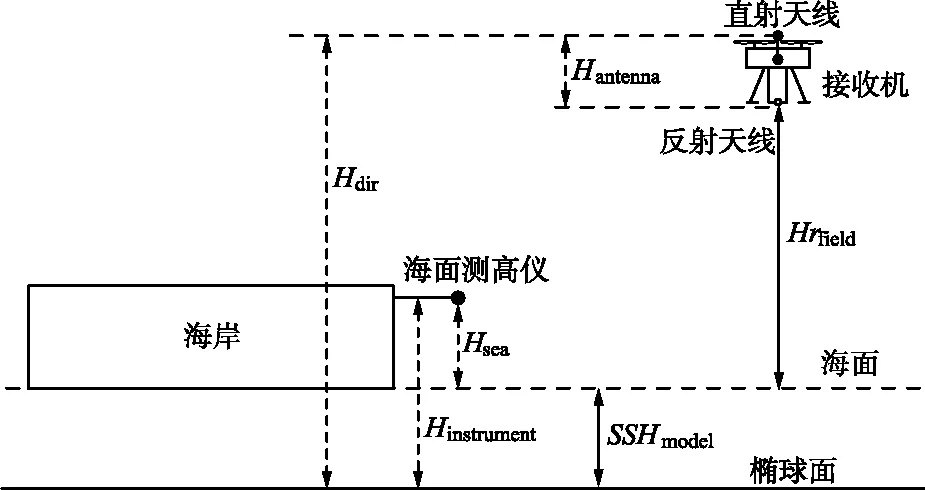
(a) 验证模型高度计算的几何示意

(b) 海面测高仪的安装位置图3 验证模型几何示意图及海面测高仪安装位置Fig.3 Geometry of the validation model and installation position of the sea level altimeter
得到的实测Hrfield与反演的探测仪下视天线相对于海面高度Hrmeasured(式(4)的结果)对比,得到反演精度△Hr。
2.3.2 海面高度验证模型
在计算模型海面高度时,使用由丹麦技术大学开发的DTU18全球平均海面模型(DTU Mean Sea Surface 18,DTUMSS18)与DTU全球海潮模型(DTUTide)组成的DTU模型[15-16]作为海面高度验证模型。由海面高度验证模型得到的海面椭球高SSHmodel为:
SSHmodel=DTUMSS18+DTUTide。
(9)
得到的SSHmodel与反演的海面高度SSHmeasured(式(5)的结果)对比,得到海面高度的反演精度△SSH。
2.4 无人机机载数据处理
无人机机载BDS-R海面高度反演方法流程为图4所示。
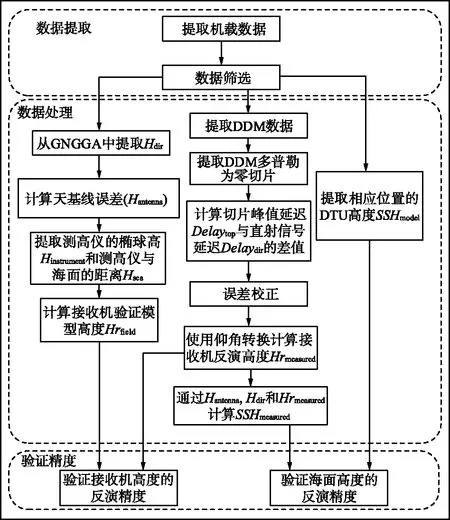
图4 机载BDS-R海面高度反演方法流程Fig.4 Flow of airborne BDS-R sea surface height inversion method
① 数据筛选:提取机载数据并进行数据筛选,筛去仰角低于30°的数据,并去除镜面反射点位于陆地上的观测数据和观测波形出现明显异常的数据[15],然后对筛选后的数据进行后续处理。
② 数据反演:首先对DDM数据进行计算。使用无人机机载数据中的B1/B3频段的DDM数据(如图5所示),提取其中多普勒维度为零的波形切片(如图6所示)。对比图6的B1和B3的波形切片,可以发现B3频段延迟宽度(约100 m)小于B1频段(约300 m),说明B3频段信号具有更好的抗干扰性;而B1频段信号具有更强的信号强度。2个频段信号都具有各自的优势。
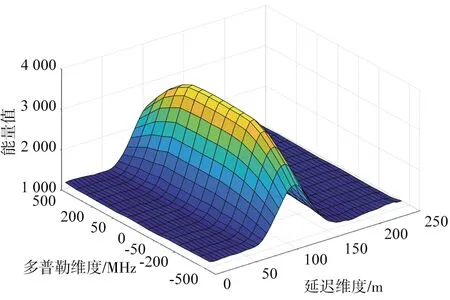
(a) B3 DDM图
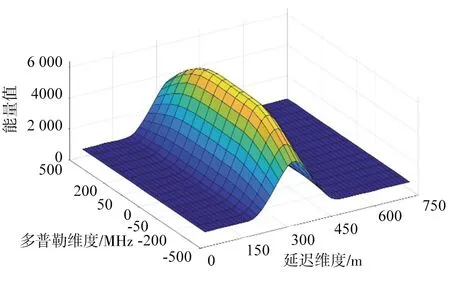
(b) B1 DDM图图5 B3和B1的DDM例图Fig.5 DDM diagram of B3 and B1
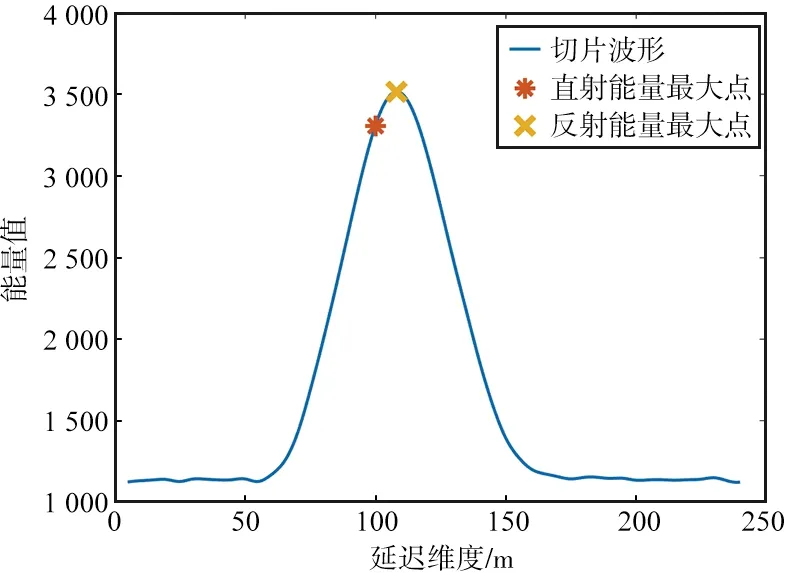
(a) B3 DDM切片

(b) B1DDM切片图6 B3和B1的DDM切片Fig.6 DDM section of B3 and B1
在无人机机载实验中,由于探测仪距离海面较近,因此直射信号能量最大值与反射信号能量最大值的均落在了DDM时延窗中[17-18]。直射信号能量最大值在DDM窗口中对应的延迟距离为Delaydir,而反射信号能量最大值为DDM多普勒为零切片中峰值所对应的位置,在DDM窗口中的延迟距离为Delaytop,2个点在波形中的位置如图6所示。因此,式(3)在DDM反演中可变形为:
Delay=(Ref-Dir)×c=
Delaytop-Delaydir。
(10)
结合式(3)、式(4)与式(7)可知,机载BDS-R海面高度反演的探测仪下视天线到海面的高度Hrmesured为:
(11)
③ 结果验证:结合2.3.1节,通过探测仪上视天线提供的GNGGA数据,可得到实测的探测仪下视天线距离海面高度Hrfield。通过Hrfield与Hrmeasured可知,反演的平均绝对误差 (Mean Absolute Error,MAE)与均方根误差(Root-Mean-Square Error,RMSE)为:
ΔHr=|Hrmodel-Hrmeasured|,
(12)
(13)
(14)
式中,HrMAE为反演的探测仪至海面高度的全部样本的平均绝对误差;HrRMSE为反演的探测仪至海面高度的全部样本的均方根误差,N为样本数量,I= 1,2,3,…,N。
结合2.3.2节,通过镜面反射点经纬度数据,结合DTU18全球平均海面模型与DTU全球海潮模型组成的DTU模型,可以得到海面高度验证模型的椭球高SSHmodel。通过SSHmodel与SSHmesured可知反演的MAE与RMSE为:
ΔSSH=|SSHmodel-SSHmeasured|,
(15)
(16)
(17)
式中,SSHMAE为反演的海面高度的全部样本的平均绝对误差;SSHRMSE为反演的海面高度的全部样本的均方根误差,N为样本数量,i= 1,2,3,…,N。
3 实验结果分析
3.1 实验环境
2020年9月6日,于山东省威海市山东大学威海分校北门,金海湾国际饭店栈桥(37°32′2.483 9″N,122°2′44.154 4″E)附近的黄海海域进行了BDS-R无人机机载实验。机载探测仪在实验过程中,进行了三段实验,每段实验的时间段与接收数据种类如表1所示。使用手持测风仪进行了风速测量。

表1 实验时间段Tab.1 Experimental time period
实验使用的无人机为大疆无人机BDA型,表2为无人机具体参数。如图7所示,探测仪上视天线与下视天线分别安装于无人机顶部与底部。其中,上视天线与下视天线的几何中心距离,即Hantenna(式(7)Delayantenna)为0.64 m。
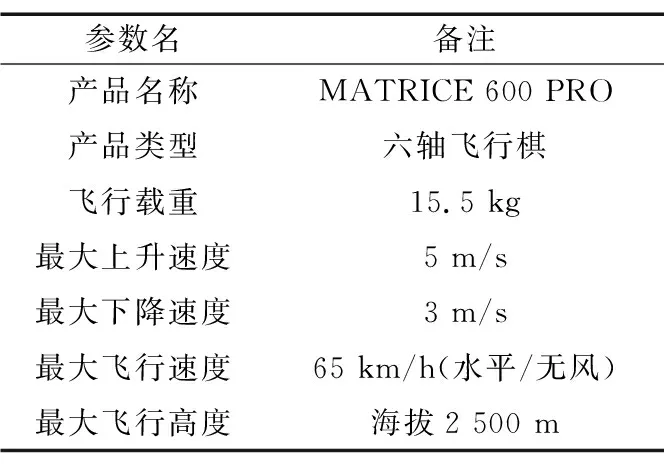
表2 无人机参数Tab.2 UAV parameters

图7 无人机Fig.7 Unmanned aerial vehicle(UAV)
3.2 机载BDS-R海面高度反演结果分析
3.2.1 第一段数据实验结果
为了消除地面等因素造成的影响,选取无人机位于海面区域的数据进行反演实验分析。探测仪接收到的数据分为四通道,本文在反演计算时,将四通道反演结果进行平均得到最终反演结果。
本文的第一段实验时间为2020年9月6日11∶58—12∶19(北京时间),持续时间为21 min。筛选后,共保留了442个样本点。使用2.3节与2.4节的方法,分别计算反演的探测仪至海面高度Hrmeasured,实测探测仪至海面高度Hrfield,反演的海面高度SSHmeasured,模型的海面高度SSHmodel。图8(a)为对应数据的无人机空中段飞行轨迹,红色箭头为飞行方向;图8(b)为实验对应的卫星天顶图;图8(c)为实验对应的镜面反射点轨迹图。
饱和度指道路实际通行能力与该路段通行能力的比值,反映了道路的实际服务水平,通常用v/c表示.因为调查区域路段较多,要比较不同组织方案的影响就要对周围道路的饱和度进行加权平均:

(a) 第一段数据无人机飞行轨迹

(b) 第一段数据的卫星天顶图
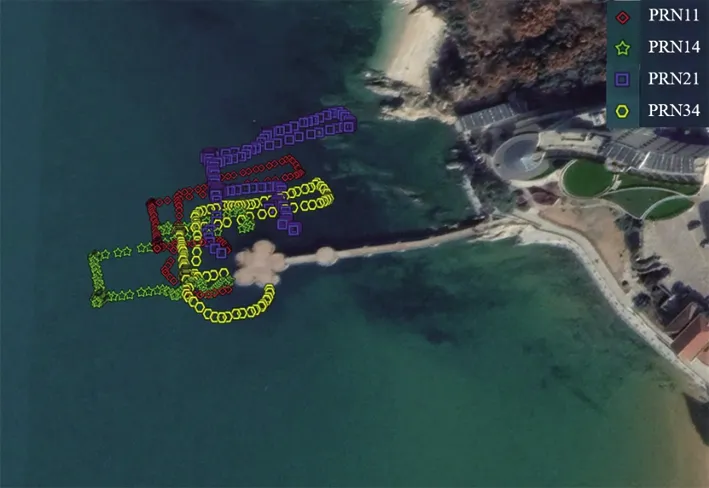
(c) 第一段数据的镜面反射点轨迹图8 第一段无人机数据Fig.8 UAV data of the first segment
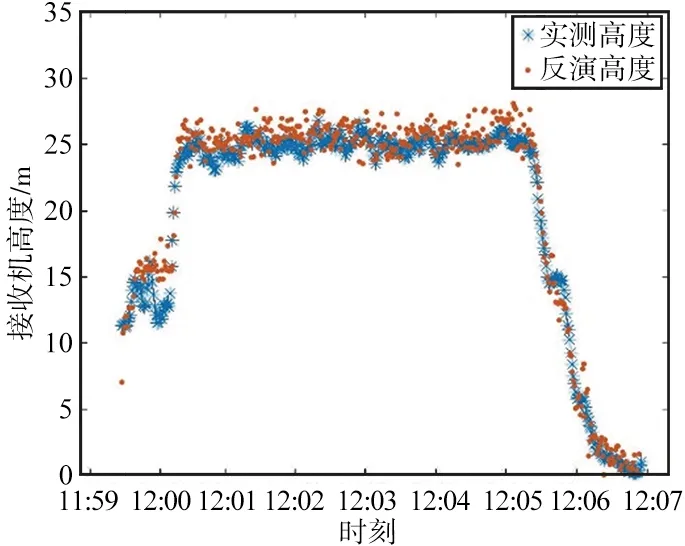
第一段数据的反演结果与实测结果对比如图9所示,蓝色为实测探测仪至海面高度,橙色点为反演的探测仪至海面高度结果。第一段数据的反演结果与模型结果对比如图10所示,蓝色线为DTU海面高度验证模型高度结果,橙色点为反演的海面高度结果。
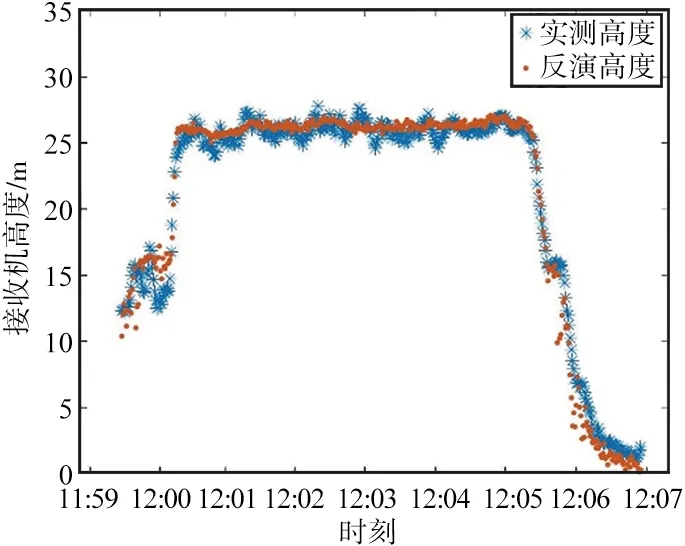
(a) B3
(b) B1图9 第一段数据的反演结果与实测结果对比Fig.9 Comparison of the inversion and measured results provided by the first segment of data
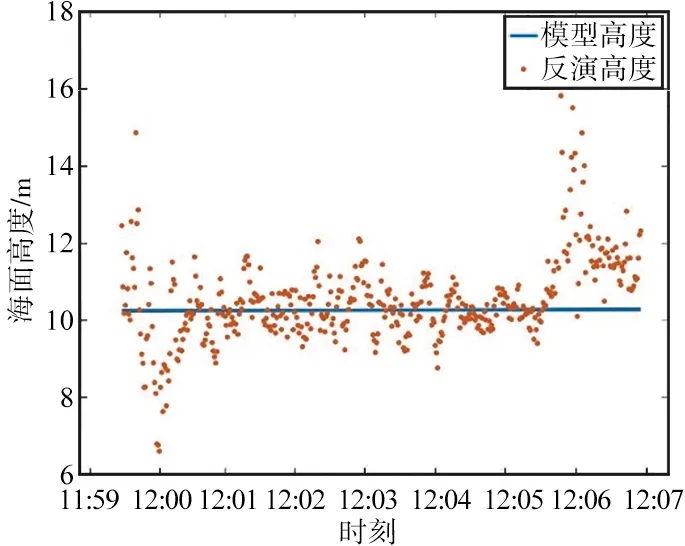
(a) B3

(b) B1图10 第一段数据的反演结果与模型结果对比Fig.10 Comparison of the inversion and model results provided by the first segment of data
3.2.2 第二段数据实验结果
本文的第二段实验时间为2020年9月6日12:31—12:51(北京时间),持续时间为20 min。筛选后,共保留了786个样本点。图11(a)为对应数据的无人机空中段飞行轨迹,红色箭头为飞行方向;图11(b)为实验对应的卫星天顶图;图11(c)为实验对应的镜面反射点轨迹图。

(a) 第二段数据无人机飞行轨迹

(b) 第二段数据的卫星天顶图

(c) 第二段数据的镜面反射点轨迹图11 第二段无人机数据Fig.11 UAV data of the second segment
第二段数据的反演结果与实测结果对比如图12所示,蓝色为实测探测仪至海面高度,橙色点为反演的探测仪至海面高度结果;第二段数据的反演结果与模型结果对比如图13所示,蓝色线为海面高度验证模型高度结果,橙色点为反演的海面高度结果。

(a) B3
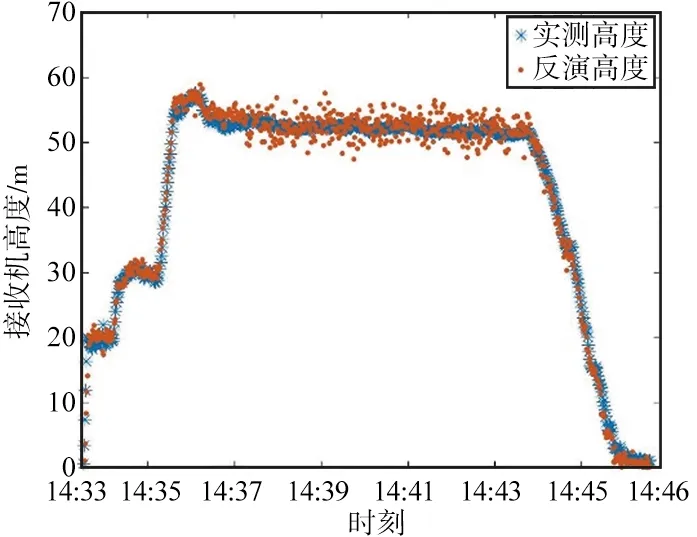
(b) B1图12 第二段数据的反演结果与实测结果对比Fig.12 Comparison of the inversion and measured results provided by the second segment of data

(a) B3
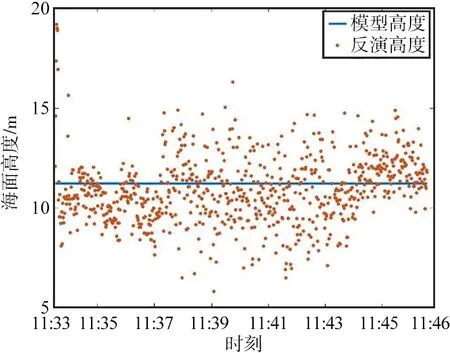
(b) B1图13 第二段数据的反演结果与模型结果对比Fig.13 Comparison of the inversion and model results provided by the second segment of data
3.2.3 第三段数据实验结果
本文的第三段实验时间为2020年9月6日15:09—15:20(北京时间),持续时间为11 min。筛选后,共保留了535个样本点。图14(a)为对应数据的无人机空中段飞行轨迹,红色箭头为飞行方向;图14(b)为实验对应的卫星天顶图;图14(c)为实验对应的镜面反射点轨迹图。

(a) 第三段数据的无人机飞行轨迹
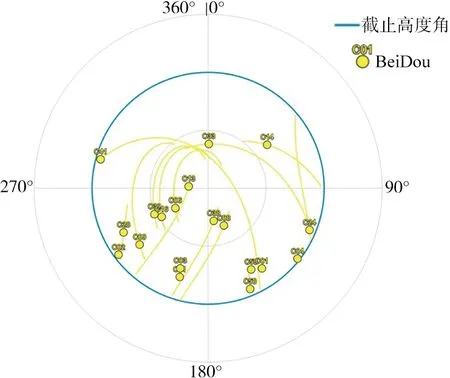
(b) 第三段数据的卫星天顶图
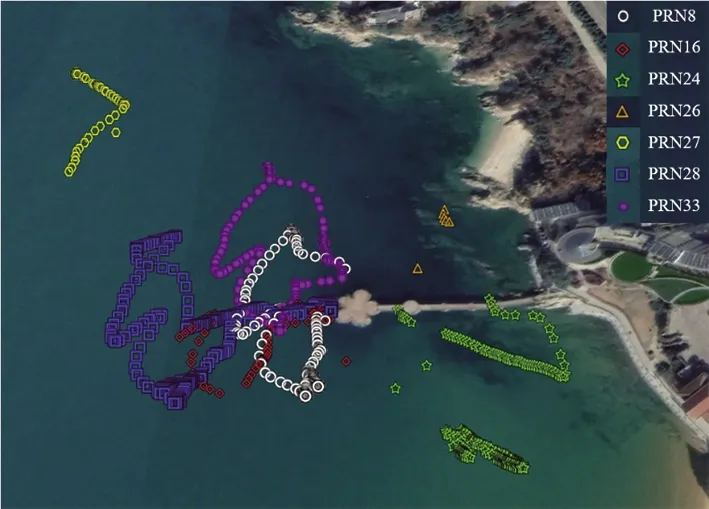
(c) 第三段数据的镜面反射点轨迹图14 第三段无人机数据Fig.14 Data of the third segment
第三段数据的反演结果与实测结果对比如图15所示,蓝色为实测探测仪至海面高度,橙色点为反演的探测仪至海面高度结果;第三段数据的反演结果与模型结果对比如图16所示,蓝色线为海面高度验证模型高度结果,橙色点为反演的海面高度结果。

(a) B3

(b) B1图15 第三段数据的反演结果与实测结果对比Fig.15 Comparison of the inversion and measured results provided by the third segment of data
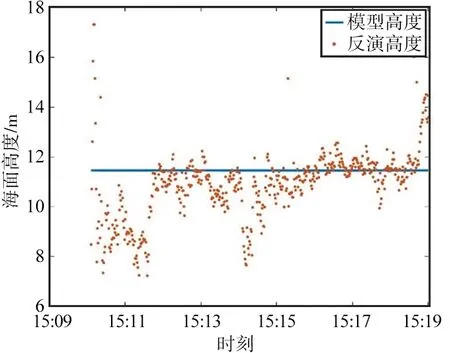
(a) B3

(b) B1图16 第三段数据的反演结果与模型结果对比Fig.16 Comparison of the inversion and model results provided by the third segment of data
3.2.4 实验结果分析
三段实验的B1/B3频段反演结果的总体精度如表3所示。

表3 反演精度Tab.3 Inversion accuracy 单位:m
总结三段数据的反演结果对比图和表3的结果:
① 从探测仪相对于海面高度反演结果对比图(图9、图12、图15)可以得出,B1和B3反演结果均能够较好地反映无人机的高度变化;从海面高度反演结果对比图(图10、图13、图16)可以得出,B1和B3的反演结果均能较好地反映海面高度变化。
② B3频段的反演结果可以达到更高的精度以及稳定性,即MAE与RMSE均总体较小,这和B3频段信号具有更好的抗干扰性(图6)有关。
③ 由于无人机在飞行过程中受到海风影响,特别是在上升和下降途中,会出现探测仪天线晃动等情形,因此从三段数据的反演结果对比图中(图9~图10,图12~图13,图15~图16)可以发现,无人机在上升与下降期间,反演结果相较于验证模型出现了较大波动,误差增大;而在飞机平稳飞行期间反演结果相较于验证模型的波动较小,误差减小。未来,尽量使用平稳飞行状态下的数据进行海面高度反演。
④ 上视天线的椭球高度Hdir(式(5))中存在着单点定位误差,也会对最终结果造成影响。未来,使用高精度RTK探测仪结果可以获得更高精度的反演结果。
⑤ 反演结果与全球海面高度模型(SSH结果验证)和实测数据(Hr结果验证)对比,都得到亚米级精度,其中实测数据对比更适用于有条件的小海域近岸的反演结果的实测精度验证。
4 结束语
本文主要对无人机载BDS-R的B1/3频段信号的海面测高进行了研究。2020年9月6日于威海开展了无人机BDS-R机载实验,采用自研微小型北斗反射信号探测仪,采集B1/B3频段的BDS-R的海面DDM数据,在DDM测高模型基础上,实现了无人机机载北斗GNSS-R海面高度测量模型,通过计算反射信号相对于直射信号的延迟距离(DDM多普勒为零窗口中能量峰值所对应的延迟距离与理论直射信号能量最大值点所对应的延迟距离的差),进一步反演并结合误差模型修正获得探测仪下视天线至海面的高度,最终结果分别与实测数据与DTU全球海面高度模型结果进行精度验证,并且对B1和B3的反演结果做了比较。B1频段反演的探测仪高度的MAE为1.55 m,RMSE为1.96 m;海面高度的MAE为1.69 m,RMSE为2.10 m;B3频段反演的探测仪高度的MAE为0.88 m,RMSE为1.24 m;海面高度的MAE为1.15 m,RMSE为1.50 m。结果证明,B1和B3频段的反演结果均能较好地反映海面高度,由于B3信号的抗干扰强,B3频段的反演精度更高。实验同时验证了开发的微小型北斗反射信号探测仪的有效性,评估了无人机机载北斗BDS-R的B1和B3频段在海面高度反演的精度。
