基于GRU改进RNN神经网络的飞机燃油流量预测
2021-10-15李乐乐杨鑫涛
陈 聪, 候 磊, 李乐乐, 杨鑫涛
(1.中国民航大学航空工程学院, 天津 300300; 2.北京航空航天大学航空科学与工程学院, 北京 100191; 3.北京航空航天大学能源与动力学院, 北京 100191)
近年来,在“全面建设民航强国”的构想下,航空企业以做到“低碳运营、环境友好、资源节约”为节能减排的发展目标,各航空公司面临着巨大挑战。燃油流量(fuel flow, FF)是影响飞行性能的重要参数和衡量航空发动机的主要性能参数之一,对于发动机在不同航班中的燃油流量变化的跟踪能够反映发动机性能的故障和衰退情况[1]。
快速存储记录器(quick access recorder, QAR)数据是监控发动机异常状态和评估飞机飞行品质评估的重要数据来源,这些数据蕴藏丰富发动机健康信息和环境信息,在一定程度上能够反映发动机的部分控制规律[2]。QAR数据实时记载了飞行轨迹、状态以及环境参数等反映飞行情况的参数。对QAR大数据的挖掘和研究有利于寻找影响FF的规律,监测发动机的工况。当发动机发生故障或性能衰退时,排气温度(exhaust gas temperature,EGT)、燃油流量FF和转速等气路参数实际测量值将会发生变化[3],由此可对飞行品质进行监控,并进行故障排除与故障诊断。
神经网络在人工智能和大数据挖掘领域有着广泛应用,使用神经网络对飞机机载系统进行预测与健康管理是飞机智能化的重要研究方向[4],也是实现民航智能化的重要工具。
为了保证飞机的高综合保障性、高可靠性、高安全性以及高运营效益,自20世纪90年代陆续开始了复杂装备预测与健康管理(prognostics and health management,PHM)系统研究[4]。目前,B737NG是中国航空公司最广泛使用的机型之一,受机载电子设备、传感器网络、空地数据链系统等限制无法使用PHM系统。在此情况下,对QAR数据的分析和监控结果成为了燃油流量研究等领域的重要依据,也成为了保障飞行安全、减少燃油消耗、提高飞机运营效率的科学技术手段。
在利用QAR数据进行燃油流量预测的领域,中外已经有许多相关研究。谷润平等[1]根据最小二乘法提取出了影响发动机燃油流量的主要因素。耿宏等[5]利用多元分析方法,建立了飞机巡航阶段左、右发燃油流量的线性回归模型。张金柱等[6]使用回归分析的方法,得出燃油流量受多因子影响的结论,并用最佳子集回归法获得了燃油流量回归方程。
神经网络对多个相关参数有良好的非线性映射能力,在多个领域都有运用。刘婧[7]在能量平衡原理的基础上,利用BP(back propagation)神经网络建立了不同阶段飞机燃油消耗的精确模型。陈聪等[8]采用熵权法建立了BP神经网络模型和回归模型的飞机燃油消耗组合模型。牟永强等[9]将真实货架场景中提取到的特征图送入多任务循环神经网络层学习并进行编码,提高了价格牌识别的精度。Raol等[10]通过循环神经网络网络分别在模拟数据集和实际数据集上估计了飞机的横向运动参数。Babaev等[11]采用循环神经网络对零售商进行了信贷评分。Miao等[12]使用深度循环神经网络构建了端对端语音识别系统。Selvin等[13]使用循环神经网络建立了股票预测模型。人工神经网络(artificial neural network,ANN)极大推进了人工智能领域的相关研究,近几年已成功地解决了机器学习、深度学习等领域的复杂实际问题。
1 主控参数选取与数据预处理
针对从QAR数据中获取的海量数据,设计研究了一种利用RNN神经网络进行飞机燃油流量预测的模型。首先对QAR数据选用皮尔逊相关性系数对燃油流量进行相关性分析,结合发动机控制原理,提取出对燃油流量有较大影响的参数,例如,排气温度EGT,油门杆角度TLA,发动机转速N1、N2,马赫数Ma,大气总温TAT,飞行高度H等。构建朴素RNN燃油流量预测模型,随后将数据喂入RNN网络供其学习,使用BPTT算法训练网络,Adam优化算法加速更新损失函数梯度。在Seq参数调整实验时发现RNN网络对历史信息利用能力不足,极易发生梯度消失与梯度爆炸等问题,遂提出改进网络结构重构,引入门控循环单元GRU重构预测模型。选取短程、中远程、远程航班来验证模型的准确性与适用性,并将由朴素RNN网络和GRU网络建立的燃油流量模型进行对比分析,探讨将该预测模型用于故障诊断等实用场景的可行性。论文研究流程如图1所示。
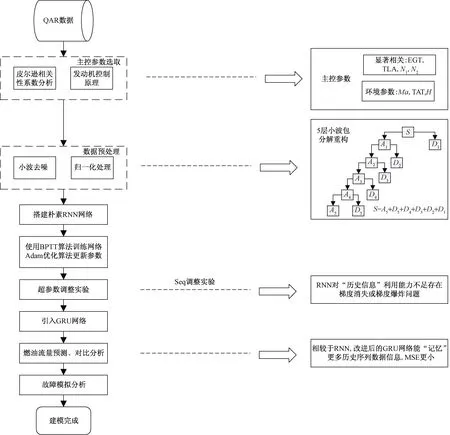
图1 研究流程Fig.1 Research process
1.1 发动机控制原理
在现代民航客机上,通常由飞行管理系统(flight management and control system, FMCS)负责飞行性能管理与飞行总体规划,一个典型的FMCS结构形式如图2所示。该系统的核心部件主要包括:控制显示组件(control display unit, CDU)和飞行管理计算机(flight management system, FMC)。飞行管理系统本质是一个专家系统,该系统计算机内部预装有与飞机运行性能相关的数据库。当FMC的某些内置程序接收到相关的信号与参数时,FMC会自动计算当前所需的目标N1转速,计算值经过显示电子组件(display electronic unit, DEU)传给显示组件(display unit, DU)进行显示,同时,传输给发动机电子控制组件(electronic engine control, EEC)进行控制。
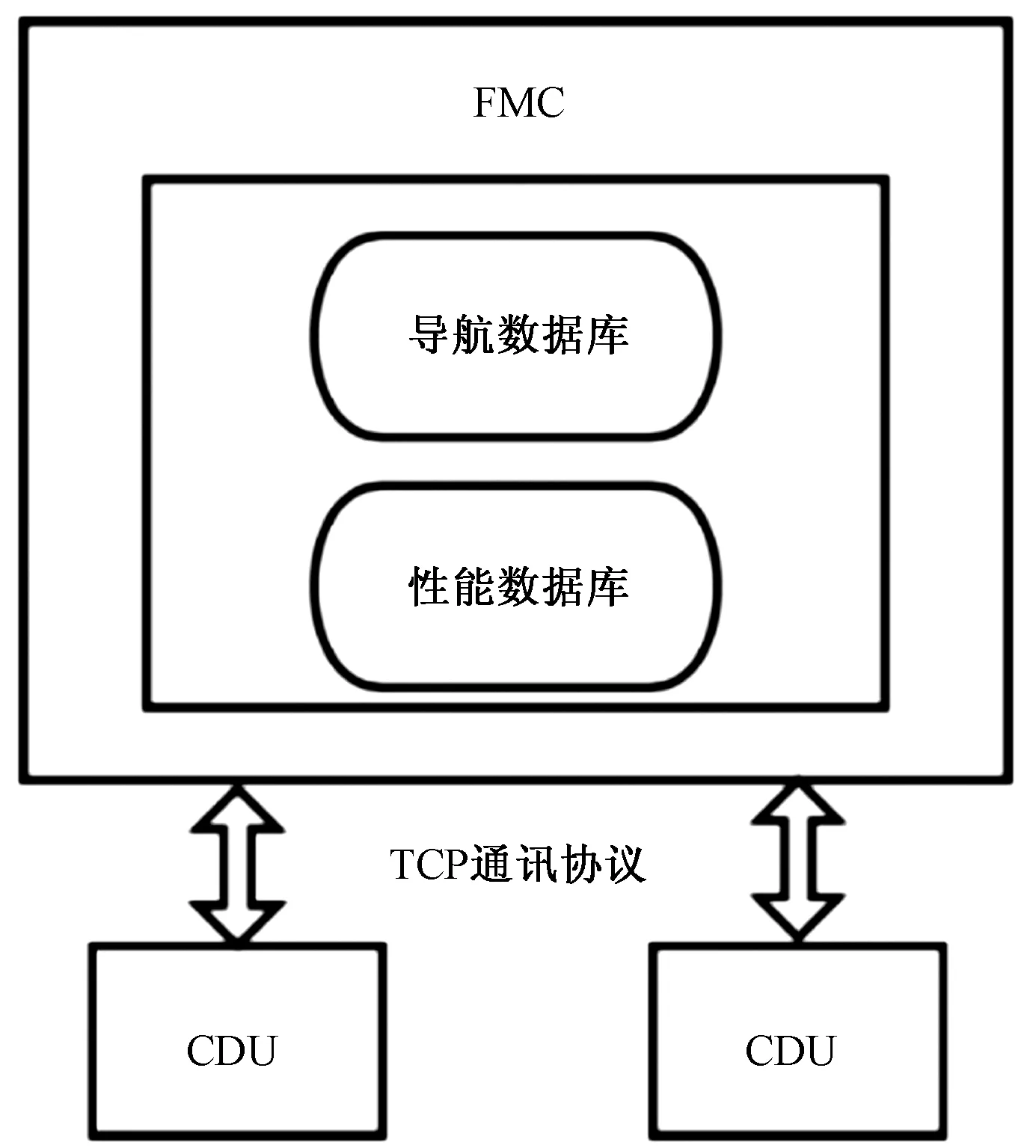
图2 典型FMCS构成Fig.2 Typical FMCS composition
对航空发动机推力的控制,本质是要实现对发动机燃油流量的控制。因此,计算机计算出目标N1转速之后,驾驶员可以选择通过手动油门杆选择适当的油门杆位置,或者通过自动油门杆(A/T)由飞行系统自动控制油门杆来获取对应的所需推力。在飞机起飞、爬升等状态,目标N1转速通常是发动机的极限转速;在巡航、下降等阶段,飞行管理系统会计算出最经济的飞行速度与N1转速。
EEC自动采集油门杆位置信号,综合考虑环境参数,计算并控制燃油计量活门(fuel metering value, FMV)的开度,从而控制发动机的转速。此外,EEC同时控制可变引气活门(variable bleed valve, VBV)、可变定子叶片(variable stator vane, VSV)、瞬时放气活门(transient bleed valve, TBV)、燃烧室压力CDP、温度传感器T20和T25、静压传感器Ps12和Ps3等部件[6],以确保发动机不超温、不超转,不超出贫、富油极限,压气机不喘振,同时保证发动机全流程工况的气动稳定性。
图3是燃油控制组件(fuel control unit, FCU)的工作流程示意图,结合以上分析可知:发动机N1转速、N2转速、发动机性能参数、环境参数等参数都能影响发动机燃油消耗。
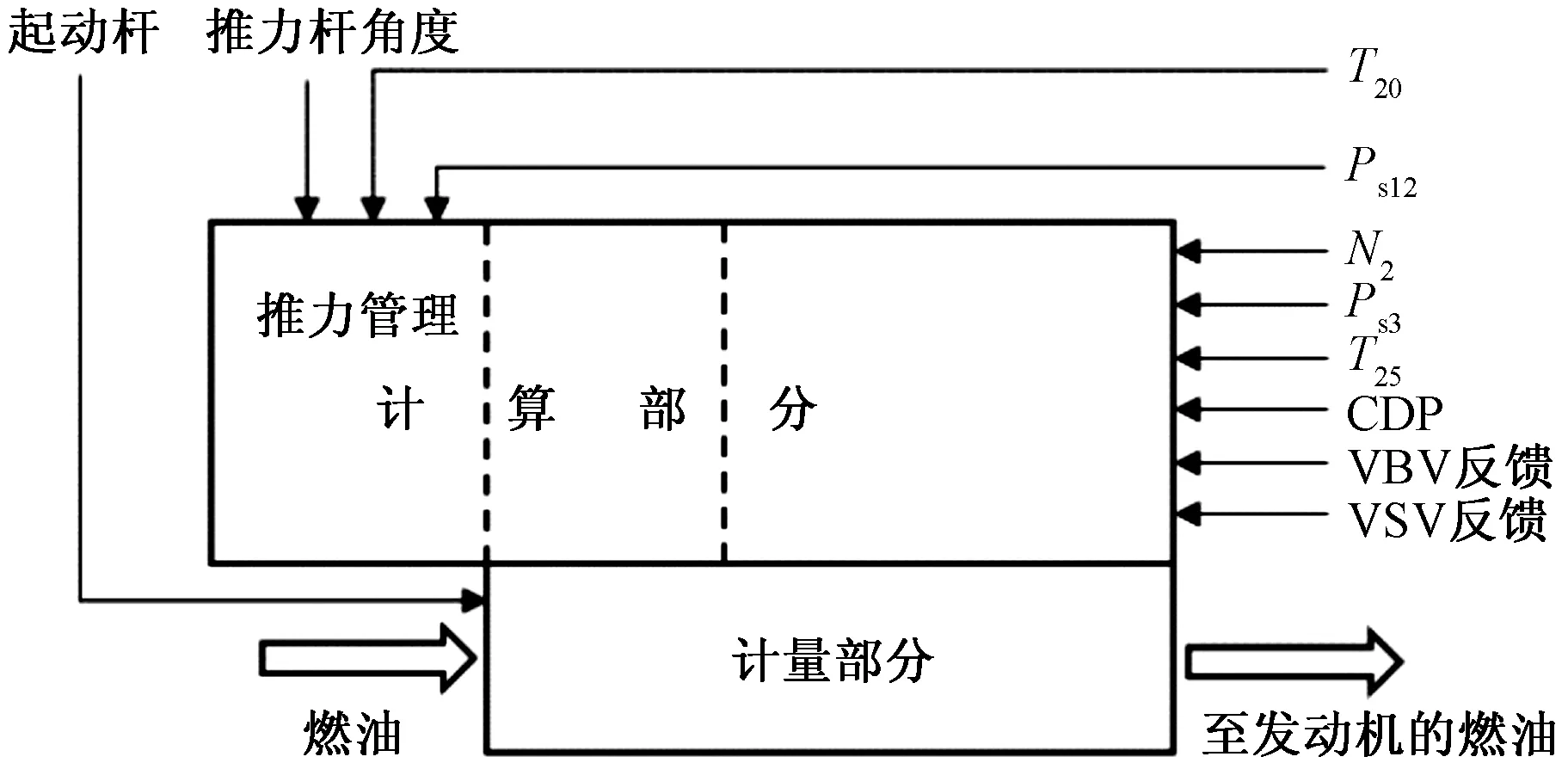
图3 燃油控制组件的工作流程图Fig.3 Flow chart of fuel control unit
1.2 QAR主控参数选取
快速存取记录器(QAR)中存储的大量数据是本次研究所需数据的来源,需要从中进行信息提取。QAR数据量极大、方便获取、获取成本低廉,其能记录飞机各部件的信息,包含丰富发动机信息和环境信息,其数据基本涵盖了发动机控制、加速处理器、燃油系统、滑油系统等多方面的性能参数。因此,QAR 数据在飞行品质分析、燃油流量研究等多个领域有很高的实际应用价值,由QAR 数据分析所得出的结论常常作为飞行品质监控与排故的重要依据。QAR的应用场景主要包括:为评价驾驶员的操纵品质提供数据支持和信息支撑;为发动机的维护提供监控数据与技术支撑;为飞行节省航油提供数据支持。
目前,QAR 数据已被广泛应用到飞机航空发动机状态监控和故障诊断等品质监控的实践中,为众多航空公司带来了极大的经济价值。相关应用集中在现代民航飞机上的各大系统,主要是针对气路参数(即发动机各气流通道中所测量到的参数)进行健康状态监控及性能分析[4]。因此,从大量广泛的QAR数据中提取出实用信息至关重要[14]。
对发动机燃油流量的影响因素众多,既包含发动机控制参数也包含环境参数,从QAR中选取对燃油流量产生较大影响的参数,将直接影响燃油流量预测的准确性和精度。
1.3 数据归一化处理
从QAR中提取的数据是真实飞行数据,这些数据的数量级往往差异较大,这会对神经网络的训练造成一定影响:数量级较大的数据对网络连接权值影响大,数量级较小的数据对权值影响小,但是数量级的大小无法表征参数的重要程度。例如,飞行高度H的数量级可达103,而亚音速飞行的民航客机飞行马赫数Ma一直小于1,因此,需要对从QAR中提取的原始数据进行归一化处理。对数据进行归一化处理以后,数据的变化范围较小,在梯度计算过程中能显著加速梯度下降求最优解的过程。
除了能够显著加速梯度下降求最优解的过程,归一化处理还可能提高计算精度。一些分类器(例如K近邻算法)在计算样本距离时,若一个特征向量值域范围相差非常大且没有进行归一化处理,计算时值范围更大的特征向量对距离的影响更大,而K近邻算法的实际情况是,取值范围较小的特征向量对样本距离影响更大,与之相悖。在此种情况下,精度会受到影响。
常见的归一化类型有:线性归一化、标准差标准化、非线性归一化。本文选取的归一化方式是线性归一化,对原始数据进行线性归一化处理以后,原始训练数据会压缩在[-1,1]区间内。线性归一化公式为
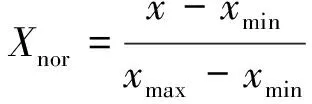
(1)
式(1)中:xmin为数据中的最小值;xmax为数据中的最大值;Xnor为数据归一化以后的输出值。
2 循环神经网络的搭建与预测模型建立
2.1 RNN网络概述
简单神经网络往往只能单独处理离散输入,即两个输入前后毫无关联,但在某些任务中需要能够更好地处理前后输入相互影响、相互关联的序列信息。循环神经网络 (recurrent neural network,RNN)是众多的人工神经网络中可以刻画序列输出与之前信息的关系的网络之一。在网络结构层面,循环神经网络能“记忆”历史数据信息,并利用已知的时间序列数据影响后面结点的输出。其实现方式为:网络隐藏层之间的结点在时间链条上按照时序相互连结,某一时刻隐藏层的输入不仅来源于该时刻输入层的输入信息,还来源于上一时刻隐藏层的输出信息。
循环神经网络是考虑了数据在时序上前后关系的一种神经网络,是一种序列——序列模型。由于其隐层是一种类似于循环链式的结构,它的每个输出除了受当前输入的影响,还受到之前输入的影响,使得数据可以持久地在网络中传播,因此,循环神经网络在时序数据处理领域具有较大的优势。图4为一个典型RNN结构图的展开形式,U为输入层权重矩阵,V为输出层权重矩阵,W为隐藏层权重矩阵。网络的输入通常是一个序列,序列中的每一个向量都会进入一个相同的胞体进行运算,得到一个状态向量(state),上一时刻的状态向量连同当前时刻的序列向量共同输入到下一个细胞中,如此循环往复。

图4 RNN按时间展开Fig.4 RNN is expanded in time
RNN结构通常用于序列问题,其数学表达式为

(2)
这个网络在t时刻接收到输入xt之后,隐藏层的值是st,相当于每次有了前面时刻的记忆,输出值是ot。值得注意的是,st的值不仅仅取决于xt,还取决于st-1。
为了衡量模型的误差与精度,需要对模型进行定量评估。引入均方误差 (mean square error,MSE)函数,MSE是一种常用的损失函数,广泛运用于回归问题,可用来检测模型预测值和真实值之间的偏差。
训练集为
Train={(x1,y1),(x2,y2),…,(xN,yN)}
(3)
测试集为
Test={(x1,y1),(x2,y2),…,(xM,yM)}
(4)
式中:N为训练样本的总数;M为测试样本的总数。若训练模型函数为f(x),此模型的输出值(即预测值)为
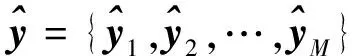
(5)
均方误差计算公式为
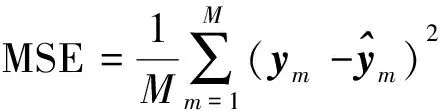
(6)
使用MSE值刻画预测值与真实值之间的差异,MSE值越大,表明预测值和真实值之间的偏差越大,预测效果也就越差。
2.2 BPTT算法训练RNN网络[15]
BPTT算法训练RNN的主要过程如下。
(1)前向传播过程计算所有神经元的输出值。
(2)反向传播计算所有神经元的误差项值(即误差函数对加权输入的偏导数)。
(3)计算每个权重的梯度,最后再用梯度下降方法或优化算法寻找使得损失函数取得最小值的梯度方向,更新权重。
假设Lt=Lt(ot,yt)作为模型的损失函数,为了更清晰地表明网络配置,将RNN网络展开成如图5所示的结构。

图5 网络配置结构Fig.5 Network configuration structure
根据网络结构可知,对矩阵V的求导过程和输出过程即为普通的反向传播算法,用公式表示为

(7)
由式(7)可以看出,梯度除了按照空间结构传播ot→st→xt以外,还得沿着时间通道传播st→st-1→…→s1。
由于 RNN 需要沿时间通道进行反向传播,若选取在某个时间步长内求解梯度,其相应的“局部梯度”为

(8)
BPTT和BP算法的本质区别是:RNN有记忆历史数据信息的功能,它的输出不仅仅依赖于输入数据,而是当前输入和该时刻的记忆共同运算的结果。RNN的记忆有序列——序列的特点,即当前时刻的输出受到上一时刻的影响。因此,使用BPTT算法训练RNN时,若在当前时刻对参数进行求导运算,一定会涉及前一时刻。
2.3 Adam优化算法[15]
优化算法的任务是在每一个epoch中计算损失函数的梯度,进而更新参数,从而使损失函数快速准确逼近最小值。优化算法的通用框架如下。
定义待优化参数ω,损失函数f(ω),初始学习率α,每次迭代一个batch,t表示当前batch迭代的总次数。更新步骤如下。
(1)计算损失函数关于当前参数的梯度,即

(9)
(2)根据已知历史梯度计算一阶动量和二阶动量,即

(10)
(3)计算当前时刻的下降梯度,即
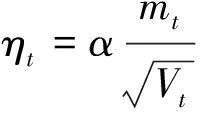
(11)
(4)根据下降梯度进行更新,即
ωt+1=ωt-ηt
(12)
Adam优化算法结合了SGDM和RMSProp优化算法的优点,把SGDM的一阶动量和RMSProp的二阶动量结合起来,再修正偏差。
SGDM的一阶动量计算式为
mt=β1mt-1+(1-β1)gt
(13)
加上RMSProp的二阶动量计算式为
Vt=β2Vt-1+(1-β2)gt2
(14)
式中:参数经验值是β1=0.9,β2=0.999。
初始化m0=0、V0=0,在初期,迭代得到的mt、Vt会接近于0。可以通过对mt、Vt进行偏差修正来解决这一问题,即

(15)
Adam优化算法主要包含以下几个显著的优点:很适合应用于数据和参数规模极大的场景;更新的步长能够被限制在大致的范围内;能自动调整学习率;适用于梯度稀疏或梯度存在很大噪声的问题[16]。
2.4 超参数选取
模型最重要的超参数之一是学习率LR,其经验值通常选择为0.01~0.001。学习率越小越容易拟合,但是学习更新相对较慢;若学习率较大,参数的迭代更新越快,但同时输出误差在反向传播过程中对参数的影响会增大,若训练数据包含异常数据,对训练结果的影响也会随之增大,最终容易引起发散的结果,本次实验选择学习率为LR=0.001。每次喂入网络的数据个数BATCH_SIZE(批尺寸)越大,其确定的下降方向是梯度下降方向的概率越大,由训练引起的震荡也越小,批尺寸过大会过多占用计算机内存,综合考虑,BATCH_SIZE 设置为256。其他几个重要超参数由以下调整实验产生。
2.4.1 Seq调整实验
参数时序长度Seq的含义是:RNN网络利用前Seq个历史数据信息和当前输入值预测当前时刻的输出值。为了获得Seq的最佳值,在固定epoch=10,学习率LR=0.001的情况下,进行Seq调整实验。部分损失函数曲线与某航班的预测曲线如图6所示。

图6 Seq调整实验Fig.6 Seq adjustment experiment
调整实验中涉及的所有Seq值相应的训练和测试损失值变化如表1所示。
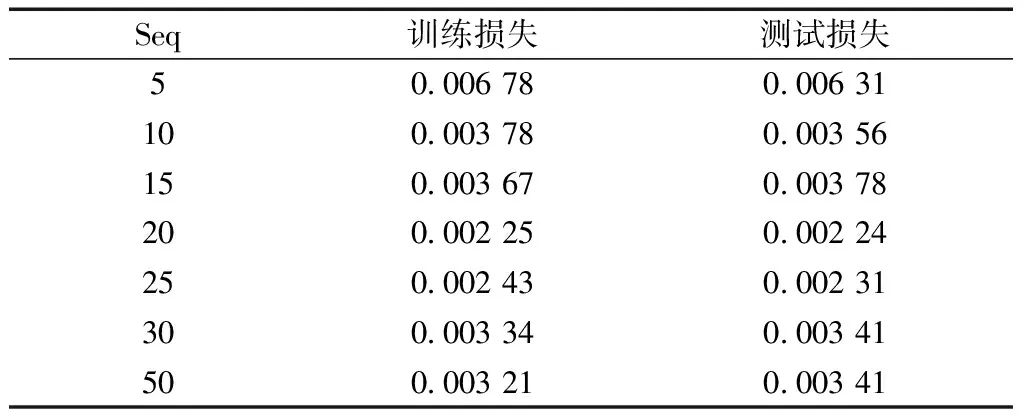
表1 Seq调整实验损失值变化汇总
实验结果显示,在Seq=20时训练损失函数与测试损失函数MSE值都取得较小值,数据拟合也较好,故将Seq设置为20。
2.4.2 epoch调整实验
在设置Seq=20,学习率LR=0.001的情况下,进行epoch调整实验。实验结果如图7所示。
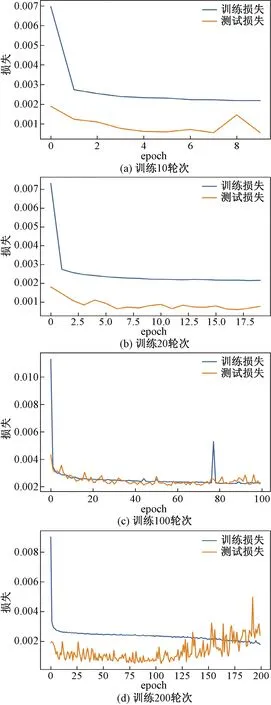
图7 Epoch调整实验Fig.7 Epoch adjustment experiment
结果显示,在epoch<100时,训练集和测试集数据都在逐渐缓慢降低,在epoch>100后,测试集数据的MSE值出现了震荡甚至上升。综合考虑计算机算力、误差衰减等情况,将epoch值设置在100较为合适。
2.5 建立燃油流量预测模型
2.5.1 数据还原曲线
为了使样本更具代表性,表征大部分航班预测情况,根据QAR数据将航班划分为短航程、中远航程和远航程航班进行分类预测,划分主要依据是时间和数据点,数据点小于 7 000 以下的划分为短程航班,7 000~10 800 划分为中远程航班,10 800 以上的划分为远程航班。现对建立的燃油流量预测模型分别进行短航程、中远航程和远航程预测对比,以评判预测模型对其原数据的还原度,模型的训练数据损失值MSE=0.002 51,训练数据还原结果如图8所示。
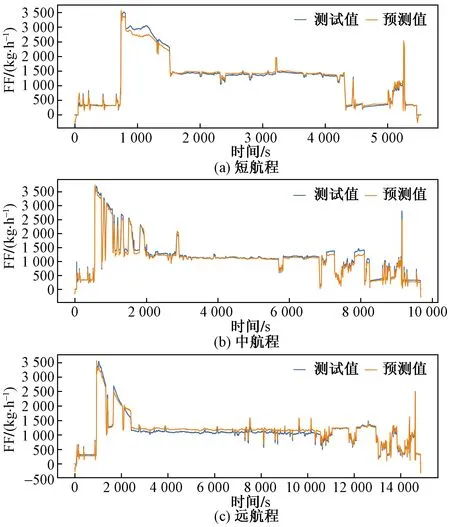
图8 短、中、远航程训练用数据还原度Fig.8 Training flight data fitting result in short、medium and long range respectively
可以看出,对于短程航班,模型只在飞机燃油流量突变时拟合效果不佳,整体拟合效果良好。
对于中远程航班,只有起飞前以及流量连续变化等复杂工况时有少许偏差,模型整体拟合效果良好。
对于远程航班,在巡航阶段有较长时间数据与实际值存在较大偏离,数据还原效果欠佳。
2.5.2 燃油流量预测曲线
为了保证预测模型的可用性,用真实的三个不同航程的航班进行预测模型预测值与真实的燃油流量进行对比分析。模型在测试数据上的MSE值为0.001 36,测试数据预测结果如图9所示。
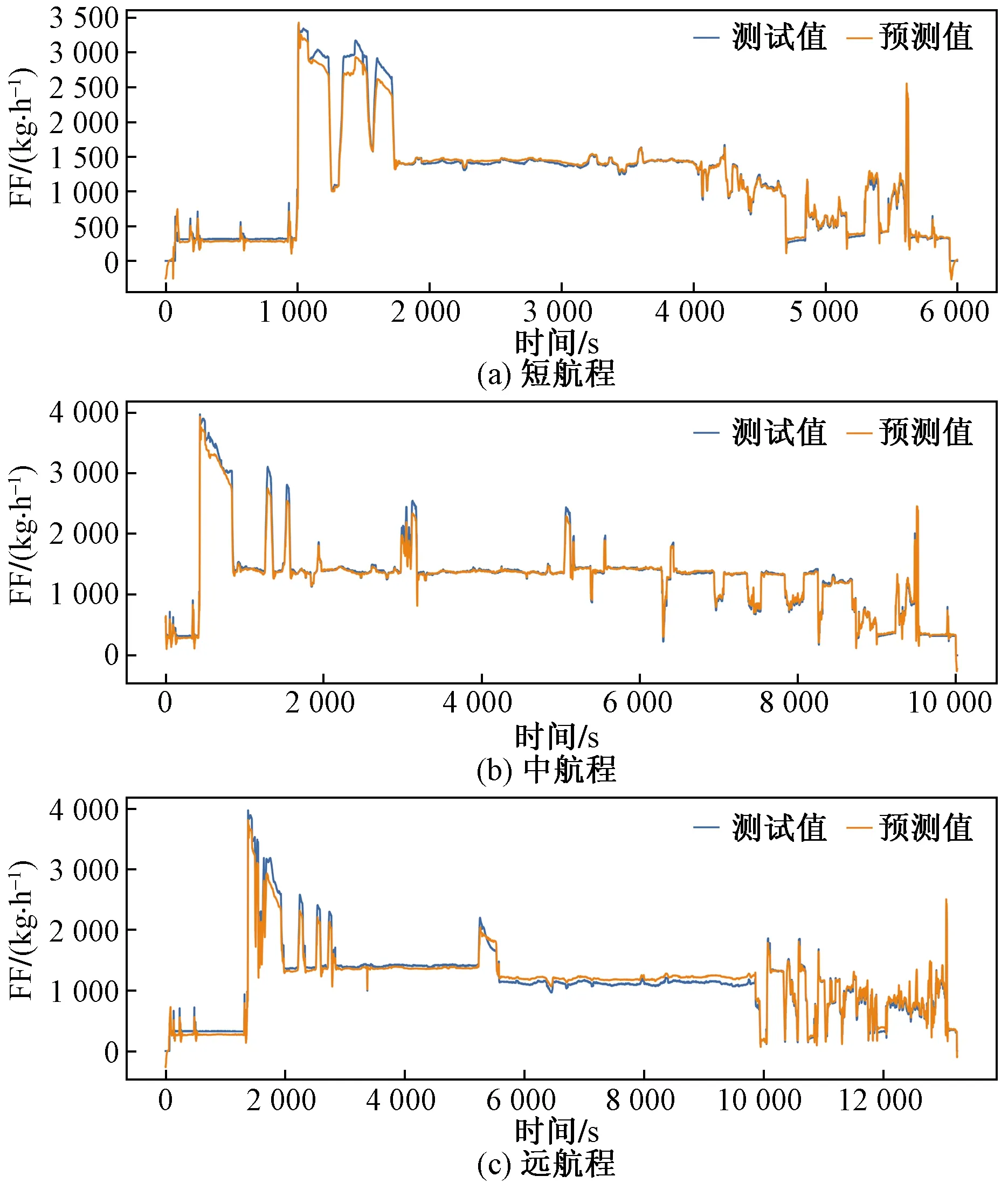
图9 短、中、远航程预测结果对比Fig.9 Comparison among short、medium and long range prediction results
可以看出,对于短程、中远程航班,模型只在飞机燃油流量有较大突变时预测值与实际值有较大偏移,整体预测效果较好。
对于中远程航班,模型整体预测效果较好。
对于远程航班,在巡航阶段较长一段时间内,预测值较大偏离实际值。
2.6 预测结果分析
结合训练历史数据和分析对比预测结果曲线图可知,当飞机遭遇燃油流量在短时间内急剧变化的复杂工况时,预测结果误差相对较大,除了在复杂工况和起飞前易出现个别偏差较大的数据点外,其他飞行阶段的预测值相对较为稳定。相对于短航程和中远航程航班,远航程航班在训练数据的巡航阶段拟合结果偏差较大,其他阶段预测结果较为稳定。
2.7 梯度消失与梯度爆炸
结合表3中Seq调整实验的实验结果,随着Seq值的增加,训练数据与测试数据上的损失函数先减小后增大,一个可能的原因是:RNN在初期发挥了它能记忆历史的信息的优点,随着Seq增大,网络记忆的信息增多,从而获得越来越好的预测效果,训练数据和测试数据上的损失值也减小;当Seq值增大到某一个临界值时,在BPTT算法执行的过程中,产生了梯度消失或梯度爆炸等问题,模型的预测能力减弱,损失值也随之增大。
3 引入GRU重构预测模型
3.1 门控循环单元GRU内部结构
门控循环单元(gate recurrent unit,GRU)是循环神经网络的一种改进形式,相较于朴素神经网络,GRU引入了门控单元,很好地解决了循环神经网络中极易发生的长期记忆力不足,反向传播中梯度消失、梯度爆炸等问题。GRU的输入输出结构与朴素RNN类似,一个典型的GRU输入输出结构如图10所示。

图10 GRU的输入输出结构Fig.10 GRU’s input and output structure
其基本工作逻辑是:先通过上一个传输下来的状态ht-1和当前节点的输入x来获取重置门r和更新门z两个门控状态,其表达式为

(16)

(17)
得到相关信号之后,重置门控r首先发挥作用:使用重置门控r来得到“重置”之后的数据h′t-1,运算过程为:h′t-1=ht-1⊙r。再将h′t-1与输入xt进行组合拼接,随后将拼接数据通过一个tanh激活函数将数据放缩到[-1,1]的范围内,即得
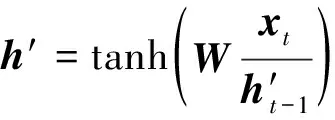
(18)
式(18)中:h′包含了当前输入的xt数据,相当于“记忆”了当前时刻输入信息的状态。随后是“更新记忆”阶段。在这个阶段,同时进行遗忘和记忆两个步骤。更新表达式为
ht=z⊙ht-1+(1-z)⊙h′
(19)
式(19)中:门控信号z的范围为0~1,其表征记忆能力的大小。z越接近1,意味着记忆的数据越多;而z越接近0,则代表遗忘的数据越多。GRU内部结构及其工作流程示意图如图11所示。
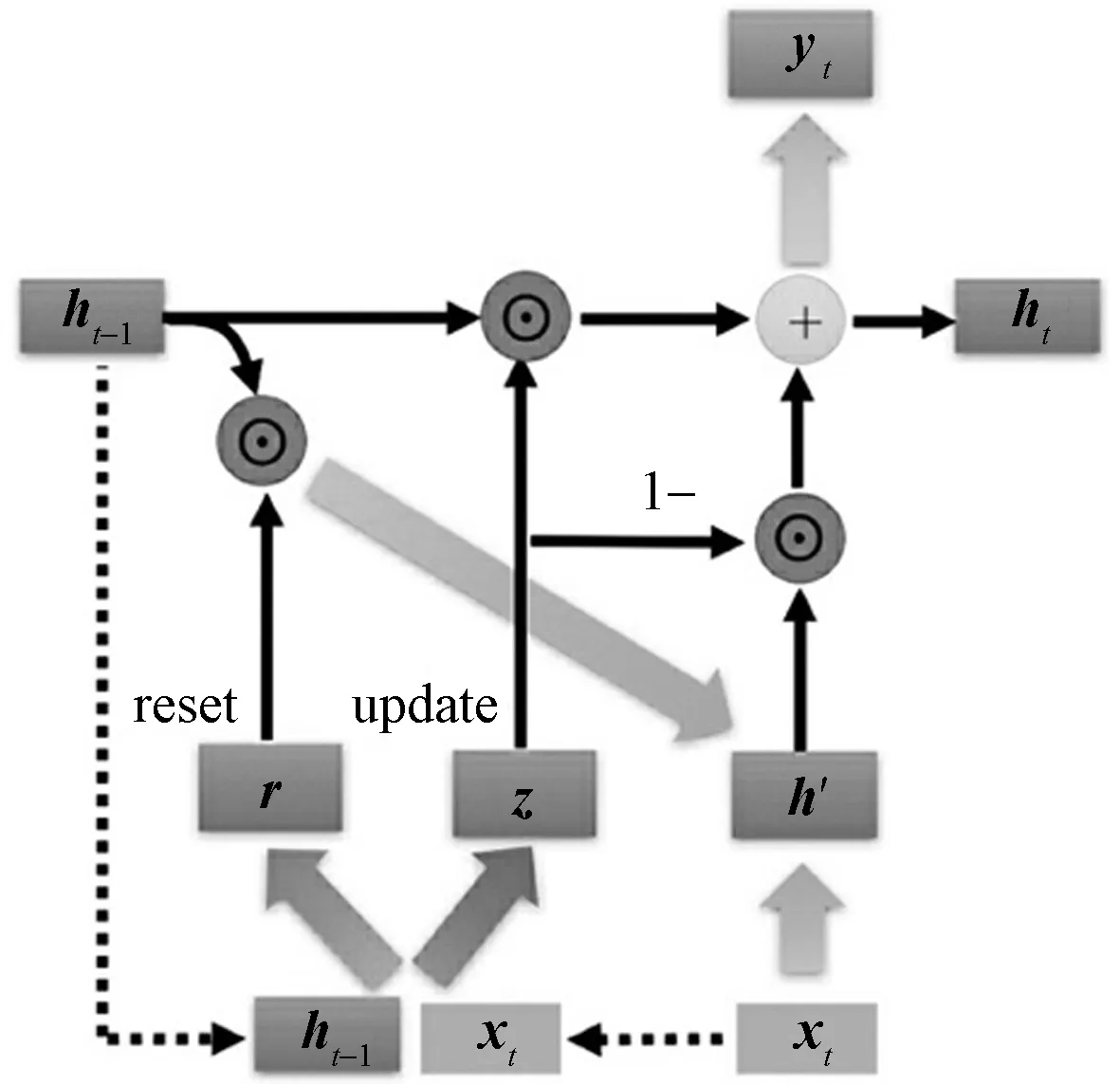
图11 GRU的内部结构Fig.11 GRU’s internal structure
GRU的反向传播过程与RNN相同,相比于RNN的梯度下降是单项式连乘,GRU则是多项式相乘,因此GRU更难发生梯度消失。
3.2 使用GRU改进预测模型
为了与朴素RNN网络进行对比,设置超参数LR=0.001, Seq=20, epoch=100, BATCH_SIZE=256,使用与朴素RNN网络相同数据集对改进后的网络进行训练,在经过100轮迭代后,其损失函数MSE值在训练集和测试集上分别为0.002 03、0.000 98。可以看出,在相同的参数条件下,改进后的模型损失值相较于原始模型损失值只有微小改变。可能的原因是,使用相同的参数限制了GRU网络的工作能力,GRU网络的一个特点就是:能够记忆更多的信息,使用现有参数限制了GRU网络记忆。
对GRU网络进行一系列Seq调整实验与epoch调整实验,找到该网络较好的参数为LR=0.001,Seq=40,epoch=10。改网络的损失函数MSE值在训练集和测试集上分别为0.001 08、0.000 97, 训练集和测试集上损失函数变化如图12所示。短程、中远程、远程航班的预测曲线分别如图13所示。
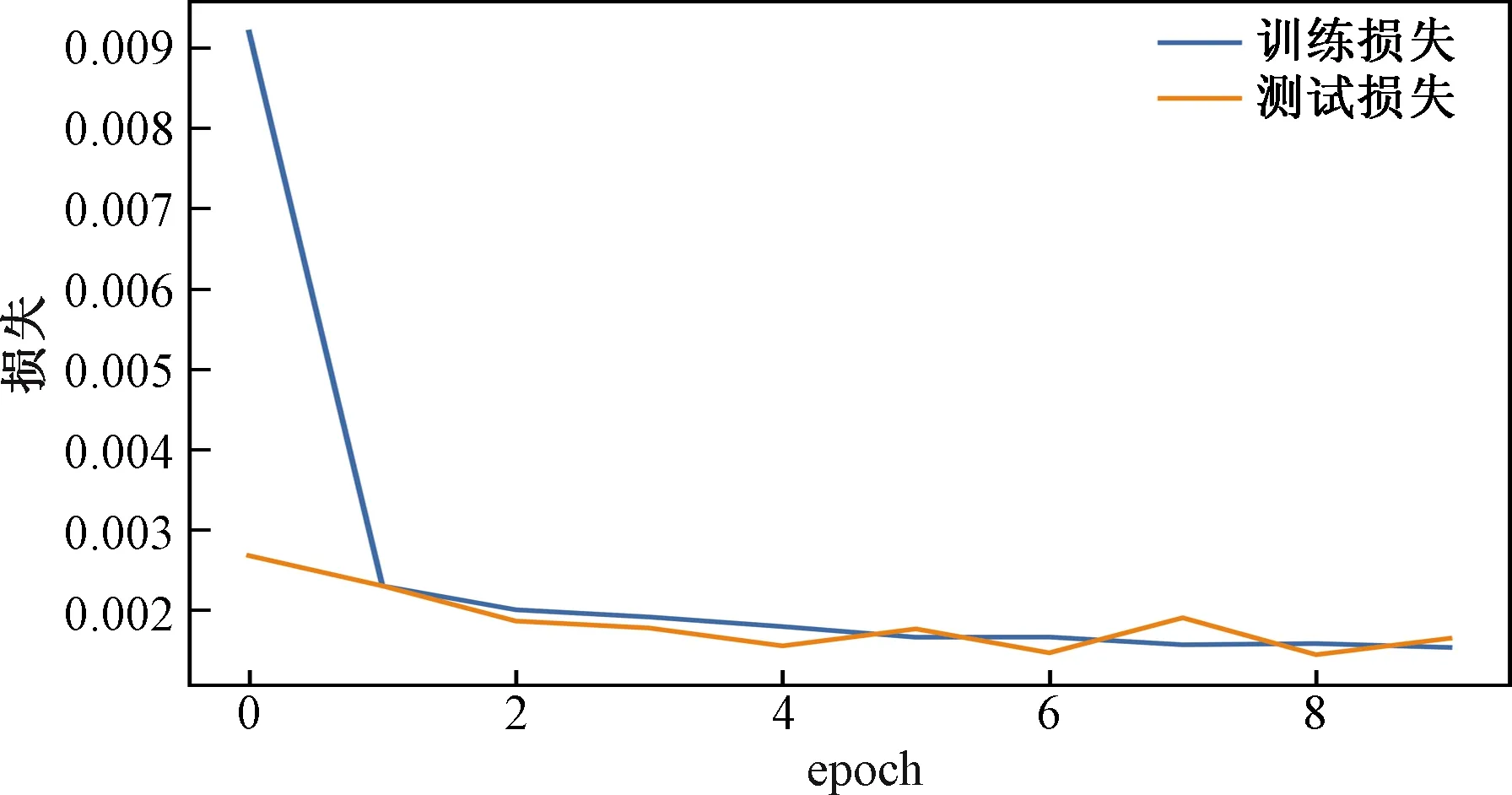
图12 GRU网络损失函数变化Fig.12 Change of loss function of GRU network
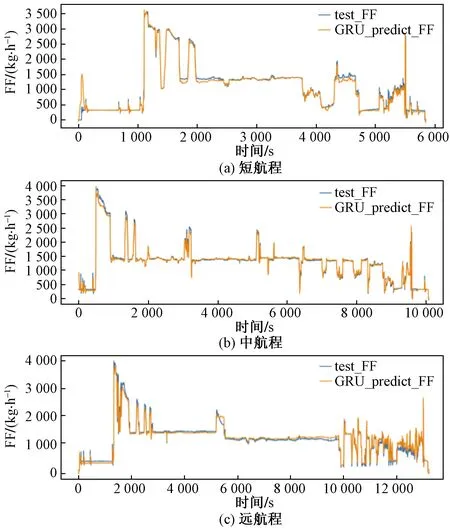
图13 短、中、远航程GRU预测结果Fig.13 GRU prediction results in short、 medium and long range respectively
与RNN预测曲线对比可知,GRU预测曲线在燃油流量突变处预测效果有了明显改善。
对于中远航程航班,不管是起飞前流量突变处还是巡航阶段预测值与真实值偏差均较小,整体预测效果较好。
对于远程航班,GRU显著改善了朴素RNN在巡航阶段预测效果差的问题,整体预测效果很好。
3.3 预测结果对比
表2为在相同超参数条件下(LR=0.001,Seq=20,epoch=100, BATCH_SIZE=256),朴素RNN和改进GRU网络的损失函数MSE值的对比结果。表3展示了在各自最优超参数条件下(RNN参数为LR=0.001,Seq=20,epoch=100, BATCH_SIZE=256,GRU参数为LR=0.001,Seq=40,epoch=10, BATCH_SIZE=256)使用朴素RNN和改进GRU网络所建立的预测模型在训练集和测试集上的MSE值。结果显示,改进后的GRU网络在训练轮次少于朴素RNN网络的情况下,其训练误差和测试误差均明显减小,短程、中远程、远程航班的预测曲线拟合效果也更佳,对于朴素RNN网络在远程航班的预测曲线拟合效果不佳的问题也有了明显改善。由此可见,使用GRU结构的模型显著改善了模型的预测能力,有较好的预测效果。

表2 相同超参数预测结果对比

表3 各自最优超参数预测结果对比
3.4 故障模拟与分析
本文中所建立的燃油流量预测模型除了可以用于预测飞机燃油消耗,也可用于故障预测与分析。若飞机在实际运行中出现了故障(如传感器故障、系统故障等),导致相关的QAR数据出现异常值,此时预测曲线和原始数据曲线会出现较大偏差,训练得到的损失函数MSE值也会大于原始模型MSE值。由于本次研究建立的模型涉及的相关参数较少,出现偏差后可以根据这些数据产生的部件快速锁定故障后排故,能极大减少故障诊断时间。
根据故障隔离手册(fault isolation manuel,FIM)手册进行故障模拟与分析。模拟的故障为:从第6 000秒开始,某一与监控燃油流量相关的传感器线路异常而使QAR数据记录器记录的燃油流量数值异常,直到第8 000秒传感器恢复到正常状态该故障才被解除。该异常状态是由于线路异常引起的数据异常问题,其他与模型相关的参数均为正常状态。从图14模拟故障预测对比曲线可以看出,预测值与测试值出现了极大偏差,此时模型在训练数据上的损失函数MSE值整体提升到了0.001 69,远大于模型初始的MSE值0.000 97,由此可以断定故障出现,技术人员可以根据技术手册快速在相应章节展开故障调查。
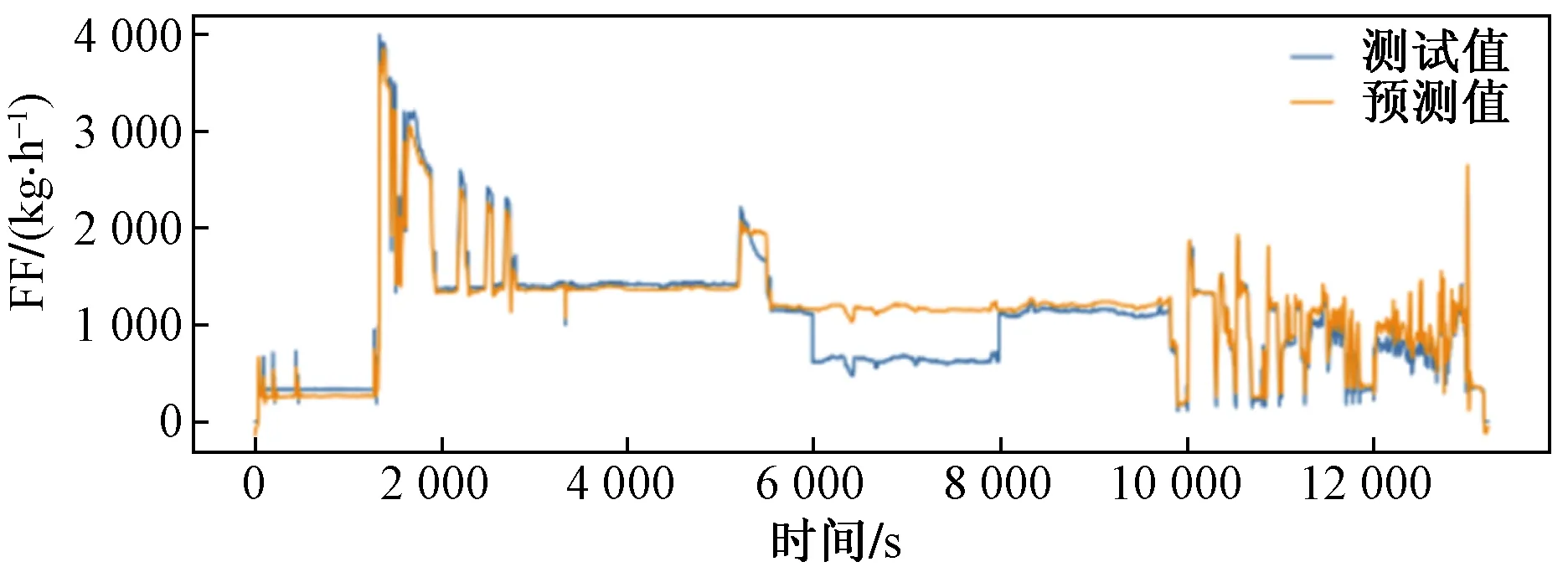
图14 模拟故障预测对比曲线Fig.14 Simulation fault prediction comparison curve
对曲线做进一步分析,预测值大致维持在正常状态,而原始数据曲线出现了极大波动且数据全部偏小,这表征了与预测模型相关的参数未出现较大变化,导致这一现象的原因可能是:QAR(3TU)接头异常,或者相关传感器线路异常,技术人员可以根据对该异常的分析和调取相应时间段的飞行数据快速锁定故障部位,极大减少故障诊断时间。
4 结论
循环神经网络具有记忆历史信息的能力,对时间序列研究有较好的适用性,善于对变化较大、影响因素多的时间序列数据进行拟合,因此,本文所建立的燃油流量预测模型拟合效果较好。
本文研究主要步骤为:首先根据统计学分析和发动机控制原理选择主控参数:TRA、H、Ma、TAT、N1、N2。对这些数据进行小波去燥、归一化处理后,搭建朴素RNN网络,构建燃油流量预测模型,在参数调整实验中发现循环神经网络对历史信息利用能力不足,遂提出改进网络结构,引入门控循环单元(GRU)重构预测模型。
与朴素RNN和GRU构建的燃油流量预测模型在相同数据上的预测结果对比曲线,其在各自的最优超参数条件下,在测试集上的损失函数MSE值分别为0.001 36、0.000 97,通过对比曲线和误差值的对比可以发现,改进后的网络结构的预测精度与拟合能力显著提高。且改进后的网络在训练轮次远小于原始网络情况下预测表现仍更佳,这极大节省了计算机算力。
改进后的GRU网络能够“记忆”更多历史信息而不会出现梯度消失或梯度爆炸等问题,针对朴素RNN网络在远程航班的预测曲线拟合效果不佳的问题也有了明显改善。由此可见,使用GRU结构的模型显著改善了模型的预测能力,有较好的预测效果,且具有很强的可靠性,可以利用该预测模型进行故障诊断等实际应用。
