木鱼包滑坡变形与库水位相关性定量化分析
2021-10-15周永健冯文凯易小宇肖锐铧
周永健, 冯文凯*, 易小宇, 孟 睿, 肖锐铧
(1.成都理工大学地质灾害防治与地质环境保护国家重点实验室, 成都 610059; 2.四川省国土空间生态修复与 地质灾害防治研究院, 成都 6100813; 3.中国地质环境监测院, 北京 100081)
滑坡是水库常见的地质灾害之一[1],库区发生滑坡不仅会影响库区的正常运行,还可能造成重大的人员伤亡。1963年意大利瓦依昂水库的失事就造成了约2 000人死亡[2-3],在经历了这次惨痛的教训之后,人们开始意识到了水库滑坡的严重性。三峡库区自2003年蓄水以来,库水位在 145~175 m之间周期性的大幅度变动改变了库区原本的地质环境,导致库区两岸发生了大量的滑坡。据统计,三峡库区内已发现的滑坡与潜在滑坡的数量已经超过5 000多个[4-5],三峡库区的木鱼包滑坡作为受到库水位波动影响而出现变形加剧的典型例子,受到了许多关注。周剑等[6]对三峡木鱼包滑坡15年进行了分析,并结合数值模拟发现木鱼包的变形与随着库水位的变化呈现规律性变化。李永康等[7]以白家包滑坡为例,分析了不同渗透系数、不同库水位升降速率下的滑坡稳定性,认为库水位升降时,水土作用会导致浮托减重效应的产生,但而浮托减重效应小于动水压力作用。冯文凯等[8]通过离心模型试验探究了木鱼包滑坡的变形对库水位升降的响应,试验结果表明库水升高时的浮托力控制着滑坡的变形。
以上学者主要是通过物理模型试验结合数值模拟研究了滑坡变形的影响因素,而使用定量计算对滑坡影响因素进行相关性分析的研究还较少。与有长期监测数据的木鱼包滑坡,通过计算监测数据之间的相关性来分析影响滑坡变形的影响因素,往往比物理模拟与数值模拟方便简单。因此,现从对木鱼包滑坡多年的变形监测数据与库水位数据、降雨量数据的对比分析入手,采用相关性计算分析的方法,确定不同时间尺度下的数据(位移量、水位高程、降雨量)之间的斯皮尔曼相关系数,判断木鱼包滑坡的变形情况与库水位高程、降雨量之间的相关性,进而确定库水位高程和降雨量对木鱼包滑坡的影响。
1 木鱼包滑坡概况
1.1 工程地质条件
木鱼包滑坡地处中国湖北省秭归县,长江右岸,距三峡大坝约56 km。滑坡前缘剪出口的高程约100 m(现已没入水下),后缘高程约520 m,两侧以沟谷为界。滑坡在平面上形似马蹄(图1),滑体均宽1 200 m,纵长1 500 m,面积180×104m2,平均厚度50 m,体积约9 000×104m3,为一特大型的岩质古滑坡,该滑坡一旦成灾,将会危及滑坡区内140户500多位村民的生命财产安全,并影响长江的航运安全。
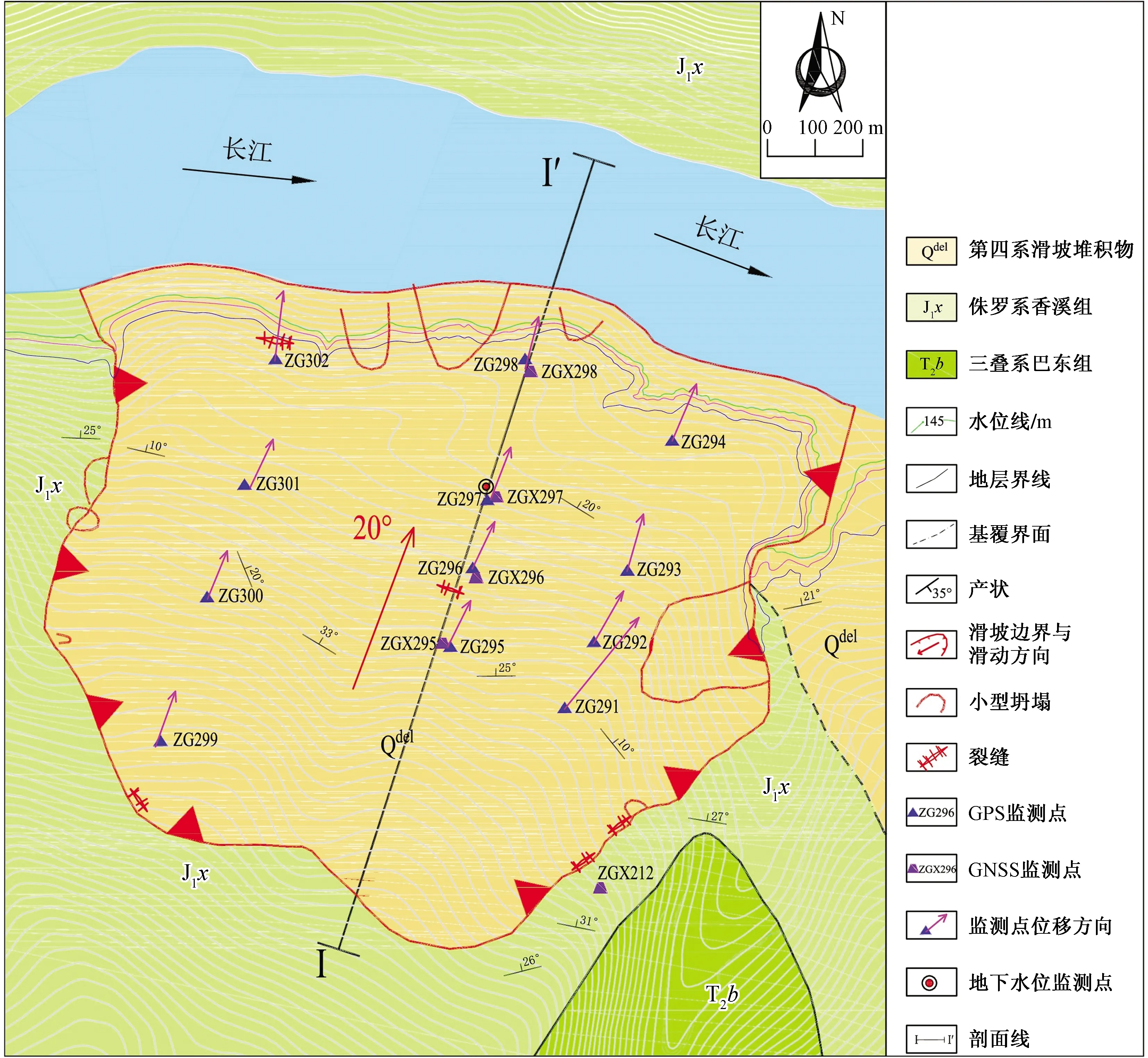
图1 木鱼包滑坡工程地质平面图Fig.1 Geomorphological map of the Muyubao Landslide
1.2 表面变形监测结果
位移监测数据来源于三峡大学在滑坡体内布置的12个GPS(global positioning system)和4个GNSS(global navigation satellite system)位移监测装置,监测点的布置见图1。降雨数据与库水位高程数据则是分别从附近的雨量站和三峡公司的网站获取的,文中使用的位移数据均为水平位移数据。
图2(a)为GPS位移监测点从2007—2017年的水平位移累计曲线,为便于阅读,根据曲线的变化幅度将曲线分为三类进行了标注。从图中可以看出监测点GZ291的累计位移曲线明显高于其他监测点的累计位移曲线,并且随着时间的推移,监测点GZ291的累积位移与其他监测点累积位移的差值越来越大。通过现场调查,发现监测点GZ291所在的山脊存在向东侧冲沟的变形,从而导致监测点GZ291的累计位移大于其他监测点。
除监测点GZ291之外,其余11个GPS监测点的水平位移累计曲线几乎保持着一致的变化趋势, 直到2017年12月,11个位移监测点的水平累计位移至都介于1 300~1 665 mm,并且水平位移的方向基本指向长江(11°~45°)。总体上来看,木鱼包滑坡的累积位移曲线呈现出逐年增加的趋势,并且还体现出“阶跃”上升的特点。“阶跃”现象的出现说明木鱼包滑坡的变形存在有加速变形的情况。
图2(b)为2010—2012年期间累积位移曲线,曲线呈现出周期性变化的特点,根据形变速率的大小与增减情况,文中将一个周期内的曲线划分为等速上升阶段、加速上升阶段以及减速上升阶段,这3个阶段分别对应着滑坡的等速变形阶段、加速变形阶段以及减速变形阶段。
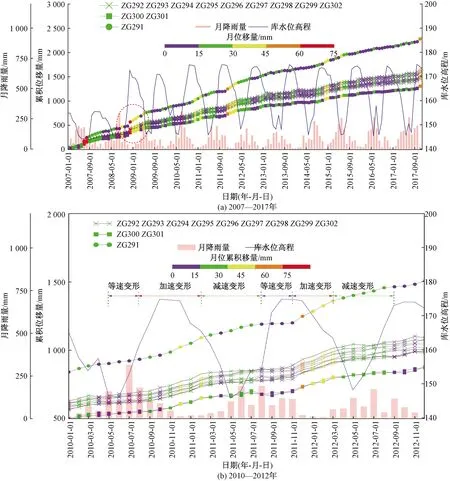
图2 GPS监测点累积与库水位、降雨量关系曲线Fig.2 Cumulative displacement of GPS monitoring points and its relationship with reservoir water level and rainfall
在库水位较低时,月累计位移量低于15 mm,位移累积曲线处于等速上升阶段,累积曲线缓慢上升;随着水位的升高,月累计位移超过15 mm并持续增加时,累计曲线进入加速上升期,累计曲线上升速度加快;在水位从最高点降低一段时间后,监测点变形速率开始降低,在月累积位移量降低至15 mm之前为减速上升阶段,当监测点的月累积变形量减小至15 mm时,减速上升期结束,开始下一周期的等速上升期。
2 影响因素的定性分析
从图2(a)中可以看出,每年随着水位高程的增加,几乎各个监测点的变形速率都会增加,这一现象在库水第一次上升的过程中最为明显[图2(a)中的红圈]。2008年水位第一次从145.9 m快速上升至172.6 m的过程中,监测点的变形速率几乎随着库水的上升同步增加,累积变形量从水位上升之前的每月不足15 mm增大到30 mm以上,其中最大超过了80 mm,之后又随着库水位的下降而开始减慢,最后减小至每月15 mm以下。水库在之后多年的运行中,这一现象伴随着水位的变化为而周期性出现,尽管变形速率的增大没有2008年的明显,但是依旧能够明显看出变形速率随着水库增加而增加,而与2008年不同的是滑坡变形速率的增加并非是与水位的上升过程同步,而是存在一定的滞后期。
图3反映了2007—2017年GPS监测点的月累计位移量与库水位高程以及月降雨量之间的关系。从图3中可以看出,在水位高程高于160 m但月降雨量不足40 mm的旱季有大量GPS监测点月累计位移量超过30 mm的事件发生(紫色虚线方框),其中2008年水位上升至175 m附近时的月累积位移量最大,所有监测点的累积位移量都大于50 mm(红色虚线方框),并且有部分监测点的月累积位移量超过了80 mm。另一方面,在库水位高程比较低的雨季,某些时段的月降雨量超过了200 mm,但月累计位移量却不足30 mm。综上所述,本文初步判断库水位高程的增加是导致木鱼包滑坡产生加速变形的主要原因,而降雨量对木鱼包滑坡变形影响并不明显。
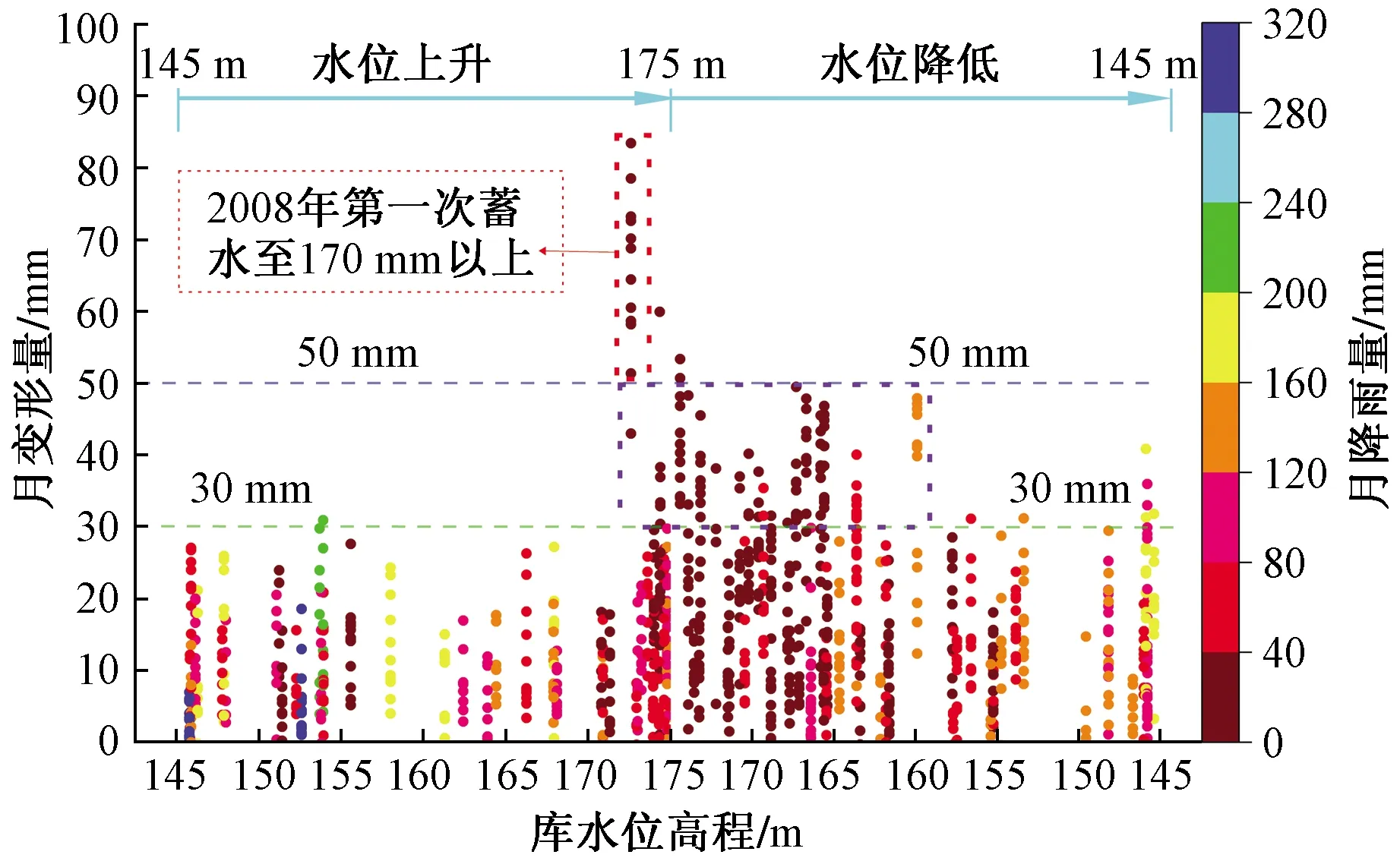
图3 月累积位移与库水位高程、月降雨量关系图Fig.3 The relationship between monthly displacement and water level and rainfall
3 影响因素的定量计算分析
为了进一步确定水位高程和降雨量对木鱼包滑坡的影响,本节将借助相关性分析,计算不同时间尺度下的监测数据(滑坡位移量与库水位高程、降雨量)之间的相关性。大时间尺度的数据为2008—2017年的每月监测数据,而小时间尺度的数据为2016—2018年的每日监测数据。
3.1 相关性分析原理
相关性分析是指对两个或是多个变量元素进行相关性检验,根据计算结果来衡量变量之间的相关程度与相关方向的分析方法。在相关性分析中,皮尔逊相关系数与斯皮尔曼相关系数常用于衡量两个变量之间的相关程度以及相关方向。其中计算皮尔逊相关系数时要求变量之间为线性相关且为二元正态分布,而本文中的水位高程数据不满足于正态分布,因此本文选择斯皮尔曼相关系数ρ作为相关性的判断依据。斯皮尔曼相关系数是根据各个数据的排序名次进行计算得出,计算表达式[9-10]为
(1)
式(1)中:ρ为斯皮尔曼相关系数,介于-1~1,|ρ|越靠近1相关性越强,|ρ|≥0.8表示变量之间为高度相关,0.4≤|ρ|<0.6表示中度相关,0.2<|ρ|≤0.4表示弱相关性,|ρ|≤0.2表示相关性极弱;D为两个数据次序的差值;N为数据的数量。
3.2 大时间尺度数据的相关性分析
选择位于剖面线1-1上的4个监测点(GZ295、GZ296、GZ297、GZ298)的位移监测数据,并从中挑选出加速变形阶段与减速变形阶段内的月位移量作为计算变量D,以变量D之前0~5个月内的水位高程和降雨量数据作为其他变量(表1),分别计算变量D与其他变量之间的斯皮尔曼相关系数,计算结果见表2与表3。
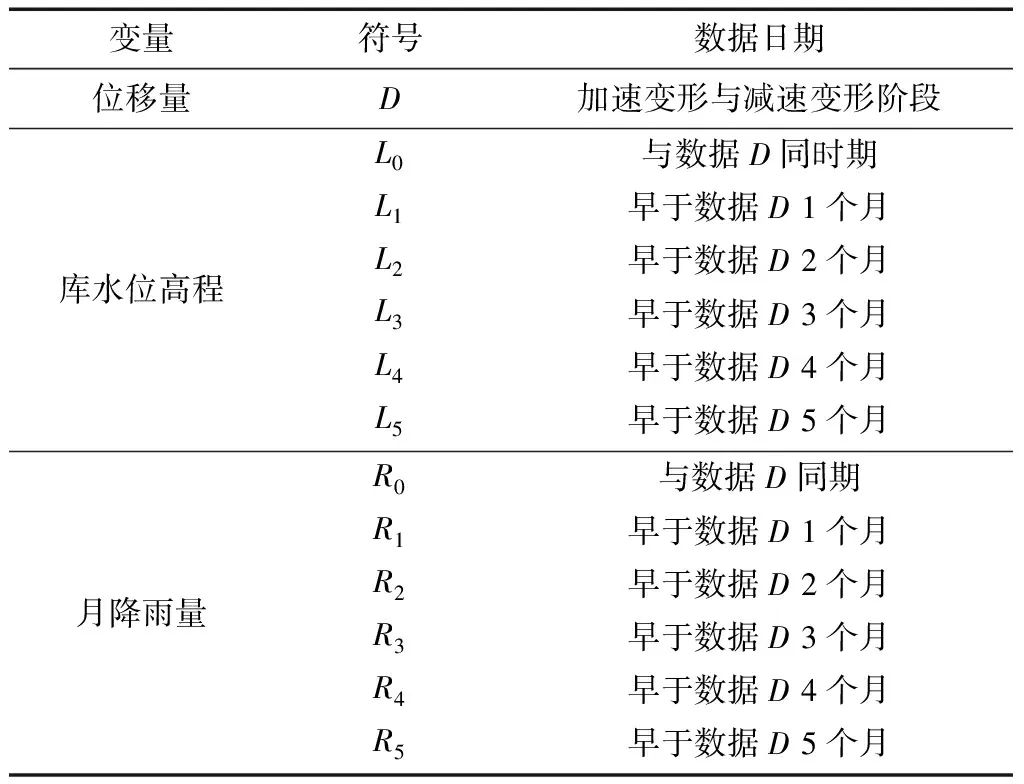
表1 相关性计算的变量Table 1 Variables for correlation calculation
表2为木鱼包滑坡的月累计位移量与水位高程之间的斯皮尔曼相关系数ρw。从表2中可以看出月累计位移量与前四组变量(L0~L3)之间的相关系数均大于0,其中第三组变量(L2)对应的斯皮尔曼相关系数的平均值最大,4个监测点的相关系数的平均值为0.41,其中2个的相关系数大于0.4,为中度正相关,另外2个约为0.38,为弱相关,并且各个相关系数相应的Sig均小于0.005。
根据相关系数平均值大于0.41且对应的Sig值小于0.005,可认为滑坡发生加速变形前3个月内的月平均水位高程数据与滑坡的月累计变形量数据之间均具有显著的正相关性,其中2个月前的月平均水位高程数据与滑坡的月累计变形量数据之间的相关系数为具有最显著的正相关性。而表3中记录的滑坡月累计位移量与月降雨量之间的斯皮尔曼相关系数ρr的绝对值大于0.2的仅有6个,并且较为分散,这说明木鱼包滑坡的变形量数据与降雨量数据之间几乎不存相关性。
根据表2与表3的结果,可以看出库水位高程与木鱼包滑坡的变形量之间存在着显著的正相关性,而降雨量与变形量之间的并无明显的相关性,表明影响木鱼包滑坡变形的主要是库水的高程,而降雨量的影响并不明显。并且滑坡的位移量与前1~2个月内的库水高程为显著正相关,说明了随着水位高程增加,滑坡的位移量增大,而水位高程降低时滑坡的位移量又逐渐减小,但是水位高程的升降与滑坡变形速率的增减并不是同步的,即滑坡变形速率增大滞后于水位高程的增加,滞后期为1~2个月。
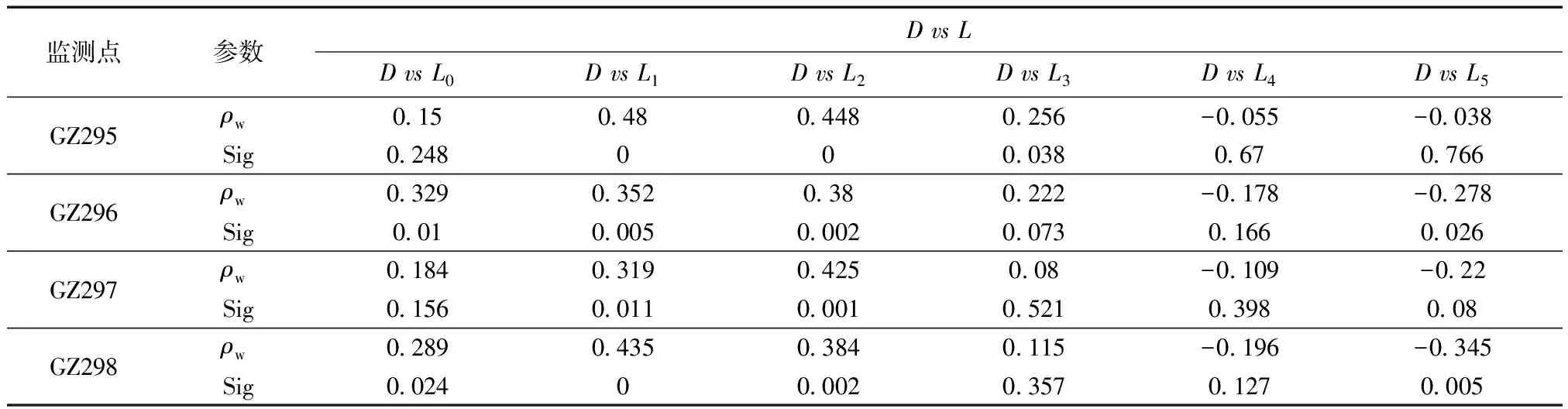
表2 累积位移量与水位高程之间的斯皮尔曼相关系数Table 2 Spearman’s rank order correlation coefficient between cumulative displacement and water level elevation
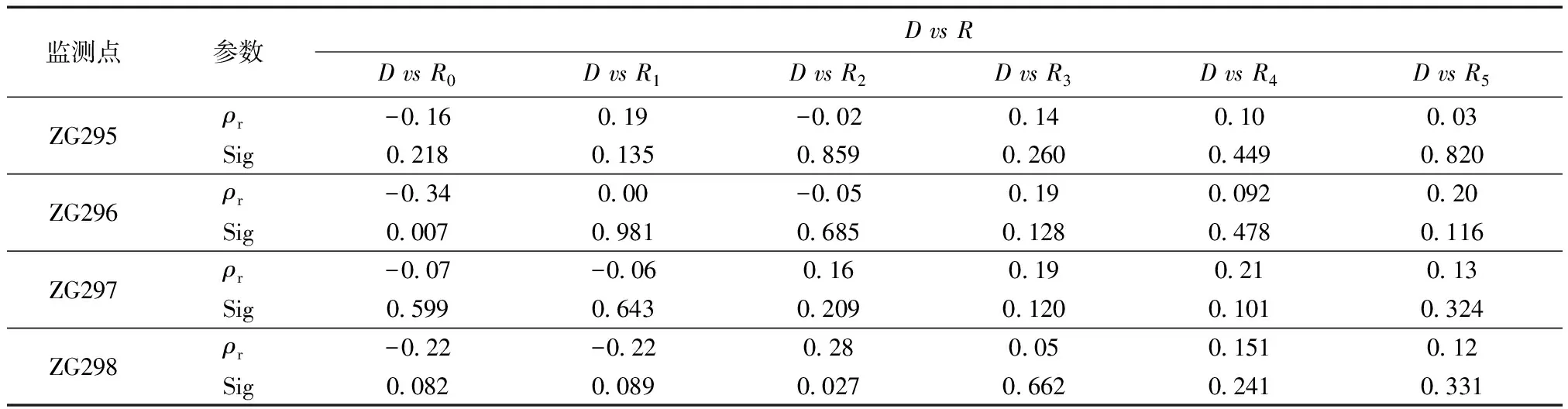
表3 累计位移量与月降雨量之间的斯皮尔曼相关系数Table 3 Spearman’s rank order correlation coefficient between cumulative displacement and rainfall
3.3 小时间尺度数据的相关性分析
图4为木鱼包滑坡从2016年5月20日—2018年3月28日的每日监测数据,数据由GNSS自动监测获取,该数据能够更加准确地反映滑坡发生加速变形与水位升高之间的滞后关系。通过对数据的筛查得知,水位从2016年9月8日开始上升后的第51天滑坡第一次开始出现变形加速;水位从2017年8月19日开始上涨后的第48天滑坡第二次出现加速变形,这说明滑坡两次发生加速变形与水位升高之间的滞后时间分别为51 d与48 d。由此能够说明对大尺度数据分析得出的结论是合理的,所使用的斯皮尔曼相关性分析方法也是可行的,但同时也说明了通过大时间尺度的数据计算得出的结果还不够精确。
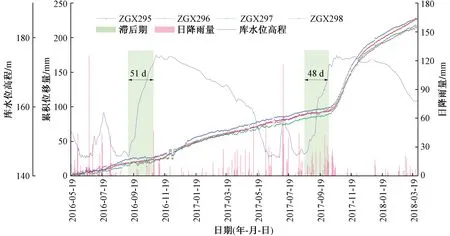
图4 GNSS监测点累积与库水位、降雨量关系曲线Fig.4 Cumulative displacement of GNSS monitoring and its relationship with reservoir water level and rainfall
现使用木鱼包滑坡2016年5月—2018年3月的每日监测数据(图4)进行相关性分析,计算木鱼包滑坡从2016年5月—2018年3月间滑坡的每日位移量与前30~60 d内的每日库水位高程之间的相关性系数,以获取更精确的滞后期,计算结果如表4。
从表4中显然看出之后期为30~60 d所对应的斯皮尔曼相关系数都大于0.3,这一结果与上一节的计算结果是一致的。另外,不同监测点所对应的相关系数随着滞后天数的变化呈现出的变化趋势基本一致,即从滞后期为30~60 d的变化过程中,随着滞后期的增加,相各监测点对应的相关性系数都是先增加,滞后期为40 d时,除监测点GZX297之外的监测点所对应的相关性系数都达到了最大,之后随着滞后天数的增加,相关系数又逐渐减小。表4中的相关系数的值基本大于表2中的值,这是由于表2的结果是采用2008—2017年内的每月数据所得出的,数据时间跨度大,不能充分反映出数据之间的相关性,而表4为每日监测数据的计算结果,数据之间具有较好的连续性,能够最大程度地还原滑坡位移量与水位变化之间的关系。

表4 累计位移量与库水位高程之间的斯皮尔曼相关系数Table 4 Spearman’s rank order correlation coefficient between daily cumulative displacement and water level elevation
通过对小时间尺度的数据的定量计算分析,不仅验证了滑坡位移量与水位高程之间的正相关性,还将滞后期的计算值精确至40 d,尽管滞后期的计算值与真实值之间还存在一定的误差(误差分别为17%与20%),但是相比较于滑坡长达数月的变形时间来说,这一误差是能够接受。
4 结论
先对木鱼包滑坡监测数据进行了定性分析,之后借助于相关性检验的方法,计算了不同时间尺度下的监测数据(监测点位移量、水位高程、降雨量)之间的相关性系数,最终取得了如下结论。
(1)定性分析发现木鱼包滑坡产生加速变形往往是发生于库水位高而降雨量少的旱季,而在月降雨量超过200 mm的时间段却少有较大变形过发生,因此初步判定水位高程是影响木鱼包滑坡稳定性的主要原因。
(2)大时间尺度的监测数据的相关性计算结果明滑坡的位移量与滞后期1~2个月内的水位高程之间的相关系数最大,6个监测点的相关系数的平均值为0.43,最大为0.487,这说明滑坡的位移量与水位高程之间的正相关性。滑坡位移量与降雨量几乎全部小于0.2,只有一个大于0.3,这说明坡位移量与降雨量之间并没有明显的相关性。
(3)小时间尺度的数据的计算结果在验证库水位高程是影响木鱼包滑坡稳定性的主要因素的同时,还进一步将滑坡出现加速变形与水位升高之间的滞后期的计算值精确到了40 d。
(4)结合定性分析与定量计算的结果,确定水位高程的增加是木鱼包滑坡出现加速变形的主要驱动因素,这一结论与其他学者对木鱼包滑坡取得的认识是一致的。
