贵州尖山营变形破坏特征及位移预测分析

2021-10-15李海军李阳春

科学技术与工程 2021年27期

丁恒，李海军，李阳春

(1.贵州省地质环境监测院，贵州 550000; 2.成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都 610059)

斜坡位移预测是指根据收集大量的资料与数据，采用一定技术手段对斜坡在时间与空间上的变形破坏进行预报。斜坡位移预报研究始于20世纪60年代，中外许多专家和学者经过近几十年的不断探索和努力，提出了多种预测模拟及预测方法。

李秀珍[1]认为时间预报的核心任务是明确预报模型及预报依据，通过监测数据以及现场调研，建立预报模型；殷坤龙等[2]、邓洪高等[3]讨论了信息模拟与Verhulst模型得基本原理后，并以不同工程实例得到验证；针对在 Verhulst 模型中把第一个数据点作为已知条件的理论依据不存在，可能导致预报精度较低问题，贺小黑[4]基于MATLAB程序，对Verhulst 模型中计算推导公式进行改进，并推导出Verhulst模型和速度最大值判据预报滑坡发生时间的计算公式；李潇等[5]、杨帆等[6]通过最小二乘支持向量模型等来进行预测；刘继奎等[7]对灰色预测模型 GM(1，1)进行研究，并用于宿州市某滑坡沉降位移的监测预报中，结果表明，该模型能很好地预测滑坡位移的变化趋势，又有张贵钢等[8]、郭江等[9]、胡华等[10]对灰色预测模型GM(1，1)在动态、新陈代谢、以速率为参量GM(1，1)模型上分别做出进一步的改进；孙世国等[11]以监测数据为基础，采用时间序列与灰色理论预报的结果相结合，对滑坡的位移变化进行预报，结果显示，两种预报模型的结合分析，提高了预报的准确率及平均预测精度；吴益平等[12]、张楠等[13]通过神经网络理论，对滑坡进行预测；周萃英[14]、刘华明等[15]采用非线性理论建立预报模型，并在工程案例上得以应用，为滑坡预报提供一种新方法。

基于现场地表位移监测数据，采用时间序列分析方法，对尖山营不稳定斜坡的位移变化进行预测。不稳定斜坡位移预测对地质灾害的减防控工作起着重要作用，对降低地质灾害造成的人员伤亡与经济损失具有重要意义。

1 边坡概况

尖山营不稳定斜坡位于贵州高原西部，地形跌宕起伏，切割强烈，属于构造侵蚀而成的低中山至中低山地貌。边坡平面图如图1所。

图1 不稳定斜坡平面图Fig.1 Plan of unstable slope

不稳定斜坡区域内地层出露有第四系(Q)：厚0～80.50 m，主要以残积物、坡积物为主，分布在同向坡及单斜谷中；下统飞仙关组(T1f)：主要分布于斜坡区西部，岩性为上部为灰绿色、紫色相间，钙质泥岩与细砂岩互层，中部及底部夹较多的细砂岩透镜体，中部为粉砂质泥岩或细砂岩；底部见黑色斑粒，碳化植物化石，总厚530.03～875.16 m，平均厚632 m；二叠系上统龙潭组(P3l)：由灰—深灰色粉砂岩、泥岩及煤组成，主要分布于滑坡区东部。

2 变形破坏特征

尖山营从2005年开始进行大规模采煤，一直延续2019年，且开采煤层多达8层。坡体前缘均较缓，坡体后壁近于陡立，原因在于采空区的顶板塌陷和变形导致尖山营坡斜坡中岩层产生向其临空面方向蠕滑变形，这种变形也进一步导致尖山营斜坡上NW-SE向裂缝的逐渐发展，同时也引起不稳定斜坡变形体中岩体变形破裂的进一步发展。

通过2016—2020年影像资料对比(图2)，发现这几年的斜坡的崩塌堆积体面积的越来越大，变形体的后缘边界正在越来越后进行扩展，特别是靠北侧的部位垮塌的面积越来越大，裂缝也越来越多，这个同煤层开采基本是同步的，逐渐演化成尖山营不稳定斜坡。变形区后缘裂缝面粗糙，呈锯齿状，北西侧裂缝呈羽状搌布。泥岩软弱层层面光滑，斜坡岩体被层面和节理面均匀切割，根据现场地质调查，形成类似碎裂化的岩体，如图3所示。

图2 尖山营变形破坏图Fig.2 Deformation and failure diagram of Jianshanying

图3 破碎岩体Fig.3 Broken rock mass

3 监测分析

3.1 监测点布置

不稳定斜坡自动化监测系统共布设了11个地表位移监测点，如图4所示。地表位移监测编号分别为GPS01～GPS11，其中GPS05为表面位移基准站。顺着滑坡山崖顶从下往上布置5个监测点，顺着滑坡山崖底布设3个监测点，在下方煤矿厂区附近村庄布设2个监测点。选取位移变化较大的GPS03、GPS04、GPS09、GPS10四个地表位移监测点进行分析和预测。

图4 监测点布置平面图Fig.4 Layout plan of monitoring points

3.2 地表位移数据分析

监测点于2018年6月份安装结束，后期对现场设备进行定期巡检、调试、诊断、维修等工作。在巡检过程中发现GPS03监测点监测数据出现异常，2019年5月对所有监测点进行调试及维修，于2019年5月20日所有监测点重新开始工作，测点GPS04数据被清零，测点GPS09、GPS010原先累计位移数据保留。取2019年5月20日—2020年9月17日期间的监测数据对尖山营不稳定斜坡现状稳定性进行分析。监测点布置X表示南北方向，向北为正，向南为负；Y表示东西方向，向东为正，向西为负；Z表示重力方向，向上为正，向下为负。各监测点数据分析如图5所示。

图5(a)为GPS03测点的累计位移历时曲线图。从图中数据变化趋势可以看出，2019年5月20日—2019年12月4日期间，该点位在X、Y、Z3个要素中，X方向累计变化811.9 mm,Y方向累计变化量为286.1 mm，Z方向累计变化量-164 mm。在2019年12月5日出现陡增，1 d之内位移变化量较大，X方向位移变化量达到1 236.3 mm，增加了424.4 mm，Y方向位移变化量达到482.2 mm，增加了196.1 mm，Z方向位移变化量达到-239.3 mm，增加了-75.3 mm，合位移达到1 330.05 mm，增加了453.74 mm。主要由于近期在该部位进行煤层开采，受采动的影响，坡体内部产生了大量裂隙，多在采空区临时支护处形成，当临时支护失受到破坏而失去支护能力时，采空区岩体发生较大弯曲变形且下沉，并迅速向上部岩体扩展，导致在该点附近产生较大变形。

图5(b)为GPS04测点的累计位移历时曲线图，测点GPS04位于山顶南部，从图中数据变化趋势可以看出，在2019年5月20日—2020年9月17日期间各个方向的位移变化量都较小。到2020年9月17日为止，X方向位移累计变化量为100.5 mm，Y方向位移累计变化量为51.9 mm，Z方向位移累计变化量为-101.9 mm，合位移为161.2 mm。

图5(c)为GPS09测点的累计位移历时曲线图，测点位于尖山营不稳定斜坡的陡坎之上，且呈缓慢增长的发展趋势，到2020年9月14日为止，GPS09测点在X方向位移累计变化量为110.9 mm，Y方向位移累计变化量为43.2 mm，Z方向位移累计变化量为-157.0 mm，合位移为204.8 mm；X、Y曲线变化趋势缓慢，该方向上主要发生水平位移，尖山营滑坡主要是受到采动影响，加之一侧为临空面，所以在水平方向上变化量一直在缓慢增长；Z曲线变化趋势呈缓慢斜线上升，由于采空区中的临时支撑失去了支护能力，而逐渐破坏，导致顶板岩体弯曲下沉。

图5(d)为GPS010测点的累计位移历时曲线图。测点都位于尖山营不稳定斜坡的陡坎之上，且呈缓慢增长的发展趋势，GPS10测点在X方向位移累计变化量为267.2 mm，Y方向位移累计变化量为35.8 mm，Z方向位移累计变化量为156.8 mm，合位移为316.8 mm。X、Y曲线变化趋势缓慢，该方向上主要发生水平位移，尖山营滑坡主要是受到采动影响，加之一侧为临空面，所以在水平方向上变化量一直在缓慢增长；Z曲线变化趋势呈缓慢斜线上升，由于采空区中的临时支撑失去了支护能力，而逐渐破坏，导致顶板岩体弯曲下沉。

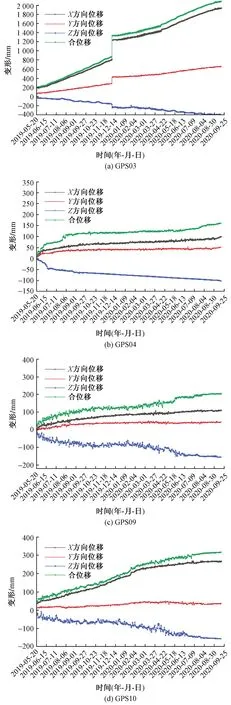
图5 GPS地表位移监测分析Fig.5 GPS surface displacement monitoring analysis

4 基于时间序列预测分析

斜坡位移是随时间的变化的一个时间序列，时间序列中的数据的大小反映了数据内部的相互联系和变化规律。

尖山营不稳定斜坡位移变化主要是由于自身地质条件的演化以及外部因素综合作用的结果。时间序列中包含趋势项、季节项、周期项、随机项的影响，在斜坡变形演化过程中，其根本性因素，自身地质条件的演化构成趋势项位移；季节变化所带来的温度变化、降雨量变化进而影响斜坡位移，可以归纳进周期项位移；人类工程活动对斜坡位移的影响可以归入随机项位移。在本文中，由于采煤活动影响过于广泛，破坏了矿山自身地质条件的演化规律，因而将其归入趋势项中，则尖山营不稳定斜坡位移时间序列模型为

Y=X(t)+Z(t)

(1)

式(1)中：Y为位移时间序列；X(t)为趋势项位移函数；Z(t)为周期项位移函数。

对于趋势项位移函数，一般采用线性函数以及幂函数、指数函数进行拟合，其单调性与斜坡趋势向位移函数吻合度较高；斜坡位移时间序列一般在趋势项拟合函数上下波动，其中会含有一个或多个周期、振幅不同的三角函数，即采用三角函数进行拟合。

4.1 斜坡位移函数拟合

在趋势项X(t)函数中，需要根据斜坡位移增加趋势选择合理的拟合函数。坡体变形处于等速蠕变阶段，坡体表面位移呈现线性增加的趋势，因而选用线性函数对坡体表面位移趋势项X(t)进行拟合，所以建立趋势项X(t)函数为

X(t)=at+b

(2)

式(2)中：a为系数；b为常数。

在周期项Z(t)函数中，随着每年雨季的到来，边坡变形呈现较快增长的趋势，进入旱季边坡变形则趋缓，每年如此，而且温度的年际变化也使坡体表面发生周期性的变化，所以在周期函数Z(t)中，用正弦函数进行拟合。建立周期函数Z(t)为

Z(t)=csin(dt+e)+f

(3)

式(3)中：c为振幅；d为周期常数；e为相位；f为常数。

综合式(1)～式(3)可得到整个数学模型，即

Y=at+b+csin(dt+e)+f

(4)

经过合并整理，将常数项合并为A后得

Y=at+csin(dt+e)+A

(5)

4.2 趋势项及周期项分析

根据每个监测点的合位移曲线，采用MATLAB数学软件编程计算。

4.2.1 趋势项函数拟合

根据每个监测点的合位移曲线形状，GPS03在2019年12月5号之前出现位移突变，合位移出现陡增情况，本身地质条件演化情况在受到采煤活动影响后，进入了一个新的不平衡状态，所以在构建数学模型时，在趋势项拟合时选取2019年12月5日—2020年9月17日的监测数据进行拟合，其他监测点均由2019年5月21日开始预测。采用一元一次函数作为趋势项函数在MATLAB中进行拟合，监测点GPS03、GPS04、GPS09、GPS10趋势项拟合公式依次为

X(t)=2.61t+1 286

(6)

X(t)=12.97t0.410 8

(7)

X(t)=0.284 9t+59.56arctant-29.2

(8)

X(t)=0.525 2t+49.04arctan(t+0.413 6)

(9)

根据式(6)～式(9)绘制各监测点的趋势项拟合图像与实测数据对比图，如图6所示。

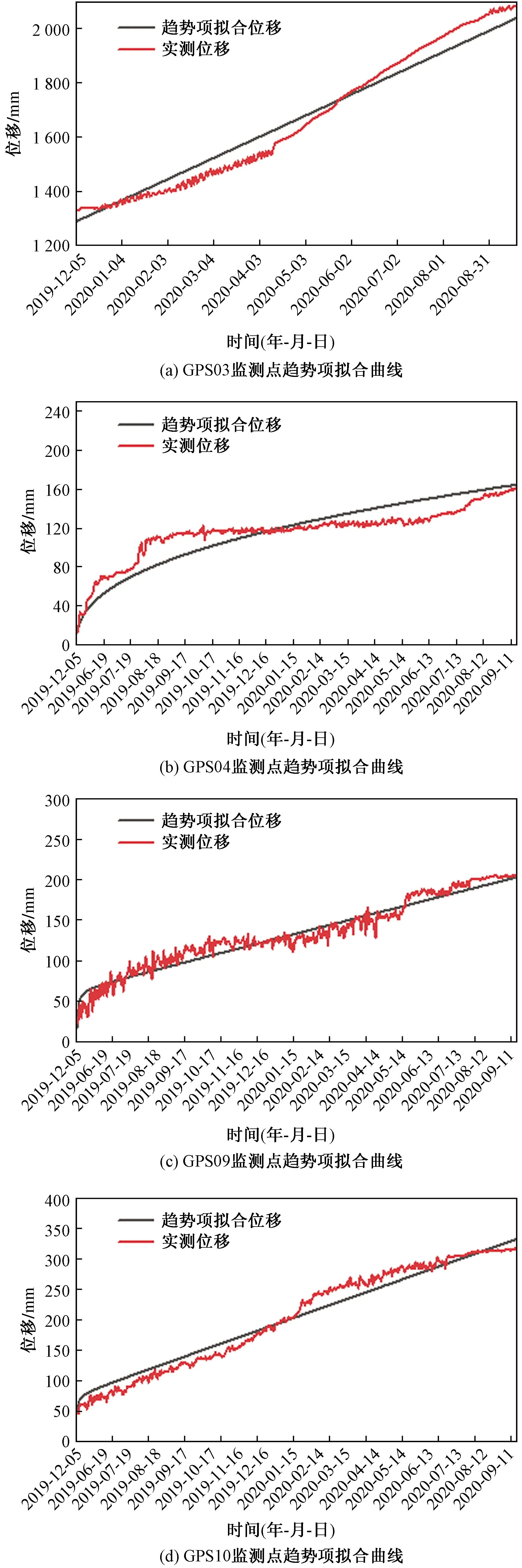
图6 各监测点趋势项位移拟合图Fig.6 Trend item displacement fitting diagram of each monitoring point

与实际曲线对比可见，实测数据在趋势项拟合函数上下波动，存在周期项误差，主要是由于监测仪器在工作过程中受到卫星信号强弱影响，以及受到煤层采动影响。其中，监测点GPS04的趋势项X(t)函数平均相对误差最大为15.81%，监测点GPS10的趋势项X(t)函数平均相对误差最大为1.84%，其他监测点趋势项的误差都小于等于9.88%。可以看出，趋势项拟合函数的相对误差较大，因此，需进行周期项修正。

4.2.2 周期项合位移拟合

使用实测位移值减去趋势项X(t)位移值即可得到周期项位移，从图7可见，周期项位移整体上呈现正弦函数或呈现余弦函数波动，从局部来看，周期项函数位移曲线存在多个波峰波谷，周期在1～6个月之间。因此，采用正弦函数与余弦函数叠加对周期位移进行修正，通过MATLAB拟合得到Z(t)：监测点GPS03、GPS04、GPS09、GPS10周期项拟合公式依次为

Z(t)=-64.22sin(0.020 87t-0.600 2)

(10)

Z(t)=-19.19sin(0.011 82t-96.97)

(11)

Z(t)=10.91sin(0.02t-1.002)

(12)

Z(t)=-19.8sin(0.013 6t+0.322 9)

(13)

根据式(10)～式(13)绘制各监测点的周期项拟合图像与周期项对比图，如图7所示。

图7 各监测点周期项位移拟合图Fig.7 Fitting diagram of the periodic term displacement of each monitoring point

从Z(t)周期项修正函数图像与周期项位移图像中可以看到，通过正弦函数与余弦函数的叠加，周期项拟合函数Z(t)与实际曲线吻合度较高，能够拟合降雨、季节、温度变化等带来的周期性位移波动。

4.3 合位移预测分析

将趋势项位移拟合函数X(t)与周期项位移拟合函数Z(t)叠加，即可得到合位移拟合函数Y。监测点GPS03、GPS04、GPS09、GPS10趋势项拟合公式为

Y=2.61t+1 286-64.22sin(0.020 87t-

0.600 2)，R2=0.999

(14)

Y=12.97t0.410 8-19.19sin(0.011 82t-

96.97)，R2=0.970 2

(15)

Y=0.284 9t+10.91sin(0.02t-1.002)+

59.56arctant-29.2，R2=0.957 2

(16)

Y=0.525 2t-19.8sin(0.013 6t+0.322 9)+

49.04arctan(t+0.413 6)，R2=0.995 2

(17)

根据式(14)～式(17)绘制各监测点的合位移拟合图像与实测合位移数据对比图，如图8所示。

图8 各监测点合位移拟合图Fig.8 Fitted displacement diagram of each monitoring point

从图8可见，合位移拟合曲线与实测值吻合度较高。根据式(14)～式(17)，合位移拟合优度R2都接近于1，拟合优度R2最大为监测点GPS03达到0.999，拟合优度为优，拟合优度R2最小的监测点为GPS09达到0.957 2，拟合优度较好，其余监测点拟合优度R2为0.957 2～0.999，在总体上来说，模型的拟合优度好，得到的拟合函数数学模型的准确度较高，可以用于尖山营不稳定斜坡的滑坡位移预测。