考虑非线性接触及车辆动载铺装层动力分析

2021-10-15郝艳广袁龙文韩劲龙陈金鑫

科学技术与工程 2021年27期

郝艳广，袁龙文，韩劲龙，陈金鑫，陈璐

(1.中交二航局建筑科技有限公司, 武汉 430000; 2.海工结构新材料及维护加固技术湖北省重点实验室, 武汉 430040; 3.长沙理工大学土木工程学院, 长沙 410000)

由于公路交通发展迅速，钢-混组合桥已成为中国公路交通运输重要组成部分。随着钢-混组合桥服役时间延长，铺装层与钢材之间的滑移、开裂日益突出。针对这一现象，有必要进行深入研究，探究铺装层与钢材的滑移、开裂机理。

针对铺装层与钢材之间的滑移、开裂，中外学者已进行大量研究：Stoura等[1]针对大型车-桥系统，提出利用二阶常微分方程求解车-桥相互作用问题的动态划分方法，该方法可减少计算量；Shen等[2]基于模型缩聚理论提出求解车桥耦合问题新理论，并利用MATLAB进行计算分析，验证了该理论可提高求解精度并减少求解时间；Liu等[3]将移动荷载施加于铺装层，计算铺装层拉应力，研究重载及温度对铺装层沥青混合料力学行为的影响；周瑞娇等[4]利用ANSYS建立车-桥耦合模型，分析车辆速度和路面不平度等因素对桥梁动力响应以及跳车的影响；陈水生等[5]提出采用相位角相干生成车轮相干桥面不平顺方法并验证，结果表明，车轮相干桥面不平顺增大桥梁、车辆竖向振动响应，因此有必要考虑各车轮相干性关系。

基于上分析可得，相关研究对车辆动载作用下铺装层动力响应研究较少，未能考虑轮胎-铺装层非线性接触，因而存在一些不足之处。利用一定理论建立车辆、橡胶轮胎以及铺装层-简支桥有限元模型，考虑轮胎-铺装层非线性接触以及车辆动载，采用显式算法求解，通过相关试验验证，研究铺装层动力响应，并分析路面不平度激励对铺装层动力响应的影响。

1 构建车辆模型

1.1 车辆多体动力学建模

根据车辆振动特点，将其适当简化。R为惯性参考点，与悬架、车轴固结，如图1所示。假设车体为刚体B1，利用球较O1约束车体B1与悬架相对自由度，车体可沿OY轴振动；利用旋转铰O2约束轮胎与车轴相对自由度，轮胎受动力矩和路面摩擦力作用，将绕OX轴旋转，使得车辆前进[6-7]。

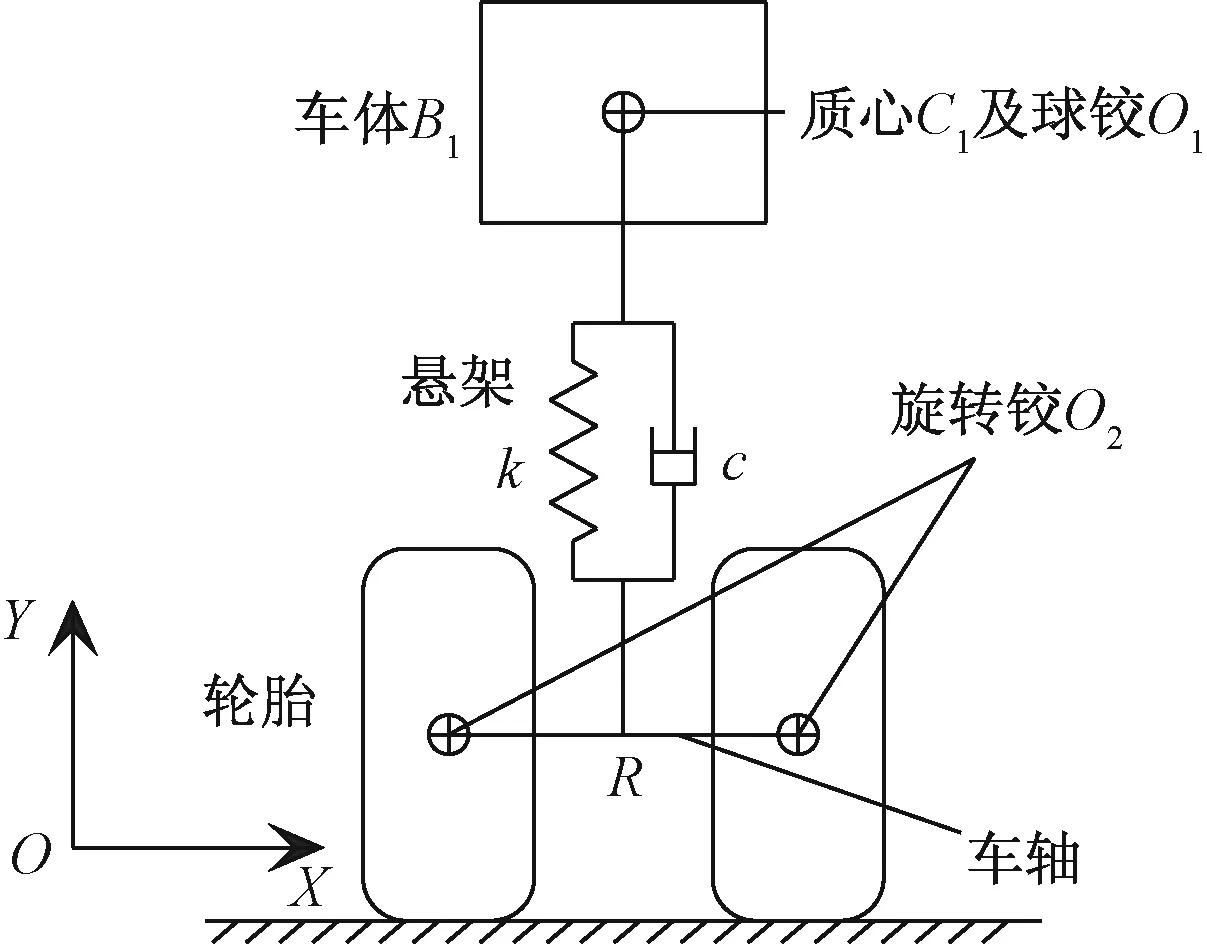
图1 车辆示意图Fig.1 Vehicle diagram

悬架采用线性弹簧阻尼器力元模拟，k表示悬架刚度，c表示悬架阻尼，其作用点为车体质心C1，车体B1受悬架作用。C1初始坐标为q0=(x0,y0,z0)，振动坐标为q=(x,y,z)。悬架对车体B1作用线性弹力F1为

F1=-k(|q|-|q0|)-cq′

(1)

1.1.1 车辆广义坐标

绝对坐标由刚体质心笛卡尔坐标和绕质心转动欧拉角构成。选择笛卡尔坐标系作为R绝对惯性基(O0,e0)，以车体质心C1为基点建立连体基(C1,e1)。车体B1矢径坐标r1由质心C1相对绝对惯性基(O0,e0)的3个笛卡尔坐标(x1,y1,z1)T表示，车体B1姿态坐标采用相对绝对惯性基(O0,e0)的欧拉角λ1i表示，e0表示基底，其中下标i为欧拉参数编号，i=0,1,2,3。欧拉角坐标阵Λ1为

Λ1=(λ10,λ11,λ12,λ13)T

(2)

车体B1广义坐标q1为

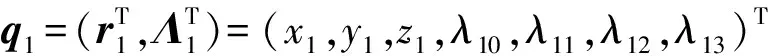
(3)

1.1.2 无约束车体动力学方程

解除车体B1所有动力学约束，则车体B1无约束动力学方程[7]为

M1q″1=Q1

(4)

(5)

(6)

式中：m1为车体B1质量；E为单位阵；L1为欧拉角坐标阵Λ1引入矩阵；J1为车体B1相对其连体基惯性张量的矩阵；F1和T1为作用于车体B1上全部外力主矢坐标矩阵，车体无约束动力学方程为

Mq″=Q

(7)

1.1.3 车体动力学约束方程

球较O1及旋转铰O2构成一组完整约束，其约束方程、速度方程和加速度方程为

Φ1(q,t)=0

(8)

Φ1qq′=-Φ1t

(9)

Φ1qq″=ζ1

(10)

ζ1=-[(Φ1qq′)qq′+2Φ1qtq′+Φ1tt]

(11)

1.1.4 受约束车体动力学方程

对于受约束车体，引入与方程对应的拉格朗日乘子μ。利用高斯加速度变分，可得车体力学微分-代数方程为

(12)

1.2 车辆有限元模型

根据上述分析，基于ABAQUS建立1/4车辆有限元模型。利用连接单元建立悬架与车轴，分别赋予Cartesian属性和Hinge属性[8]。车辆有限元模型如图2所示，车辆参数如表1所示。

表1 车辆参数

图2 车辆有限元模型Fig.2 Finite element model of vehicle

2 构建轮胎模型

相关研究以质量-弹簧体系模拟橡胶轮胎，与实际存在较大误差[9-11]。基于ABAQUS建立全钢丝子午线重载轮胎(轮胎型号11.00R20)，最大气压850 kPa，充气后外缘直径1 050 mm，充气后外缘断面宽282 mm。

2.1 Mooney-Rivlin模型

采用统一数学模型建立橡胶本构关系。假定橡胶不可压缩并考虑高体积模量，利用应变能密度表征橡胶物理特性[12-14]。由唯相理论可知，Cauchy-Green变形张量不变量I1、I2、I3可表示应变能密度函数，即

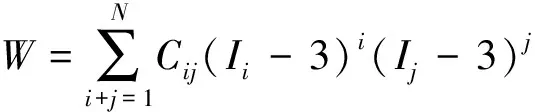
(13)

式(13)中：Cij为材料常数，由试验获得。

应变能密度函数是主伸长率偶次幂函数，主伸长率与变形张量不变量满足关系

(14)

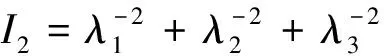
(15)

(16)

当橡胶不可压缩时，I3=1。

应变能密度函数可进一步表示为

W=W(I1,I2,I3,C1,C2,…，Cm,d1,d2,…，dn)

(17)

式(17)中：Ik(k=1,2,3)为应变不变量；Ci(i=1,2,…,m)与dj(j=1,2,…,n)分别为超弹性材料力学特性常数、压缩特性常数。N=1时，式(13)修改为

(18)

式(18)即为Mooney-Rivlin模型，Jel为橡胶材料变形体积比，此时应变能密度函数为变形张量不变量的一次项函数。Mooney-Rivlin模型降低了单轴拉伸试验误差，在小应变范围拟合效果良好。该模型表达式简单，参数获取方便，工程中广泛采用[15-16]。

2.2 轮胎有限元模型

轮胎主要包括胎面、胎体、带束层和钢丝帘线等。为提高计算效率并保持一定精度，对其进行适当简化：①胎侧与其邻近材料相同的部分合并；②忽略轮胎花纹，减少计算量。轮胎模型及网格划分如图3所示。

图3 轮胎模型及网格划分Fig.3 Tire model and meshing

橡胶单元为C3D6H和C3D8H，钢丝帘线单元为SFM3D4R，帘线-橡胶复合材料采用Rebar模型[15-16]。橡胶材料参数及钢丝帘线材料参数分别如表2、表3所示。表中C10、C01为超弹性材料剪切参数，D1为超弹性材料可压缩性参数，E为弹性模量，ρ为材料密度，μ为泊松比。

表2 橡胶参数Table 2 Parameters of rubber

表3 钢丝帘线参数Table 3 Properties of steel cord

3 构建铺装层-简支桥模型

3.1 蠕变模型

沥青混合料力学性能复杂，与组成材料密切相关。由文献[15]可知，蠕变试验可用于测定热伴沥青混合料的变形性能，因此采用蠕变模型描述沥青混合料本构关系。车辆动载作用下，沥青混合料总应变为

ε(t)=εe+εp+εc

(19)

式(19)中：εe为弹性应变；εp为塑性应变；εc为蠕应变。假定车辆动载作用下沥青混合料未屈服，则εp=0，式(19)整理为

ε(t)=εe+εc

(20)

温度恒定(本文中沥青混合料模拟温度为20 ℃)，εc为时间t与应力σ的函数，即

(21)

式(21)中：A为幂乘指数，m为等效偏应力阶，n为时间硬化模型的总时间阶数，均为沥青混合料蠕变参数，并与温度相关[15]。

恒载作用下蠕变应变率为

(22)

由式(22)可知，此应变率与时间t有关；非恒载作用下蠕变应变率[15]为

(23)

由式(23)可知，此应变率与时间t无关。车辆动载具有随机性，故采用与时间t无关的蠕变应变率描述沥青混合料力学行为。蠕变参数如表4所示[15]。

表4 蠕变参数Table 4 Creep parameters

3.2 铺装层-简支桥有限元模型

以某高速公路钢-混组合桥为背景，建立铺装层-简支桥有限元模型。铺装层尺寸30 m×10 m×0.3 m，如图4所示；铺装层结构如图5所示；材料参数如表5所示。

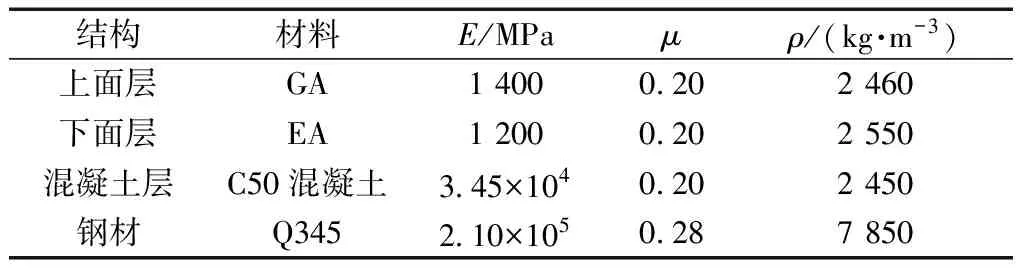
表5 材料参数Table 5 Parameters of materials

图4 铺装层-简支桥模型Fig.4 Model of pavement layer-simply supported bridge

图5 铺装层结构Fig.5 Pavement structure

铺装层与钢材单元均采用C3D8R。铺装层沿厚度方向网格划分如下：上面层为1个网格，网格尺寸为0.025 m；下面层为1个网格，网格尺寸为0.035 m；混凝土层为4个网格，网格尺寸为0.06 m。局部放大的铺装层网格划分图6所示。

图6 铺装层-简支桥网格Fig.6 Mesh of pavement layer-simply supported bridge

4 构建车辆-铺装层-简支桥耦合模型

4.1 路面不平度

路面不平度是Gauss平稳随机过程，一般采用功率谱密度函数表示。利用Fourier逆变换生成路面不平度功率谱密度函数[16]，即

Gd(n)=Gd(n0)(n/n0)-w

(24)

式(24)中：Gd()为位移功率谱密度，m3；n为空间频率，m-1；n0为参考空间频率，0.1 m-1；w为拟合指数。GB/T 7031—2005/ISO 8608:1995《机械振动道路路面谱测量数据报告》将路面不平度分为5个级别[17](A～E)。结合工程实际，选取C级路面不平度。

采用余弦叠加法构建路面不平度，即

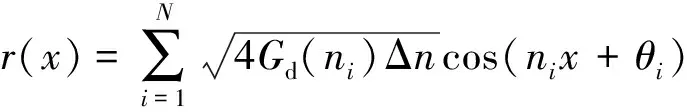
(25)

式(25)中：r(x)为路面不平度；x为纵向距离；Gd(ni)为功率谱密度；ni为空间频率；Δn为频率改变量；θi为[0～2π]内均布的随机相位角。C级路面不平度如图7所示。

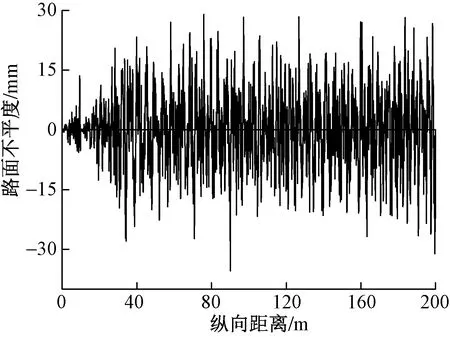
图7 C级路面不平度Fig.7 Pavement roughness of class C

4.2 接触理论

轮胎与铺装层接触状态复杂，存在较多影响因素。基于Kalkeer三维滚动接触理论，建立轮胎-铺装层接触关系，其中铺装层为主面，胎面为从面，接触区域网格划分如图8所示。

图8 接触区域网格划分Fig.8 Contact area meshing

计算主面与从面接触单元位移差，以余能最小为控制变量，分别利用法向接触关系和切向接触关系求解接触区域法向力、切向力以及黏着-滑动状态分布[17-18]，即

(26)

式(26)中：minC1为余能最小值；Ac为可能轮胎-铺装层接触区域；h、μn、pn分别为接触面法向间隙、法向位移、法向接触力；wt、μt、μ′t、pt分别为接触面切向刚性滑移数值、切向位移、前一时刻切向位移、切向接触力；S为积分面积；g为滑动摩擦系数(与接触面材料有关)；P为接触面法向集中力[18]。

假定轮胎-铺装层为平面接触，由以上分析可得，计算时可将任一单元位移与接触面上作用力表示为

μn=pnAnn,μt=ptAtt

(27)

式(27)中:Ann为在法向单位力产生的法向位移；Att为在切向单位力产生的切向位移。

4.3 耦合振动方程

完成1/4车辆模型与铺装层-简支桥模型的构建，列出二者动力学方程并联立求解。耦合振动方程[19-20]为

(28)

式(28)中：y、z分别为车辆、桥梁节点位移向量；Fvg为车辆自重等效节点荷载向量；M、C、K为车辆、桥梁节点质量矩阵、阻尼矩阵、刚度矩阵；Fbv、Fvb为轮胎-铺装层接触区域相互作用节点荷载向量，由形函数分配得到。

将车辆模型和铺装层-简支桥模型视为整体，采用直接积分法求解式(28)。直接积分法有显式和隐式两种求解方法，本文中采用显式求解法[21-22]。

5 实例分析

5.1 验证轮胎模型

利用径向加载试验验证橡胶轮胎有限元模型的可行性。径向加载试验如图9所示，加载-位移曲线如图10所示。径向加载试验释放轮辋垂向位移，约束其他方向位移；加载速度为0.2 kN/s；气压为0.7 MPa。由图10可知，试验值与仿真值曲线趋势接近，最大误差为4.768%，表明所建橡胶轮胎有限元模型具有一定的可行性[13]。

图9 径向加载试验Fig.9 Radial loading test

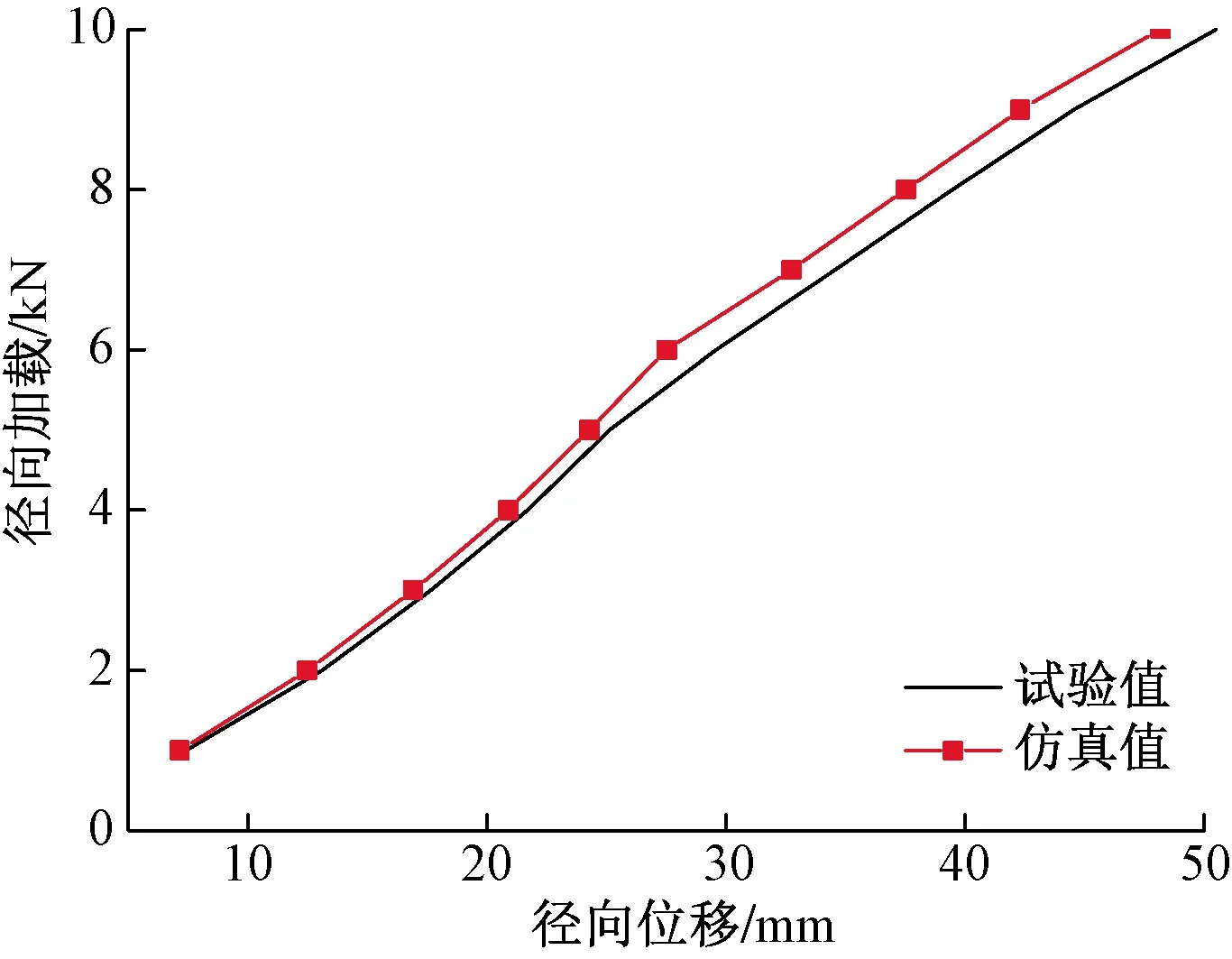
图10 加载-位移曲线Fig.10 Load-displacement curve

5.2 验证铺装层-简支桥模型

以某高速公路钢混组合桥为背景，验证铺装层-简支桥模型。桥梁为简支桥梁，跨度为30 m。铺装层分层铺筑，由上往下依次为聚合物改性沥青混凝土GA、环氧沥青混凝土EA、C50混凝土。利用布设于下面层底部的传感器测量车辆动载作用下下面层底部纵向应变以及桥梁模态，现场测量如图11所示，测量用车如图12所示，应变计规格见表6。

表6 应变计规格Table 6 Strain gauge specification

图11 现场试验Fig.11 Field measurement

图12 试验用车Fig.12 Test the car

测量步骤：

(1)本次测量共设置4组测量断面，每组测量断面间距2 000 mm，其中横向应变计2组，纵向应变计2组，见图13。

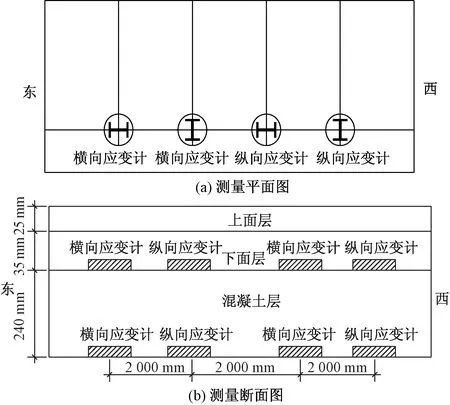
图13 传感器位置Fig.13 Location of sensor

(2)混凝土层：首先将光纤光栅埋入式应变计放置在预先确定的位置，然后浇筑混凝土。

(3)环氧沥青混凝土层：待混凝土层施工完成后，再将沥青混凝土埋入式光纤光栅应变计放置在预先确定的位置，然后铺设环氧沥青混凝土，最后铺设聚合物改性沥青混凝土。

(4)将应变计传感头引出线分别连接电源(本次测量采用柴油发电机)和6224动态采集系统相连，信号仪采用INV360智能处理分析仪。开始测量时，试验车辆预先行驶1～2个回合，待采集器示数稳定后，即可开始正式测量。

(5)本次测量共进行10、15、20、25、30 m/s等6种车辆行驶速度下铺装层动力响应的工况。

将下面层跨中底部纵向应变仿真值与测量值进行对比，如图14所示，误差分析如表7所示，简支桥自振频率仿真值与测量值的对比如表8所示。由图14、表7和表8可知，仿真值与测量值曲线比较吻合，误差在容许范围内，表明所建铺装层-简支桥模型的计算假定和计算结果符合实际情况。

图14 下面层底部纵向应变Fig.14 Longitudinal strain at the bottom of the lower layer

表7 误差分析Table 7 The error analysis

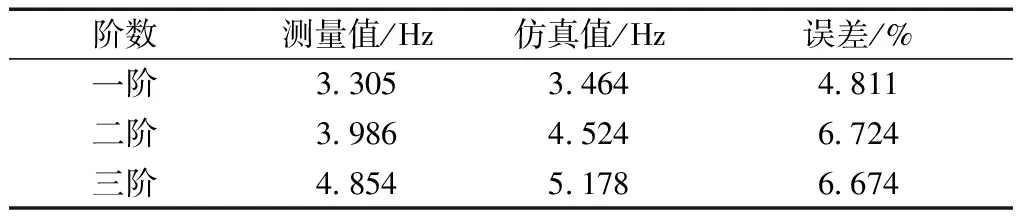
表8 自振频率对比Table 8 Natural frequency contrast

5.3 铺装层动力响应分析

5.3.1 无路面不平度

为研究铺装层动力响应，选取Vz=30 m/s时，铺装层应力响应时程曲线。观察点为铺装层跨中，如图15所示，各项应力响应如图16所示。

图15 观察点Fig.15 Observation point

由图16(a)可知，上面层与下面层纵向应力以受压为主，上面层最大压应力为0.245 MPa，下面层为0.240 MPa，混凝土层纵向应力以受拉为主，最大拉应力为1.290 MPa。表明混凝土层与钢材接触面拉应力明显。

由图16(b)可知，沥青面层与混凝土层横向应力差别较大。上面层与下面层纵向应力均以受压为主，上面层最大横向压应力为0.277 MPa，下面层为0.267 MPa。混凝土层横向应力以受拉为主，最大横向拉应力为0.805 MPa。当车辆接近观察点时，混凝土层横向应力出现拉压交变；车辆远离观察点时，无明显拉压交变。

由图16(c)可知，铺装层纵向剪应力以拉压交变为主，各层均表现出相同的变化趋势。上面层最大拉应力为0.026 MPa，最大压应力为0.053 MPa；下面层最大拉应力为0.058 MPa，最大压应力为0.083 MPa；混凝土层最大拉应力0.027 MPa，最大压应力为0.038 MPa。由上至下，纵向剪应力呈现出先增大后减小的趋势，下面层出现最大拉应力和最大压应力。拉应力易导致铺装层出现纵向裂缝，在重复交通荷载作用下，铺装层纵向剪应力拉压交变明显，极易出现疲劳裂缝。

由图16(d)可知，沥青层与混凝土层横向剪应力均表现出拉压交变，但差别较明显。上面层最大拉应力为0.008 MPa，最大压应力为0.006 MPa；下面层最大拉应力为0.015 MPa，最大压应力为0.010 MPa；混凝土层最大拉应力0.061 MPa，最大压应力为0.109 MPa。由上至下，横向剪应力逐渐增大，且混凝土层横向剪应力明显大于沥青面层。当车辆接近观察点时，混凝土层先压后拉，沥青层先拉后压。

由以上分析可知，混凝土层横向应力、纵向应力、横向剪应力受拉明显，下面层纵向剪应力拉压交变明显。

5.3.2 C级路面不平度

为研究路面不平度对铺装层动力响应的影响，基于上述分析，选取C级路面不平度下下面层和混凝土层动力响应时程曲线，各项应力时程曲线如图17所示。

由图17(a)可知，混凝土层无路面不平度最大纵向拉应力为1.290 MPa，C级路面不平度最大纵向拉应力为2.230 MPa，比无路面不平度增大72.868%，应力时程曲线出现较多尖角，表明振动明显。

由图17(b)可知，混凝土层无路面不平度最大横向拉应力为0.805 MPa，C级路面不平度最大横向拉应力为2.060 MPa，比无路面不平度增大155.9%涨幅明显，且C级路面不平度激励下，横向应力时程曲线亦存在较多尖角，表现出随机振动现象。

由图17(c)可知，混凝土层横向剪应力出现拉压交变，无路面不平度最大拉应力0.061 MPa，最大压应力为0.109 MPa。C级路面不平度最大拉应力为0.067 MPa，最大压应力为0.231 MPa，分别比无路面不平度增大9.836%，111.927%，压应力涨幅明显，且应力时程曲线存在明显尖角，随机振动加剧。