基于WGN算法的城市路网拥堵路段诊断分析

梁晓辉, 陈松利, 李丹岚

(内蒙古农业大学能源与交通工程学院， 呼和浩特 010018)

随着机动车保有量的增加，交通需求持续增长，交通拥堵开始成为城市交通的普遍问题，严重影响了居民的工作效率与生活质量。根据产生原因的不同，交通拥堵可分为常发性和偶发性两类。与偶发性拥堵的随机性不同，常发性拥堵由交通需求超出道路设施正常容量所致，一般发生在高峰时间，具有可预测性。所以，常发性拥堵的识别成为我国交通管理工作的重中之重[1]。

以往研究中对于常发性拥堵的评价多是对拥堵时间和空间进行简要融合或单维分析。张婧[2]将不确定性处理技术和轨迹信息挖掘在线分析技术融入交通拥堵时空分布特征的分析研究，构建了在线缓堵控制框架。杨海强等[3]提出基于车辆全球定位系统(gobal positioning system,GPS)轨迹数据的网格级别的拥堵判别方法，并利用基于密度的空间聚类算法识别城市常发性拥堵区域。江航[4]通过构建宏观基本图信号控制评估方法主动引导交通演化，均衡路网交通负荷，实现预防路网交通拥堵的目标。韩值[5]从交通流在时间与空间上的等效性基础上，建立了道路交通流时空关系模型。王妍颖等[6]通过大数据技术对道路的拥堵评价指标进行计算和分析，得到了道路网交通拥堵的潜在规律。贾若等[7]从传统交通流理论与机器学习两方面综述了交通拥堵判别的方法。胡启洲等[8]根据交通拥堵在时间和空间上的分布特性，建立基于价值函数的城市路网交通拥堵的测定指标体系。曹堉[9]提出了一种基于贝叶斯网络的城市道路交通拥堵多原因自动实时识别方法。熊励等[10]针对城市道路交通拥堵及持续时间辨识问题，构建了基于Mapreduce的多元对数线性回归交通拥堵预测模型和基于生存分析的交通拥堵持续时间模型。周辉宇[11]从时间和大数据规则挖掘角度对拥堵建模，使用时间序列规则挖掘算法建立交通拥堵传导规律模型，并基于传导规则预测未来交通流状况。王芹等[12]通过提取实时路况数据，借助Arcgis软件，运用广义G统计量、热点分析方法对交通拥堵进行研究。诸云等[13]在分析城市道路网络交通拥堵博弈关系的基础上，建立了以交通拥堵程度为下层决策目标、经济费用为上层决策目标的城市路网优化双层规划模型。

综上所述，中外在交通拥堵评价和交通拥堵识别领域均已开展了许多研究和实际应用工作，有较强的指导性，但着眼于结构性拥堵的研究较少。交通需求在空间上的分布是不均匀的，这与一个城市的交通网络拓扑结构形式、城市用地性质、区域就业岗位、区域经济发展状况等诸多因素有关。交通需求的空间不均匀性是导致交通拥挤路段和交通高负荷地区的重要因素。道路网络是一个复杂的网络系统，道路结构不尽合理是导致拥堵形成的一个重要原因。既有研究中，往往按照行政区域对道路网络进行区域划分，并没有考虑到路网结构本身的性质，因此不能发现路网结构中存在的一些问题，对进一步的研究和分析造成了一定的不良影响。因此，现从中观路网结构角度出发，以道路网络的结构性质为依据，对城市道路网络进行组团划分，然后找出路网结构中的关键路段，再以小区间OD(origin-destination)量，即起讫点交通量作为权重，进一步找出路网中的拥堵路段，为后续的研究分析做铺垫。并尝试进一步运用到案例城市道路网络中，以验证方法的准确性。

1 WGN算法理论依据

1.1 算法思想

WGN(weighted Girvan-Newman)算法，即加权组团划分算法，是由复杂网络理论中的非重叠社区识别算法-GN(Girvan-Newman)算法改进得到。如图1所示，网络由不同的组团组成，这些组团的特征是：组团内部的节点紧密相连，而组团之间的节点联系较少。那么位于不同组团的节点之间的最短路径必将经过那些少量的组团之间的边。这样，连接不同组团的边将比组团内的边具有更高的介数值，记为Bij。

其中边介数的定义为：以网络中每一个节点i为源节点，计算它到其他节点j的最短路径，并以这些最短路径经过的每条边的次数作为该边的介数[14]。边的介数越大，说明在交通流移动中通过该边的交通量也会越大，也越容易发生交通堵塞，该边在网络中也会越重要。通过逐步移去这些边介数较高的边就能够把它们连接的组团分割开来。组团结构网络如图1所示。

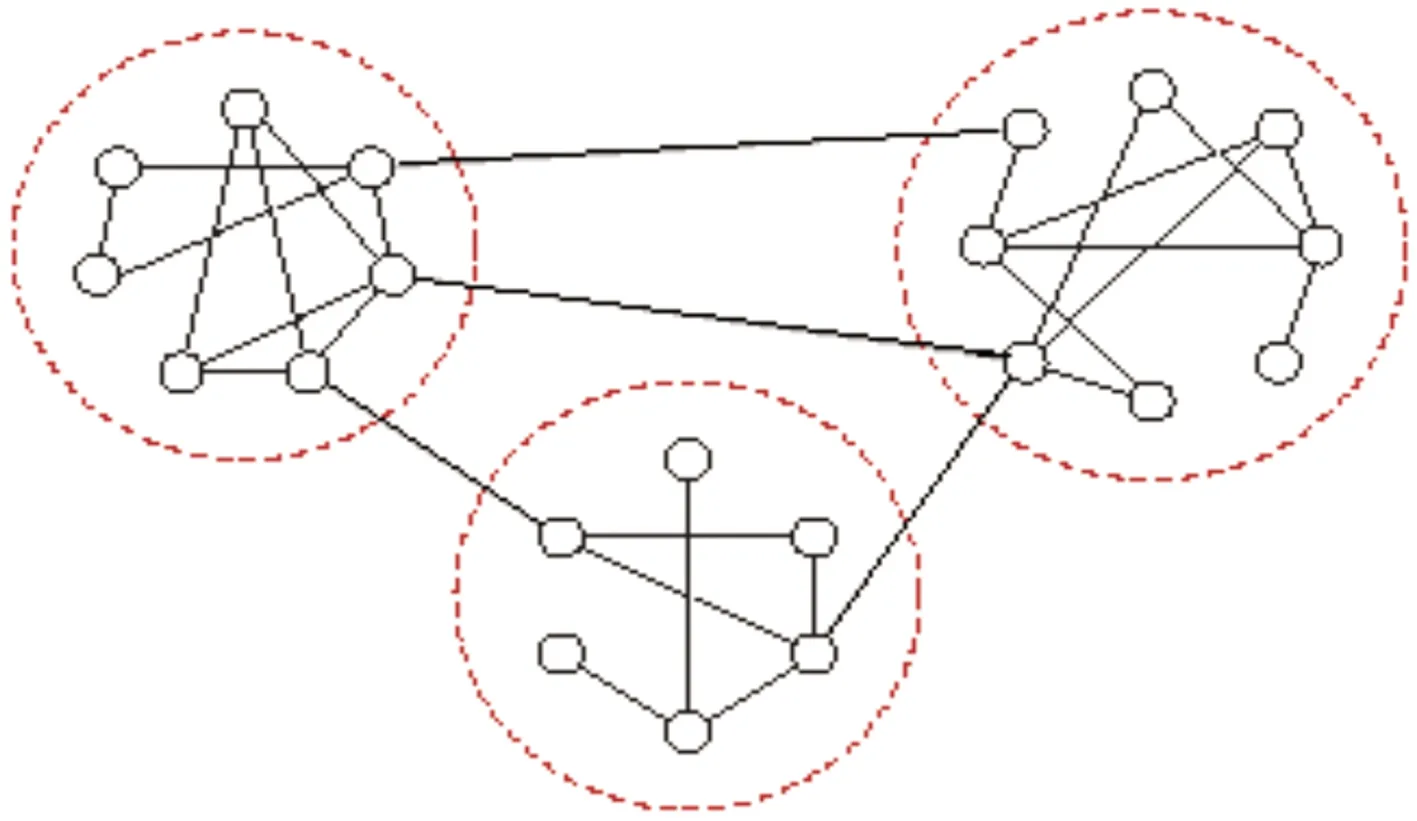
图1 小型组团结构网络示意图Fig.1 Network of small group structures

1.2 算法假设

城市道路交通系统本身是由道路系统、流量系统和管理系统组成的一个复杂巨系统。城市道路网络由交叉口和连接它们的路段组成，交通流在网络上流动。本文中把交叉口和路段分别抽象为网络中的节点和边，车辆在边上行驶遇到的阻抗(如行驶时间等) 对应于边上的权重，考虑路段的方向性，把城市交通网络抽象为一个复杂的双向加权网络。由于城市道路网络具有其独特的性质，将WGN算法应用到城市道路网络的组团划分时，本文中做了以下假设。

(1)所有用户都试图选择最短路径到达其目的地。

(2)所有用户都根据同一评判标准判断路径长短。

(3)所有用户都可以得到当前交通状态下可供路径选择的全部信息[15]。

目前GPS导航系统、高德地图等智能化诱导系统在城市交通中的广泛应用，保证了上述假设的有效性。

1.3 算法关键参数

把交叉口和路段分别抽象为网络中的节点和边，即以C=(N,A)表示城市道路网络，其中N表示为城市道路交叉口的集合，A表示为城市道路路段的集合。把道路交叉口等效为网络中的节点i，路段等效为网络中的边，采用 (eij,eji,tij,wij)表示。其中eij为路段ij的正向弧，eji为路段ij的反向弧，tij为通过该路段的自由流时间，wij为该路段的单位流量权重系数，它表征了在单位时间内能通过路段ij断面的单位流量。假设路段ij中eij和eji的使用情况完全相同，则其tij和wij都相等。

2 道路网络组团划分步骤

假设将城市交通网络划分为k个组团。定义一个k×k维的对称矩阵E=(eij)k×k，其中元素eij表示网络中连接两个不同组团间节点的路段在所有路段中占的比例；这两个节点分别位于第i个组团和第j个组团。在这里所说的所有的路段是在原始网络中的，而不必考虑是否被WGN算法移除。另外每个路段的单位流量权重系数为wij。

定义每行(或者列)中各元素与其路段单位流量权重乘积之和为

(1)

式(1)表示与第i个组团中的节点相连的权重路段在所有权重路段中所占的比例。其中wij=wji，在此基础上，定义模块度的衡量标准为

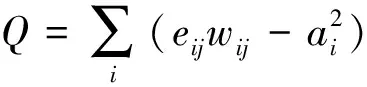
(2)

式(2)中：eij表示网络中连接两个不同组团间节点的路段在所有路段中占的比例；wij表示组团内部各路段的单位流量权重。

式(2)的物理意义是：网络中连接两个同种类型的节点的路段(即组团内部路段)的占比减去在同样的组团下任意连接这两个节点的路段的期望值。如果组团内部边的比例不大于任意连接时的期望值，则有Q=0。Q的上限为Q=1，Q越接近这个值，就说明网络的组团越明显。有研究表明，Q的最大值对应的组团就是网络的组团，且在实际网络中该值通常位于0.3～0.7。

模块度存在的意义在于，网络的组团划分时无法确定何时停止删除关键边，这样就无法判断它所得的组团是否是实际网络中的组团。因此，在算法中，同时计算模块度的值，当模块度值达到最大时，便停止删减关键边，并把模块度最大时的组团划分情况作为最后的组团划分结果。算法的基本流程如图2所示。

图2 WGN算法步骤Fig.2 Workflow of WGN algorithm

3 案例城市路网关键路段诊断

3.1 路网组团划分依据

选择武汉市武昌区作为研究对象，开展案例分析。由于武汉市是被长江、汉江分割的城市，形成了两江三片的格局。武昌、汉口、汉阳三个区镇之间，只能靠桥梁、隧道或者轮渡连接，桥梁、隧道承担主要的交通量，轮渡只承担少量的行人交通量，现有桥梁和隧道数目较少。因此，三镇形成了三个大组团，从路网结构的角度上看，将武昌区作为一个独立的研究对象是可取的。

在对武汉市主城区路网进行组团划分的过程中，将道路交叉口抽象为节点，交叉口间的路段抽象为边，根据《2020年版武汉市交通旅游图》，绘制出2020年武汉市主城区道路网络系统图。并且根据《武汉市骨架路网建设时序研究》中2020年骨架路网的建设时序图，及其他相关资料，将研究区域的交通网络按4个等级进行划分：快速路、主干路、次干路、支路。

根据《城市道路交通规划设计规范》等相关资料，整理后得到各类道路的车道数、设计车速及单车道设计通行能力如表1所示。以自由流时间作为网络边长的衡量标准，其中自由流时间由路段的长度与其设计速度的比值表示。

由表1中数据，把双向6车道快速路的通行能力转化为单位流量权重系数后作为标准，则其他道路相对单位流量权重系数如表2所示。

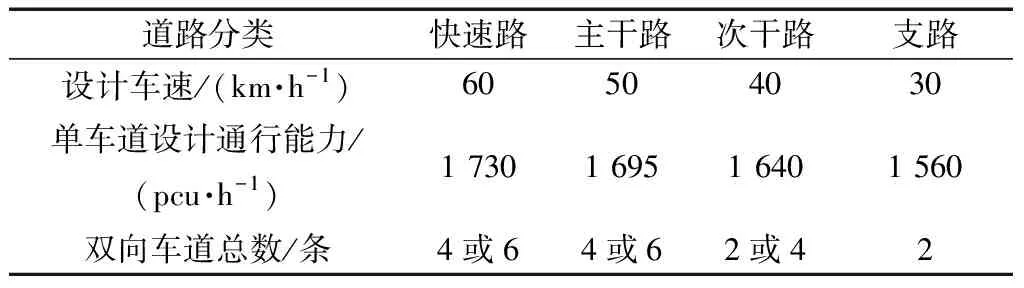
表1 各类道路特征

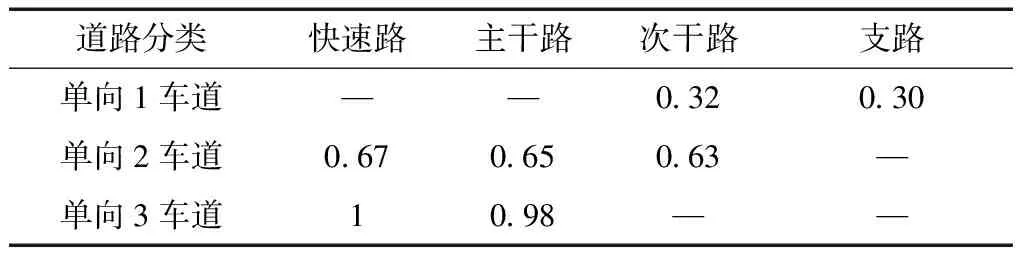
表2 单位流量权重系数

3.2 路网组团划分结果

3.2.1 武昌区路网组团划分

根据路网本身结构，用WGN算法对武昌主城区范围内的路网进行组团划分，得到以下结果：组团数9个，组团划分效果如图3所示。

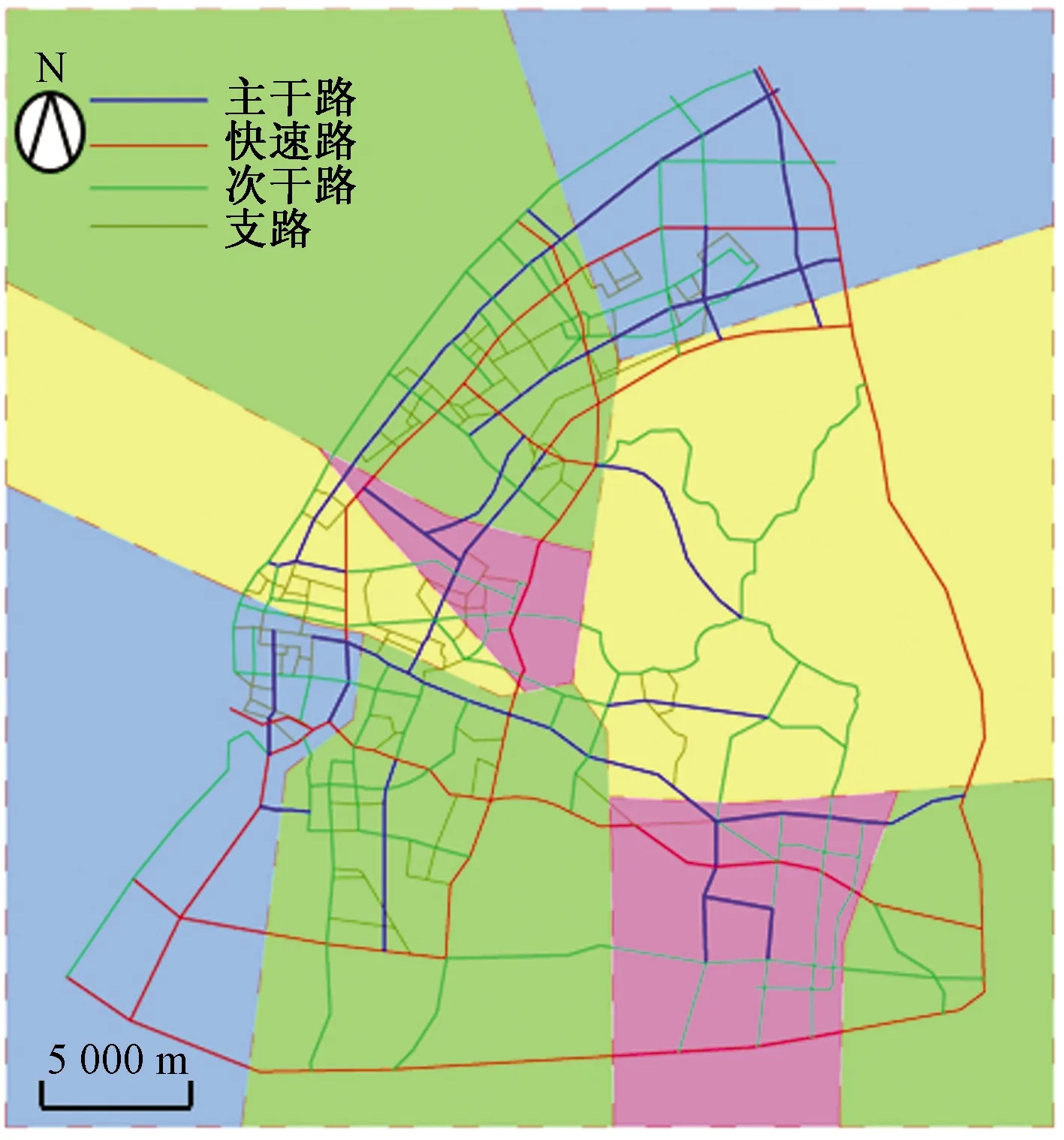
图3 武昌区路网组团划分效果图Fig.3 Grouping of Wuchang District road network

3.2.2 关键路段诊断结果

由算法原理可知，连接两个组团的路段数量远远少于组团内部的路段数量，因此组团间的连接路段，必定为关键路段。关键路段的存在，说明路网结构有不完善的地方，导致两个组团之间缺乏相当的连通度，所以，关键路段既是可能产生拥堵的路段。利用WGN算法，诊断出武昌主城区范围内的关键路段共有51条，如表3所示。

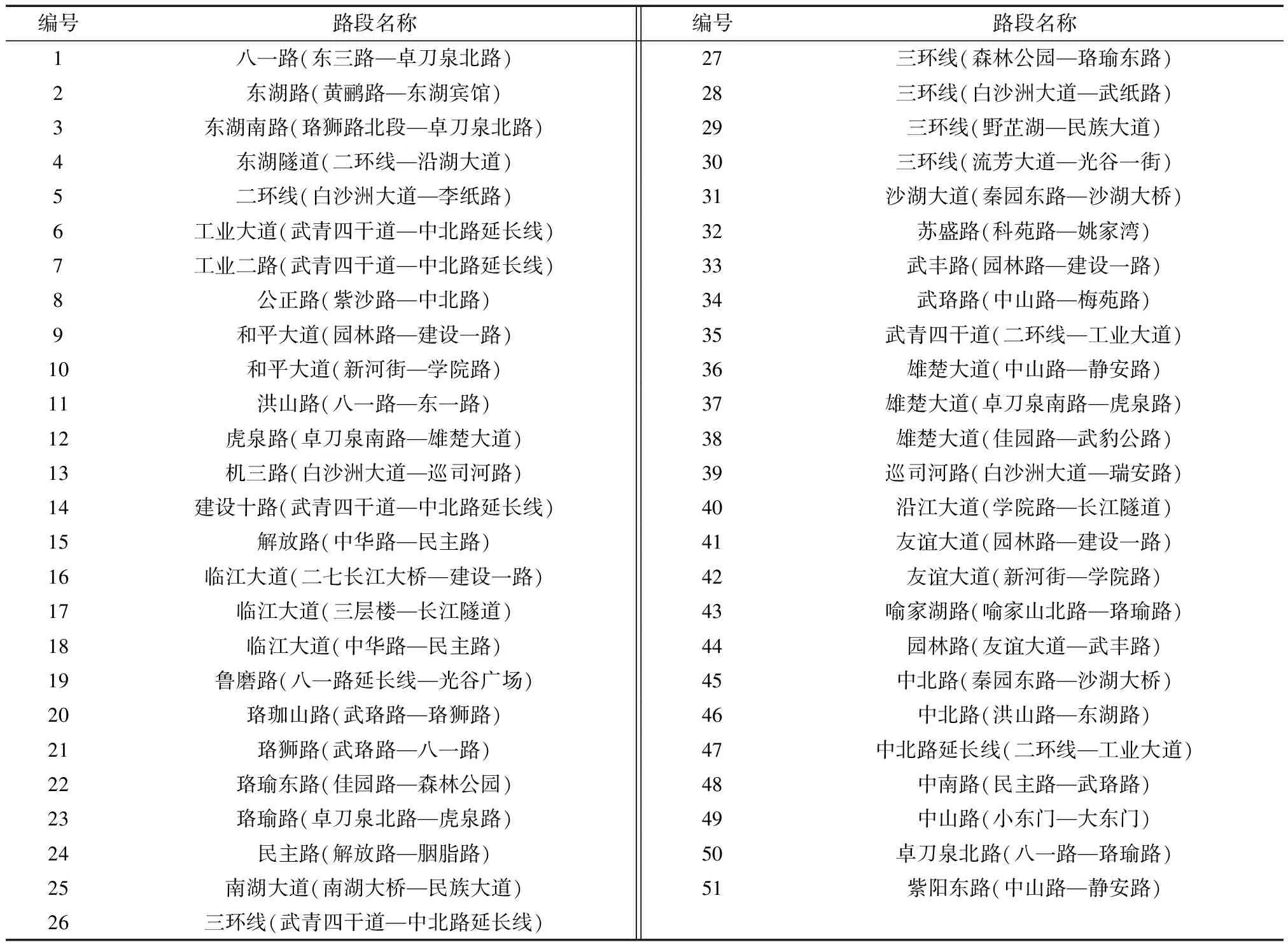
表3 武昌区关键路段诊断结果

4 考虑出行需求后的拥堵路段诊断

4.1 拥堵路段诊断原理

经过对城市道路网络进行组团划分，可以发现，城市道路网络结构中存在诸多问题，例如，组团之间连接路段过少，关键路段等级过低等。与此同时，在土地利用强度和功能分区的影响下，城市各区域交通出行的发生与吸引强度分布不均匀，进一步造成了部分路段交通流量过大，形成交通拥堵。

因此，在对武昌区道路网络结构问题进行分析诊断的基础上，对WGN算法进行了改进，将交通小区间的OD量作为权重，对路网中路段的介数值(作为最短路径的次数)进行加权计算，并根据路段加权之后的介数值判断其重要性。本方法除考虑路段在路网结构中的重要性外，同时考虑了路段在实际交通需求中的重要性，对诊断实际路网中的拥堵路段具有重要意义。

4.2 拥堵路段诊断模型与结果

4.2.1 拥堵路段诊断模型

设路网中每一个节点均是一个交通起止点，以路网中各路段自由流时间为判断依据，用BFS(breadth first search)算法，即广度优先搜索法搜索出路网中每对节点之间的最短路径。

(1)BFS算法搜索最短路径，将每对节点之间的最短路径记为三维数组Dij，最短路长度记为二维数组Sij，即

Dij=[i,j][i,…，x,…，j]

(3)

(2)计算每条路段的介数值bij，既每条路段作为最短路的次数。与组团划分模型不同的是，由于考虑每对节点之间的OD(出行需求)，因此，介数值bij要以最短路经过此路段的节点对之间的OD量为权重，即

bij=∑ODxy，节点对xy之间的最短路径Dxy经过路段ij

(4)

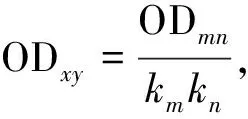
(3)找出介数值最大的路段max{bij}。

(4)删除介数值最大的边，同时，计算此时网络的模块度Q，即

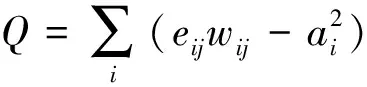
(5)

拥堵路段诊断步骤如图4所示。

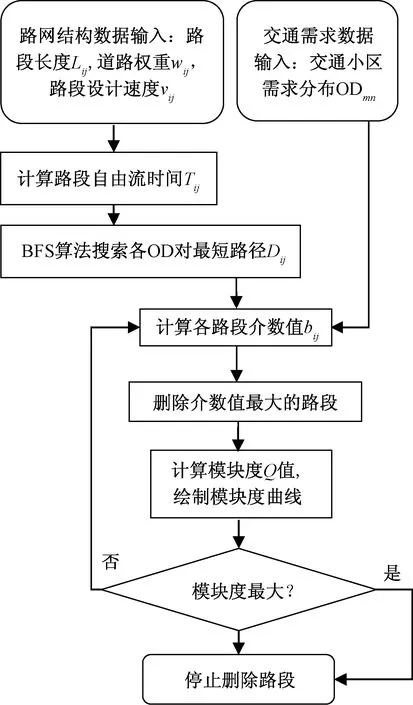
图4 拥堵路段诊断算法步骤Fig.4 Workflow of the congestion diagnosis algorithm

4.2.2 武昌地区拥堵路段诊断结果

按照上述方法，在充分考虑路段在路网中的重要性的基础上，同时考虑路段在交通需求中的重要程度，对武昌区路网进行拥堵路段分析，共诊断出拥堵路段14条，如表4和图5所示。

表4 武昌区拥堵路段诊断结果

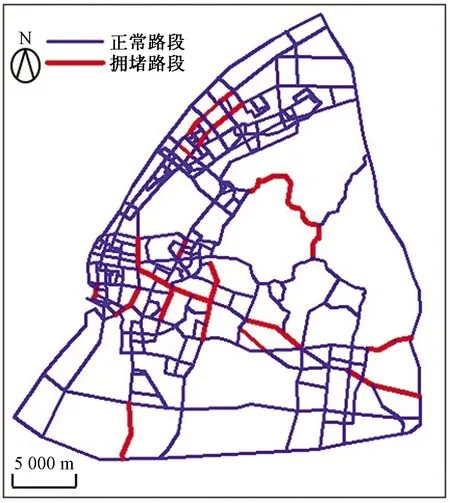
图5 武昌区拥堵路段示意图Fig.5 Congested road segments in Wuchang District

5 结论

主要从中观路网结构的角度，对武昌区的道路网络的供需情况进行诊断，研究主要结论如下。

(1)为了探究城市道路网络局部路段出现拥堵的结构性原因，找出现状路网、规划路网中可能发生拥堵的关键路段，首先对武昌区道路网络进行了组团划分，从而诊断出路网中的关键路段，即各组团之间的连接路段；而后考虑到城市中不同区域的居民出行需求的分布并不均匀，将居民出行OD加载到道路网络组团划分算法的最短路径计算中，从而诊断出路网中的拥堵路段。

(2)从组团划分的结果上看，武昌区路网结构存在一定问题：组团内部路网密度较大，连通度较好；各组团间，道路数量较少，缺乏一定的联通度。而组团间连接路段的数量与组团内部路段的数量之间较大的差异，造成了道路供给的不均衡现象，是形成道路拥堵的原因之一。

(3)诊断出的关键路段，即是可能发生拥堵的路段。在对武昌区现状路网的诊断中，发现了51条关键路段，这些路段是由于道路网络结构不合理而产生的瓶颈路段，然而由于不同路段交通需求不同，并非所有的关键路段都会产生拥堵现象。因此，在诊断出结构性关键路段的基础上，考虑了出行需求，发现了14条拥堵路段，这些路段即是最容易发生拥堵的路段。参考现实交通状况与相关资料，如《武汉市主要道口交通堵点疏解初步方案研究》等，通过对比发现，诊断出的部分关键路段和大部分拥堵路段在现实中确实是经常发生拥堵的路段。

(4)研究结果可以对规划路网的潜在问题做出预判，在可能的拥堵发生之前，及时采取措施，缓解拥堵。

(5)根据对现状路网进行诊断的结果，可以对关键路段进行分类，对于不同道路等级的关键路段，提出相应的优化措施：对于道路等级较低的关键路段，可以采用提高道路等级的方法；对于道路等级本身较高的关键路段，可以采取在附近修建平行路段，来增加相应组团的连通度。