块系岩体摆型波能量转化和耗散规律

朱守东， 戚承志*， 姜 宽， 于 航， 赵 发， 王晓娇

(1.北京建筑大学， 北京未来城市设计高精尖中心与城市基础设施建设北京市国际合作基地， 北京 100044； 2.北京工业大学建筑工程学院， 北京 100124)

能源安全作为国家稳定的“压舱石”之一，事关生产、人民生活和国防事业的建设。随着矿井等地下工程不断深向地下，冲击地压等工程灾害频发，以往积累的理论和实践经验与现实脱节，越来越无法满足工程实践需求。

Kurlenya等[1-3]和Oparin等[4]发现并验证了摆型波的存在，开辟出深部岩土力学研究的新领域。Aleksandrova等[5-7]提出了一维块系岩体摆型波传播动力模型，该动力模型在理论研究中被广泛采用。Saraikin等[8-11]将摆型波的理论研究拓展向二维，分析了摆型波传播的影响因素，并从理论上证明了二维岩体模型中同样会出现准共振现象。

中国科研学者也对摆型波进行了理论和实践研究。钱七虎[12]对深部岩体的构造层次、摆型波现象、超低摩擦现象、冲击地压产生机理等进行了研究总结。吴昊等[13-14]通过自主研发的深部岩体动态特性试验系统，研究了各种因素对摆形波传播的影响。潘一山、王凯兴等[15-17]研究了块体等级、块体间夹层性质对摆型波传播的影响，并利用摆型波的频域响应反演了块体间的黏弹性性质。潘一山等[18-19]基于摆型波的理论研究成果设计了新型防冲支护设计模型，改善了传统支护结构设计。姜宽等[20-22]研究了夹层非均匀性及夹层双模量特性对摆形波传播的影响，并研究了频域响应规律。

摆型波低频低速传播，并携带大的能量，易引发各种工程地质灾害，但以往关于摆型波的研究主要集中在块体的位移、速度和加速度的响应规律上，摆型波能量转化和耗散规律的研究还很不充分。王凯兴等[23]中研究了摆型波传播过程局部岩块与系统中弹性势能与动能转化的规律，研究了整个块系岩体的系统能量的耗散规律，理论分析过程中尚未考虑各种因素对弹性势能、动能和系统总能量的传递和耗散过程的影响。实际上，不同工程环境中，岩块的大小、岩体的破碎程度、岩块间裂隙或节理的力学性质都各有差异，这些差异在岩体的破坏及能量释放过程中起着重要作用，因此有必要研究刚度系数k、黏性系数c及块体尺度对摆形波传播过程中能量转化和耗散的影响。这些研究将加深我们对于深部块系岩体的动力学性质的了解，加深对于块系岩体摆型波能量转化和耗散规律的掌握，对预防工程灾害、保障工程安全具有重要意义。

1 摆型波传播模型与计算方法

1.1 摆型波传播动力模型

采用Aleksandrova[5]提出的等级块系岩体摆型波传播动力模型，如图1所示。

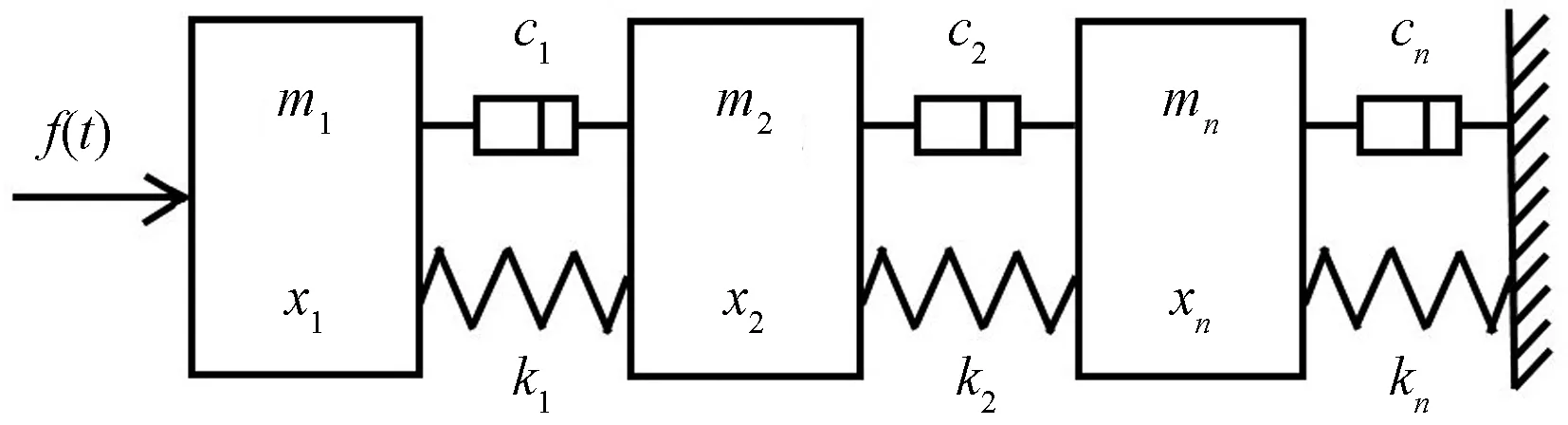
f(t)为冲击扰动；m为物块质量；c为黏性系数； k为刚度系数；x为物块状态图1 块系岩体摆型波动力模型Fig.1 Dynamic model of pendulum-type wave of block-rock

该理论模型由n个岩块和软弱夹层构成，岩块视作刚体，块体间软弱夹层简化为凯尔文黏弹性模型，冲击扰动f(t)作用在第一个块体上，最右侧为固定端。研究块体的受力情况，可推导出块系岩体系统的运动方程，即

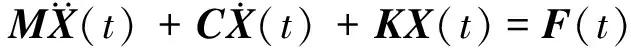
(1)

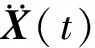
(2)

(3)

(4)

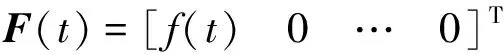
(5)

1.2 计算方法

本文中计算采用中心差分法。中心差分法是基于用有限差分代替位移对时间的导数的显式计算方法，计算量与自由度成线性关系，计算效率高。本文计算模型中块体个数较多，相较于传统方法，选用中心差分法可大大降低计算量。

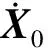
(6)

(7)

计算中选取的时间步长为Δt，总的步长数为Nt。将X(ti+1)和X(ti-1)分别在X(ti)处用泰勒级数展开，由于Δt取值足够小，忽略三阶及以上高阶项，可得

(8)

(9)

整理可得位移递推公式

(10)

(11)

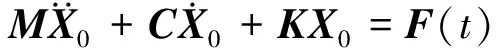
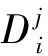
(12)

(13)

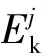
(14)

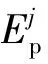
(15)

第Δt×j时刻n个块体的总能量能Wj为

Wj=Ek，j+Ep，j

(16)

中心差分法是有条件稳定的，且稳定条件为

(17)

为了能达到足够的精度，在一般的计算中，常用稳定验算条件为

(18)

在稳定验算条件中，T和ω分别为系统的自振周期和自振频率，当选取的时间步长过大或系统的自振周期过小时，中心差分法的稳定性将不再满足稳定条件。 自振周期与刚度有关，系统刚度越大，自振频率越大，自振周期越小，Δt/T也越小，因此当刚度系数最大时Δt/T取最大值，因此只需验证此时中心差分法的稳定性是否满足要求即可。本文计算过程中取用的Δt=0.000 1，最大刚度系数值为k=4×105kg/s2，当自由度为10，即块体个数为10时，可求得系统的自振频率由大至小分别为1 250.2、1 208.2、1 139.2、1 044.8、927.0、788.5、632.4、462.1、241.5、94.5 Hz，最大频率(基频)为1 250.2 Hz，此时Δt/T有最大值为0.02，小于稳定性数值0.1，因此本文采用中心差分法的稳定性满足要求。

2 刚度系数k对能量转化和耗散的影响

本节选用文献[7]中取用的参数，块体质量mi=1 kg，刚度系数ci=20 kg/s(i=1,2,…，10)，块体编号1～10。块系岩体受到扰动后的初始状态为：xi(0)=0(i=1,2,…，10);v1(0)=2m/s，vi(0)=0 m/s(i=2,3,…，10)。表述为：第一个块体初速度为2 m/s，初位移为0，其他9个块体初速度和初位移均为0。对刚度系数ki分别取k1=1×105kg/s2、k2=2×105kg/s2和k3=4×105kg/s2时的块体动力响应进行求解，得到冲击发生后0.3 s内每个块体及系统的动能、弹性势能和总能量。

2.1 刚度系数k对单个块体能量最值的影响

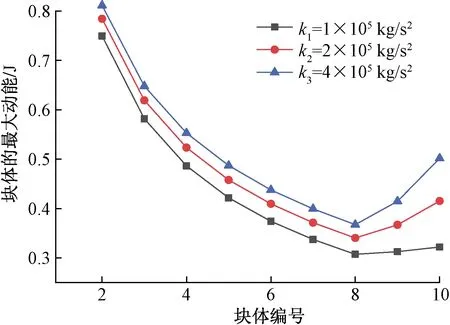
图2 不同刚度系数各个块体的最大动能图Fig.2 Maximum kinetic energy of blocks with different stiffness coefficients

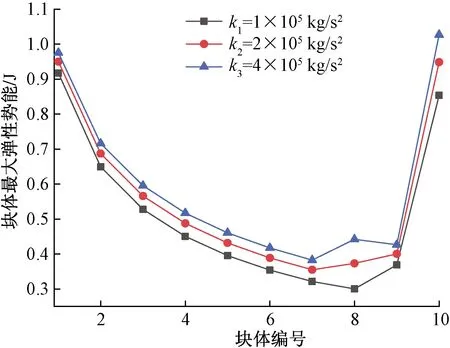
图3 不同刚度系数各个块体的最大弹性势能图Fig.3 Maximum elastic potential energy of blocks with different stiffness coefficients

由于第1个块体的动能即初始扰动能量2 J，且数倍于其他九个块体最大动能，为了直观清晰地展现动能的变化规律，图2仅列出第2～10个块体的最大动能。由图2可知，随着刚度系数的增大，每个块体的最大弹性势能均增大，印证了刚度系数k表征能量的传递。以k1=1×105kg/s2时为例，10个块体最大动能的出现时间分别为第0、0.055、0.092、0.127、0.160、0.194、0.227、0.259、0.400、0.408秒，块体距冲击点越远最大动能出现的时间越晚。第1～10个块体的最大动能呈现先减小后增大的趋势，由于阻尼的存在，摆型波传播过程中能量逐渐损耗，故前7个块体的最大动能逐渐减小，最右侧几个块体的运动受到固定端的影响较大，块体的最大速度增加，对应的最大动能增大。这种影响类似于波的反射。

弹性势能有着类似的变化规律，随着刚度系数的增大，每个夹层的最大弹性势能均增大。第1～10个夹层的最大弹性势能呈现先减小后增大的趋势，由于能量损耗，故前7个块体的最大弹性势能逐渐减小，最右侧几个夹层由于受到固定端的影响，块体间的最大相对位移变大，对应的最大弹性势能增大，第10个块体的最大弹性势能甚至超过第1个块体的最大弹性势能。

2.2 刚度系数k对块体系统能量转化和耗散的影响

冲击发生后0.3 s内块体系统动能、弹性势能和总能量分别如图4～图6所示。

系统的初始扰动能量为2.0 J，即系统能量的最大值。据图4和图5可知，系统动能和弹性势能均呈现周期性衰减，随着刚度系数的增大，动能和弹性势能的衰减周期均减小。三组数值模拟试验中系统弹性势能的最大值分别为1.13、1.24、1.34 J，随着刚度系数的增大，系统的最大弹性势能也增大。总体来看，刚度系数不影响系统动能和弹性势能衰减速度。图6中三条总能量衰减曲线基本重合，均呈指数衰减，衰减主要集中在冲击发生后极短时间内，刚度系数的改变不影响系统总能量衰减速度。

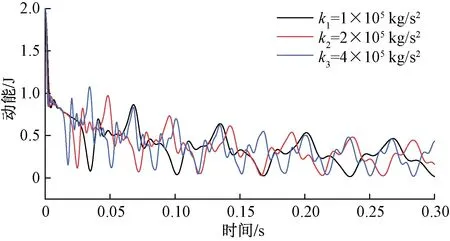
图4 不同刚度时动能衰减图Fig.4 Kinetic energy attenuation for different stiffness

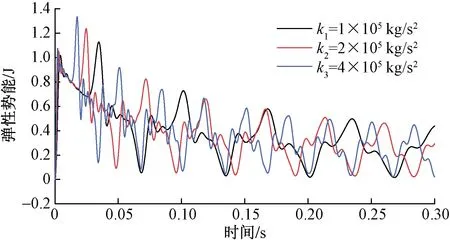
图5 不同刚度时弹性势能衰减图Fig.5 Elastic potential energy attenuation for different stiffness

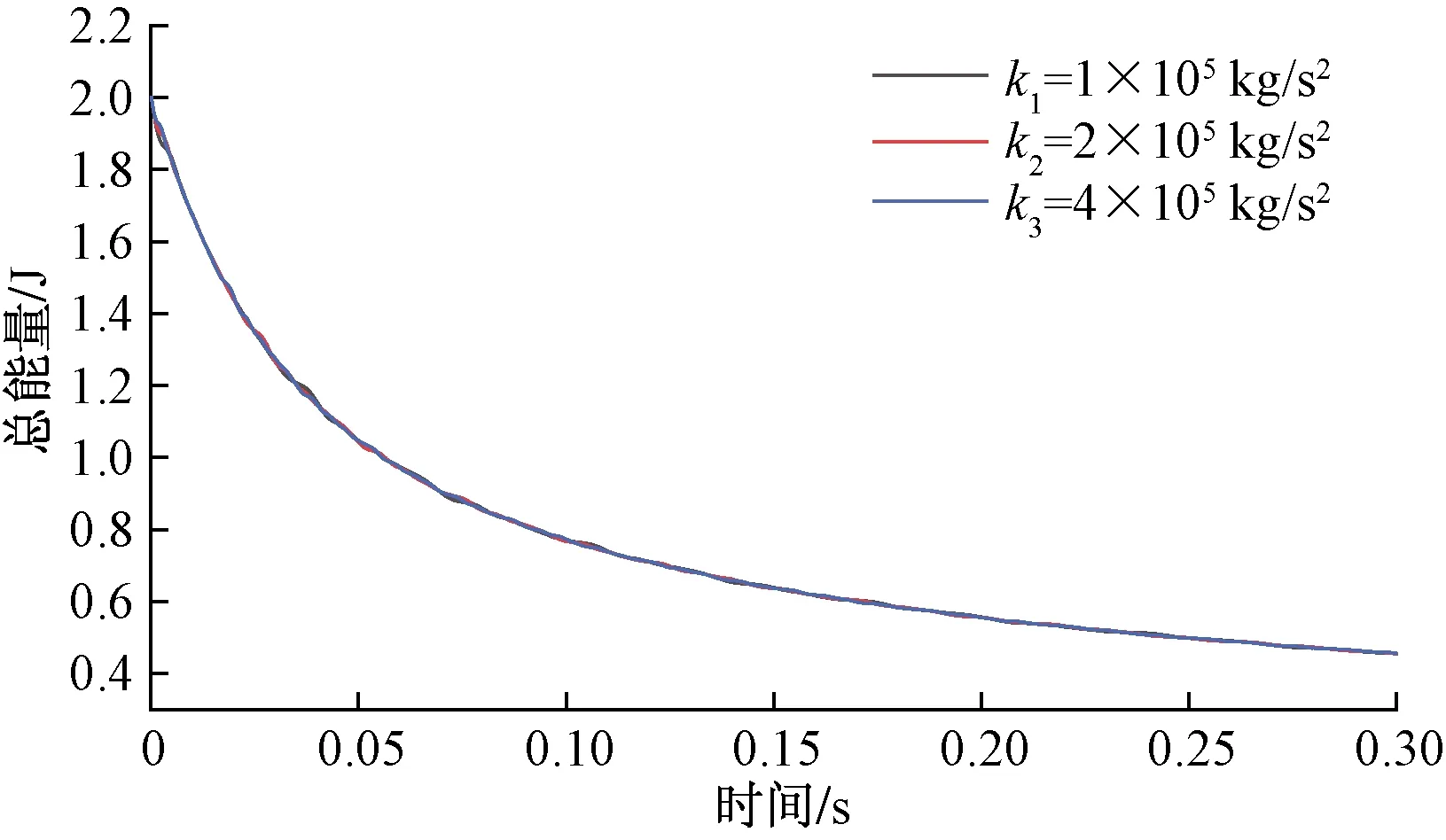
图6 不同刚度时总能量衰减图Fig.6 Total energy attenuation for different stiffness

3 黏性系数c对能量转化和耗散的影响

本部分选用的计算参数：块体质量mi=1 kg，刚度系数ki=2×105kg/s2(i=1,2,…，10)，块体编号1～10。块系岩体受到扰动后的初始状态为：xi(0)=0(i=1,2,…，10),v1(0)=2 m/s，vi(0)=0(i=2,3,…，10)。表述为：第1个块体初速度为2 m/s，初位移为0，其他9个块体初速度和初位移均为0。对黏性系数c分别取c1=10 kg/s、c2=20 kg/s和c3=40 kg/s时的块体动力响应进行求解，得到冲击发生后0.3 s内每个块体及系统的动能、弹性势能和总能量。

3.1 黏性系数c对单个块体能量最值的影响

冲击发生后0.3 s内各个块体的动能和弹性势能的最大值分别如图7和图8所示。

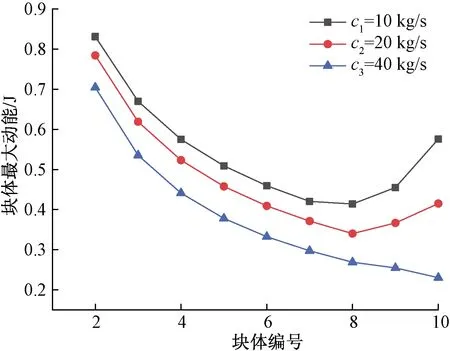
图7 不同黏性系数时各个块体的最大动能图Fig.7 Maximum kinetic energy diagram of blocks with different viscosity coefficients

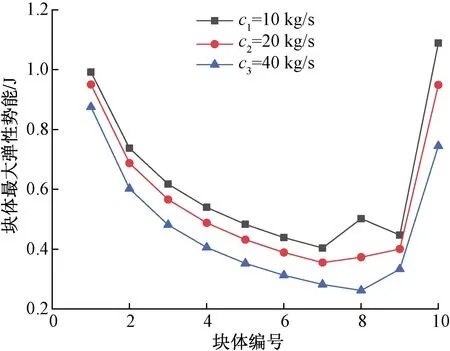
图8 不同黏性系数时各个块体的最大弹性势能图Fig.8 Maximum elastic potential energy diagram of blocks with different viscosity coefficients

图7同样只列出第2～9个块体的最大动能。

由图7可知，随着黏性系数的增大，每个块体的最大弹性势能均减小，印证了黏性系数c表征能量的损耗，黏性系数越大损耗越强。黏性系数为10 kg/s和20 kg/s时，第1～10个块体的最大动能呈现先减小后增大的趋势。黏性系数为40 kg/s时，第1～10个块体的最大动能依次逐渐减小。可见，黏性系数较大时，固定端对最右侧几个块体的动能影响较小。

由图8可知，随着黏性系数的增大，每个夹层的最大弹性势能均减小，第一个夹层到第十个夹层的最大动能先减小后增大，同样是能量逐渐损耗和固定端效应综合影响的结果。

这是我的第一部长篇小说，成稿于十多年前。动笔写它时我还没有文学梦想，以至于成稿很多年都没有投稿。偶然从一个群里看到有出版商征稿，没顾忌人家只要前五章的要求，就把全稿投了过去。投完许久都没动静，直到出版合同寄来，我才相信可以不花钱正规出版。

3.2 黏性系数c对块体系统能量转化和耗散的影响

冲击发生后0.3 s内块体系统动能、弹性势能和总能量分别如图9～图11所示。

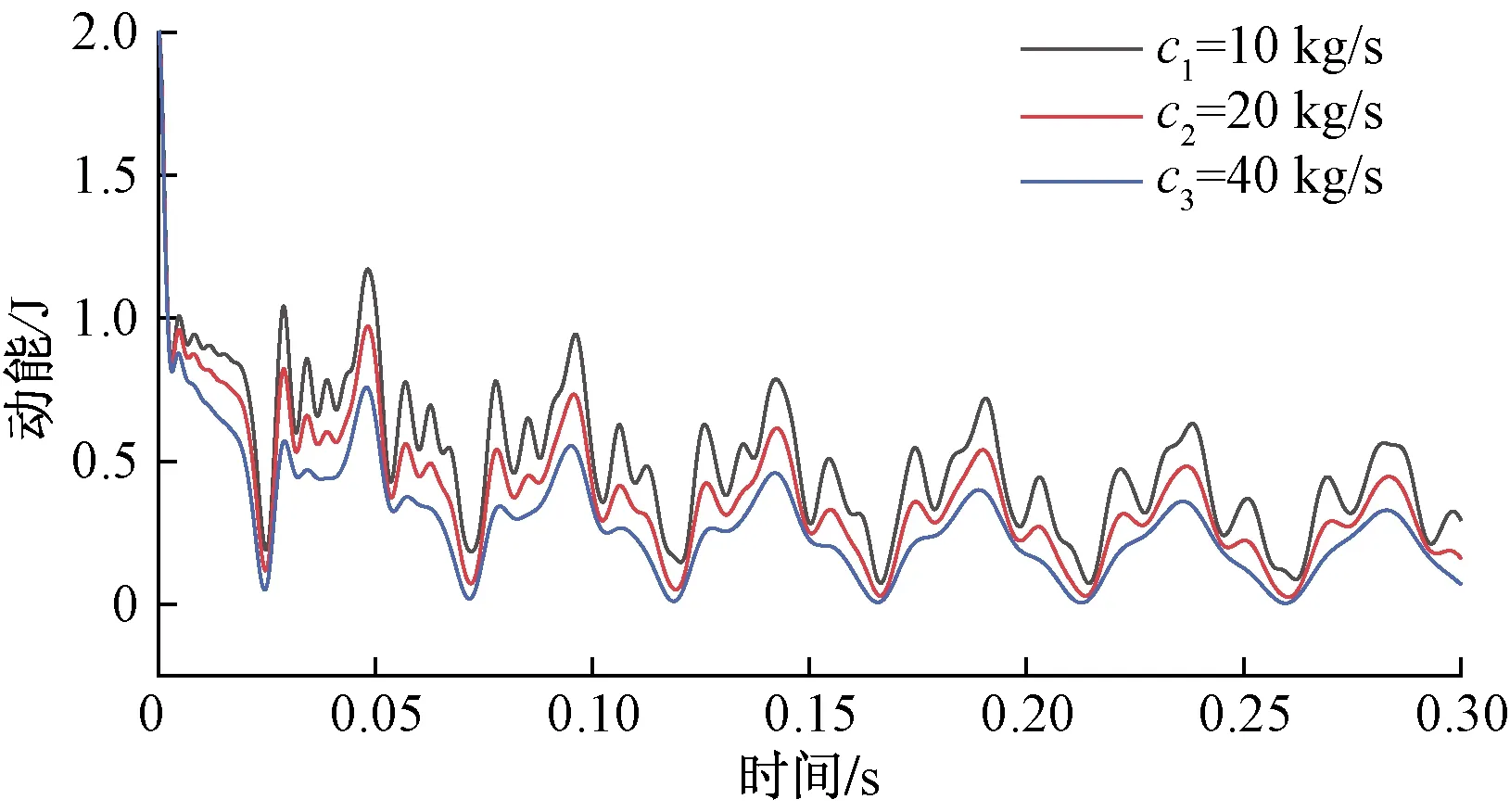
图9 不同黏性系数时动能衰减图Fig.9 Kinetic energy attenuation for different viscosity coefficients

图10 不同黏性系数时弹性势能衰减图Fig.10 Elastic potential energy attenuation for different viscosity coefficients

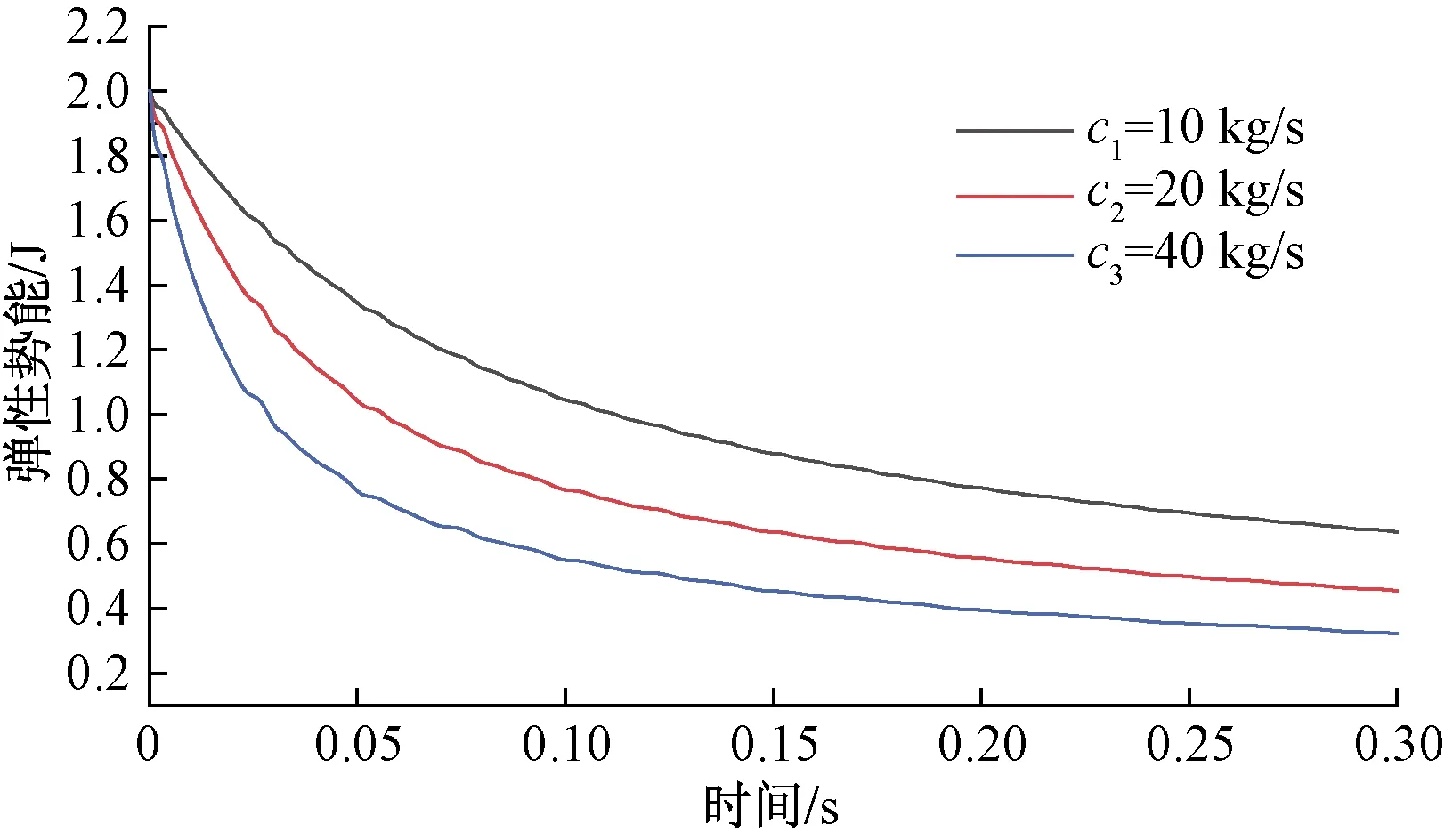
图11 不同黏性系数时总能量衰减图Fig.11 Total energy attenuation for different viscosity coefficients

据图9和图10可知，系统动能和弹性势能均呈现周期性衰减，随着黏性系数的增大，动能和弹性势能的衰减周期基本保持不变，每个衰减周期内的能量峰值均显著降低，系统动能和弹性势能衰减速度变快。三组试验中系统弹性势能的最大值分别为1.42、1.24、1.01 J，随着黏性系数的增大，系统的最大弹性势能减小。

图11显示了黏性系数c分别为c1=10 kg/s、c2=20 kg/s、c3=40 kg/s时的总能量衰减曲线。系统的初始扰动能量为2.0 J，即系统能量的最大值。为了表征能量变化的快慢，特引入能量变化率，用ΔE/Δt表示。系统能量变化率越小，能量的衰减就越快。c1=10 kg/s时，在 0.05 s末系统能量为1.34 J，ΔE/Δt=-13.2 J/s，系统能量已衰减33%；c2=20 kg/s时，在0.05 s末系统能量为1.04 J，ΔE/Δt=-19.2 J/s，系统能量已衰减48%；c3=40 kg/s时，在 0.05 s末系统能量为0.76 J，ΔE/Δt=-24.8 J/s，系统能量已衰减62%；在冲击发生后很短时间内即完成大部分的能量衰减，总能量随着黏性系数增大，系统能量变化率显著增大，总能量前期衰减变快。

4 块体尺度对能量转化和耗散的影响

Sadovsky[24]提出了深部块系等级构造理论，认为深部岩体由不同等级的具有自相似特性的块体组成。文献[25]中给出了等级块系岩体的尺寸计算公式为

(19)

式(19)中：Δi与Δ0分别表示等级为i和0的块体的尺寸，并由此得到两者之间的序列关系。由于块体视为均质，因此质量之比即为体积之比。同等规模的岩体系统，当裂隙较多且发育比较充分，岩体破碎程度较高时，块体体积小而等级较高；当岩体整体性较好，裂隙少且未全部贯通时，块体体积大块体等级较低。

4.1 块体尺度对单个块体能量最值的影响

冲击发生后0.4 s内三个等级块体系统内的各个块体的动能和弹性势能的最大值分别如图12和图13所示。

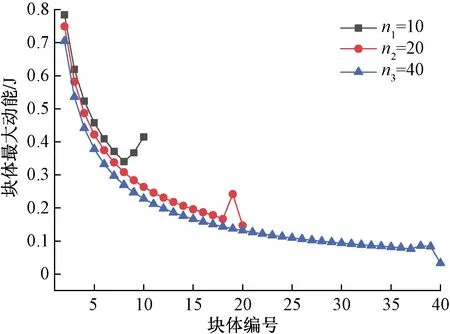
图12 不同等级各个块体的最大动能图Fig.12 Maximum kinetic energy of each block of different grades

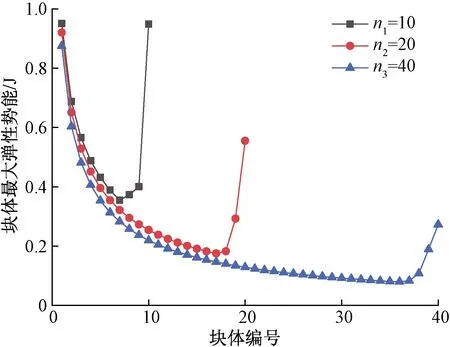
图13 不同等级各个块体的最大弹性势能图Fig.13 The maximum elastic potential energy of each block of different grades

图12同样不再列出第1个块体的最大动能。由图12可知，块体等级越低，相对应的最大动能和弹性势能均越高，块体系统处在较高的能量状态。由于阻尼的存在，能量逐渐消耗，故越往后最大能量值越低，当块体尺度较小时，夹层数目更多，因此能量衰减得越快，相对应的最大动能和弹性势能均减小得越快。

图12和图13对比来看，靠近固定端的块体的最大动能有所增加，但是增加的幅度较小，而靠近固定端的块体最大弹性势能增量及其显著，第10个块体的最大弹性势能甚至超过第1个块体的最大弹性势能。总体来看，固定端对于弹性势能的影响要远大于对动能的影响。

4.2 块体尺度对块体系统能量转化和耗散的影响

冲击发生后0.4 s内块体系统动能、弹性势能和总能量分别如图14～图16所示。

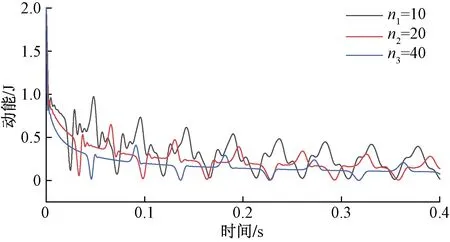
图14 不同块体等级动能衰减图Fig.14 Kinetic energy attenuation for different block levels

图15 不同块体等级弹性势能衰减图Fig.15 Elastic potential energy attenuation for different block grades

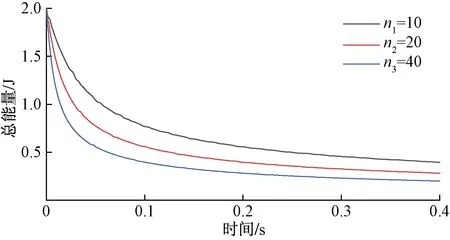
图16 不同块体等级总能量衰减图Fig.16 Total energy attenuation for different block grades

由图14和图15可知，系统动能和弹性势能均呈现周期性衰减，随着块体等级的增大，动能和弹性势能的衰减周期变大，衰减周期的能量峰值显著降低，系统动能和弹性势能的转化周期变大、衰减速度明显变快。三组数值模拟试验中系统弹性势能的最大值分别为1.24、1.02、0.98 J，随着块体等级的变大，系统的最大弹性势能减小。

原岩体在 0.05 s末系统总能量为1.04 J，系统能量已衰减47.9%，ΔE/Δt=-20.8 J/s。等级为2的岩体在 0.05 s末系统能量为0.77 J，系统能量已衰减61.3%，ΔE/Δt=-24.5 J/s。等级为4的岩体在0.05 s末系统能量为0.56 J，系统能量已衰减72.2%，ΔE/Δt=-28.9 J/s；块体等级越高，尺度越小，扰动后初始时刻总能量的衰减速度越快，随后衰减速度变慢并趋于一致。相同体积的岩体系统，单个块体体积减小而数量增多，对应的软弱夹层的数量也增多，摆型波传播过程中遇到的阻碍就越多，因此能量耗散的效率更高，能量在极短时间内完成耗散。

5 结论

(1)在振动过程中，伴随着块体间的相对位移，夹层被拉伸或压密，弹性势能赋存其中，软弱夹层是块体间能量传递的媒介；冲击发生后，系统动能和弹性势能均呈现周期性衰减，两者不断转化，基本呈反相。

(2)刚度系数影响系统动能和弹性势能的衰减周期，刚度系数越大，系统动能和弹性势能的衰减周期越小，系统的最大弹性势能也越大。黏性系数影响系统动能和弹性势能的衰减速度，黏性系数的越大，每个衰减周期内的峰值显著降低，系统动能、弹性势能及总能量衰减速度变快，系统的最大弹性势能减小，动能和弹性势能的衰减周期基本保持不变。

(3)随着块体等级的增大，动能和弹性势能的衰减周期变大，即系统动能和弹性势能的转化周期变大，每个衰减周期的能量峰值均显著降低，同时，系统总能量在前期的衰减速度变快。

(4)受到固定端的影响，靠近固定端的块体的最大动能和最大弹性势能会有所增加，且最大弹性势能增加的幅度远大于动能增加的幅度。

研究了单一因素改变时，块系岩体摆型波动能、弹性势能和总能量转化和耗散的规律。但实际工程环境中，由于多重因素的共同作用，能量转化和耗散问题要复杂得多，还需要更详细的研究。