基于遗传算法考虑附加荷载刚性挡墙被动土压力计算

谢晓鹏, 窦国涛*, 王 娟, 高 波, 张志勇

(1.郑州航空工业管理学院土木建筑学院, 郑州 450046； 2.郑州大学水利科学与工程学院,郑州 450001； 3.江苏省交通工程集团有限公司, 镇江 212100; 4.中冶京诚工程技术有限公司, 北京 100176)

目前,工程上对于挡土墙或支护结构上的土压力的计算大多采用朗肯土压力理论或库伦土压力理论,两者均认为墙后填土破裂面形状是直线形式,然而不少学者研究表明墙后填土破裂面为曲线形式,如美国太沙基在30年代进行的试验研究、苏联索科洛夫斯基的松散介质极限平衡理论等[1-3]。Blum[4]、Soubra等[5]、Rieree等[6]和Benmebarek等[7]采用数值模拟方法研究了土体运动破坏的滑裂面；Meksaouine[8]、Ducan等[9]进行了相关的试验研究,不同程度引证出填土破裂面的曲线特征；杨贵等[10]以无黏性填土挡墙为研究对象,假设在考虑土拱效应时,极限状态下墙后土体的滑裂面为曲线,基于水平微分单元法推导出平动模式下挡土墙主动土压力的分布；杨明辉等[11]开展了刚性挡墙平动变位模式情况下墙后有限宽度土体破坏试验,试验结果表明,在墙后填土宽度较小情况下,土体破坏面为通过墙踵及某一固定点的曲面,由此基于变分极限平衡法,推导出滑裂面曲线的具体方程式为对数螺旋曲线。

针对附加荷载对土压力影响的研究,张军等[12]研究了在交通荷载作用下,拱涵土压力的变化规律；赵中源等[13]研究了仰斜式挡土墙平移(简称“T”)模式下，墙后填土不同荷载作用下土压力变化规律,建立挡土墙在T模式下墙背土压力计算模型,但未研究滑裂面的影响；王广月等[14]从明德林解出发, 结合朗肯土压力理论, 推导了挡土墙后填土内部受竖向局部均布荷载作用时, 挡土墙附加土压力计算公式；李建国等[15]介绍了均布矩形荷载作用下考虑土体各向异性的附加应力计算公式,编制了相关程序计算了各种不同情况下的附加应力系数,并与各向同性情况下的附加应力系数进行了对比；刘泽等[16]研究了路面车辆在挡土墙上引起附加土压力的分布规律,结合330国道莲都—缙云段改扩建工程中悬臂式 挡土墙的施工,在挡土墙的底板上方和立板内侧埋设了一系列的土压力盒,以工地施工用30 t自卸式货车为荷载源, 采用定点停车方式加载,测试了路面车辆荷载 (静载)引起的附加竖向和侧向土压力。

针对填土面倾斜对土压力影响的研究,陈陆望等[17]基于数学方法对斜单元体进行力和力矩的平衡分析, 得到了墙背粗糙且填土坡面倾斜情况下的土压力解析解, 并进一步分析了墙土之间摩擦角及填土坡面倾角对土压力的影响。上述研究中未考虑到滑裂面形状对土压力的影响。

目前,在岩土工程界中,一种源于自然进化的遗传算法(genetic algorithm,GA)也取得丰富的研究成果。王军[18]针对土质边坡滑裂面的特点,分析了遗传优化算法在边坡滑动面搜索和稳定性评价的有效性和合理性，通过改编的简易遗传算法程序对高陡土质边坡进行计算；张晓龙等[19]以弓长岭大阳沟排土场为例,借助极限平衡法获取研究所需数据,利用神经网络建立边坡坡角、单段台阶高度及相应的安全系数间的非线性关系,并以此关系式为边界约束条件,建立了优化边坡几何参数的数学模型,利用遗传算法和传统优化算法进行寻优；赵同彬等[20]在对破裂面上滑动土体静力极限平衡分析的基础上,建立了基于优化方法求解无黏性土、黏性土库仑土压力的自变量取值区间和目标函数模型,并采用遗传进化方法进行了实例求解分析,但其墙后填土破裂面为直线形式；Dou等[21]针对砂土填料墙体转动模式下非极限被动土压力,采用遗传算法进行了求解。将计算库仑土压力的问题可以归结为求解一个目标函数极值的优化问题,遗传算法在求解函数极值中不需要函数满足连续可微、凸性等条件,也不必对目标函数进行求导,只需在可行解域内进行编码、选择、交叉、变异等操作,就可以得到目标函数的极值。笔者前期进行了相关的土压力试验[22],在此基础上,拟基于对数螺旋组合面原理,在图解法中加入了附加荷载及填土面倾斜的影响,同时基于遗传算法进行了被动土压力的求解公式推导。

1 作图法求解被动土压力

1.1 考虑均布荷载工况

文献[23]中针对对数螺旋线组合面采用作图法来求解被动土压力,计算中未考虑均布荷载的工况,本节将针对此工况进行求解。

挡土墙后的土体滑裂面由两部分组成,一部分是由对数螺旋线BE,另一部分是直线EC,如图1所示。在求解被动土压力时,主要步骤如下。

步聚1如图1(a)所示,在挡土墙顶点A处作直线AD,直线AD与水平线AK的夹角为45°-φ/2,其中φ为土体的内摩擦角。在直线AD上任选一点O作为对数螺旋线中心点,以OB的长度r0,画对数螺旋线,对数螺旋线半径r=r0eθtanφ，其中θ为对数螺旋线的转角，螺旋线和直线AD相交于E点,过点E作EC线和AK线相交于点C,使得EC线和AC线角度为45°-φ/2。

步聚2如图1(b)所示,画出挡土墙后填土的受力图,其中G1为△EFC土体的重力；q为附加均布荷载；Q1为边FC均布荷载的合力,和边AF上均布荷载的合力Q2相等;G2为多边形ABEF土体的重力；R1为滑动面EC上的反力；R2为滑动面BE上的反力；C1为滑动面EC上的黏聚力；C2为滑动面BE上的黏聚力；Pp为被动土压力。

步聚3如图1(c)所示,按一定比例作竖直线ab,ab的长度为G1+Q1,过b点作bc线平行于EC线,bc线长度为EC线上黏聚力合力,过c点作斜线平行于R1,过a点作斜线平行于Pp,两线交于d点。

步聚4如图1(d)所示,按一定比例作竖直线mg,mg的长度为G2,G2=Q1+G1+g1+g2, 过g点作gh线平行于P,gh的长度为P,过h点作hj线平行于C2,hj的长度为C2,过j点作斜线jk平行且等于R2,过k点作斜线km和竖直线mg的夹角为90°-α+δ(α为挡墙墙背倾角,δ为墙体与土体外摩擦角),则线段km的长度则为螺旋曲线中心O时作用在墙面上的被动土压力Pp。

图1 附加荷载工况下被动土压力计算Fig.1 Calculation of passive earth pressure under additional load condition

步聚5如图1(e)所示,在AD线上选择点O1～O6,作竖直线分别和直线AK相交于O′1～O′6，按照步骤1～步骤4求出Pp1～Pp6,按一定比例尺分别在O′1～O′6,上作竖直线,其长度为Pp1～Pp6,并将其连成光滑的曲线,作水平线MN与mn曲线相切,得切点a,过a点向下作竖直线ab交AK于b点,则ab的长度按照前面所设比例尺进行转换,则可得挡土墙背后的被动土压力Pp。

1.2 填土面倾斜转化为集中荷载工况

文献[23]针对对数螺旋线组合面采用作图法来求解被动土压力,计算中未考虑填土面倾斜的工况,考虑此工况进行求解。

(1)如图2(a)所示,墙后填土面倾斜,和水平面夹角为ξ,在求解被动土压力时,主要步骤和均布荷载工况类似,不同之处如下。

(2)将土体ANF简化为集中荷载G3,加载于土体AFE上；将土体NFCM简化为集中荷载G4加载于土体EFC上；将边界MC所承受黏聚力C3和土体反力R3下移至边界EC上,如图2(b)所示。

(3)如图2(c)中,按一定比例作竖直线ab,ab的长度为G1+G4,过b点作bc线平行于EC线,bc线长度为EC线上黏聚力合力C1+C3,过c点作斜线垂直于EC,大小为R1+R3,过a点作斜线平行于Pp,两线交于d点。

(4)如图2(d)所示,按一定比例作竖直线mg,mg的长度为G2+G3+g1+g2。

(5)如图2(e)所示,则可得挡土墙背后的被动土压力Pp。

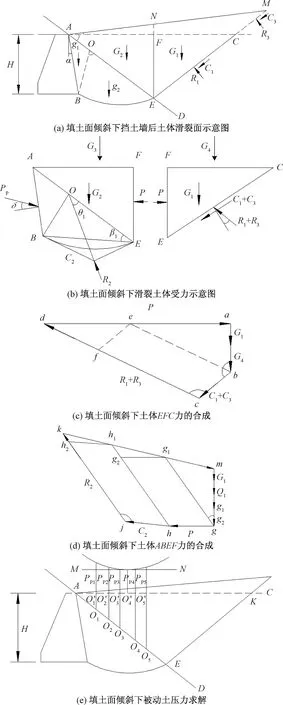
图2 填土面倾斜工况下被动土压力计算Fig.2 Calculation of passive earth pressure under sloping filling surface condition

2 基于遗传算法求解被动土压力

2.1 考虑均布荷载工况目标函数

图1中，角度及线段长度为

(1)

(2)

∠AOB=π-θ

(3)

(4)

(5)

(6)

(7)

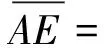
(8)

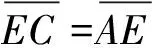
(9)

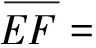
(10)

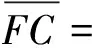
(11)

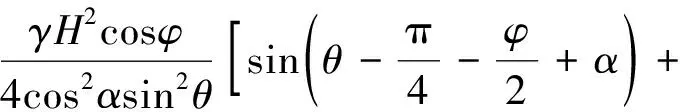
(12)

(13)

式(13)中：q为附加均布荷载，kN/m；Q1和Q2为等代荷载，kN。

土体ABEF的重力,可分为：土体AEF的重力,(G1相等)、土体ABO的重力g1和对数螺旋面积的重力g2,即

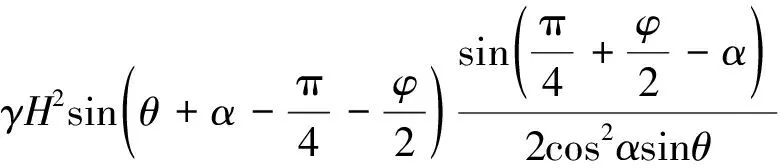
(14)

(15)

C1为直线滑裂面EC的黏聚力,则有

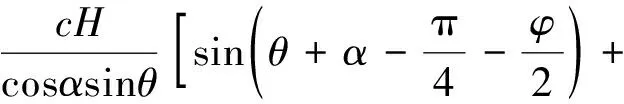
(16)

C2为对数螺旋线BE的黏聚力,则有

(17)

式中:c为黏土的黏聚力。

(18)

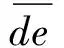
(19)

(20)

(21)

(22)

则有

(23)

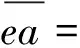
(24)

被动土压力Pp可表示为

(25)

图1(d)中角度分别为

∠h2kh1=∠g2h1g1=∠mg1g=

(26)

∠kh2h1=π-θ1-β1

(27)

(28)

(29)

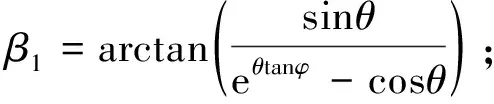
利用三角形正弦定理可求得

(30)

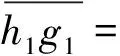
(31)

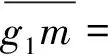
(32)

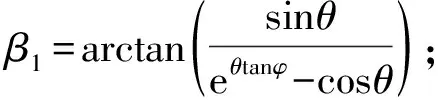
2.2 填土面倾斜转化集中荷载工况目标函数

图2中角度及线段长度为

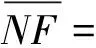
(33)

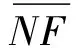
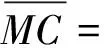
(34)

G3为土体ANF的重力,则有

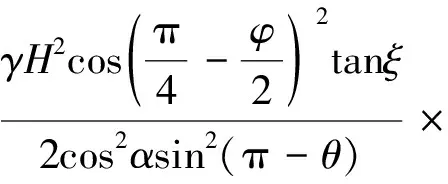
(35)

G4为土体NFCM的重力,则有

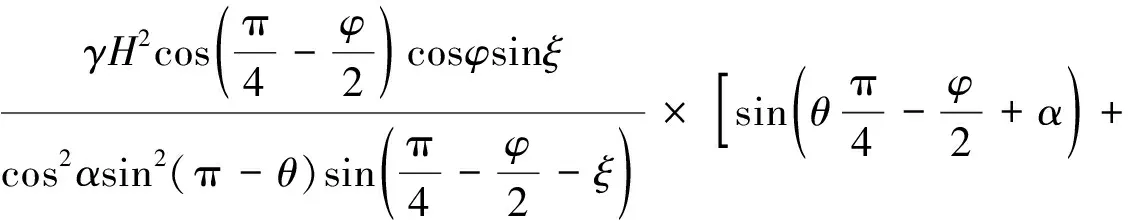
(36)

C3为直线滑裂面MC的黏聚力,则有

(37)

(38)

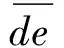
(39)

(40)

被动土压力Pp的表达式为

(41)

利用三角形正弦定理可求得

(42)

(43)

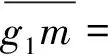
(44)

2.3 遗传算法求解

根据文献[23]可知,此被动土压力为所画弧线的最低点,则为最小值问题,采用适值函数标定的遗传算法进行求解,对于最小值问题,通常将其转换成最大值问题,将目标函数取反作为适值函数。遗传算法计算流程如图3所示。其求解程序为:[xv,fv]=NormFitGA(@fitness,x1,x2, 50, 500, 2, 0.9, 0.9, 0.04, 0.01),程序中xv为自变量,表示对数螺旋线角度θ；fv为因变量,表示所求被动土压力Pp;x1和x2表示遗传算法的界限。

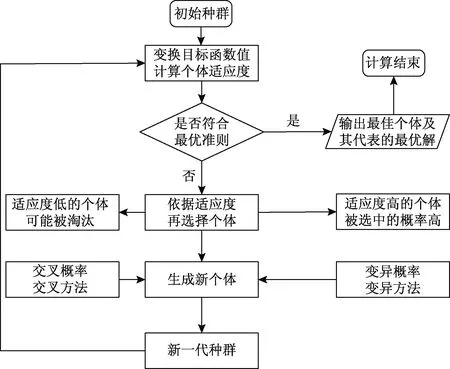
图3 遗传算法计算流程Fig.3 The calculation process of genetic algorithm

3 算例

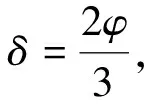
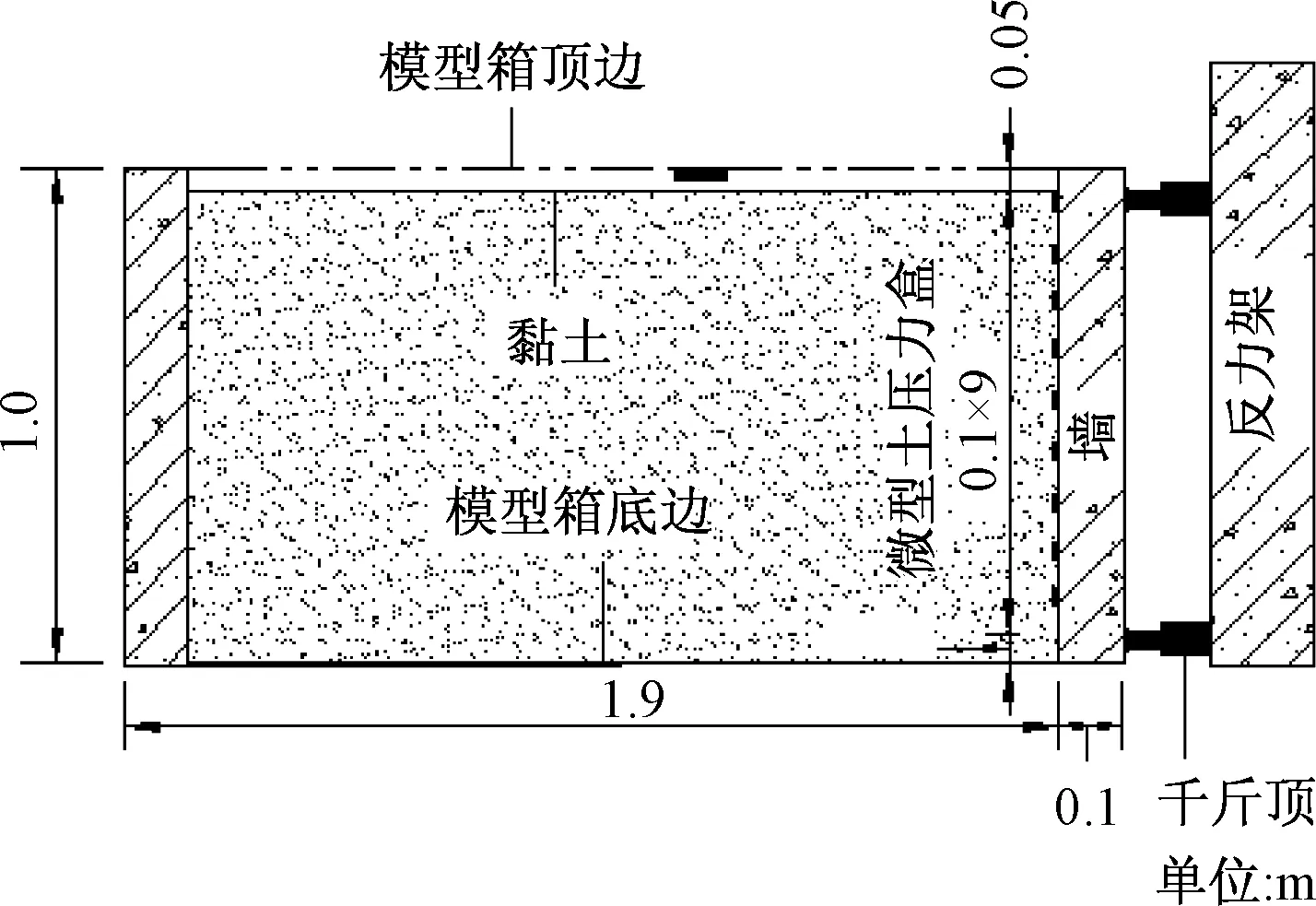
图4 模型箱示意图Fig.4 Model test device

图5 土压力计布置Fig.5 Location of earth pressure gauge

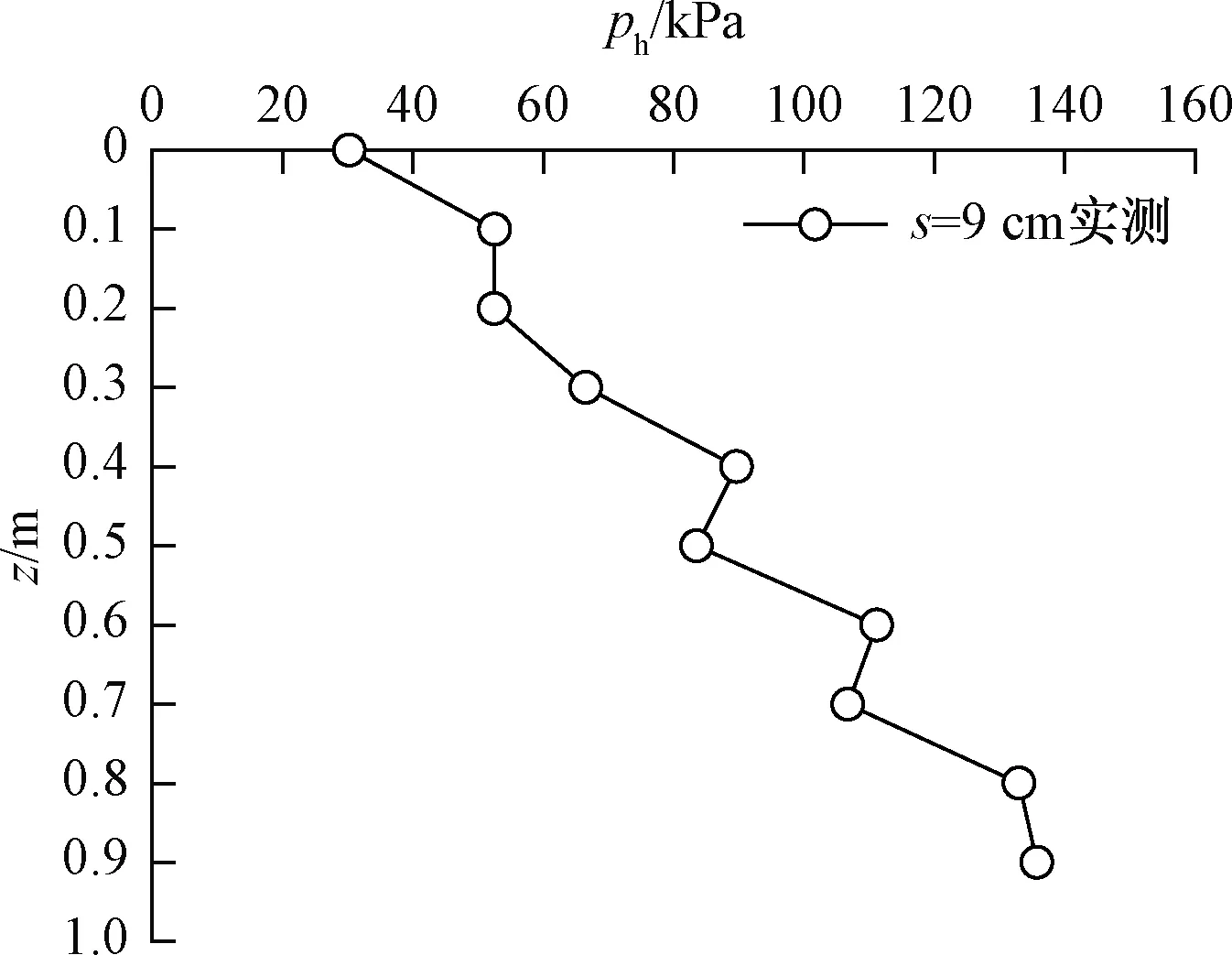
ph为侧土压力；z为墙体测点土中深度； s为墙体挤压土体位移。图6 被动土压力随深度分布Fig.6 Distribution of passive earth pressure along the depth

3.1 工况一

在本算例中,附加荷载q=0,然后分别采用作图法、遗传算法进行计算土压力合力计算,并和试验进行对比,结果如表1所示。比较作图法与遗传算法比值为1.023,两者接近,但作图法过程十分烦琐,遗传算法计算结果与试验值比较,误差为3.3%,和试验值接近。

3.2 工况二

在本算例中,将0～0.1 m深度的土体视为附加荷载,经换算q=1.573 kN/m,计算模型如图7所示,然后分别采用作图法、遗传算法进行计算剩余墙体0.85 m范围土压力合力,并和试验进行对比,如表1所示。比较作图法与遗传算法比值为1.035,两者接近,但作图法过程十分烦琐,遗传算法计算结果与试验值比较,误差为1.4%,和试验值接近。

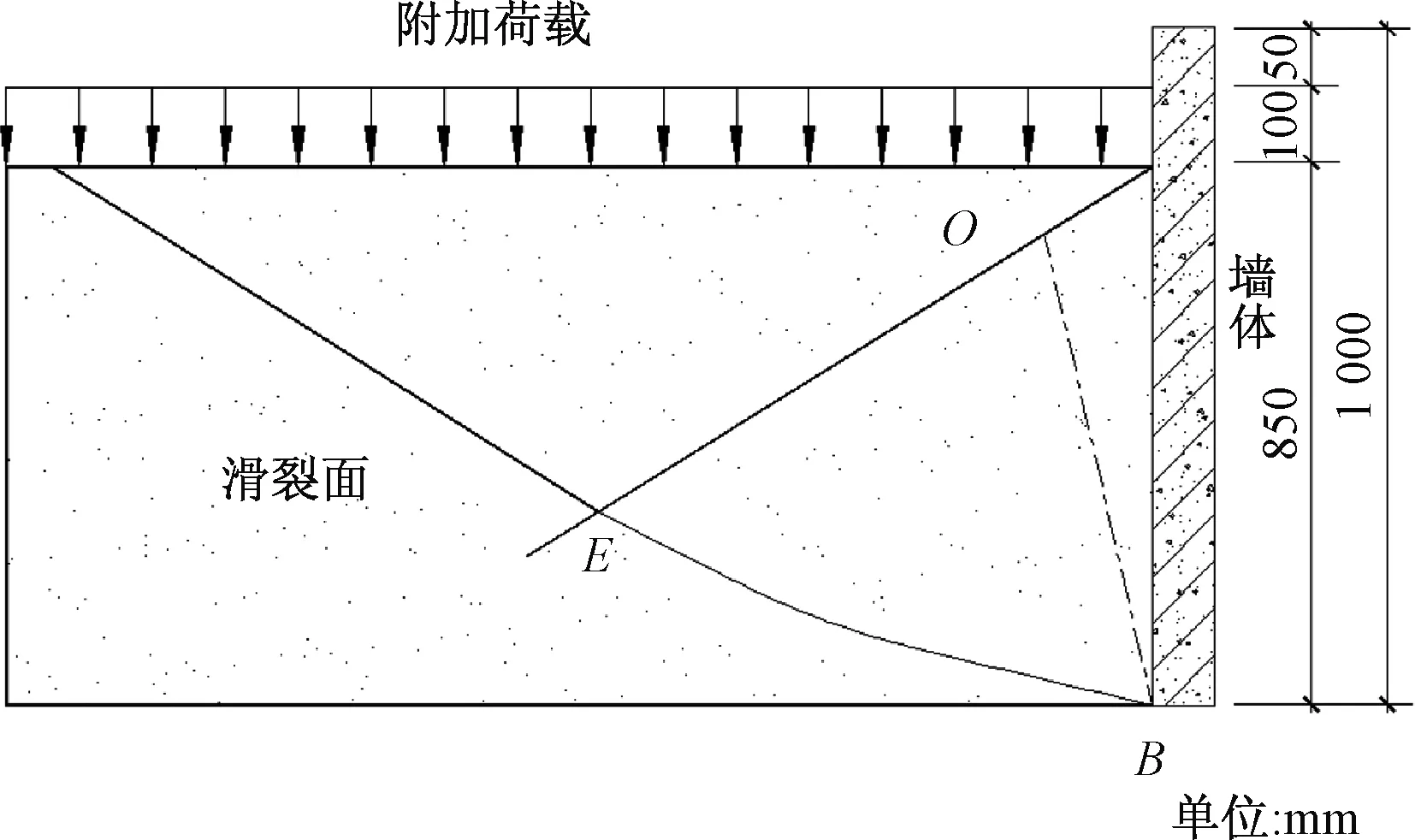
图7 0.1 m厚土层换算成附加荷载示意图Fig.7 Schematic diagram illustrating the conversion of 0.1 m thick soil into the equivalent amount of additional load

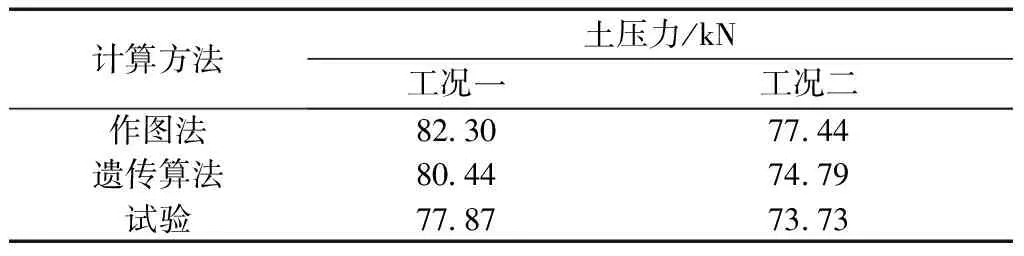
表1 不同方法计算土压力Table 1 Calculation of earth pressure by different methods

4 结论

既有文献采用对数螺旋组合面求解黏土被动土压力时,未考虑到挡墙后填土面上分布有均布荷载的工况,也未考虑到填土面倾斜的工况,基于对数螺旋组合面原理,针对挡墙后填土面上分布有均布荷载的工况,采用作图法将均布荷载加入黏土被动土压力求解过程中,针对墙后填土面倾斜的工况,采用作图法将倾斜填土转化成集中荷载加入到黏土被动土压力求解过程中,同时利用三角函数推导出其被动土压力函数,将其作为目标函数,并基于遗传算法进行求解,并得到如下结论。

(1)遗传算法计算结果与试验值比较,误差为1.4%～3.3%,与试验值接近。

(2)作图法和遗传算法两种方法计算所得结果非常接近,作图法与遗传算法比值为1.023～1.035。

(3)作图法十分烦琐,计算需要耗费大量时间,遗传算法程序简单易用,更利于在工程中应用。研究未考虑土体含水率的影响,可作为下一步研究的重点内容。