秸秆草砖-冷弯薄壁型钢组合墙抗压性能
2021-10-15唐甸葆曹宝珠宋文涛
唐甸葆, 曹宝珠, 宋文涛
(海南大学土木建筑工程学院, 海口 570228)
秸秆作为一种农作物生产过程的剩余产物,用作建筑材料不仅能减缓中国秸秆处理难的问题,同时因其具有低成本、产量大的优点,还能够带来十分良好的经济效应。部分学者[1-3]对秸秆草砖的材料性能进行了研究,发现其拥有保温性能佳、吸声性强、耗能性能好,以及密实草砖不易燃烧等特点,是一种良好的建筑材料。但由于草砖是一种大变形材料,抗压性能相对传统材料较差,因此一般用于低层建筑中,而冷弯薄壁型钢具有自重轻、经济环保、强度高等优点,将秸秆草砖和冷弯薄壁型钢组合起来制成墙体,能够充分加强墙体的抗压能力,具有十分可观的经济前景。
目前,已有学者对秸秆草砖墙体进行了试验研究,陈继浩等[4]对秸秆复合板墙体进行了耐火性能研究,结果表明秸秆复合板墙具有良好的耐火性能;栗剑[5]对不同构造的秸秆草砖墙体进行了对比分析,指出设置有钢丝网或木拉条的墙体比无构造措施的墙体的抗剪刚度有明显提高;袁斌[6]指出采用钢丝网和木龙骨的水泥抹灰草砖墙体其竖向承载力高于未采用构造措施的水泥抹灰墙体,且钢丝网对墙体的影响较大;此外,张秀华等[7]对冷弯薄壁方钢管-稻草板组合墙体的轴压性能进行了试验研究,试验表明稻草板能够提高钢龙骨架的承载能力。Cornaro等[8]对草砖墙以及传统墙体生产建造使用三个环节所需的能耗以及产生的二氧化碳进行统计,指出草砖墙相比传统墙体拥有更低的能耗以及更少的二氧化碳排放;Douzane等[9]对一栋使用石膏草砖墙作为墙体的房屋进行了湿热性能分析,发现墙内温度一年四季较为稳定,不随季节的变化以及昼夜温差的变化而出现大幅度的波动,同时墙内相对湿度相比室外更低、变化幅度更小。
然而,关于秸秆草砖与冷弯薄壁型钢的组合墙体研究较少。为此,设计并制作一种由轻钢龙骨骨架为主要承载构件的秸秆草砖-冷弯薄壁型钢组合墙,并对其进行了抗压性能试验,以此观察秸秆草砖-冷弯薄壁型钢组合墙的破坏形态和破坏的过程,同时还考察了现有的冷弯薄壁型钢规范对组合墙体抗压承载力的适用性,并提出合理的墙体抗压承载力的计算方法。
1 试验概况
1.1 试件设计与制作
试件采用足尺比例设计,试验墙厚500 mm、墙长2 490 mm、墙高2 930 mm,墙体内部骨架由两部分组成,一部分是钢骨架为主要承重构件,其由2片U形钢作为顶、底导梁以及7片C形钢作为立柱以及2片刚拉带作为斜撑组合而成,另一部分是用于固定秸秆砖的非承重木龙骨,由2条横木龙骨以及7条竖木龙骨组成,钢骨架和木龙骨均利用自攻螺钉进行组装同时利用木拉条和自攻螺钉将两者进行连接,墙体内部填充物为经草砖机压制的秸秆草砖,填充完毕后在墙体上铺上一层钢丝网,并在钢丝网上人工涂抹厚度为15 mm的水泥砂浆,试件制作过程详见图1,墙体组件尺寸详见表1,图2为首根钢柱的部分横截面图。

图1 墙体试件制作过程Fig.1 Wall specimen production process
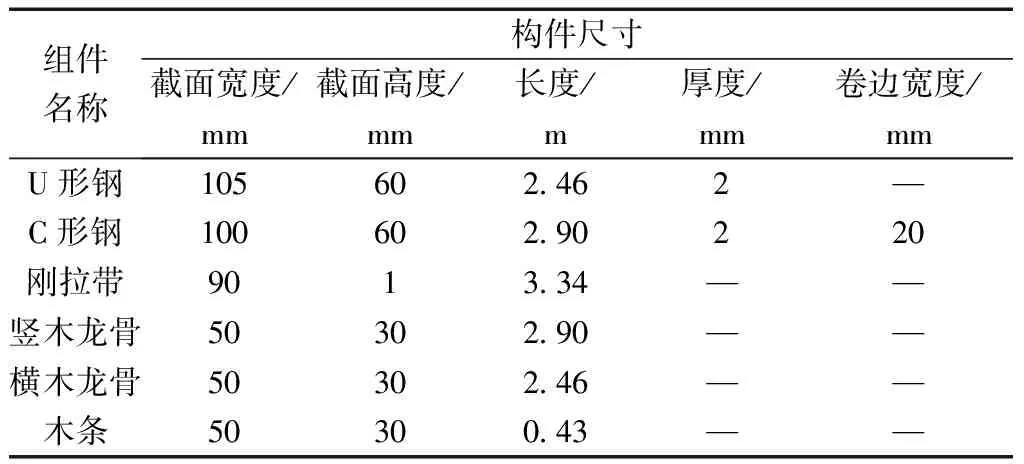
表1 墙体组件尺寸表Table 1 Size table of wall components
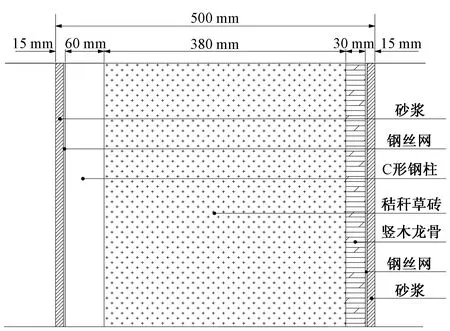
图2 首根钢柱的部分横截面图Fig.2 A partial cross section of the first steel column
1.2 试验材料力学性能
1.2.1 钢材力学性能
试验墙中的钢骨架所采用的C、U形钢均为Q235冷弯薄壁型镀锌钢,刚拉带均为Q345冷弯薄壁型镀锌钢,钢材材料试验是根据《金属材料室温拉伸试验方法》(GB/T 228.1—2010)[10]与《金属材料弹性模量和泊松比试验方法》GB/T 22315—2008)[11],将与试验同一批次的冷弯薄壁型钢以及刚拉带分别截取3块板状试件进行拉伸试验,材料试验结果详见表2和表3。
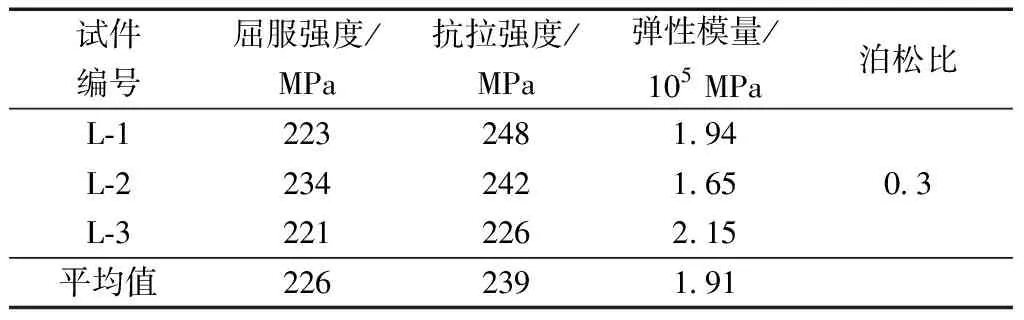
表2 冷弯薄壁型镀锌钢力学性能试验结果Table 2 Test results of mechanical properties of cold-formed galvanized steel

表3 钢拉带力学性能试验结果Table 3 Test results of mechanical properties of steel tension strap
1.2.2 秸秆草砖抗压性能
试验中所用的秸秆草砖原材料来源于海南水稻秸秆,水稻秸秆在制成草砖之前,进行了杂草处理,并对草砖进行了含水率测试,试验所采用的草砖是由草砖机将与秸秆压密成型,最后再用钢丝绑扎固定而成。草砖性能试验所采用的秸秆与试验墙所采用的秸秆为同一批次,所有草砖试件尺寸为400 mm×400 mm×400 mm的立方体,草砖试件详见图3。

图3 水稻秸秆草砖试样Fig.3 The rice straw bale specimens
由于草砖为大变形材料,因此其抗压试验以竖向位移作为草砖的破坏失效条件,当竖向位移为草砖初始高度的1/3时,认为草砖被破坏。试验随机选取三块秸秆草砖,利用万能试验机对草砖进行轴压试验,试验结果如表4所示,草砖应力应变曲线如图4所示。
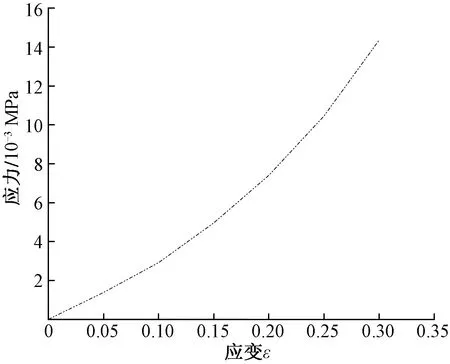
图4 草砖应力应变曲线Fig.4 Stress-strain curve of straw brick

表4 秸秆草砖材性试验结果Table 4 Test results of straw straw brick properties
1.2.3 墙体砂浆强度试验
根据《建筑砂浆基本性能试验方法》(JGJ/T 70—2009)[12],将试验砂浆制成两组共六块的立方体试件,并在与试验墙相同的养护条件下养护28 d后进行强度试验,得出砂浆的平均抗压强度为7.6 MPa。
1.3 试验加载装置
试验利用钢框架以及液压千斤顶来对试验墙体进行加载,钢框架两侧的柱脚通过高强螺栓与地面导槽固定,钢框架上的钢工字梁通过高强螺栓在框架两侧的螺孔上进行固定。试验时先将钢框架上的钢工字梁卸除,再放置试验墙,并在墙顶安放一片分配梁,最后在导梁顶部预留放置液压千斤顶的高度处再安置一片分配梁后再将钢工字梁放回,同时由于墙体没有固定在任何平台上,为避免在试验过程中出现试验墙失稳的情况,试验中还利用铁链将试验墙体、分配梁、千斤顶、荷载传感器固定在钢框架上,试验加载装置详如图5所示。
本次试验利用100 t分离式液压手动千斤顶对分配梁施加荷载,以此实现墙体的均匀加载,试验过程中所施加的竖向荷载的数值大小的采集是通过利用DH-3816静态采集系统将BHR-100荷载传感器中的数据转换而得。
1.4 测点布置及加载制度
为获得试验墙在加载过程中的各部分的变形值,分别在试验墙顶两端各布置1个测点、在试验墙沿高度方向的顶部及中点各布置2个测点、在两个垂直于试验墙长度方向的平面中心点上各布置一个测点,同时在每根钢柱的0.10、1.45、2.80 m处的腹板及外翼缘位置布置共6个应变片,墙体测点以及钢柱应变片布置如图6所示。试验的加载方式为单调多级加载,在正式加载前先进行预加载至50 kN并保载10 min后卸载再进行试验,试验开始时,每级荷载增量为5 kN并保持加载3 min,当试验墙出现裂缝时,每级荷载增量降至3 kN,当墙体竖向位移增加而荷载不断下降或者墙体有明显的破坏特征时,认为试验墙达到极限承载能力,终止试验。

图6 测量点以及应变片布置Fig.6 Measurement points and strain gage arrangemen
1.5 试验破坏特征
试验墙体加载初期,墙体近钢架侧墙面顶、底部的砂浆先出现裂缝,紧接着两侧墙面顶、底部也开始出现微小裂缝,随着荷载的增加,墙体近钢架侧墙面顶、底部靠边缘的砂浆开始出现脱落的迹象,同时两侧墙面裂缝随着荷载的增大而扩展,当荷载继续增大时,墙面底部的砂浆出现粗且宽大的裂缝,墙面顶部的砂浆被压碎而脱落,两侧墙面裂缝最终伴随着轻微响声贯穿墙面形成一条斜裂缝,在试验加载后期,墙体近钢架侧墙面中间出现自下而上的细小裂缝,墙面底部砂浆基本被压碎,顶部砂浆脱落严重,墙体两侧墙面底部出现多处裂缝并开始出现鼓包,当荷载快接近583 kN时,墙体两侧墙面底部裂缝变宽且鼓包现象十分明显,墙体竖向位移不断增加,荷载开始出现下降趋势,但此时试验的加载过程开始出现大且沉闷的响声,考虑试验加载的荷载接近钢框架反力架的加载极限且破坏现象明显,为保证试验人员的安全,认为试验墙体达到其正常使用极限承载力并终止试验。组合墙体破坏现象如图7所示。

图7 墙体破坏现象Fig.7 Wall failure phenomenon
2 试验结果及分析
2.1 试验墙体的荷载-位移曲线
图8为试验墙体的竖向荷载位移曲线,从图8中可知,当墙体竖向位移小于8 mm时,位移与荷载基本上呈正线性关系,但当施加的荷载接近583 kN时,荷载开始趋于稳定并有下降趋势,墙体竖向位移仍在不断的增加,此时试验墙体达到其极限承载力。

图8 墙体荷载位移曲线Fig.8 Wall load displacement curve
试验墙体的荷载平面外位移曲线如图9所示,由图9中可知当荷载小于358 kN时,近钢骨架和近木骨架两侧墙面位移变化较小,荷载接近387 kN时,两侧墙面位移迅速增大,当墙体平面外位移达到5.3 mm时,近木龙骨侧墙面平面外位移值与近钢骨架侧墙面平面外位移值出现明显分岔点,近钢骨架侧墙面平面外位移值仍随着荷载的增加而增大,而近木龙骨侧墙面平面外位移值则停止变化直至荷载达到试验墙体的极限承载力。

图9 墙体荷载平面外位移曲线Fig.9 Outward displacement curve of wall load plane
2.2 墙内钢骨架的荷载-应变曲线
试件内钢骨架作为墙体的主要受力构件,钢骨架立柱的应变能反映墙体的受力情况,每根钢柱取其0.10、1.45、2.80 m处腹板处的应变,各钢柱的荷载应变曲线见图10。从图10中可以看出,试验加载初期,钢柱应变变化较小,荷载应变曲线基本为线性,而在加载后期,由于应力达到了钢材的屈服强度,钢柱应变急剧增加,其中钢柱3中1.45 m腹板处的应变突然骤增且超过钢材的屈服应变,为便于观察其荷载应变曲线,图10中并未给出骤增后的值。结合试验现象,钢柱3中1.45 m腹板处的应变突然骤增的原因可能为:由于荷载的增大,砂浆被破坏并退出承载,而砂浆退出承载的力由墙体内部的钢骨架承担,但此时钢柱所承受的荷载会骤增,因此钢柱此刻的应变很可能也会发生突变。同时,从图10中可以看出,当荷载达到墙体极限承载力时,所有钢柱均已发生屈服。
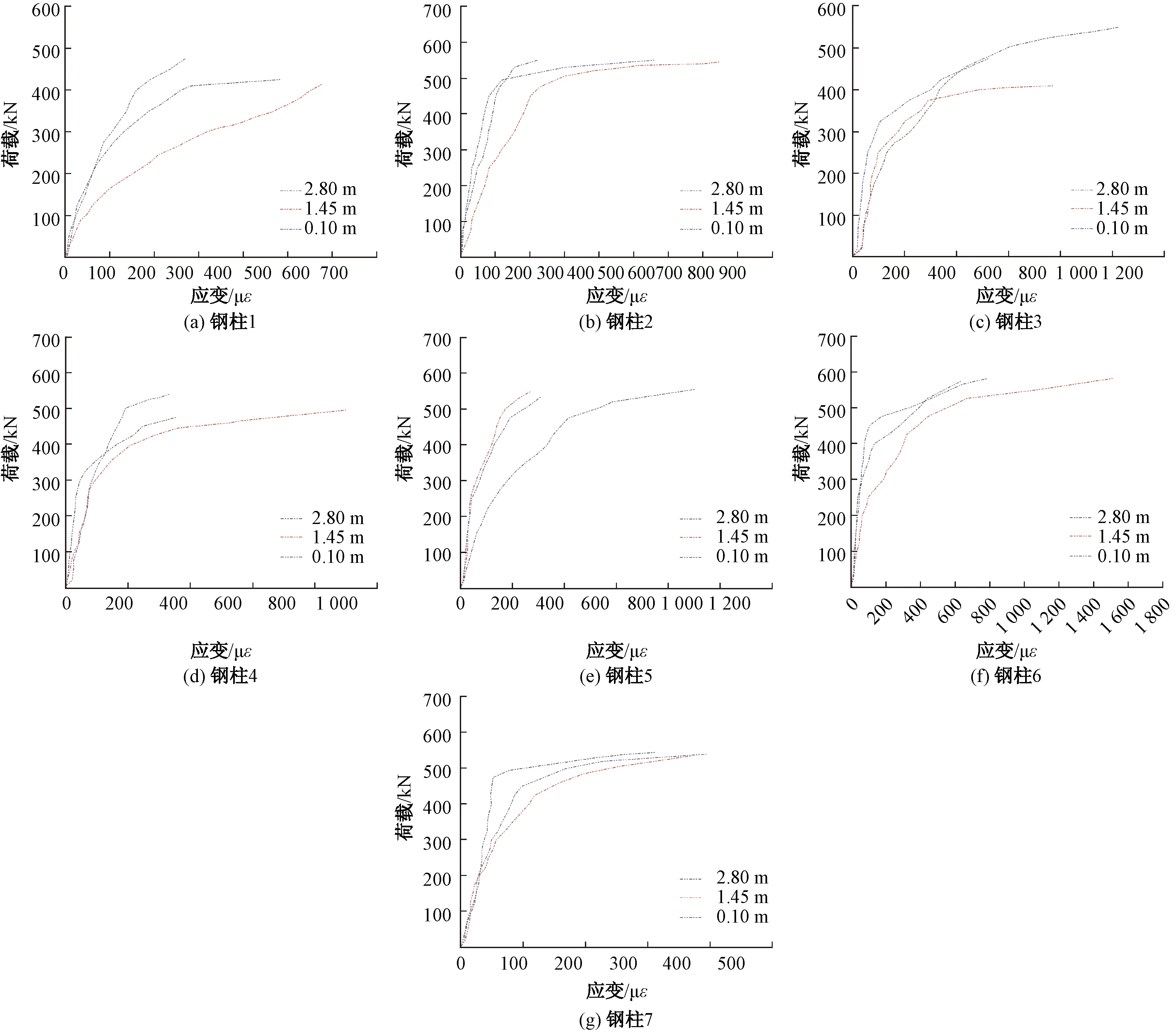
图10 各钢柱的荷载应变曲线Fig.10 Load-strain curve of steel column
3 墙体竖向承载力计算
墙体由压实的秸秆草砖和冷弯薄壁型钢组合而成,虽然草砖提供了一定的承载能力,但是冷弯薄壁型钢仍为主要的承载构件,考虑到这一点,计算墙体承载能力时利用了《冷弯薄壁型钢结构技术规范》(GB 50018—2002)[13]以及北美规范AISI S100—16[14]中的部分计算公式进行了计算。
3.1 中国组合墙体计算方法
试验墙体只承受竖向荷载且为均匀布载,因此认为墙体内部冷弯薄壁型钢柱为轴心受压构件,根据中国规范[12]有
N=φfAe
(1)
式(1)中:N为构件承载力;φ为轴心受压构件的稳定系数;Ae为有效截面面积;f为钢材的抗压强度设计值;由于C形钢为单对称截面,因此其轴心受压稳定系数φ由截面y轴的长细比λy以及弯扭屈曲的换算长细比λω决定,计算方法为
(2)
(3)
(4)
(5)
(6)
lω=βl
(7)
式中:lox、loy分别为构件在垂直于截面主轴x轴和y轴的平面内的计算长度,这里取墙柱实际长度2 900 mm;ix、iy分别为构件毛截面对其主轴x轴和y轴的回转半径;Iω为构件毛截面扇性惯性矩;It为构件毛截面抗扭惯性矩;e0为毛截面在对称轴上的弯心坐标;α、β为约束系数,钢柱两端铰接,端部自由翘曲,均取1;lω、l分别为扭转屈曲的计算长度和构件的几何长度,这里为实际长度2 900 mm;A为毛截面面积;具体的计算值如表5所示。

表5 墙柱长细比计算Table 5 Wall column slenderness ratio calculation
由计算结果以及规范[13]可知取161.5作为构件长细比,并查表得φ=0.270;此外钢柱有效截面面积需由下列公式进行计算。
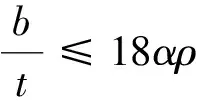
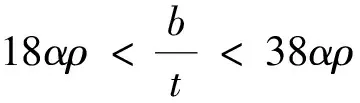
(8)
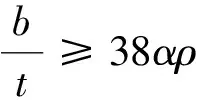
(9)
(10)
式中:b为板件宽度;t为板件厚度;be为板件有效宽度;α为计算系数,因构件均匀受压且只承受竖向荷载这里均取1;bc为板件受压区宽度;σ1为受压板件边缘的最大应力;ρ为计算系数;k1、k分别为板组约束系数和板件受压稳定系数,其中k1、k计算方法较为复杂,因此不再列出计算公式,具体的计算值见表6。

表6 墙柱板件有效宽度计算Table 6 Calculation of effective width of wall column plate
据式(1)可得单根钢柱的承载能力为30 754 N,而墙体钢柱的承载能力约为215 kN,显然与试验值相差太大,这是因为利用规范计算时,仅考虑了钢柱单独承载的情况,冷弯薄壁型钢柱在单独受轴压荷载时,往往会发生局部或者畸变等屈曲,因此实际承载力会比只考虑受压面积和抗压强度计算出来的承载力要低。
同时由表4以及钢柱承载力的计算值可知草砖本身所提供给墙体的承载力可以忽略不计,墙体承载力要比规范计算值高是因为草砖作为墙体填充物对钢柱有支撑作用,能够防止钢柱部分的屈曲,因而提
高了钢柱的承载力。然而草砖对钢柱承载力的贡献的计算较为复杂,这里将试验墙体看作为单面覆板墙体,根据文献[15]可知,此时可取长度系数0.35,即构件在垂直于截面主轴x轴和y轴的平面内的计算长度为0.35×2 900 mm=1 015 mm,并代入式(1)重新计算可得单根钢柱的承载能力为80 689 N,则墙体钢柱的承载能力约为565 kN,这与试验值583 kN十分接近。
3.2 北美组合墙体计算方法
北美规范对受轴压荷载的墙柱的承载力Pnl计算大致分为两种,一是考虑局部屈曲与整体屈曲相互作用的承载力计算方法,二是考虑畸变屈曲的承载力计算方法,并从两者中选取其中最小值作为构件的承载力,其中第一种方法还可细分成有效宽度法和直接强度法,主要采用有效宽度法进行计算,根据北美规范[14]有
Pnl=AeFn
(11)
式(11)中:Ae为有效截面面积,经试算试验墙体C形钢柱全截面有效,因Ae的计算公式较为繁杂,在此不列出其计算过程;Fn为名义压缩应力计算公式为
(12)
式(12)中:Fy为钢材的屈服强度;λc为构件名义长细比,其计算公式为
(13)
式(13)中:Fcre为整体弹性临界应力,其值计算公式为
(14)
式(14)中:β为计算系数;σex为构件在主轴x轴上的屈曲应力;σt为构件的扭转屈曲应力;具体的计算值见表7。由结果结合式(11)可知单根钢柱的承载能力为15 730 N,即墙体承载力为110 kN。

表7 北美规范下墙柱承载力计算Table 7 Calculation of bearing capacity of wall column under North American code
3.3 计算结果对比分析
各种不同计算方法墙体承载力的计算值与试验值如图11所示,为了能够更直观地对比试验值与计算值,表8给出了各种计算方法下试验值与计算值的比值(简称“试算比”)。
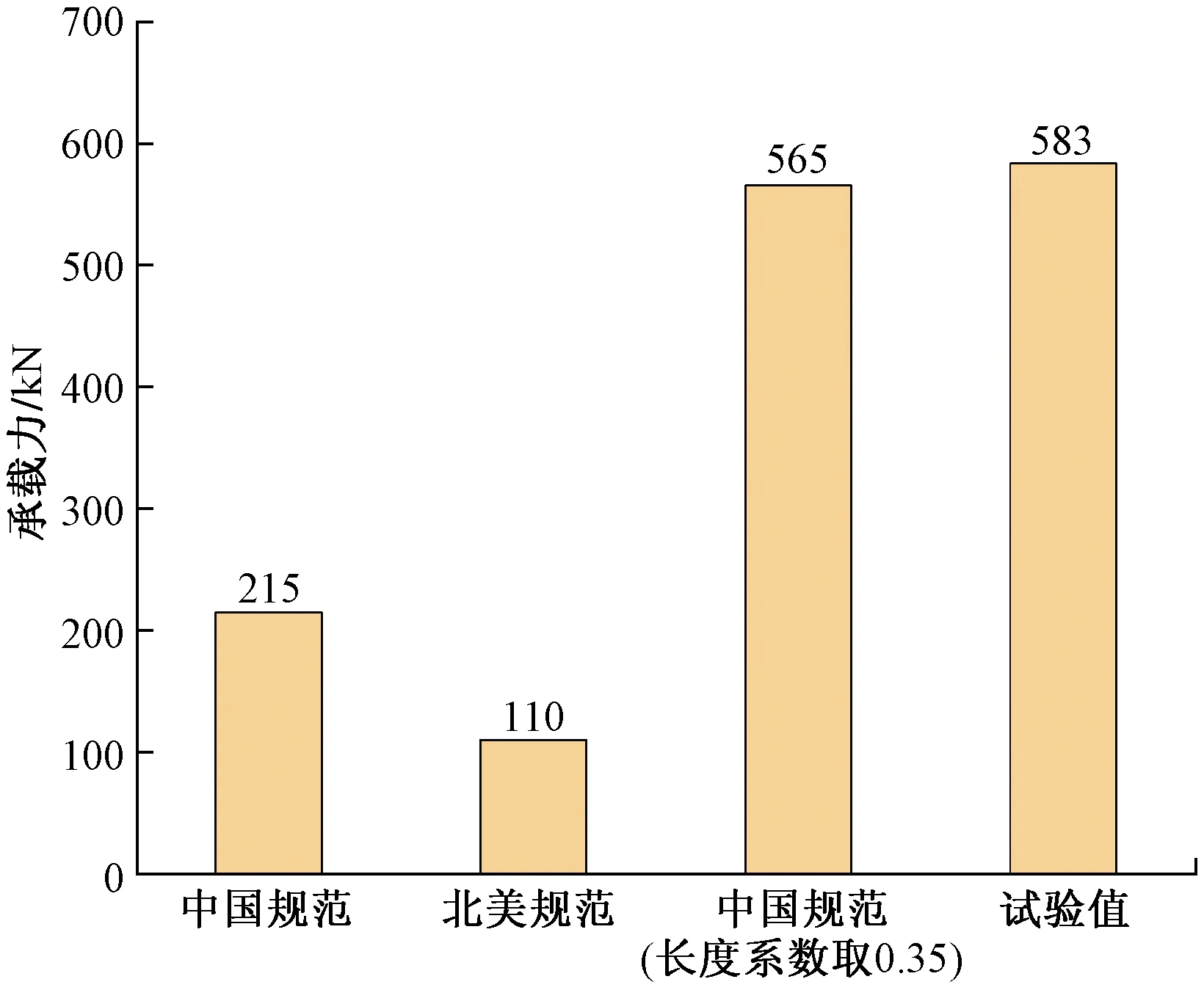
图11 墙体承载力的计算值和试验值Fig.11 Calculated and tested values of bearing capacity
由表8可知,当考虑草砖对钢柱的支撑作用时,即当长度系数取0.35时,此时利用中国规范计算出来的承载力更接近本文组合墙体的实际承载力,而不考虑草砖的对钢柱的支撑作用而直接单独计算钢柱的承载力比试验值要低,可见草砖作为墙体内部填充物对钢柱的承载力有非常明显的提高。

表8 不同计算方法下的试算比Table 8 Ratio of the experimental value to the calculated value under different calculation methods
4 结论
(1)当达到组合墙体极限承载力时,墙体破坏形态为表面砂浆部分脱落且顶底端砂浆被压碎,墙体短边两侧底部出现鼓包现象以及顶部出现长而粗的斜裂缝,此外墙体内部钢柱均已屈服,近钢骨架侧墙面平面外位移大于近木龙骨侧墙面平面外位移。
(2)由草砖的材性试验以及钢柱的计算值和组合墙体承载力试验值表明,草砖基本不为墙体提供直接的承载力,但作为墙体内部的填充物对钢柱的承载力有着十分明显的提高。
(3)采用中国规范对墙体进行承载力计算时,若不考虑草砖对钢柱的支撑作用计算出来的墙体承载力偏于安全,而考虑草砖对钢柱的支撑作用即长度系数取0.35更符合组合墙体实际的极限承载力,若采用北美规范计算墙体承载力则墙体承载力偏小。
