基于SIMS的车辆主动悬架控制研究

李力

（湖南工业职业技术学院，湖南 长沙 410000）

1 引言

主动悬架因其具有良好的隔振减震和抑制车辆振动的性能而受到广泛的关注，不同于传统的被动悬架，主动悬架运用了先进的传感测量技术、计算机控制技术以及机械动力学等。主动悬架由信息传感单元、计算机控制单元和执行机构单元组成，其中，信息传感单元和计算机控制单元是当前主动悬架技术的研究重点[1,2]。

2 捷联式惯性测量技术

惯性技术基于牛顿运动定律，能较精确地测量运动物体各种状态数据，是一种较为理想的获取运动物体姿态、速度等数据手段。SIMS（Strapdown Inertial Measurement System）即捷联式惯性测量系统，它将陀螺仪和加速度计等惯性测量单元固定安装在需要测量姿态、航向、速度等参数的运动载体上，计算机通过信号处理算法计算得到被测运动物体的状态参数[3,4]。

本文的主动悬架控制技术研究以车身的振动和姿态数据为基础，采用SIMS捷联式惯性测量技术来获取车身的姿态、航向、速度等信息，将SIMS固定安装在车辆质心处，SIMS与车辆刚性连接，因此可以实时采集到车辆的运动及姿态信息。

3 7自由度整车动力学模型

车辆的振动是多自由度的复杂机械运动，本文的研究对象是车辆主动悬架的控制，因此需建立整车的动力学模型。本文涉及的车辆7个自由度分别为：车身侧倾运动、车身垂向振动、车身俯仰运动以及4个簧下质量的垂向运动[5,6]，主动悬架采用并联结构形式，即在被动悬架上并联一个主动液压缸，根据电液主动悬架结构得到车辆整车的7自由度主动悬架数学模型[1]，如图1所示。

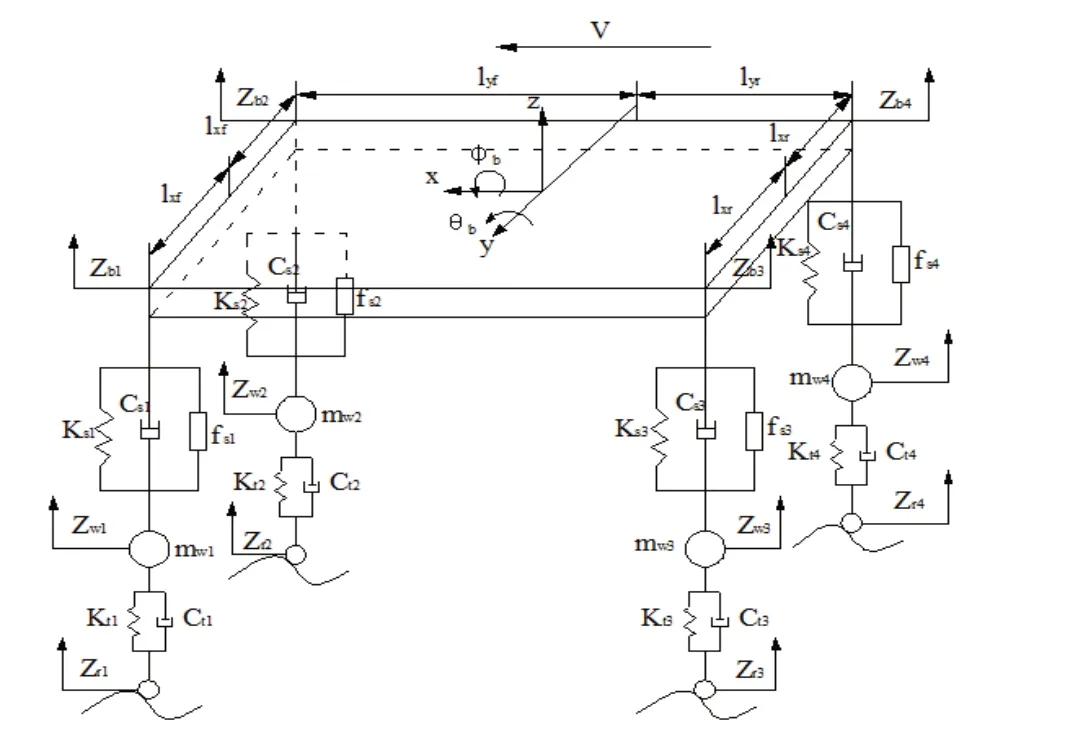
图1 7自由度主动悬架模型

本文在进行动力学分析时，设定车辆沿直线匀速行驶，由动力学原理可推得车辆的动力学矩阵方程为：

式中，[C]为阻尼矩阵，[K]为刚度矩阵，F(t)=[f1,f2,f3,f4]。

将上式展开，即可得到车辆车身质心的垂向运动方程：

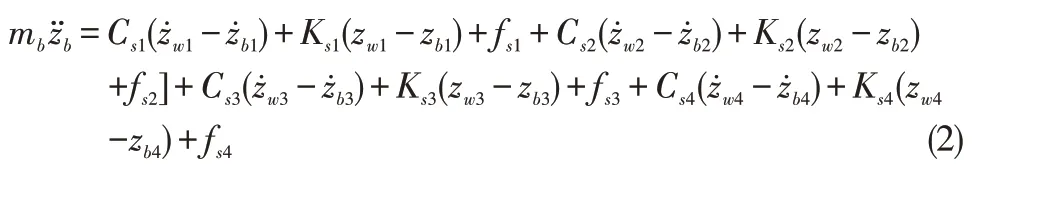
可推得车辆车身的俯仰运动方程为：

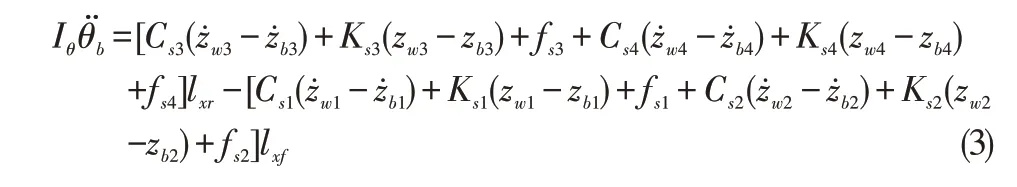
同理，车辆车体的侧倾运动方程为：

若车身的俯仰角θb和侧倾角ϕb的振动幅度都限定在较小区间内，根据刚体运动理论，由车身俯仰角θb、车身侧倾角ϕb、车身垂向位移zb即可得到簧上质量4个端点处在垂直方向上的位移，表达式分别为：

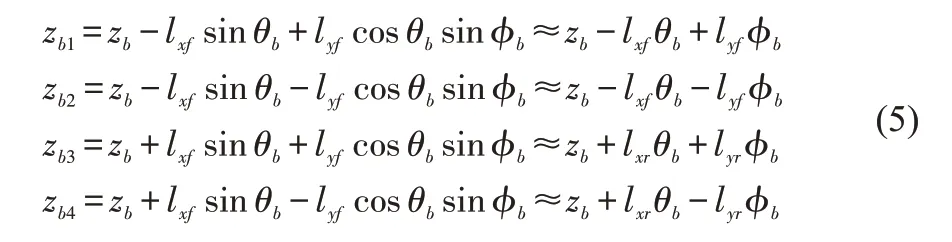
上述动力学推导中，车身侧倾角ϕb、车身俯仰角θb、车身质心垂向位移zb均为可由SIMS测量获取的已知量，在此基础上即可进一步对主动悬架的控制策略进行研究。

4 整车主动悬架分散控制策略

本文选取车身俯仰角θb、车身质心垂向位移zb和车身侧倾角ϕb作为控制指标，采用大系统分散控制理论，将整车的车身垂向、车体俯仰及侧倾振动控制指标分散到4个1/4车体的控制，从而将主动悬架的整车控制转换成4个子控制系统[1]。

4.1 整车姿态的分散变换

上文动力学推导中已得到zb1、zb2、zb3、zb4与zb、θb、ϕb之间的变换关系，将该式改写矩阵形式：

其中，zbx=[zb1zb2zb3zb4]T；zB=[zbθbϕb]；

主动悬架控制的目标是当车辆在行驶过程中因路面输入的干扰而产生车身姿态偏移时，通过主动机构的调控使车身的垂向位移zb、侧倾角θb、俯仰角ϕb快速收敛至平衡稳定状态，令平衡状态时：

垂向位移zb、侧倾角θb、俯仰角ϕb的误差可表示为：

利用式（6）的转换变换矩阵T可将整车的垂向位移zb、侧倾角θb、俯仰角ϕb误差ez、eϕ、eθ分散转换为车身的垂向误差：

其中，e=[eb1eb2eb3eb4]T，T为转换变换矩阵；es=[ez eθeϕ]。

对式（6）进行两次求导：

依据上述推导过程同样可得出：

其中，eb¨x=[eb¨1eb¨2eb¨3eb¨4]T，T为转换变换矩阵；es¨=[ez¨eθ¨eϕ¨]。

经过上述分散变换，整车的姿态zb、θb、ϕb和加速度z¨b、以及误差ez、eϕ、eθ被转换为车身的垂向的位移zb1、zb2、zb3、zb4和加速度以及位移误差eb1、eb2、eb3、eb4，整车姿态控制变换为分别对4个车身的控制。

4.2 模糊自整定PID控制

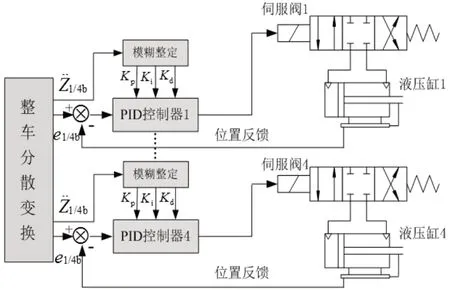
图2 子系统模糊自整定PID控制器结构原理图

如图2所示，通过整车姿态的分散变换后，整车的主动悬架控制也转换成对4个车身的控制，具体的控制采用增量式PID控制算法，表达式如下：

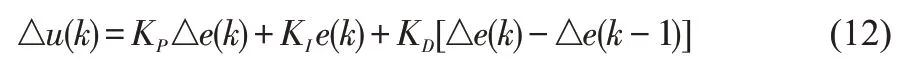
其中，△e(k)=e(k)-e(k-1)。

同时，为了避免主动悬架的主动控制液压缸过于频繁的动作，防止因此带来的车身高频振荡，本文在PID控制器中加入了控制死区，表达式如下：

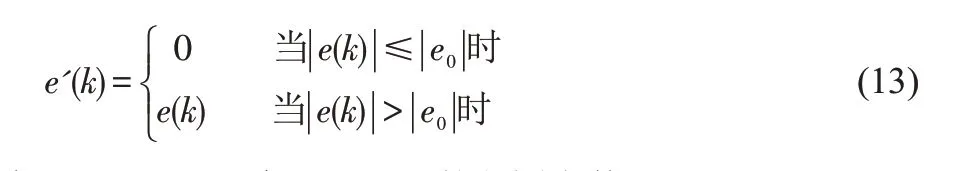
式中，死区e0是一个可以调节的范围参数。

KP、KI和KD三个参数的整定是PID控制算法中及其重要的一环，由于悬架系统存在非线性和时变性，传统的PID参数整定不适用于主动悬架的控制，为此，本文采用模糊参数在线自校正技术对KP、KI和KD三个参数进行在线校正，控制器的控制指标为eb1、eb2、eb3、eb4和z¨b1、z¨b2、z¨b3、z¨b4，目标抑制车身姿态变化并使之快速回到平稳状态。

根据二维模糊参数自整定原理，根据悬架工作特性设计出模糊推理规则：

（1）当ebx(x=1,2,3,4)比较大时，车身垂向偏移较大，此时需液压缸输出较大的控制力来抑制车身振动幅度，KP系数适当取大，同时，为了避免微分饱和，KD系数取较小的值，为了防止超调和积分饱和，KI系数取小值，直至切除掉积分环节。

（2）当ebx(x=1,2,3,4)比较小时，此时控制器的主要任务是消除静态偏差、避免超调和振荡，因此，KI系数要增大，KP系数要减小。

（3）当ebx和z¨bx同向时，分两种情况：一种是 ||ebx较小而较大，此时车身处于振动的初始阶段，趋势强但行程小；另一种情况是 ||ebx较大而 ||z¨bx较小，此时车身振动处于峰值，行程大但趋势弱；同理可推得ebx和z¨bx反向时车身的振动规律，以此规律为依据即可对KP、KI和KD三个参数进行在线修正。

根据上述悬架控制规律即可得到PID参数模糊整定规则表，进而完成PID参数的整定。

5 仿真实验与分析

本文对主动悬架系统的控制进行了仿真验证，仿真基于AMESim与Simulink的联合仿真平台[8]，以天马牌越野车为研究对象，仿真过程中的车辆参数遵循该越野车真实数据。

5.1 阶跃路面输入

阶跃输入是对控制系统的严峻考验，本文首先以阶跃路面为输入对设计的主动悬架控制策略进行仿真分析，设置仿真时间为10s，仿真步长为0.001s，车速为20m/s，阶跃路面产生20cm的垂向阶跃，如图3所示。在该阶跃路面输入至车辆左前轮，进过计算机仿真运算，得到同参数同工况下整车主动悬架和被动悬架的车身俯仰、侧倾和垂向振动曲线，如图4～6所示。

图3 阶跃路面输入

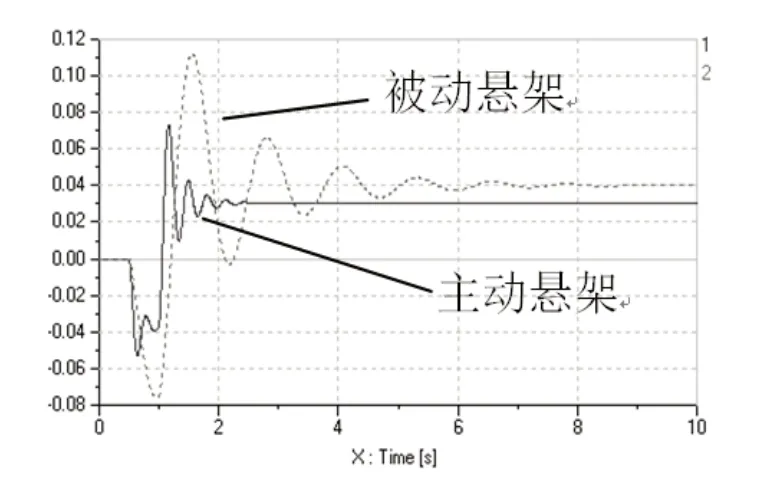
图4 阶跃路面车身俯仰振动

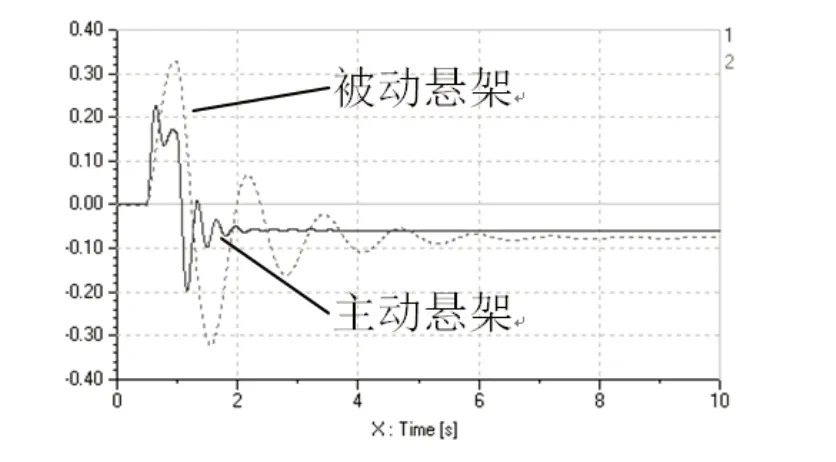
图5 阶跃路面车身侧倾振动

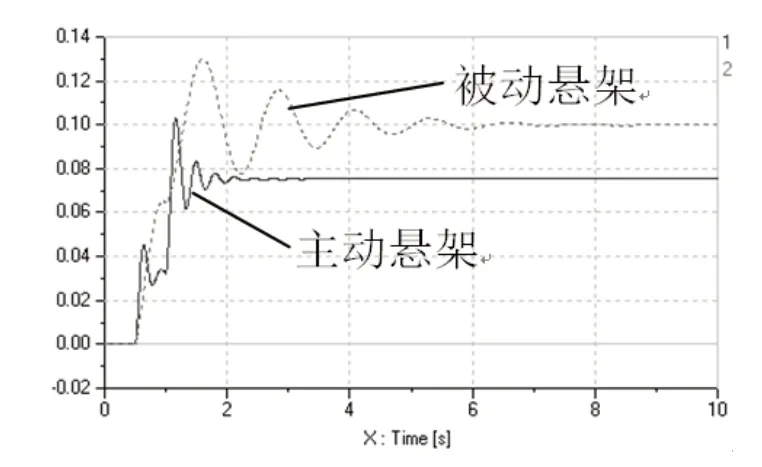
图6 阶跃路面车身垂向振动

对比车身的俯仰、侧倾和垂向振动曲线，在同参数同工况阶跃路面输入的情况下，相较于被动悬架，主动悬架在车身的俯仰、侧倾和垂向的振动都能快速收敛并达到稳定状态。

5.2 包块路面输入

包块路面也是在悬架研究时常采用的路面输入，本文采用一个高度为10cm的光滑凸起状包块为路面输入，仿真时间设置为10s，步长0.001s，车速20m/s，包块路面如图7所示。将该包块路面输入至车辆左前轮，经过计算机仿真计算，得到车身的同参数同工况下整车主动悬架和被动悬架的车身俯仰、侧倾和垂向振动曲线。

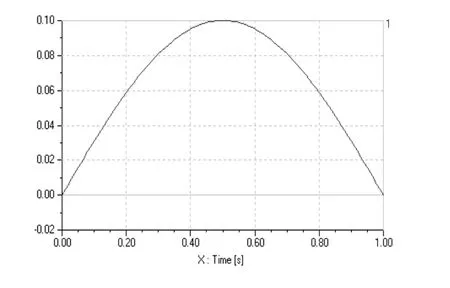
图7 包块路面输入

图9 包块路面车身侧倾振动

图8～图10所示的曲线可以看出，在相同包块路面冲击下，主动悬架的车身垂向振动、俯仰振动以及侧倾振动的幅值小于被动悬架，振动的收敛速度快于被动悬架，主动悬架在包块路面干扰下控制车身快速地回到了平衡位置，这也说明本文研究的主动悬架控制策略能较好地控制车身抑制因路面干扰引起的振动。

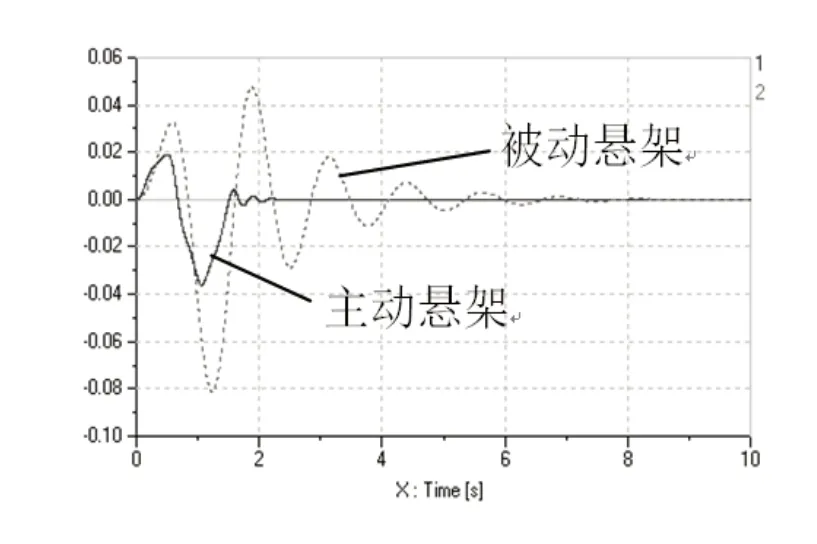
图8 包块路面车身俯仰振动

图10 包块路面车身垂向振动

6 结语

本文对基于SIMS的车辆主动悬架控制技术进行了研究，通过SIMS获取车身姿态信息，对整车主动悬架进行了大系统分散控制，最后采用模糊自整定PID控制器对主动悬架执行机构进行控制，通过计算机仿真分析可得，在阶跃路面、包括路面干扰输入下，相较于传统的被动悬架，本文提出的基于SIMS的车辆主动悬架控制方案能较好地抑制车辆行驶过程中因路面干扰引起的车身垂直跳动、俯仰以及侧倾运动，能快速对车身姿态进行调控使之回到稳定状态。