Verhulst模型在滑坡预测预报中的应用研究

黄精涛 李金轩

(东华理工大学 水资源与环境工程学院，南昌 330013)

滑坡预测预报的研究和应用，一直都是灾害研究领域的重点[1]，也是国内外研究的热点，对滑坡开展合理有效的预测预报也是一直困扰着诸多专家学者的一大难题。经过国内外专家学者多年的精心研究，在滑坡的预测预报方面取得了不错的成效，滑坡空间的预测预报从早期的灾害前兆预报、安全系数法到现今的多方法综合预报预测，时间的预测预报从斋藤迪孝模型的引入到现在的5G技术的综合应用等，都在生产实践中得到充分应用，其模型和方法的改革创新也步入了新时代。

在滑坡的预测预报研究中，常见的预测预报模型和方法有斋藤模型、福囿(Fukuzono)模型、苏爱军模型、Verhulst模型、BP神经网络法、灰色(G，M)理论、信息模型法、灾变模型预测法、模糊综合评判法、线性回归模型法、聚类分析模型法、多因子定量分析模型法、非线性动力学模型预测法、多参数预报法、黄金分割法及Pearl模型法等。但在诸多的研究方法和模型中，研究应用最多的当属灰色(G，M)理论和Verhulst模型。本文基于Verhulst模型在滑坡预测预报中的研究应用，探讨Verhulst模型的发展改进，以期为该模型的应用以及进一步的优化提供帮助。

1 传统Verhulst模型

1.1 Verhulst模型基本原理

(1)

式中：a、b为待定系数，可通过最小二乘法原理和求极值的方法求解，x表示滑坡滑动的位移量，t表示滑坡滑动时间的预测值，求解方程得：

(2)

式中：x0、t0表示初始位移值和时间，当x=a/2b时，dx/dt出现极大值，即此时的滑坡滑动时间tr为滑坡发生时间的预测值，可由式3求解得到：

(3)

1.2 Verhulst模型在滑坡预测预报中的应用

在Verhulst模型的应用中，诸多学者都基于重大滑坡实例进行了短期预报和临滑预报验证，结果表明Verhulst模型预测效果良好，精度较高。晏同珍最早将Verhulst模型应用到滑坡预测预报中，基于此法对长江新滩滑坡、甘肃黄龙西村滑坡以及意大利Vaiont滑坡数据进行验证研究，其预测检验结果较为成功；殷坤龙等[2]也用Verhulst模型对鸡鸣寺滑坡进行了预报验证，结果显示其精度极高；温文等[3]利用 Verhulst 模型对黄茨滑坡进行时间预测，其预测效果也较好。此外，有不少学者对Verhulst预测模型进行了创新，推出Verhulst预测模型程序化应用。他们使用计算机 VBA 语言对Excel进行二次开发，在一定程度上提高了数据操作和分析的效率。如：曾程[4]、程江涛等[5]以及覃秋雅等[6]基于Verhulst模型，使用Excel内嵌的VBA语言，对1995年甘肃省兰州市的黄茨滑坡进行验证，并且曾程、程江涛等还基于灰色(1，1)模型进行了对比分析，其对比结果证实了Verhulst模型在滑坡预测预报中具有较好的适用性，依托此法对软件的开发改进是可行的。

以往研究中，原始Verhulst模型是以速度达到最大值时刻作为滑坡滑动的预报判据，根据陶干强等[7]的研究，Verhulst预测模型变形位移与速度和时间的关系如图1所示。

图1 Verhulst预测模型位移和速度随时间的变化曲线Fig.1 Curves of displacement and velocity of Verhulst prediction model over time

由图1可以看出，随时间的延长，位移和速度不断增大，当速度达到最大时，并没有出现位移最大值。所以，单纯的由速度变化情况或以速度达到最大值来预测预报滑坡发生的时间是片面的且与客观事实不符合。为此，一大批研究人员对原始Verhulst模型进行了改进和创新。

对从事快递业已有6年的中通快递员李师傅来说，“双11”就是一场拼体力的战斗。从早上8点到网点取货送货，一直要忙到晚上9点多，“高峰期要送大约300个件，是平时是2到3倍。”李师傅说。

2 Verhulst模型的改进

2.1 Verhulst模型的改进

随着Verhulst模型在滑坡预测预报中的广泛应用，专家学者们对滑坡预测预报研究也越发深入，发现传统的Verhulst模型在某些滑坡预测预报中存在误报的现象，进而对原始Verhulst模型进行了改进和创新。戴文战等[8]对Verhulst模型产生误差的原因进行了分析，并对模型的背景值进行重构优化，提出了结构参数的优化算法，进一步提高了Verhulst模型的精度。并且戴文战还将改进后的Verhulst模型与原始Verhulst模型应用到实例中进行对比验证，结果显示改进后的Verhulst模型应用范围和预测精度方面都要优于传统Verhulst模型。陈露[9]首先利用最小二乘原理对模型初值进行优化，其次基于平均相对误差最小准则利用粒子群算法对模型中的参数进行优化，从而达到模型的二次改进。并且，她还建立了传统Verhulst模型和改进后的Verhulst模型对比仿真实验，结果表明改进模型2(初值和背景值优化，并结合粒子群优化算法)的拟合精度最高，改进模型1(初值优化)次之，传统模型误差最大。王利红等[10]对模型进行反推改进，她假定累加序列中每一个值都为已知的初值，并将其带入模型，应用最小二乘法对每一个累加值求残差，并基于残差最小原则确定最优初值从而对模型进行优化改进，但并未对模型进行验证。为此，贺小黑等[11]基于王利红的改进模型(已知条件的改进)进行了实例验证，并进一步对模型进行了改进(预报判据的改进)，将改进后的模型对比应用到滑坡预测预报验证实例中，结果显示改进的Verhulst模型的预报精度明显高于原始Verhulst模型，而且改进模型的预报时间比原始模型的预报时间更早，并且提出了使用加速度最大判据可以起到提前预测预报的作用。LEAU等[12]基于背景值提出一种自适应灰色算法，并将梯形法则和辛普森1/3法则结合，提出了生成序列可调的自适应灰色Verhulst模型，并对模型进行了验证。李志阔[13]基于最小二乘原理对Verhulst模型进行初值优化，并在平均相对误差最小的准则下将模型的参数优化为线性，从而利用优化算法对参数进行优化。邓洪高等[14]基于传统 Verhulst模型预测精度较低的问题，在灰色马尔科夫Verhulst模型的基础上再次进行改进，最终提出了灰色马尔科夫Verhulst动态模型，并结合新滩滑坡数据对模型进行分析验证。结果表明，灰色马尔科夫Verhulst动态模型综合了原始Verhulst模型和灰色马尔科夫Verhulst模型的优点，且预测预报精度远远优于另外两种模型。

2.2 Verhulst模型改进的优越性讨论

尽管许多专家都对Verhulst模型进行了改进，但仅有很少专家将改进后的模型用于滑坡实例验证。戴文战、陈露以及LEAU等虽然对模型进行了验证，但并未应用滑坡实例。本文主要讨论模型对滑坡预测预报的研究，所以在此仅针对应用到滑坡实例中的模型进行优越性讨论。基于贺小黑和邓洪高改进后的Verhulst模型，利用文献[15]中新滩滑坡B3点的监测数据(详见表1)，对两种改进模型进行对比分析，探讨其在滑坡预测预报中的优越性。

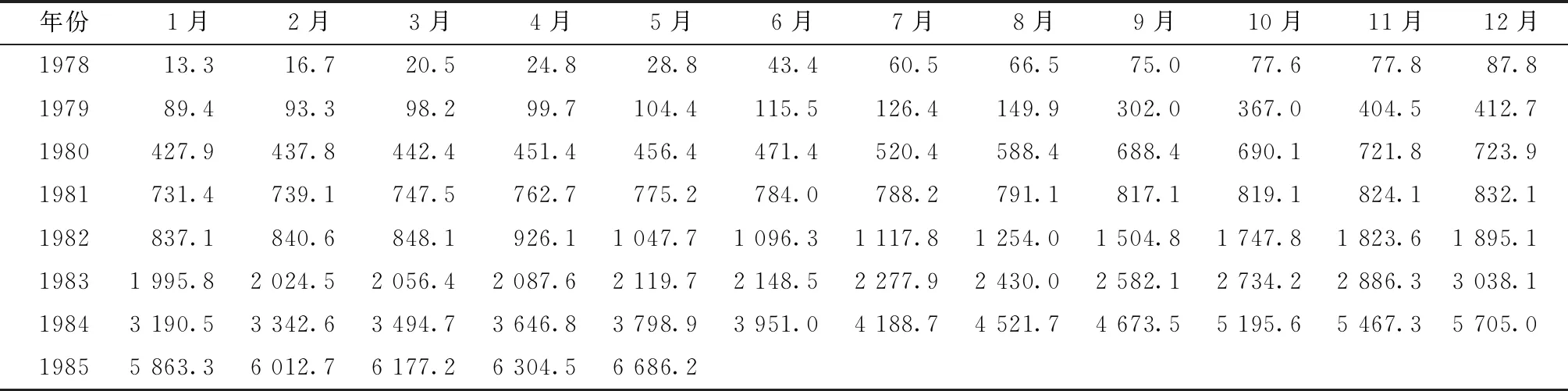
表1 新滩滑坡B3点位移监测值统计Table 1 Displacements of B3 point of Xintan landslide /mm

基于贺小黑和邓洪高改进后的模型，拟合结果如图2所示。从图2可以看出，在滑坡初始阶段(1879年8月以前)，4种模型的拟合值与原始数据比较接近，但随着滑坡位移的增大，灰色马尔科夫Verhulst模型和传统Verhulst模型的拟合值逐渐偏离原始数据且越偏越远；贺小黑改进后的模型首先对数据进行平滑处理，得到的位移时间曲线(简称平滑曲线模型)与原始数据趋势基本保持一致，很好地对滑坡数据进行了预报验证；而邓洪高改进后的灰色马尔科夫Verhulst动态模型拟合值与原始数据发展趋势高度保持一致，数值也十分接近，较好地对滑坡数据进行了预报验证，也是截至目前预测精度最高的模型。

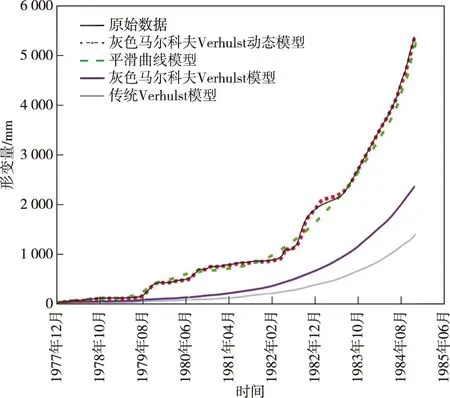
图2 新滩滑坡B3监测点四种模型拟合度对比图Fig.2 Comparison diagram of fitting effects of four models displacements of B3 point of Xintan landslide

3 Verhulst反函数模型

3.1 Verhulst反函数模型基本原理

李天斌等[16]在研究中认为Verhulst模型的预报判据是基于相似性建立的，缺乏理论和量化依据，且Verhulst模型曲线“S”型与边坡变形破坏的典型曲线恰好相反，两者互为反函数(特征曲线见图3)，进而提出了Verhulst反函数模型。其预报模型如下：

图3 Verhulst模型及Verhulst反函数模型特征曲线Fig.3 The character curves of Verhulst model and its inverse function

X(0)(t)={X(0)(1),X(0)(2),X(0)(3)，…，X(0)(n)}

(4)

式中，X(0)(t)为等间隔位移监测数据序列，对其作一次累加并进行生成变换得：

X(1)(t)={X(1)(1),X(1)(2),X(1)(3)，…，X(1)(n)}

(5)

其拟合的Verhulst表达式为：

(6)

求解得：

(7)

对(7)进行反函数求解，并进行变量互换求得Vehrulst反函数模型如下：

(8)

式中，a，b为待定系数，可根据最小二乘法原理求得，t为时间序数。

3.2 Verhulst反函数模型的应用及发展改进

Verhulst反函数模型提出后，逐渐被应用于滑坡的短期预报和临滑预报中。李天斌等[16]提出Verhulst反函数模型后，开展了一系列的实例验证。对三峡库区的某顺层边坡进行了长达4年的监测预报，预报结果比实际提前10天；其次，基于新滩滑坡A3点监测数据，进行为期1年的预报验证，得到的预测结果比实际提前16天；还对黄河龙西滑坡开展预测预报，结果比实际提前8天。徐林生[17]采用Verhulst反函数模型对湖北恩施某公路隧道和新桐公路隧道口围岩变形的突发失稳时间进行预报，结果表明预测精度都较高。龙万学等[18]基于Verhulst反函数模型，选用鸡鸣寺滑坡、加拿大Hogarth滑坡等数据，对滑坡起始预测时刻选择进行深入研究。贺小黑[19]应用Verhulst反函数模型对卧龙寺和黄茨滑坡数据进行预测预报验证。

随着对Verhulst反函数模型的深入研究，Verhulst反函数模型得以不断地创新改进。尹彦波等[20]基于原始的Verhulst反函数模型，建立了地压灾害Verhulst反函数预测模型，并结合了VB编制的计算机模型，对柿竹园多金属矿的地压灾害开展预测预报，结果显示预测结果与工程实际吻合度较高。周中等[21]对Verhulst反函数预测预报模型增加残差项，并应用BP神经网络对残差序列进行二次建模分析，建立了滑坡失稳时间预报的Verhulst反函数残差修正模型预测法。基于此法，对新滩滑坡和加拿大Hogarth滑坡进行预测预报，新滩预测结果比实际边坡失稳时间提前7天，加拿大预测结果与实际破坏时间完全一致。贺小黑[19]通过对原始的Verhulst反函数模型研究，对初始条件理论依据等方面进行改进，提出了非线性拟合的求解方法，并与原始的Verhulst反函数模型进行对比实例验证。在卧龙寺滑坡的验证中，改进后的模型预测结果比实际早2天；在黄茨滑坡的验证中，改进后的模型预测结果比实际早1天，两者都比原始Verhulst反函数模型预测精度更高。

截至目前，Verhulst 反函数模型在滑坡预测预报的研究应用中相对Verhulst 模型较少，且改进创新的Verhulst反函数模型应用研究也相对较少，其预测预报准确性和适用性不明显。

4 结论

1)传统的Verhulst模型和Verhulst反函数模型在国内外的重大滑坡实例中都得到了较好的验证。二者相比较，Verhulst模型在应用验证中，适用性较强，预测精度也较高；而Verhulst反函数模型的预测预报模拟验证中，虽然预测精度高但仅有少数预报是较实际提前的。

2)在Verhulst模型的应用研究中，文章针对原始模型的初值、背景值、判据及运算方法等进行改进研究讨论，总结归纳改进后模型的优越性，高度认为邓洪高等改进的灰色马尔科夫Verhulst动态模型是目前预测精度最为准确的Verhulst模型。而Verhulst 反函数模型在滑坡的应用领域开展的研究较少，相的改进创新的Verhulst反函数模型的应用研究也相对较少，仅在计算方法、初始条件等方面进行了改进，并且在研究中很少对同一滑坡进行验证或者对同一数据的验证切入点不一致，其适用性和预测准确性有待进一步考虑。

3)Verhulst反函数模型相对于Verhulst模型来说，其变形破坏曲线与滑坡的矢量化曲线更接近，并且目前的研究应用较少，在后续的研究应用中Verhulst反函数模型还有很多地方值得挖掘，其较提前的精准预测预报效果还是值得期待的。尽管目前的研究并未很好地证实这一点，但在以后的研究中，可以尝试从初始值、判据、优化运算方法等多方面进行拟合，综合构建模型，并结合人工智能，以期更准确地对滑坡开展预测预报，更好地达到防灾减灾的效果。