如何设计科学、有效、有趣的教育游戏

张露 胡若楠 曾嘉灵 尚俊杰

[摘   要] 近年来，教育技术的发展为创新学习方式带来了前所未有的机遇。针对游戏化学习研究领域的核心问题——如何设计科学、有效、有趣的教育游戏，以学习科学的跨学科为视角设计了数学游戏《分数跑跑跑》。在认知内容设计方面，依据认知神经科学、教育学、心理学等领域的相关研究成果展开设计，为学习者提供科学的认知支持;同时以实践需求作为设计导向，确保游戏使用的有效性。在保障科学性和有效性的基础上，借助游戏元素充分调动学习者情绪动机状态。经检验，《分数跑跑跑》能够显著提高小学四年级学生的分数概念性知识水平。

[关键词] 教育游戏; 游戏化学习; 学习科学; 数学认知; 设计研究

[中图分类号] G434            [文献标志码] A

[作者简介] 张露（1992—），女，黑龙江鹤岗人。讲师，博士，主要从事游戏化学习、数学认知、学习科学与技术设计研究。E-mail：zhanglu1176@163.com。尚俊杰为通讯作者，E-mail：jjshang@pku.edu.cn。

一、引   言

近年来，教师和研究人员逐渐意识到游戏化学习的潜在优势，尝试使用游戏作为教学指导和兴趣激发的工具[1-3]。国内外游戏化学习研究领域高度重视教育游戏的设计与开发[4]，如何设计科学、有效、有趣的教育游戏成为教育游戏研究的关键问题。随着教育领域基础研究的深入、教育技术的不断创新，学习科学这一跨学科领域得以快速发展。学习科学立足教学实践，在探索“人是如何学习的”这一问题的过程中，以跨学科的视角致力于阐释学习的发生机制，分析过程中的学习行为，并借助教育技术进行学习环境的设计。学习科学的研究成果和理论发现也为教育游戏的设计提供了崭新的视角。义务教育阶段的数学教育一直是游戏化学习的重要应用领域。在数学认知研究领域，分数学习在儿童的数学发展过程中具有重要意义，分数学习困难也是普遍存在的现象。信息技术的发展为分数学习创造了更多的可能。随着移动设备的普及和游戏技术的进步，教育游戏支持下的分数学习成为一种趋势，备受教育研究者和实践者的关注。

二、分数游戏的整体设计框架

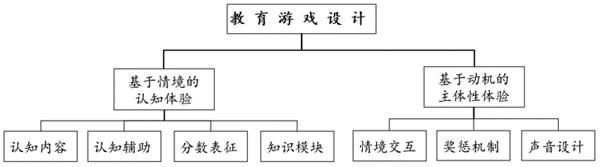
为了实现科学、有效、有趣的游戏设计，游戏化学习的理论框架是产品设计的基础。在游戏设计之前，笔者已通过相关理论要素的推演和归纳，提出了游戏化学习体验的理论框架，归纳了游戏化学习体验的三大范畴，即基于情境的认知体验、基于协作的社会性体验、基于动机的主体性体验。在基于情境的认知体验范畴内，游戏化学习环境可以为学习者提供认知真实性的虚拟学习环境，借助与学习环境的互动与反馈，学习者可以进行知识建构[5]。基于协作的社会性体验主要包含学习者在游戏化学习过程中收获的协作体验和学习指导。基于动机的主体性体验是在社会认知理论的主体性视角（Agentic Perspective）的启发下[6]，主要关注学习者个體的动机、情绪、意愿状态的主体性体验。依据游戏化学习体验框架，本研究在基于情境的认知体验和基于动机的主体性体验两个维度确定了分数游戏的设计体系。

基于情境的认知体验主要涉及分数游戏的教育性认知内容，以实现教育游戏的教育功能为目标。在该范畴内，游戏设计模块包含游戏的核心认知内容、认知辅助工具、表征方式以及难度梯度的设计，内含逻辑线索为“学什么—怎么学—如何呈现—怎样进阶”。基于动机的主体性体验主要涉及游戏化元素为学习者带来的愉悦体验，关注教育游戏的娱乐功能。在该范畴内，游戏设计模块包含游戏情境与交互设计、奖惩机制和声音的设计。游戏的整体设计框架如图1所示。由于教育功能是教育游戏的首要功能，因此，游戏元素的设计服务于认知内容的呈现。

教育游戏在设计之初，需要明确使用目的，这有助于实现教育游戏的有效性。在游戏使用定位方面，本研究的游戏设计旨在辅助教育教学，作为一款注重数学意义建构的练习游戏，将会成为课堂教学之外的补充。

三、认知内容的设计与理论参考

（一）核心认知内容

为理解儿童的分数能力发展，教育学从数学知识发展的角度区分了分数的概念性知识和程序性知识。分数的概念性知识是指对分数符号含义的理解，教育学领域主要聚焦于分数的两大基本含义：“部分与整体”（Part and Whole）以及“测量解释”（Measurement Interpretation）。“部分与整体”是指分数符号呈现了部分与整体的关系，这是理解分数其他含义的基础。儿童在幼儿园阶段已经有了“平分”的生活体验，因此，能够很容易地掌握这部分内容。“测量解释”是指对分数数值大小的理解[7-8]，主要强调数字的表达、比较、排序以及将分数放在数轴对应的点[9]，其中，数轴在建构分数的数值知识方面有广泛的应用[10]。在心理学研究领域，分数通常被界定为一组相互关联的子含义，包括“部分与整体”“比”“算子”“商”“测量”[11-12]。学生需要非常熟悉分数的表征含义，才能对有理数进行有效认知。

作为神经科学和认知心理学的交叉学科，认知神经科学是学习科学研究的重要领域[13]，促进了人类对脑学习机制的探索研究。为研究人脑如何认知分数，Jacob和Nieder通过功能磁共振成像技术开展了针对分数表征的适应性实验（Adaptation Experiment），这项研究表明，符号比率是以抽象的数值概念在人脑中进行表征[14]。同时，教育学领域的相关研究也发现，分数数值表达的准确性与分数计算和数学成就密切相关[15]，理解分数数值含义的学生能够更好地记忆分数的计算步骤[16]。卡耐基梅隆大学分数学习研究中心的Siegler教授曾提出数字发展的整合理论。该理论认为，数学发展是数字认知范围不断扩大的过程，分数在此过程中居于核心地位，而对数值的理解是链接各类数字知识的基础[17]。

以学习科学的跨学科为视角，基于教育学、心理学、认知神经科学领域对分数数值理解知识的强调，结合笔者在前期调研中所发现的四年级学生在“测量解释”知识方面较差的成绩表现，本研究确定以分数概念性知识中的“测量解释”知识作为游戏的核心目标教学内容，以加深儿童分数概念性知识理解的深度。

（二）核心认知辅助工具

在确定数学游戏的核心认知内容之后，还需进一步设计游戏中的教学支架，即核心认知辅助工具的设计。依据分数概念性知识的相关理论，“测量解释”的核心是理解分数在数轴上的数值含义。这与认知心理学家发现的心理数轴（Mental Number Line，MNL）认知模型相吻合。心理数轴是为学习初等算数知识提供的认知模型，儿童需要意识到阿拉伯数字和数词从左到右依次增长，每一个数字都比前一个数字多一个数量。此外，在认知神经科学领域，Ischebeck等人采用功能磁共振成像方法探究了距离效应与大脑顶内沟激活的关系，发现数字的整体距离与右侧顶内沟和枕中回（Middle Occipital Gyrus）的激活水平呈显著负相关，只有整体距离能够调节顶内沟的激活[18]，这进一步支持了数轴对于分数数值理解的重要性。

参考分数认知理论关于数轴的相关研究，本研究确定以数轴作为分数游戏的核心认知辅助工具。与此同时，参考具身认知理论设计认知辅助工具的交互方式。20世纪80年代以来，“具身”得到了认知神经科学、心理学等诸多领域学科的关注，对于人脑“镜像神经元”的发现也为具身认知提供了重要依据。虽然个体自己没有进行某一行为，但“镜像”其他个体的行为就能够引发镜像神经元的激活。那么如何利用具身认知方式来进行认知辅助工具的设计？

在游戏中，设置数轴的核心目的是让学生掌握数量大小的方向感，左边的数比右边的数小，越往右数字越大。本研究设定数轴的呈现方式是“数轴墙”，让数轴显示在一堵障碍墙上，游戏化身能够直接面对数轴墙，形成三个平行平面，即学习者平面、游戏化身平面和数轴墙平面，以此确保学习者、化身、数轴墙的左右方向的一致性。学习者借助游戏化身进行游戏参与，游戏化身的左右手方向与学习者左右手方向形成映射;在学习者的操控下，游戏化身与数轴墙进行交互，成为学习者与数轴墙交互的中介。基本设置内容是一根0～1范围的数轴，标有刻度0和1，其他刻度的标注依内容设计而定。

（三）分数表征

三重编码模型是认知神经科学领域广为接受的数字认知模型。基于数学认知在行为和脑神经机制方面的相关研究，该理论认为，大脑在进行数量加工任务时，会使用三种不同功能的编码对数量进行表征，包括模拟数量编码（Analog Magnitude Code）、听觉言语编码（Auditory Verbal Code）、视觉阿拉伯数字编码（Visual Arabic Code）。其中，模拟数量编码主要是指对代表数值概念的图形进行加工，如代表分数概念的带有阴影的图形;听觉言语编码是指对分数文字进行加工，如“三分之一”;视觉阿拉伯数字编码是指对阿拉伯数字的加工，如“1/3”。

在三重编码模型的理论基础上，为确保游戏的有效性，笔者对小学数学教材（人教版、北师大版）进行前期调研，发现数学教材的分数概念性讲授内容主要以模拟数量编码和视觉阿拉伯数字编码为主，并且模拟数量编码的分数图形以独立图形为主（如带有阴影的圆形或方形），集合图形为辅（如5片叶子中的2片）。为了兼顾编码的平衡以及中国小学数学教材的内容特点，游戏两类编码的比例设计尽可能匹配教材。

（四）知识模块框架

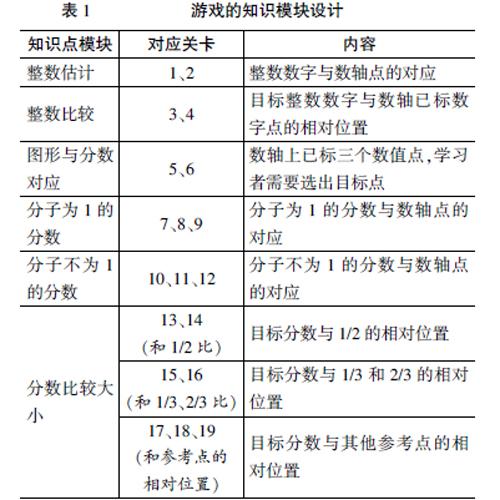
依据前文所述的数字发展的整合理论，数值理解是整合整数、分数、小数认知的关键。以数值理解的视角看，整数与分数一脉相承，都是数值的符号表达，分数表达了整数的可分割性。为了让儿童在学习分数之前，借助已有的整数知识，理解数值大小的方向性，本研究在分数内容之前设置了4个整数知识关卡。不仅可以让儿童尽快建立新旧知识的联系，也可以帮助儿童掌握游戏的玩法。小学数学教材的分数概念性知识的主要讲授方式是“数形结合”，因此，设置了图形与分数对应的关卡，此部分的主要目的是巩固“部分与整体”知识的学习。接下来，依据教材的知识点安排，设置了“分子为1的分数”“分子不为1的分数”“分数比较大小”的模块，具体内容见表1。

四、游戏元素的设计与理论参考

在科学性和有效性的基础上，游戏元素是实现教育游戏趣味性的关键。游戏元素的设计秉承认知中心的原则，围绕认知内容的设计展开，主要涉及游戏情境与交互方式、奖惩机制、声音设计、故事线设计等，下文主要介绍核心游戏元素的设计。

（一）游戏情境与交互设计

游戏情境与交互设计是教育游戏激发儿童学习动机的基础，也是游戏元素设计的核心。内在动机理论是游戏情境设计的主要参考。依据Malone和Lepper提出的游戏内在动机理论，挑战、好奇、控制、幻想能够影响学习者的内在动机;此外，集体动机受到合作、竞争、自尊因素的影响[19]。每一个数轴墙都是一个挑战任务，学习者需要通过自身的认知努力，撞击正确的数轴点，瞬间击碎数轴障碍墙，才能获得积分继续前进。如未能正确撞击，化身将受到猛烈反弹，并接受相应惩罚。为了适度地激发儿童的好奇心，数轴墙的高度高于游戏化身，通过遮挡视线的方式暗示只有完成挑战才能继续新空间的探索。在游戏化身的控制方面，学习者通过键盘的上下左右键来完全操纵化身，左右键控制方向，上下键控制速度，任务的成败完全取决于学习者的认知努力。同时，为了增加游戏的沉浸感，适当激发儿童对虚拟世界的幻想，游戏还设置了故事线元素，基于数轴墙的设计，围绕“绿光水晶墙”“科技水晶墙”“紫色玻璃墙”“森林墙”等展开，通过闯关获得宝藏。

（二）獎惩机制

在通过情境与交互激发学习动机的基础上，教育游戏需要一套完善的奖惩机制以维持动机水平，增加学习者的情感投入。ARCS动机模型是教育游戏奖惩机制设计的重要理论参考，该理论认为，人的行为取决于感知到的目标的可能性以及主观价值[20]，影响学生学习动机的因素主要包括“注意”“相关”“信心”“满足感”四个方面。在初始阶段，认知内容和游戏情境能够引发儿童的注意和兴趣，而信心和满足感的获得才能支持持续的学习行为。不断试错有助于获得信心和满足感，为了给儿童充足的试错机会，游戏的每一个关卡设置了10个数轴墙，即10个数轴任务。游戏场景左上角有7颗能量星，为7次试错机会，每错一次减少1颗能量星，以此确保每一个关卡的通关标准为正确率高于60%。与此同时，游戏为儿童提供多元的教学支架性质的方向提示。

学习科学领域的学者已达成共识，学习是认知、情绪与生理层面进行多层次交流的过程。积极的情绪有助于学习，消极情绪将会对学习带来消极影响。在逐步建立信心与满足感的过程中，教育游戏还需要通过一定的奖惩机制来调动学习者的情绪状态。研究发现，积极的情绪有助于促进记忆，例如，让实验参与者对照片呈现的愉悦程度进行评价，然后再进行照片内容的回忆，研究发现被试对带有明显情绪状态的图像有更加清晰的回忆[21]。

为了能够最大限度调动学习者的情绪投入，本研究参考认知神经科学领域对随机奖励的最新研究，在基础数轴任务积分的基础上，设计了“与运气相关”的随机奖励机制。认知神经科学领域发现，中脑区域的神经递质多巴胺与奖励活动有关，当灵长目动物意识到奖励出现的不确定性，脑中的多巴胺能的释放会达到峰值[22]。而多巴胺对整个大脑前额叶等脑区神经元的活性有重要影响[23]。因此，游戏设计将随机奖励纳入积分体系中，随机加分以随机金币形式出现，游戏化身在路上行走的过程中获得随机加分，每关随机奖励出现2～4次，奖励数值随机。其他积分要素还包括基础数轴任务积分以及剩余能量星。努力相关积分和运气相关积分的综合奖励设计旨在激发大脑多巴胺的分泌，保持游戏的不确定性，充分调动游戏化学习过程中的学习者情绪状态。为了更好地激发儿童的学习动机，游戏中还设置了积分排行榜的游戏元素，以此激发儿童的竞争欲望。

（三）声音设计

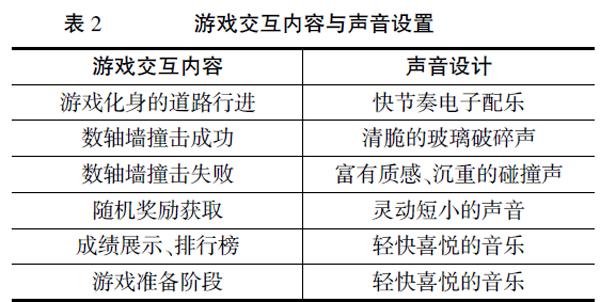
声音是多媒体传递信息、创造良好视听体验的重要元素。依据梅耶的多媒体认知理论，记忆由语言系统和视觉系统构成，记忆可以通过视觉编码和言语编码的联结实现强化，同时呈现视觉信息和言语信息有助于促进记忆。本研究决定对声音与游戏交互进行融合设计。具体声音与游戏交互的搭配设计，见表2。比较典型的声音设计是数轴墙的撞击声音，为了激发学习者的成就感，当游戏化身成功撞击数轴墙，游戏会出现响亮、清脆的玻璃破碎声。

五、游戏的应用效果

为检验分数游戏的应用成效，笔者在北京市顺义区的一所公立小学开展了为期一周的准实验研究，具体情况如下：

（一）研究方法与过程

本研究采用准实验方法，四年级的两个班共65名学生参加。参与学生每天在学校机房玩20分钟《分数跑跑跑》，玩五天，共100分钟。在实验周期的设计方面，基于分数游戏的教育目的，在连续一周的五天内进行游戏干预，与游戏的内容模块设计相匹配。

（二）研究工具

游戏化分数学习的应用效果测量包含两个维度，其一是围绕认知效果的分数概念性知识水平测试，其二是检验主体性体验的动机等问卷量表。为测量学生的分数概念性知识水平，参考国外相关研究的测评方法，本研究的测试题目主要来自三大权威题库，包括美国国家教育进展测评、国际数学与科学趋势评估、美国加州标准测试。试题共有47道，每题1分，共47分。其中，第一类题目考察的知识是“分数与图形”，共15道题;第二类题目考察的知识是“分数与数轴”，共15道;第三类题目考察的知识是“分数比较大小”，共17道。前测、后测所用题目相同。题目类型主要包括选择题和填空题，代表性测试题目如图2所示。

为全面考察分数游戏的应用效果，本研究使用相关量表以考察主体性体验，包括内在数学焦虑量表（The Modified Abbreviated Math Anxiety Scale）和动机量表（Intrinsic Motivation Inventory）。数学焦虑量表修正版是数学焦虑量表（AMAS）的缩略版。原量表共9个题目，在对问卷进行信效度分析之后，保留包含“测评焦虑”和“学习焦虑”两个维度的8个题目（Cronbach's alpha=0.868），采用5点李克特量表的自我报告方式。内在动机量表旨在测量学习者的兴趣（Interest）、胜任力感知（Perceived Competence）、努力程度（Effort）等主观感受。原始量表共涉及7个维度，本研究选取了和游戏化学习关系密切的两个维度，“胜任力感知”和“兴趣”（Cronbach's alpha=0.893）。该问卷采用5点李克特量表自我报告的方式。本研究所用问卷见表3。

（三）应用研究结果

在认知效果方面，数据结果显示，在游戏化分数学习干预之前，前测总成绩均值为23.83，标准差为7.8;第一类题目的前测成绩均值为11.65，标准差为2.48;第二类题目的前测成绩均值为7.23，标准差为3.59;第三类题目的前测成绩均值为5.70，标准差为3.62。在一周的游戏化分数学习干预之后，后测总成绩均值为30.44，标准差为7.68;第一类题目的后测成绩均值为12.45.标准差为2.36;第二类题目的后测成绩均值为8.53，标准差为3.36;第三类题目的后测成绩均值为9.46，标准差为4.03。配对样本T检验结果显示，后测总成绩均值显著高于前测[t（64）=9.593，p=0.00]，第一类题目的后测成绩均值显著高于前测[t（64）=3.793，p=0.00]，第二类题目的后测成绩均值显著高于前测[t（64）=3.323，p=0.001]，第三类题目的后测成绩均值显著高于前测[t（64）=8.86，p=0.00]。

在主体性体验方面，数据结果显示，在游戏化分数学习干预之前，数学焦虑量表的测评维度的前测均值为2.3，标准差为1.09;学习维度的前测均值为2.09，标准差为1.07;数学焦虑量表整体前测均值为2.19，标准差为0.99。在一周的游戏化分数学习干预之后，数学焦虑量表的测评维度的后测均值为2.29，標准差为0.95;学习维度的后测均值为2.05，标准差为0.81;数学焦虑量表整体后测均值为2.17，标准差为0.8。配对样本T检验显示，数学焦虑量表子维度及整体前后测的均值无显著差异（p>0.05）。在游戏化分数学习干预之前，数学学习内在动机量表的胜任维度的前测均值为4.02，标准差为0.72;兴趣维度的前测均值为4.1，标准差为0.82;量表整体前测均值为4.05，标准差为0.67。在一周的游戏化分数学习干预之后，内在动机量表的胜任维度的后测均值为3.89，标准差为0.82;兴趣维度的后测均值为4.2，标准差为0.86;数学学习内在动机量表整体后测均值为4.03，标准差为0.71。配对样本T检验显示，内在动机量表子维度及整体前后测的均值无显著差异（p>0.05）。

总体而言，《分数跑跑跑》能够显著提高四年级学生的分数概念性知识水平。学生在考察分数概念理解程度的“部分与整体”（第一类测试题目）与“测量解释”（第二类、第三类测试题目）后测中都有良好的表现。但与此同时，为期一周的游戏化学习体验未能显著降低四年级学生的数学焦虑水平，未能显著提升学习动机水平。

六、结论与讨论

本研究針对游戏化学习研究领域的核心问题——如何设计科学、有效、有趣的教育游戏，围绕基础教育阶段的分数认知，以学习科学的跨学科视角进行数学游戏《分数跑跑跑》的设计开发。由于教育游戏兼具教育目的和娱乐目的，教育目的是教育游戏的根本目标，“娱乐”以服务“教育”为核心宗旨，因此，教育游戏在认知内容上的科学性直接决定了教育游戏的使用价值。在教育游戏的科学性设计方面，应当坚持“立足跨学科视角的认知支持”原则，依据学习科学领域的相关研究成果进行认知内容的设计。在科学性的基础上，教育游戏需要着眼于实际问题，秉承“着眼教学实践的设计驱动”原则，以实践需求作为设计导向，确保教育游戏能够有效地应用于教育教学。在保障科学性和有效性的基础上，教育游戏可以借助游戏元素，充分调动学习者情绪，运用“借助情绪调动的动机发展”原则进行趣味性的设计。科学性、有效性与趣味性的层级关系与设计原则如图3所示。

在教育游戏的科学性方面，依据游戏化学习体验框架，基于情境的认知体验设计主要参考认知神经科学、教育学、心理学在分数认知方面的研究成果，确定游戏的核心认知内容为分数概念性知识的测量解释，以数轴作为核心认知辅助工具，参考三重编码模型和数字发展的整合理论，分别设计了游戏中的分数表征和知识模块框架。与此同时，为了保证教育游戏应用的有效性，在内容设计的过程中，统筹考虑国家课程标准要求、教材元素、学生水平进行内容设计。趣味性主要涉及基于动机的主体性体验，基于动机理论设计了游戏情境和交互方式，结合关于情绪的相关研究设计了兼顾“努力”和“幸运”的奖惩机制，并且围绕游戏元素设计了不同的声音效果。基于65名四年级学生的准实验数据结果，可以发现《分数跑跑跑》能够显著提高四年级学生的分数概念性知识水平。

回顾教育游戏在过去几十年间的发展历程，不难发现，技术发展确实为教育创新带来了前所未有的机遇。游戏技术成功实现了虚拟化的认知情境创建，为学习者提供了即时、有效的信息反馈，也让寓教于乐的理念得到了更加广泛的认可，虚拟现实等新兴技术也似乎展示了未来游戏化学习的无限可能。然而，机遇与挑战并存，虽然游戏化学习是当前的研究热点之一，教育游戏研究者终究需要回答“如何设计科学、有效、有趣的教育游戏”这一问题。以学习科学的跨学科视角进行教育游戏的设计开发具有巨大优势。认知神经科学、教育学、心理学等关于学习基础机制的研究成果为教育游戏的认知内容和游戏元素的设计提供了参考。通过技术设计的方式，架起沟通基础研究与教学实践的桥梁，为解决教学实践中的实际问题提供优质的游戏化学习资源。

[参考文献]

[1] LIAO C Y， CHANG W， CHAN T. The effects of participation， performance， and interest in a game-based writing environment[J]. Journal of computer-assisted learning， 2018， 34（3）： 211-222.

[2] 陈博殷，钱扬义，李言萍.游戏化学习的应用与研究述评——基于国内外课堂中的“化学游戏化学习”[J].远程教育杂志，2017，35（5）：93-104.

[3] 李秀晗，曲茜美.游戏化学习在儿童数字化阅读中的设计研究[J].电化教育研究，2018，39（12）：116-122.

[4] 徐杰，杨文正，李美林，等.国际游戏化学习研究热点透视及对我国的启示与借鉴——基于Computers & Education （2013—2017）载文分析[J].远程教育杂志，2018，36（6）：73-83.

[5] 张露，尚俊杰.基于学习体验视角的游戏化学习理论研究[J].电化教育研究，2018，39（6）：11-20.

[6] BANDURA A. Social cognitive theory： an agentic perspective[J]. Annual review of psychology， 2001， 52（1）： 1-26.

[7] HECH S A. Toward an information-processing account of individual differences in fraction skills[J]. Journal of educational psychology， 1998， 90（3）： 545-559.

[8] HECHT S A， VAGI K J. Sources of group and individual differences in emerging fraction skills.[J]. Journal of educational psychology， 2010， 102（4）： 843-859.

[9] FUCHS L S， SCHUMACHER R F， STERBA S K， et al. Does working memory moderate the effects of fraction intervention？ An aptitude-treatment interaction.[J]. Journal of educational psychology， 2014， 106（2）： 499-514.

[10] BOOTH J L， SIEGLER R S. Developmental and individual differences in pure numerical estimation.[J]. Developmental psychology， 2006， 42（1）： 189-201.

[11] CHARALAMBOUS C Y， PITTA-PANTAZI D. Drawing on a theoretical model to study students' understandings of fractions[J]. Educational studies in mathematics， 2007， 64（3）： 293-316.

[12] 辛自強，张睆.儿童的分数概念理解的结构及其测量[J].心理研究，2012，5（1）：13-20.

[13] 尚俊杰，张露.基于认知神经科学的游戏化学习研究综述[J].电化教育研究，2017（2）：104-111.

[14] JACOB S N， NIEDER A. Notation-independent representation of fractions in the human parietal cortex[J]. Journal of neuroscience， 2009， 29（14）： 4652-4657.

[15] LORTIE-FORGUES H， TIAN J， SIEGLER R S. Why is learning fraction and decimal arithmetic so difficult？[J]. Developmental review， 2015， 38： 201-221.

[16] SIEGLER R S， FAZIO L K， BAILEY D H， et al. Fractions： the new frontier for theories of numerical development[J]. Trends in cognitive sciences， 2013， 17（1）： 13-19.

[17] SIEGLER R S， THOMPSON C A， SCHNEIDER M. An integrated theory of whole number and fractions development[J]. Cognitive psychology， 2011， 62（4）： 273-296.

[18] ISCHEBECK A， SCHOCKE M， DELAZER M. The processing and representation of fractions within the brain an fMRI investigation[J]. NeuroImage， 2009， 47（1）： 403-413.

[19] MALONE T W， LEPPER M R. Making learning fun：a taxonomy of intrinsic motivations for learning[M]//SNOW R E， FARR M J. Authentic learning environments. London： Routledge， 1987：223-253.

[20] 柴亚军.ARCS动机模型在课堂教学中的应用研究[J].中国教育技术装备，2017（23）：6-8.

[21] ANTONENKO P D， VANGOG T， PAAS F. Implications of neuroimaging for educational research[M]//SPECTOR J M， MERRILL M D， ELEN J， et al. Handbook of research on educational communications and technology. New York： Springer， 2014：51-63.

[22] 周加仙.教育神经科学与信息技术的跨学科整合研究——访英国著名教育神经科学家保罗·霍华德·琼斯教授[J].开放教育研究，2016（6）：4-10.

[23] 李澄宇，杨天明，顾勇，等.脑认知的神经基础[J].中国科学院院刊，2016，31（7）：755-764.