粉煤灰混凝土强度与成熟度计算模型研究

2021-10-14吴翔

建筑施工 2021年6期

吴翔

海南省沪建建设有限公司海南海口 570105

混凝土被应用于工程中已有百余年的历史，依据我国近期的不完全统计，混凝土每年的用量约为10亿 m3[1]。作为混凝土中的主要胶凝材料——水泥，其生产过程中的粉尘是对环境造成破坏的重要污染物。为降低水泥制备与应用中带来的负面影响，众多学者开始聚焦可用于替代水泥的矿物掺合料的相关研究。以工业废渣或天然的矿物质材料为原料的矿物掺合料能填充胶凝材料的孔隙，参与胶凝材料的水化，改善混凝土的界面结构，提升混凝土的强度和耐久性。

其中，粉煤灰（飞灰）作为一种热电工厂废料，它的掺入不仅可以保证混凝土的质量，降低制造混凝土的成本，同时还提高了和易性、耐久性以及后期强度，因而成为世界各国使用最广的替代品。但粉煤灰的大量掺入将会对混凝土强度发展产生显著的影响。混凝土强度是影响混凝土施工质量的关键，更是顺利开展结构设计与施工的核心因素。因而建立可预估粉煤灰混凝土强度的显式计算公式显得极为迫切。

水泥种类、骨料粒径、骨料类型等因素都可能影响混凝土的强度，但确定混凝土配合比及其施工工艺后，混凝土强度的增长将仅与养护温度及龄期相关。在浇筑施工大体积混凝土的过程中，混凝土强度的发展与结构裂缝的产生受温度的影响较大，且其抗压强度与温度时积（温度与时间的乘积）呈现正比关系，故成熟度这一概念被提了出来。

采用成熟度方法可实时、无损估测混凝土结构的强度，是一种综合考虑时间与温度对混凝土强度演化影响的技术，为混凝土结构强度的实时评估提供了一种相对简单的评价手段。

目前，国内外学者已成功建立了不同类型的基于成熟度的混凝土抗压强度计算模型，然而此类模型中并未考虑粉煤灰掺量、水胶比以及水泥强度的作用。因此，本研究基于前人大量的试验数据，分析粉煤灰混凝土的成熟度和抗压强度之间的变化规律，为利用成熟度预测粉煤灰混凝土的抗压强度提供依据。

1 混凝土成熟度算法及与强度关系

Saul[2]认为配合比一定的混凝土，只需成熟度相等，其强度也应相等。因而，提出了成熟度（maturity）的理念，即温度与龄期的乘积，如图1所示。至此，便出现了Saul成熟度方程：

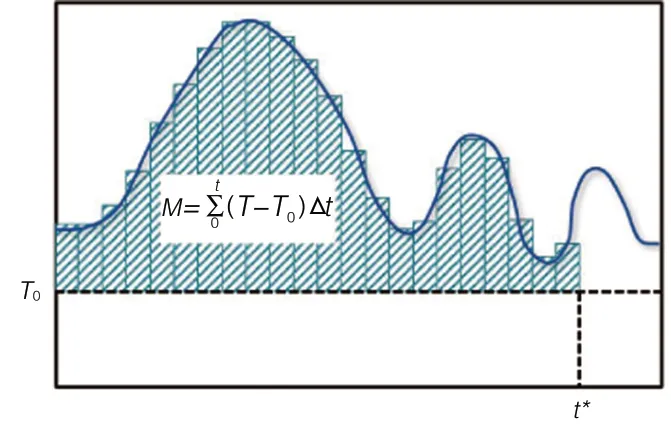
图1 基于Nurse-Saul成熟度方程的时间-温度示意[3]

式中：M——成熟度，℃·h或℃·d；

T——时间间隔Δt内混凝土平均温度，℃；

T0——基准温度，℃，通常取－10 ℃；

Δt——时间间隔，h或d。

混凝土性能的改变可使用成熟度进行间接表征，然而二者间尚未形成普适化的理论公式，Carino[4]认为比较经典的有3种，如表1所示。

表1 强度-成熟度关系式[4]

2 构建成熟度-强度模型

考虑到不同试验结果存在着离散性问题，本文尽力将前人关于粉煤灰混凝土研究的相关数据进行筛选汇总。其选取规则是：

1）强度的测定方法遵循GB/T 50081—2002《普通混凝土力学性能试验方法标准》中的测试要求与步骤，强度值为标准150 mm3立方体试件所得结果或将其他尺寸试件的结果进行转换。

2）混凝土中的矿物掺合料均为单掺粉煤灰。

3）混凝土中仅掺入奈系或聚羧酸减水剂，无早强剂、引气剂、缓凝剂等。

将文献[5-17]中报告的粉煤灰混凝土强度统一转化为150 mm3立方体混凝土强度，随后将各龄期粉煤灰混凝土的抗压强度值除以其对应的28 d强度，得到相对强度（fr）。同时，将各龄期数据以及养护温度数据代入式（1）中，即可得到各龄期粉煤灰混凝土的成熟度。OPC混凝土，即无粉煤灰掺入的混凝土，相对抗压强度-成熟度关系如图2所示。

图2 OPC混凝土相对强度-成熟度曲线

将OPC混凝土的相对抗压强度-成熟度关系式作为基准，使用前述3种经验公式进行拟合，结果显示3种关系式均可较好地表征成熟度-强度间的演化规律，且双曲线关系式的拟合度更高。因此，本文后续将应用双曲线关系式表述粉煤灰混凝土相对强度-成熟度间的关系〔式（2）〕。

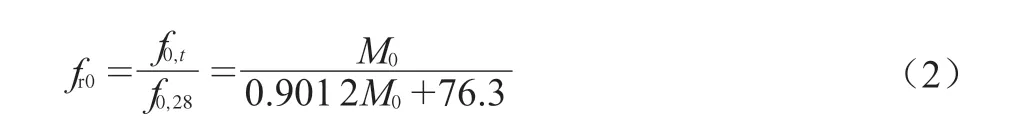
式中：fr0——OPC混凝土相对抗压强度；

f0,t——OPC混凝土龄期为时的抗压强度，MPa；

f0,28——OPC混凝土28 d抗压强度，MPa；

M0——OPC混凝土成熟度，℃·d。

以OPC混凝土相对抗压强度-成熟度曲线为基准式，则不同掺量粉煤灰混凝土相对强度与成熟度之间的关系可以表达为：

式中：fr——粉煤灰混凝土相对抗压强度；

ft——粉煤灰混凝土龄期为t时的抗压强度，MPa；

f28——粉煤灰混凝土28 d抗压强度，MPa；

M——粉煤灰混凝土成熟度，℃·d；

α——与粉煤灰掺量相关的经验参数。

α与粉煤灰掺量（RFA）间的关系如式（4）所示，可决系数R2可达0.950 1。

因而，结合式（3）与式（4）即可计算得到不同掺量粉煤灰混凝土相对抗压强度，试验所得的相对抗压强度与计算所得的相对抗压强度对比如图3所示。

从图3中可以看出，计算所得的相对抗压强度与试验所得的相对抗压强度相差不大，约在±20%的误差范围内变动。因此，可以采用式（3）与式（4）计算相对抗压强度。

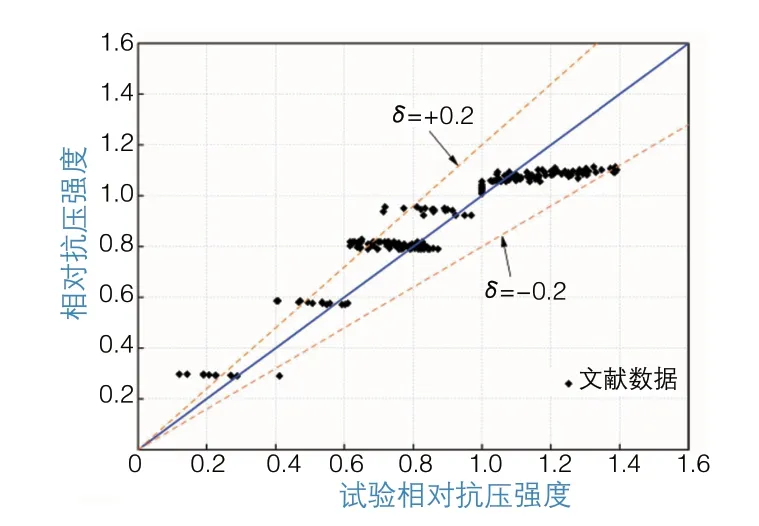
图3 试验相对抗压强度与计算相对抗压强度对比

粉煤灰的应用始于20世纪60年代，随后研究者进行了粉煤灰对混凝土强度影响的相关研究，建立了各种预测模型。国外最早曾改进Bolomey公式对粉煤灰混凝土的强度进行估算〔式（5）〕，此公式考虑了水胶比对强度的影响。

式中：fc——粉煤灰混凝土的抗压强度；

C、F——水泥与粉煤灰用量，kg/m3；

A、B——适用于粉煤灰混凝土的常数。

随后Popvics[18]、Hedegaard与Hansen[19]等的研究发现，粉煤灰混凝土的强度与水胶比以及粉煤灰的掺量二者有关，因而在Bolomey改进公式的基础上各自建立了强度与水胶比以及粉煤灰掺量的关系式。

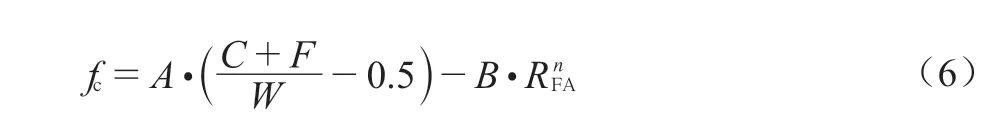
式中：A、B、n——按ASTM C192或C39确定的经验常数；

RFA——粉煤灰掺量百分数，%。

式中：A、B、E——经验常数。

混凝土的强度受到水泥、骨料、界面过渡区强度及其综合效应的影响，Liu等[20]的研究表明，粉煤灰混凝土的强度与水泥强度呈现正相关关系。

赵飞宇等[21]在此基础上提出将水胶比（RW/B）、粉煤灰掺量（RFA）及水泥强度（fce）3种因素考虑在内的粉煤灰混凝土多因素计算模型。

式中：α1、α2、α3、α4——经验常数。

因此，本文以水胶比、粉煤灰掺量及水泥强度为模型建立参考因素，建立28 d粉煤灰混凝土强度公式。以RW/B与RFA作为自变量，f28/fce为因变量，将搜集到的文献中数据进行回归分析，可得式（9），可决系数R2可达0.871。

联立式（3）、式（4）以及式（9）即可建立粉煤灰混凝土强度-成熟度间关系式：

3 强度-成熟度模型验证

3.1 原材料

试验所用水泥为江苏扬州绿杨水泥发展有限公司生产的“绿杨牌”P·O 42.5水泥，该水泥的基本物理力学性能如表2所示。砂为天然河砂，属于中砂，细度模数为2.70；粉煤灰选用华能Ⅱ级粉煤灰，其物理力学性能如表3所示。石子为产自扬州的粒径5～16 mm连续级配的碎石；水为自来水。

表2 水泥的基本物理力学性能

表3 粉煤灰物理、化学性能

3.2 试验配合比

选用不同粉煤灰掺量的混凝土配合比进行试验，配合比采用的胶凝材料总量为433 kg/m3；粉煤灰的掺量为0、20%、30%和40%。所用配合比如表4所示。

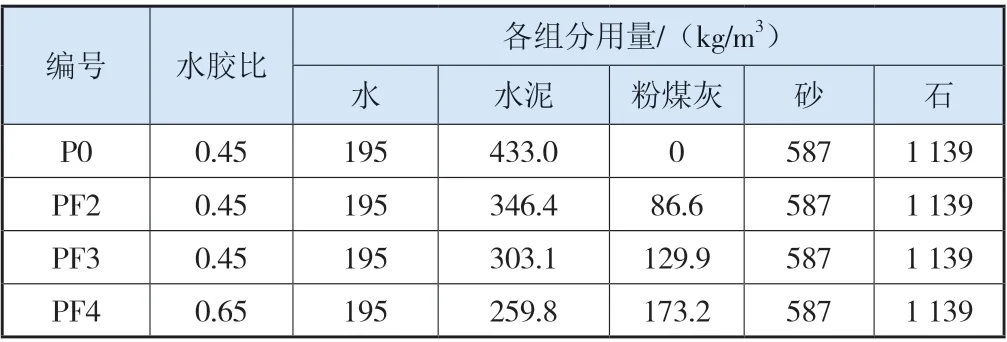
表4 混凝土配合比

3.3 试验结果与模型验证

采用尺寸为100 mm×100 mm×100 mm的立方体试件进行试验，在试件成形后带模标准养护24 h后脱模，脱模后置于（20±3） ℃的恒温恒湿养护室中进行养护。当试件的龄期为7、14及28 d时进行标准抗压强度测试。混凝土抗压强度指标测定遵循GB/T 50081—2002《普通混凝土力学性能试验方法标准》。此次试验测试的结果如表5所示。

从表5中可以看出，在相同养护龄期时，粉煤灰掺量越高，其早期强度相对越低。将本次试验参数代入式（10）中计算粉煤灰混凝土抗压强度，同时为了验证模型是否能够准确预测大掺量粉煤灰强度以及粉煤灰混凝土的长期强度，将王成启等[22]的试验参数也代入式（10）中，计算结果如图4所示。

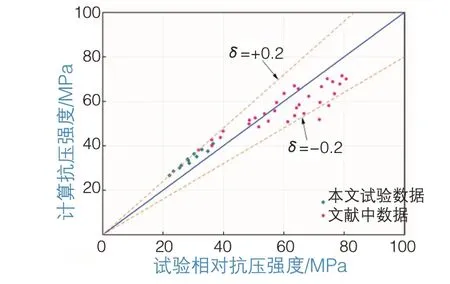
图4 模型预测结果

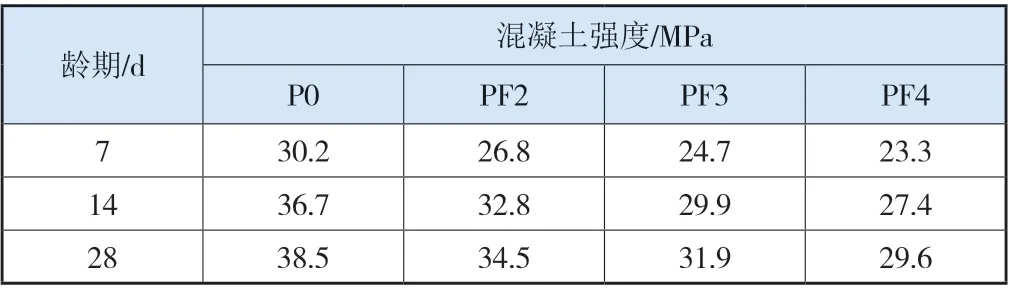
表5 粉煤灰掺量不同的混凝土配合比试验结果

从图4中可以看出，本文所得模型能够较好地预测试验结果以及文献中的试验数据。同时，计算结果表明：当粉煤灰混凝土处于早龄期时，模型预测的试验结果偏大，而随着龄期的增长，粉煤灰混凝土的预测强度偏小。这是因为粉煤灰的掺量增加使得混凝土中水泥熟料的水化产物Ca（OH）2含量降低，致使粉煤灰水化环境劣化，进而降低混凝土的强度；当混凝土的龄期进一步增长时，粉煤灰的水化反应程度逐渐加快，因而混凝土内部结构更加紧密，提升了后期混凝土强度。所建立的模型中并未考虑此种因素的影响，因而导致预测结果存在偏差。