考虑土体强度非线性的地震主动土压力分析

彭晓钢 王寰宇 李有志

1. 深圳市天健（集团）股份有限公司 广东 深圳 518034；2. 中南大学土木工程学院 湖南 长沙 410075

岩土体主要由土骨架、孔隙水和空气组成，由于自身组成复杂，导致其在试验中表现出来的强度特征相对复杂。在常规的三轴试验中，可以发现岩土体所处的应力状态也直接影响抗剪强度指标。其中，随着围压的增大，内摩擦角减小而黏聚力增大。

因此，在不同的应力条件下，岩土体的抗剪强度指标表现出较大的差距。另一个角度，岩土体材料因固有特性，其所处的应力状态对强度具有较大的影响，非线性特征较为明显。

对于岩土体所表现出来的非线性特征，解决方案通常为采用非线性强度准则来描述强度特性。而非线性强度准则主要有以下2类：

1）以Mohr-Coulomb强度准则为代表的采用法向应力和剪切应力形式描述的强度准则。

2）以Hoek-Brown强度准则为代表的采用主应力形式描述的强度准则。

尽管在参数的含义上，以上2类强度准则存在一定的差别，但是其数学表达式通常为幂指数形式。本节将着重介绍Mohr-Coulomb强度准则及其参数选取的方法。

在实际抗震设计中，PGA（峰值加速度）常用来描述地震动，即以静力计算为基础，将地震的作用简化为一个惯性力系附加在研究对象上，这就是最常见的拟静力法。拟静力法凭借简单、易实现的特点被广泛应用在岩土工程稳定性分析中[1-4]，不足的是该方法忽略了地震波的空间变化和时变特性。因此，拟静力法给出的解往往相对保守。

目前，加速度时程分析是比较可靠的方法之一[5-6]。但是该方法过于复杂，在数值模拟中应用较多，难以在理论分析中进行拓展[7-9]。

地震波是由多种波叠加而成的复杂波，无法用函数进行准确刻画。在此背景下，通过考虑振幅和相位等其他参数随着地震波在传播过程中变化的特征，提出了拟动力法。在现有研究中，该方法主要用于基于极限平衡法的侧向土压力计算[10]。

该方法中所采用的加速度分布形式可以是符合实际情况的任何形式。但为简化起见，在大多数研究中，都采用正弦加速度且没有考虑初始相位差[11]。关于挡土墙主动土压力，已经有很多学者开展过研究[12-13]，本文主要基于极限分析上限定理，建立对数螺旋线破坏机构，并计算内外力功率，建立功能平衡方程，求解最优上限解。研究结果可为工程设计与施工提供参考。

1 基本原理

1.1 广义切线技术

非线性强度准则有多种形式，但对土体材料而言，非线性强度准则通常表示成如下幂指数形式：

式中：c0——土体初始黏聚力；

σt——土体的抗拉强度；

σn、τ——极限破坏面上的正应力和剪应力；

m——非线性系数。

为便于计算，针对非线性Mohr-Coulomb强度准则，提出了一种切线技术，用以分析岩土工程中的稳定性问题。Yang[14]表示，该切线的上限解为真实极限荷载的一个严格上限值，拓展了广义切线技术在极限分析方法中的应用。对于强度包络线上的任意一点，切线方程为：

式中：ct、φt——等效的黏聚力和内摩擦角。

根据几何关系和公式（1），可将土体等效内摩擦角正切值和等效黏聚力写成如下等式：

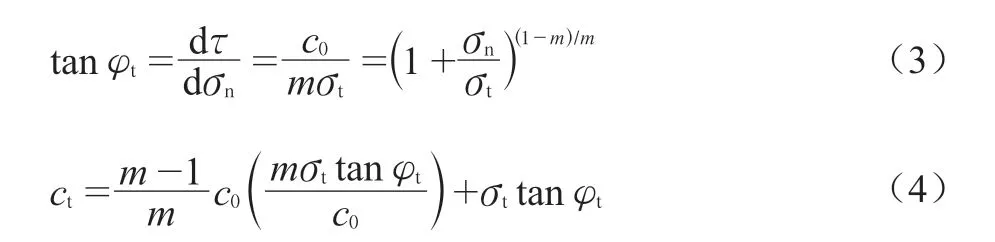
在实际计算时，需要通过穷举算法优化φt得到最不利的切线，使目标函数取得最优上限解。

1.2 拟动力法

在考虑地震作用时，横波和纵波的速度可以分别表示为VP＝[2G（1-v）/ρ（1-2v）]0.5和Vs＝（G/ρ）0.5，其中G是剪切模量，v是泊松比，ρ为土体密度。对于大多数土体而言，其泊松比v＝0.3，此时VP/Vs＝1.87。

本文忽略横波和纵波之间的周期差异，认为横波和纵波周期相同。加速度采用正弦波进行输入，作用在回填的同一高度位置上时，水平加速度和垂直加速度之间通常存在相位差。

同时，需要指出的是，在地震期间，随着地震波接近回填土表面，地震动将被放大。因此，引入加速度幅值放大系数加以考虑。

水平加速度和垂直加速度分别为正弦波，kh、kv分别为水平地震系数和垂直地震系数。因此，时间为t时，yi处的地震加速度根据拟动力法可以写成如下表达式：

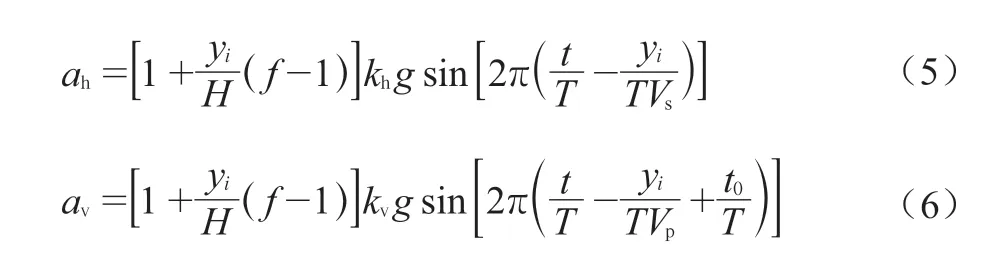
式中：Vs、Vp——横波和纵波的波速；

f ——土体放大系数；

t0——回填土底部水平加速度与垂直加速度之间的初始时间差。

2 主动土压力能耗分析

2.1 重力功率计算

根据极限分析上限法的要求，通常根据速度相容场去描述破坏机构，在软土中，常采用旋转模式的破坏机构。同时，为满足相关联流动法则的要求，速度间断面上任意一点的切线方向与其速度方向的夹角为材料的内摩擦角φ。据此，破坏面方程在极坐标中可以表示成以下函数：

式中：r0、θ0——初始半径和初始角度。

如图1所示，初始参数：墙高为H，墙背与水平面夹角为β，墙后填土重度为γ，摩擦角为φ，黏聚力为c。图1中L为A、B两点的距离，通常有如下关系式：

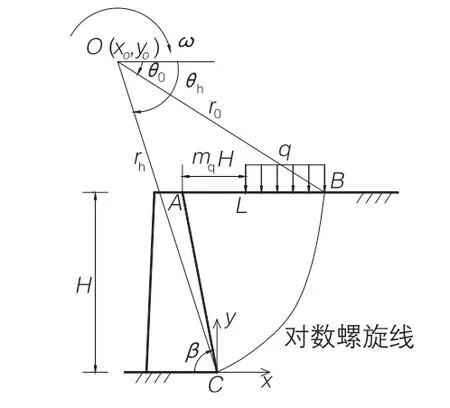
图1 挡土墙破坏模型示意

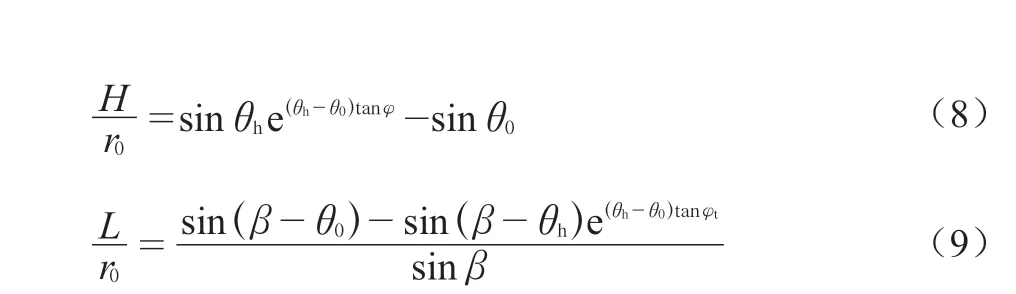
本文考虑的外荷载包括土体自重、地震惯性力、坡顶附加均布荷载以及挡墙的主动土压力。在计算重力功率时，采用叠加法计算，先分别求出块体OBC、块体OAC、块体OAB的重力功率值W1、W2、W3，再通过简单的代数加减，可得ABC的重力功率为：W1－W2－W3。块体OBC的重力功率可以通过以下公式进行积分：

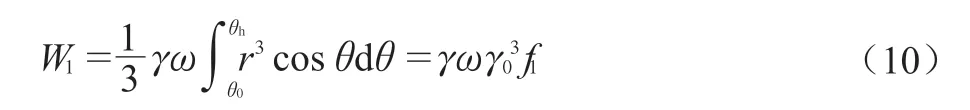
同理，块体OAC和OAB的功率也可算出，通过叠加可得到总的重力做功功率：

f1，f2，f3为无量纲函数，具体如下：

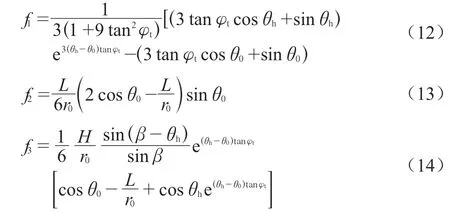
2.2 地震力功率计算

由于拟动力法考虑了加速度随时间和空间变化的特性，故上述积分方法不再适用于计算地震力功率，需要采用水平分层的方法进行计算。在此，提出了一个无限小的梯形单元QiQi+1Pi+1Pi来适应这种变化。以图2所示的微元为例来说明获得惯性力功率的方法。

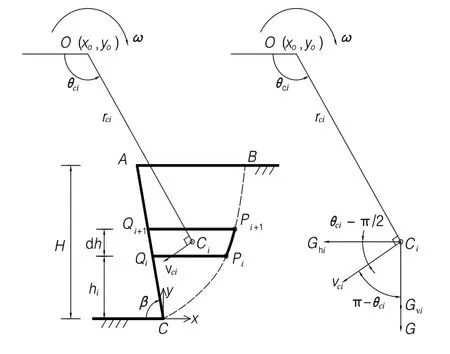
图2 梯形单元惯性力计算示意

首先，在高度为hi和hi＋d h处分别有2条虚拟水平线，分别求出其与对数螺旋面、墙面的交点，分别为Pi（xi, yi）、Qi（x′i, y′i）、Pi+1（xi+1, yi+1）、Qi（x′i+1, y′i+1），通过几何关系可以推导出其坐标值，其中滑移面上Pi点的横坐标需满足以下方程：

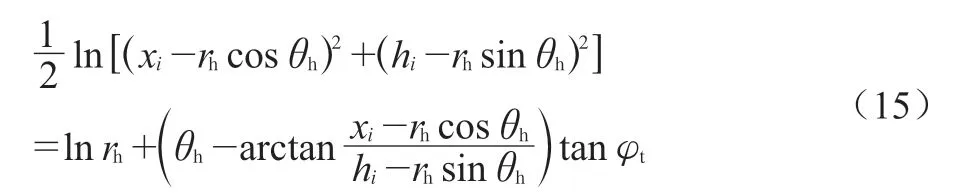
为计算各微元的惯性力引起的功率，必须确定该微元的面积及其重心。根据梯形元素的几何特性，给出重心坐标Ci（xci, yci）和该微元的面积Si，因此，可以推算出该微元惯性力的功率并且可以通过对每个微元求和来计算整个破坏机构的惯性力功率：

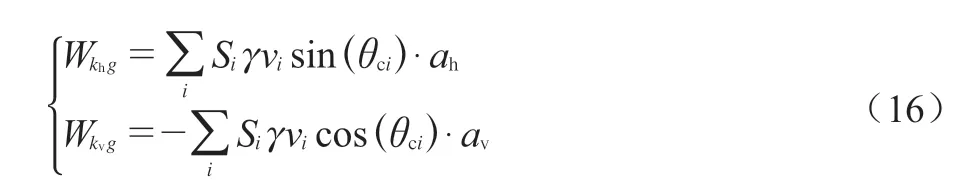
其中，θci是相对于旋转中心点的旋转角度。

当地震波速趋近于无穷大时，拟动力法则退化为拟静力法，由于加速度系数kv、kh在任意空间位置、任意时间下均为一常数，可以采用与重力功率同样的计算方法进行求解。

2.3 附加荷载功率计算

本文墙后填土作用有均匀分布荷载，如图2所示，破坏机构范围之外的荷载不予考虑。为考虑附加载荷在地震影响下的惯性效应，水平和垂直惯性力都作用在回填土表面上。在这种情况下，可以获得附加荷载引起的功率为：

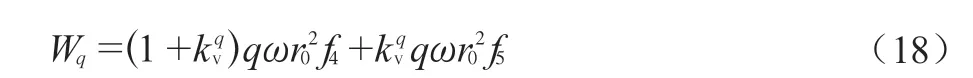
无量纲函数 f4、f5如下：

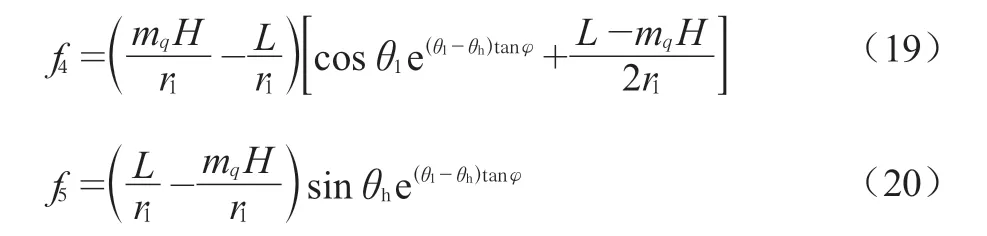
2.4 主动土压力功率计算

在计算主动土压力引起的功率时，应事先确定合力的作用点和方向。现有的大量研究表明土压力合力的作用点位于墙高的1/3处，并且采用墙-土的摩擦角来描述力的方向。对土压力合力分别进行正交分解得到其水平分量和垂直分量：

其中，δ是墙-土的摩擦角，进而可以求出主动土压力的功率如下：

无量纲函数 f6如下：

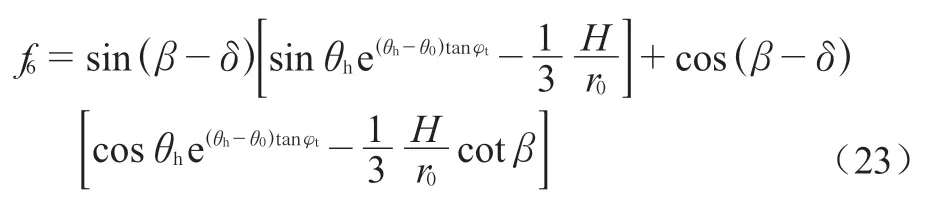
其次，墙-土接触面的附着力也是外力功率的一部分，单位长度的附着力为cttanδ/tanφt，其功率由下式计算可得：

无量纲函数f7如下：

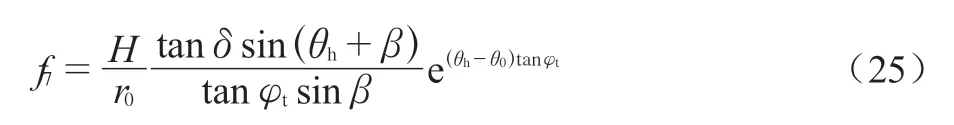
2.5 内能耗散率计算

破坏机构为刚性块，内部能量将仅沿着破坏面发生耗散。基于能量耗散率是剪切力和速度的点积的定义，可对速度间断面进行径向微分，每个径向微分长度为rdθ/cosφt，黏聚力为ct，速度间断面在该处的切向速度为ωrcosφt。总的内部能量耗散率可以沿着速度间断面进行积分求得：

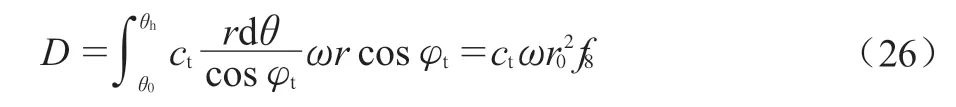
无量纲函数f8如下：

2.6 目标函数求解

地震主动土压力的上限解可以通过将由外力完成的功率等于总内部能量耗散率来得出。其功率平衡方程为：

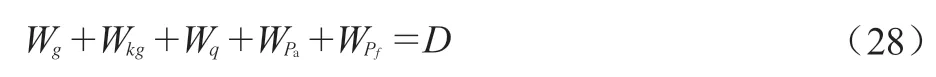
因此，地震主动土压力的表达式可以写为：

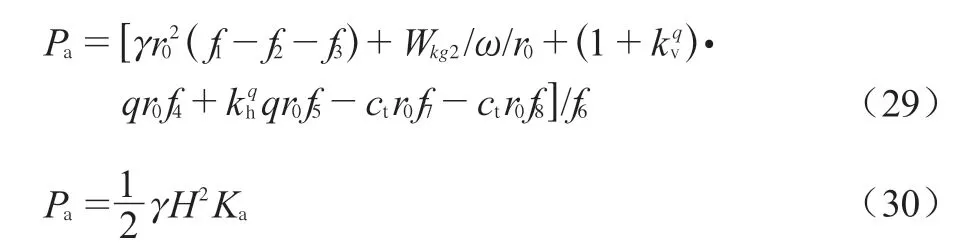
基于不同的破坏机构产生不同土压力结果的事实，且破坏机构取决于旋转中心的位置，初始相位差和切线法中优化变量φt均会对结果造成影响。因此，主动土压力系数可以表示为上述4个独立变量的函数Pa＝f（θ0, θh, t , φt）。最终结果将通过优化获得。

为确保破坏机构有效，优化过程必须满足下面的约束条件：

3 研究结果与分析

3.1 初始黏聚力对主动土压力的影响

初始黏聚力作为非线性强度准则中重要的强度参数，其力学含义是指破坏面在无任何正应力下材料的抗剪强度。为研究其对主动土压力的影响，通过计算，得到当非线性系数m＝1.2～2.0时，主动土压力Pa随初始黏聚力c0变化的规律，如图3所示。

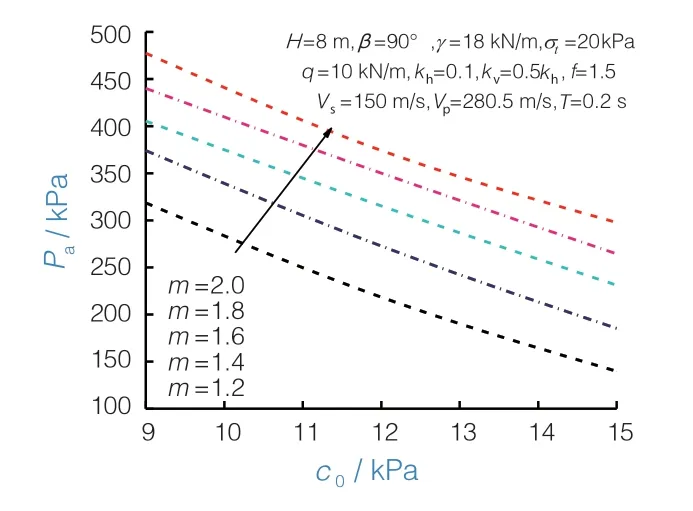
图3 初始黏聚力对主动土压力的影响

从图3可以看出，初始黏聚力对主动土压力有较大的影响。随着初始黏聚力的增加，主动土压力逐渐降低，且其变化趋势近似为线性。这与我们现有的认知是一致的，即黏聚力的增加有利于墙后填土的稳定。从图3中还可以看出，随着非线性系数m从1.2变化到2.0，主动土压力逐渐增大，但其增大的速度随着m的增大而逐渐变缓。

3.2 单轴抗拉强度对主动土压力的影响

为研究单轴抗拉强度对主动土压力的影响，通过计算得到当非线性系数m＝1.2～2.0时，主动土压力Pa随单轴抗拉强度σt变化规律如图4所示。

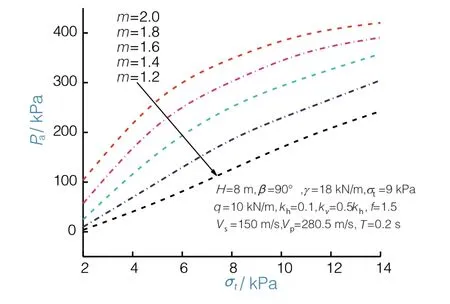
图4 单轴抗拉强度对主动土压力的影响

从图4可以看出，单轴抗拉强度对主动土压力影响显著。当非线性系数发生变化时，主动土压力随单轴抗拉强度的变化趋势略有不同。但总体来说，随着单轴抗拉强度的增加，主动土压力是逐渐增大的。所以实际上，土体的单轴抗拉强度不利于墙后填土的稳定。这一点也能从计算边坡安全系数来研究其稳定性看出来，更高单轴抗拉强度会得到更低的安全系数。

3.3 水平地震系数对主动土压力的影响

水平地震系数作为考虑地震效应最重要的参数之一，在研究其他拟动力法参数的影响之前首先需要明确其对主动土压力的影响。通过计算得到当附加荷载时，主动土压力随水平地震系数变化的规律，如图5所示。

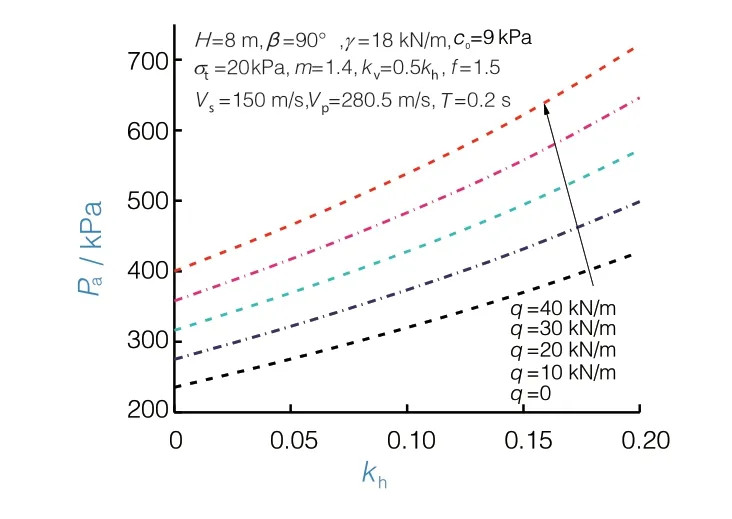
图5 水平地震系数对主动土压力的影响

从图5中可以看出，当水平地震系数从0变化到0.2时，主动土压力增大约1.8倍。随着水平地震系数的增大，主动土压力逐渐变大，且其增大速率略微增大。随着附加荷载的增大，主动土压力也呈现出线性增大的特征。上述2个特征可以为活跃地震带区域的高路堤支护提供一定的参考。

3.4 地震周期对主动土压力的影响

对于拟动力法中的众多参数，地震波周期是其中较为重要的参数。为研究其对主动土压力的影响，通过计算得到当水平地震系数kh＝0.05～0.25时，主动土压力Pa随地震周期T变化的规律，如图6所示。

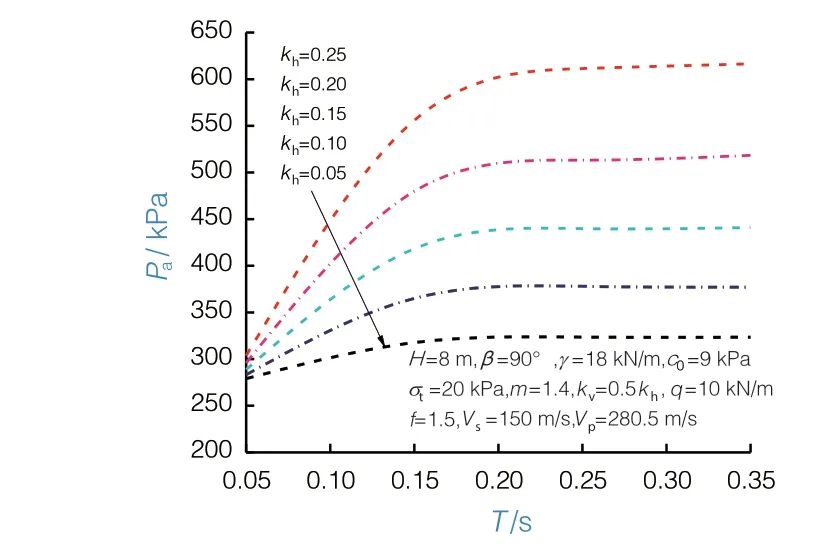
图6 地震波周期对主动土压力的影响

从图6可以看出，当地震波周期T＜0.20 s时，随着其数值的增大，主动土压力逐渐增大；而当T＞0.20 s后，随着地震波周期的增大，主动土压力趋于稳定。这是因为墙后填土的几何尺寸有限，当地震波周期增大到某一数值之后，地震波的波长远大于墙后填土的高度，因此在墙后填土范围可以视为地震加速度不再随所处高度而变化，若此时不考虑土体放大系数的影响，则拟动力法退回为拟静力法。这也可以看出拟动力法是能够包含拟静力法的，因此其适用性更广。

3.5 波速对主动土压力的影响

压缩波和剪切波的动态特性对主动土压力产生较大影响。如前所述，对于大多数土壤材料，当泊松比为0.3时，剪切波波速与压缩波波速之比为常数1.87。因此，在本文中只讨论了压缩波波速的影响。为研究其对主动土压力的影响，通过计算得到当水平地震系数kh＝0.05～0.25时，主动土压力Pa随压缩波波速Vs变化的规律，如图7所示。

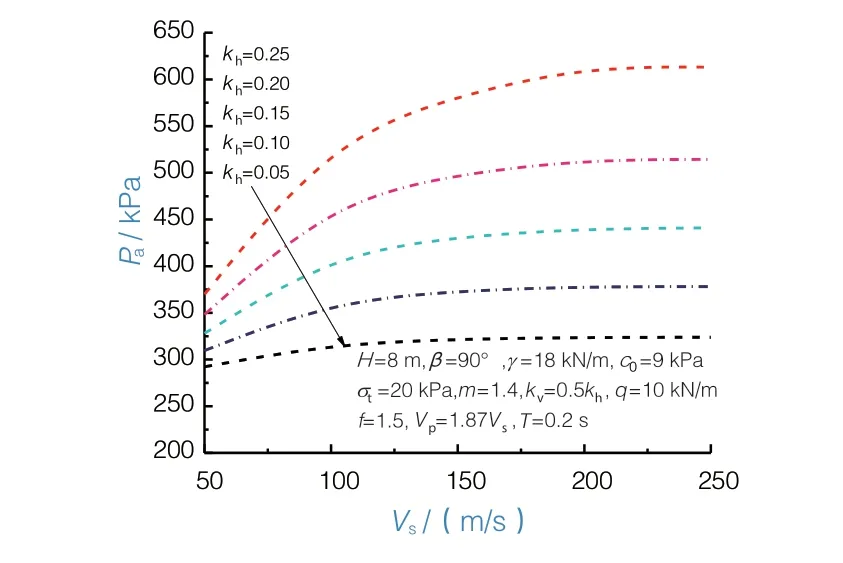
图7 压缩波波速对主动土压力的影响

从图7可以看出，刚开始随着压缩波波速的增大，主动土压力逐渐增大，之后便稳定为一数值基本保持不变。同样的，作为波长的另一个决定因素，当波速增大到某一数值之后，地震波的波长将远大于墙后填土的高度，因此在墙后填土范围可以视为地震加速度不再随所处高度而变化，其结果逐渐趋近于拟静力法得到的结果。

3.6 初始相位差对主动土压力的影响

当同时考虑压缩波与剪切波时，两者传递到墙后填土底部具备一定的时间差，在本文中称其为初始相位差。为研究其对主动土压力的影响，通过计算，得到当水平地震系数kh＝0.05～0.25时，主动土压力Pa随初始相位差t0变化的规律，如图8所示。

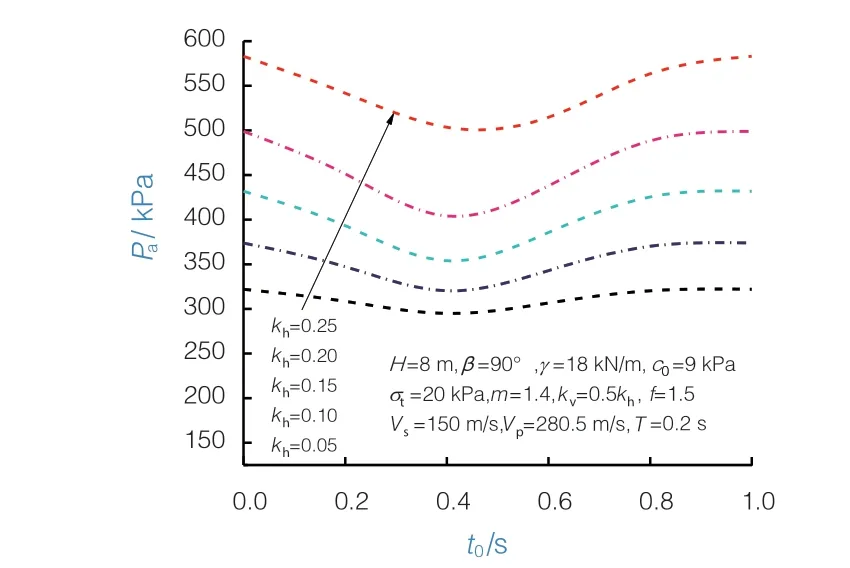
图8 初始相位差对主动土压力的影响

从图8可以看出，刚开始随着初始相位差的增大，主动土压力逐渐减小，之后便随着初始相位差的增大而增大。同时，当初始相位差t0＝0和t0＝T时，二者计算得到的主动土压力数值相同，也就表现出明显的周期性，这与我们采用的正弦分布形式的地震波相吻合。

3.7 土体放大系数对主动土压力的影响

对于随着地震波接近回填土表面，振动将被放大这一现象，引入了土体放大系数这一参数。为研究其对主动土压力的影响，通过计算得到当水平地震系数kh＝0.05～0.25时，主动土压力Pa随土体放大系数 f 变化的规律，如图9所示。

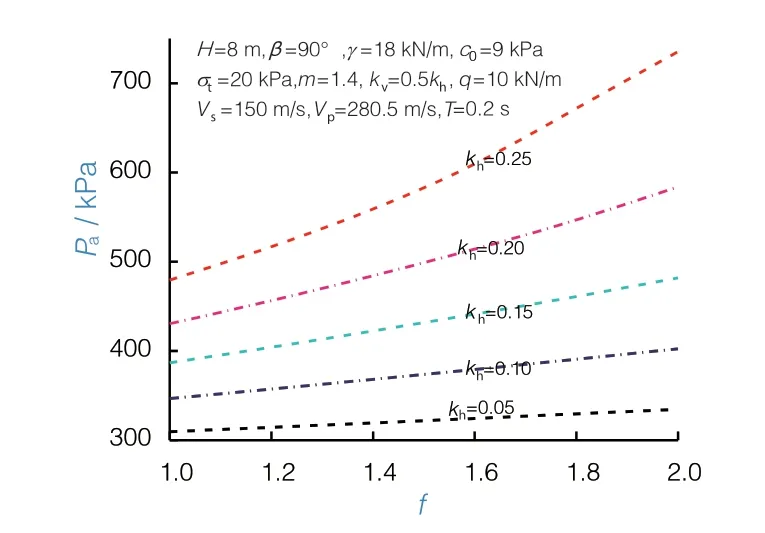
图9 土体放大系数对主动土压力的影响

从图9可以看出，随着土体放大系数的增大，主动土压力逐渐增大。对于kh＝0.05，当 f 从1.0增大到2.0，主动土压力的数值增大约1.08倍；而对于kh＝0.25，当 f 从1.0增大到2.0，主动土压力的数值增大约1.53倍。因此，在高水平地震加速度系数情况下，土体放大系数的影响更为显著，在实际工程中应该予以重视。

3.8 垂直地震系数对主动土压力的影响

在已有的一些研究中，均发现垂直地震系数对土工构筑物稳定性影响较小这一结论。本文也对其进行了研究。通过计算得到当水平地震系kh＝0.05～0.25时，主动土压力Pa随垂直地震系数kv与水平地震系数kh的比值μν变化的规律，如图10所示。

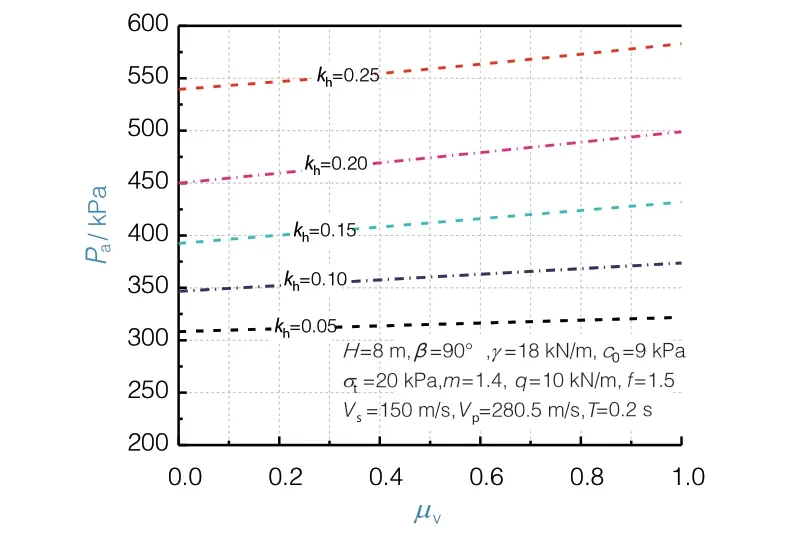
图10 垂直地震系数对主动土压力的影响

从图10可以看出，随着垂直地震系数的增大，主动土压力略微增大。在不同的水平地震系数条件下，μν＝1.0与μν＝0得到的主动土压力相差均不超过10%。因此与其他学者得到的结论一致，即垂直地震系数对土工构筑物的稳定性影响较小，在实际工程中，可以不考虑垂直地震系数的影响。

4 结语

本文研究的主要目的是基于塑性理论，建立一种用于计算在非线性条件下主动土压力的新方法。在对于考虑地震的效应中，以正弦形式的地震系数来计算惯性力，也就是拟动力法。在基于极限分析的上限定理，利用一种水平计算单元分别计算外力功率和内能耗散率并推导出了主动土压力的解析解。通过对计算结果进行分析，得出了以下结论：

1）线性条件下，即m＝1.0时，本文的计算结果与Chen等[15]的研究吻合良好，从而证明了所提出方法的正确性。

2）土体本身具备较强的非线性特征，采用非线性强度准则来描述其强度特性将得到更为精确的解析解。而对于非线性Mohr-Coulomb强度准则中的3个参数，其中初始黏聚力的增大有利于墙后填土的稳定，较大值将得到较小的主动土压力值。而非线性系数和单轴抗拉强度的增大均不利于墙后填土的稳定，较大值将得到较大的主动土压力值。

3）对于拟动力法相关参数，水平地震系数、地震波周期、压缩波波速、土体放大系数、垂直地震系数的增大均导致主动土压力的增大，而对于初始相位差则表现出明显的周期特征。