基于奇异谱和相关性分析的木材声发射源直线定位算法研究

丁 锐，罗蕊寒，赖 菲，王明华，邓婷婷，罗廷芳，李 明

(1.西南林业大学 机械与交通学院，云南 昆明 650224；2.安徽工程大学 电气工程学院，安徽 芜湖 241000)

声发射检测技术(acoustic emission test,AET)作为一种主动式的无损检测技术，已应用在金属、岩石、木材及复合材料的缺陷与损伤监测等领域[1-3]。木材作为一种典型的各向异性材料，在人们的生活中具有广泛的应用，实现木材损伤AE源定位是木质材料无损检测的研究热点之一。

受随机因素影响，实际AE信号中含有大量会对AE源定位精度产生显著影响的噪声信号，从噪声中析取AE信号是进行AE源定位的关键问题。近年来，在奇异值分解的基础上发展起来的SSA技术，不仅与信号模型独立，而且不受噪声的频谱分布的影响，已经广泛应用于信号的降噪处理中。文献[4-6]采用基于相空间重构和SSA的混沌信号自适应降噪方法，有效地从被噪声严重污染的观测数据中重构混沌信号。针对维纳滤波算法在处理非平稳语音信号噪声时信号失真的问题，文献[7]提出了一种SSA和维纳滤波相结合的语音去噪算法，不仅能有效地去除背景噪声，而且能保留原始信号的细节。文献[8]将基于SSA的方法用于滚动轴承故障诊断中，结果表明，SSA能够有效地从振动信号中提取轴承故障的信息特征，有助于提高轴承故障诊断的准确性。针对经验模式分解无法对信噪比较小的原始信号进行正确分解而失效的问题，文献[9]采用SSA和经验模式分解相结合的方法提取微弱特征信号。文献[10]针对提高信号的信噪比问题，通过SSA分解并重构测站大地高序列，确定嵌入维数的选择原则和被截断的主成分数。通过仿真试验，进一步采用SSA方法提取CORS时序形变信息。目前有关SSA的研究大多关注于语音处理、设备故障检测等方面，而在木质材料损伤检测中的研究相对较少。

本研究以樟子松(Pinussylvestrisvar.mongolica)和榉木(Zelkovaschneideriana)为试验材料，提出一种基于SSA和信号相关性分析的木材表面AE源直线定位算法。首先，利用SSA析取原始AE信号中的有效AE信号，然后利用信号相关性分析方法计算AE信号在两传感器之间的传播时差，并计算其传播速率。在此基础上，依据传感器与AE源的几何关系设计直线定位算法进行AE源定位。最后，通过对比分析SSA处理前后AE源的定位结果，进而验证SSA对提高木材表面AE源定位精度的积极作用。

1 材料与方法

1.1 材料

选择纹理通直的樟子松和榉木为试验材料，2种试件气干状态下的密度和绝对含水率分别为0.42 g·cm-3、12.8%和0.699 g·cm-3、14.3%，试件规格均为1 000 mm(长)×50 mm(宽)×15 mm(厚)。使用LabVIEW软件及NI USB-6366采集设备构建2通道的高速数据采集系统，选用2个SR 150N单端谐振式AE传感器，信号带宽为22～220 kHz，配置的前置放大器增益为40 dB，放大器输出的电压范围为(-5V，5V)。由文献[11]得知，木材AE信号的频率主要分布在50～200 kHz，根据香浓采样定理，为不失真地恢复模拟信号，采样频率fs和信号最大频率fmax之间应满足fs≥2fmax，故本研究设置500 kHz为每个AE信号采集通道的采样频率。

1.2 方法

由于木材在实际损伤和断裂的过程中有多个AE源产生，而本研究主要针对单个AE源的定位问题，所以通过折断铅芯的方式产生单个AE源。为保证所产生的每个AE信号的一致性，参照ASTM E976-2015标准，在试件表面以30°夹角、距离接触点2.5 mm的位置，通过折断0.5 mm铅笔芯的方法产生AE源。

AE源定位的前提是计算AE的传播速度，为此，专门设计了用于计算AE传播速度的试验(图1)。以试件长度的中心为原点，在试件长度方向建立一维坐标轴x，并规定传感器S1指向S2方向为正方向。在x=-250 mm和x=250 mm 2处分别放置传感器S1和S2，并在x=-300 mm处通过折铅的方式产生AE源，进而根据到达2个传感器的AE信号之间的时间差，计算AE信号在木材表面的传播速度。AE源定位采用同样的试验方法，具体而言，分别将传感器S1和S2放置到x=-300 mm、x=300 mm处，并分别在x=150 mm和x=200 mm处产生AE源，进一步依据所测得的AE信号传播速度进行AE源定位。

图1 试验方案示意Fig.1 Schematic diagram ofthe test scheme

1.3 SSA降噪算法

SSA是使用相空间重构来实现通过奇异值分解来识别原始信号分量(例如趋势，周期或准周期，噪声等)的目的[12]。SSA处理AE信号的核心思想是：将一维时间序列转换为多维度序列进行主成分分析，将有效AE信号成分进行分组处理，并根据累计贡献率选择若干分量进行重构[13]。SSA有2个阶段：分解和重构，分解阶段分为嵌入和奇异值分解(singularvaluedecomposition，SVD)，重构阶段分为分组和对角线平均，木材表面AE源信号进行SSA降噪处理的具体过程如下：

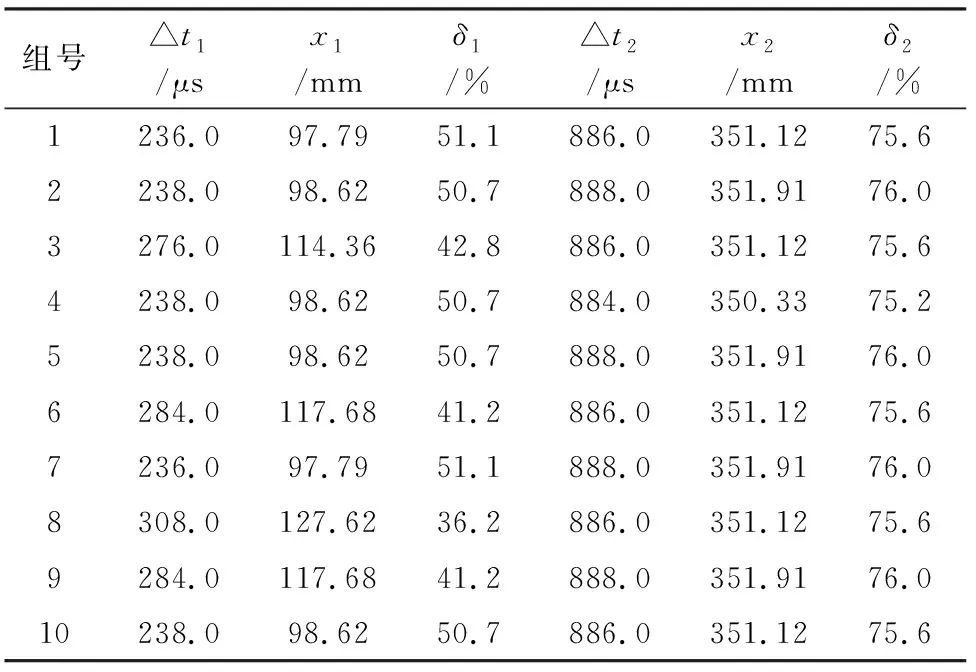
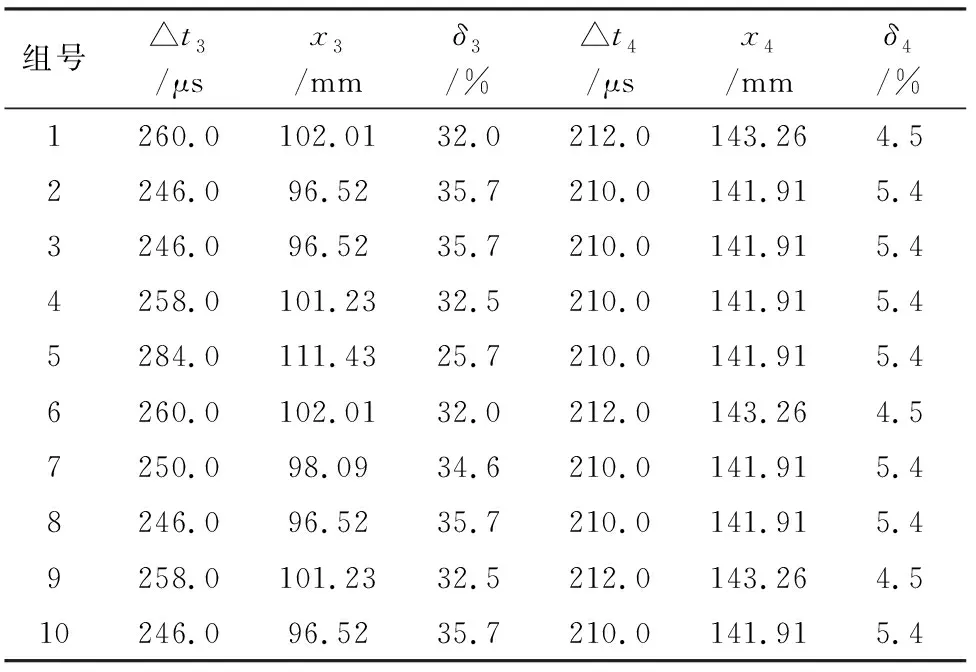
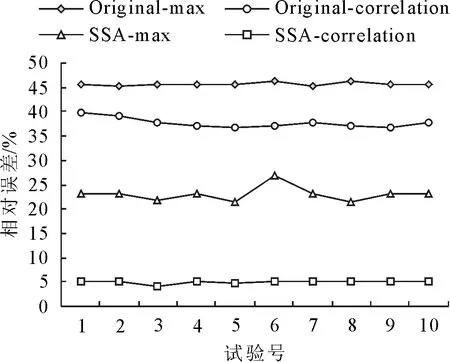
1.3.1 嵌入和奇异值分解 假设所采集到的AE源信号为XN=(x1,x2,…,xN)，其中N为时间序列长度，设窗口长度为L,L为整数且1

(1)

在嵌入的过程中，窗口长度L和K具有运算关系，即K=N-L+1。

将AE源信号XN映射为轨迹矩阵X后，对XXT进行奇异值分解，计算出矩阵XXT的非负特征值λ1，λ2，…，λi，以及对应的正交特征向量U1,U2,…,Ui，并将特征值按降序排列。设非零特征值的个数为d，Ui与Vi为轨迹矩阵X的左右特征向量，轨迹矩阵可由初等矩阵合成[14],则X可表示为:

(2)

1.3.2 分组与对角平均 为分离有用信号成分，选取式(2)中的前r个初等矩阵Xi近似为轨迹矩阵X，并将其分成p组，假设第Ij组内有jm个矩阵，然后将每组内的矩阵相加得到新的矩阵XIj，则X可以近似表示为:

(3)

对角平均是将矩阵还原为时间序列的方法，通过将上述公式分组和分解而获得的矩阵转换成所需长度N的序列。设Y是一个L×K的矩阵，其元素为yij，令L*=min{L,K}，K*=max{L,K}，且N=L+K-1，通过对角平均公式重构时间序列，将矩阵Y变换为长度为N的序列y1,y2,…,yN，如下为对角平均公式：

(4)

通过对角平均公式(4)即可将分组过程中所选取的前r个矩阵还原为时间序列。一般而言，在系统的奇异谱中，前面较大的奇异值则对应信号中的特征成分，而那些较小的奇异值就构成了所谓的噪声平台，反映了信号中的噪声成分。

1.3.3 SSA参数的选择 在以上SSA降噪的过程中，嵌入和分组需要进行参数的选择。在嵌入时，由于窗口长度L和K具有运算关系，即K=N-L+1，窗口长度为L和K的轨迹矩阵的奇异值分解是对称的，从轨迹矩阵中提取到的奇异谱相同，所以窗口长度≤N/2。而且，窗口长度L选择的越大，分解的序列越精细，但是L过大，反而会增加奇异值分解的时间[12]。同时，过小的L往往会造成序列中AE信号和噪声信号混杂在一起[15-16]。有学者研究了随窗口长度L变化的Hankel轨迹矩阵的奇异值[17]，并从理论上证明了当L取N的中值时，该奇异值达到最大值，同时也表明在大多数情况下L取N的中值是最佳的选择。所以，本研究选取窗口长度L=N/2，其中所采集的AE源信号的时间序列长度N=10 000。

在分组过程中，通过比较前r个子矩阵的累计贡献率η*和算法所设定的阈值η的大小，得到满足阈值的子矩阵个数，以此来确定选取的奇异值个数r。当累计贡献率η*>85%时，可认为所选取的前r个子矩阵包含了原始AE信号的大部分特征信息[18]，因此设定阈值0.85<η<0.9。

1.4 木材AE源定位

1.4.1 计算AE信号传播速度 试验中2个传感器定距离分布于试件表面，因此只需确定AE信号到达2个传感器的传播时差△t，进而便可通过公式v=△x/△t求得AE信号在木材表面的传播速度，分别采用最大值和相关性分析确定信号的传播时差。

最大值分析法是基于信号最大峰值在时间轴上的平移单位确定传播时差，假设AE信号到达2个传感器的时差为△t，则：

△t=△l/f

(5)

式中，△l表示AE信号从传感器S1传播至S2处时，信号峰值在时间轴上的平移单位；f为采样率。

采用信号相关性分析法确定传播时差△t时，互相关函数主要是描述2个信号的相似程度，信号x(t)和y(t)的互相关函数定义为：

(6)

由互相关函数的定义可知，若τ=τ0时，互相关函数的绝对值|Rxy(τ0)|取得最大值，则意味着信号y(t)沿时间轴平移τ0个单位后，与信号x(t)最相似。为此，通过互相关函数可以间接确定AE信号在2个传感器之间的传播时差。

1.4.2 直线定位算法 在图1中，将传感器S1和S2分别调整到x=-300 mm、x=300 mm处，并在x=150 mm和x=200 mm处分别采用铅芯折断的方式产生人工AE源。

由线性几何关系可知，AE源的位置可由下式确定：

(7)

式中，x为AE源的实际位置；v为AE信号在木材表面的传播速度；△t为AE信号到达2个传感器的时差。

2 结果与分析

不同算法用于计算AE信号的传播时差并以此计算AE信号在木材表面的传播速度会存在差异[19-21]。本研究采用4种不同的速度算法进行比较，针对不同的AE源位置，为减少试验随机性影响，分别进行10次独立试验。由于试验数据过多不能全部列出，且2种试件采用不同算法的定位效果类似，因此，以樟子松试件的定位结果为例说明不同算法的定位效果。表1和表2列出采用樟子松试件时4种不同算法所确定的AE信号传播速度的试验结果。其中，v1～v4分别是采用算法Original-max、Original-correlation、SSA-max、SSA-correlation所确定的速度。

表1 樟子松试件表面的AE信号传播速率Table 1 AEsignal propagation rate of P.sylvestris var.mongolica specimen surface (m·s-1)

由表1可知，4种不同算法所计算的速度有较大差异，比较v2和v4可知，对原始AE信号进行SSA降噪处理前后，两者速度平均值相差558.9 m·s-1，这是因为AE传感器所采集的原始AE信号中含有大量的噪声信号，受噪声信号的影响，直接通过信号相关性分析法并不能准确计算AE信号的传播时差。对比v3和v4可知，原始AE信号通过SSA预处理后，采用信号相关性分析和最大值分析所确定的AE信号传播速度的平均值在数值上相差了566.8 m·s-1。因此，采用算法SSA-max和算法SSA-correlation进行AE源定位，定位效果会存在较大差异。比较v1和v3可知，两者速度差异不大，由此可以说明最大值分析法并不能有效地识别AE信号，对噪声信号不敏感。

计算樟子松试件表面的AE信号的传播速度后，根据式(7)确定樟子松试件的AE源位置，其定位结果见表2～表5。直接使用原始AE信号进行定位的结果见表2和表3，表4和表5是通过SSA处理的AE信号定位的结果。

表2 原始AE信号在150 mm处的定位结果Table 2 Location results of original AE signal at 150 mm

表3 原始AE信号在200 mm处的定位结果Table 3 Location results of original AE signal at 200 mm

表4 AE信号经SSA处理后在150 mm处的定位结果Table 4 Localization results of AE signals at 150 mm after SSA processing

表5 AE信号经SSA处理后在200 mm处的定位结果Table 5 Localization results of AE signals at 200 mm after SSA processing

其中，时差△t1～△t4分别由算法Original-max、Original-correlation、SSA-max、SSA-correlation所确定，x1～x4分别为采用速度v1～v4时确定的AE源位置。在表中，δi(i=1,2,3,4)表示使用4种不同定位算法时的相对误差。

由表2和表3中的δ1和δ2可知，受原始AE信号中噪声的影响且信号相关性分析和最大值分析法不能识别有效的AE信号，未经SSA预处理直接对原始AE信号通过基于信号相关性分析或最大值分析方法计算AE信号的传播速度时，木材表面AE源定位的相对误差较大。

对比δ2与δ4可知，2个不同位置处相对误差的平均值之差分别为46.5%和73.1%，因此，在木材表面AE源直线定位中，对原始AE信号经SSA降噪处理析取有效的AE信号，进而通过信号相关性分析法确定AE信号的传播时差，定位精度显著提高。比较δ1和δ3可以看出，在对原始AE信号通过SSA降噪后，采用最大值分析法确定信号的传播时差，其定位精度提高不明显。

图2～图3和图4～图5分别为樟子松和榉木在150、200 mm处采用4种不同算法分别进行10次独立试验定位结果的相对误差，由此可知，在不同位置处，算法SSA-correlation的定位结果都比较稳定且相对误差较小，算法Original-correlation的定位结果的相对误差均较大，而算法Original-max和算法SSA-max在2个不同位置处的定位结果不稳定且误差较大。由式(7)可知，在传播速度v确定的条件下，时差△t的波动会导致定位结果的波动，所以采用最大值分析法确定AE信号的传播时差，会导致定位结果不稳定。这是因为2种时差计算方法都是从信号的时域角度进行分析，信号相关性分析法考虑的是全局的AE信号，最大值分析法则仅关注于AE信号中的峰值部分。而木材作为一种非均质的多孔材料，信号在传播过程中存在能量衰减、反射等现象，仅仅关注于信号的峰值并不能合理确定AE信号在木材中的传播时差。因此，对原始AE信号进行SSA降噪处理后，基于最大值分析法确定AE信号的传播时差，并不能实现对木材AE源的有效定位，而将原始AE信号通过SSA降噪处理后，采用信号相关性分析法确定信号的传播时差，能够有效提高木材表面AE源的定位精度。

图2 150 mm处樟子松试件定位结果的相对误差Fig.2 Relative error of positioning results of P.sylvestris var.mongolica specimen at 150 mm

图3 200 mm处樟子松试件定位结果的相对误差Fig.3 Relative error of positioning results of P.sylvestris var.mongolica specimen at 200 mm

图4 150 mm处榉木试件定位结果的相对误差Fig.4 Relative error of positioning results of Z.schneideriana specimen at 150 mm

图5 200 mm处榉木试件定位结果的相对误差Fig.5 Relative error of positioning results of Z.schneideriana specimen at 200 mm

3 结论与讨论

受木材构造、试验环境等随机因素的影响，原始AE信号中含有大量的噪声信号，本研究采用SSA对原始AE信号进行降噪预处理。结果表明，对原始AE信号进行SSA预处理前后，基于最大值分析法计算AE信号的传播速度时，在x=150 mm和x=200 mm处,樟子松试件定位结果的相对误差分别为55.7%、33.2%和46.6%、31.7%；榉木试件定位结果的相对误差分别为44.8%、54.9%和45.5%、22.9%。可以看出SSA预处理后定位精度没有明显提高，相对误差仍然较大。而基于信号相关性分析法确定信号传播速度时，对原始AE信号进行SSA预处理前后，在x=150 mm和x=200 mm处，樟子松试件定位结果的相对误差分别为51.8%、5.1%和75.7%、2.6%；榉木试件定位结果的相对误差分别为52.0%、3.1%和37.7%、5.1%，SSA预处理后定位精度明显提高且相对误差较小。因此，在木材表面AE源的直线定位中，对原始AE信号进行SSA降噪处理后，再基于信号相关性分析方法确定信号传播速度，能够明显提高木材AE源直线定位算法精度。

目前关于SSA在木材AE源定位方面的研究较少，本研究基于SSA和信号相关性分析的木材AE源直线定位算法，为研究木材AE信号的降噪处理和木材AE源的定位提供了一种方法和思路。未来可以将SSA算法进行改进，并与信号相关性分析方法相结合，应用于木材AE源平面定位的研究中，进一步提高木材AE源定位精度。