立木胸径近真值测量与计算模型的研究

郑似青,熊 伟,方陆明*,孙林豪,袁方星,郑辛煜

(1.浙江农林大学 信息工程学院，浙江 杭州 311300；2.浙江省林业智能监测与信息技术研究重点实验室，浙江 杭州 311300；3.浙江省龙泉市林业局，浙江 丽水 323700；4.国家林业与草原局林业感知技术与智能装备重点实验室，浙江 杭州 311300)

立木的直接测量因子及其派生的因子称为基本测树因子[1-2]，胸径作为直接测量因子之一与冠幅、材积有着高度的相关性，并可用于估算立木的蓄积量、生物量等指标，也是评价立地质量与林木生长状况的重要依据[3]，立木测定工具及其计算模型是获取基本测树因子的基本途径[4]，因此探索立木胸径的精准测量计算模型有现实意义。目前，主要测量工具是围尺和卡尺[5-6]，二者在适用范围和测量方法上存在一定差异性[7-8]。

近年来，出现了一些新兴的胸径测量方法或技术：例如无人机遥感影像[9-11]、RD1000电子测树仪[12]、电子经纬仪[13]、超站仪[14]、地面激光扫描(Terrestrial laser scanning)[15-18]、近景摄影测量(Close-Range Photogrammetry)[19-20]和带有TOF(Time of Flight)摄像头的智能手机[21-24]等多种非接触测量技术与方法，但在实际应用中仍存在测量精度不高，或携带不便或数据处理复杂费时等诸多问题，且它们通常将树干截面当作标准圆模型来提取胸径，系统性的单立木胸径偏差会产生林分或区域蓄积量、生物量等指标的大偏差。通常“直径”一词意味着立木的胸高断面是标准圆形。然而，相关研究证明[25]，立木不同方向的直径生长速度有差异，标准的圆形是极其罕见的，胸高断面更像是一个封闭的凸体，椭圆形或超椭圆形更能精准地体现树干和年轮的外形和生长情况[26-27]，但需切开树干作为研究材料，且估算超椭圆参数的方法复杂，也不便于开展大规模的森林资源调查工作。立木蓄积与胸高断面积密切相关，传统的胸高断面积都以单一的胸高直径作为标准圆模型来估算，胸径取值的不同或者使用椭圆模型、超椭圆模型对胸高断面的面积估算的影响也非常值得探索。

为在传统的胸径测量工具基础上探索更优的胸径测量方法、寻找更好的胸高断面积计算模型，本研究选取8个树种为对象，使用自制电子卡尺交叉测量每株立木1.3 m处的东西向胸径、南北向胸径、近似最大胸径、近似最小胸径，使用传统围尺测量对应胸高断面处周长作为参考值，以比较立木不同方向上胸径大小的差异性以及不同的胸高断面积计算模型的优劣。

1 材料与方法

1.1 试验地点及对象

临安区位于杭州市西部(29°56′-30°23′N，118°51′-119°52′E)，属亚热带季风气候，雨量充沛，年平均降水量1 613.90 mm，全年平均气温16.4℃，全年日照时数1 847.3 h。试验地点位于临安区浙江农林大学植物园(30°15′N，119°43′E)，以人工林为对象，选取银杏S1(Ginkgobiloba)、广玉兰S2(Magnoliagrandiflora)、梧桐S3(Platanusorientalis)、水杉S4(Metasequoiaglyptostroboides)、白玉兰S5(Magnoliadenudata)、樟树S6(Cinnamomumcamphora)、无患子S7(Sapindusmukorossi)、鹅掌楸S8(Liriodendronchinensis)等8个树种，共计245株，分别测量东西向胸径、南北向胸径、近似最大胸径、近似最小胸径以及胸高断面处的周长。

1.2 测量手段

使用传统围尺、电子卡尺2种测量工具。电子卡尺为浙江农林大学智能装备实验室自制，其构造与传统卡尺相似，具有抗干扰性强、高精度、操作简便、自动记数等优点[28]。首先将电子卡尺嵌套于树干，其次通过装置上的超声波传感器获得树干1.3 m左右位置处，然后保证尺身与两脚同时与树干断面接触时按下记录键，便可自动存储该树的胸径值，根据指南针依次测量不同朝向的树木胸径，最后通过PC端的上位机软件提取装置上的数据，其作业见图1-a；传统围尺使用太平洋牌京制钢围尺(量程:0～63.7 cm)，其作业见图1-b。

图1 测量作业Fig.1 Measurement diagram

1.3 测量与评估方法

使用传统围尺测量得周长为C，通过人工录入围尺测量数据；使用电子卡尺测量的每株立木东西方向上的胸径记为dew，南北方向上的胸径记为dns，近似最大胸径记为dmax、近似最小胸径记为dmin(图2)。测量结束后，通过蓝牙将电子卡尺中的测量数据上传至PC端并进行后续的评估。

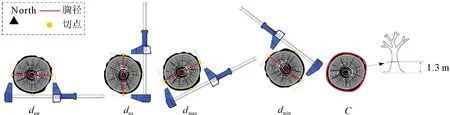
图2 测量方法Fig.2 The methods of measurement

1.3.1 差异性评估 树木在东西方向胸径和南北方向胸径的差异性主要采用p、E和Er3个指标进行评估，p为dew>dns的数量占总数的比例；E为胸径差，同时求其平均数和标准差；Er为径胸差的绝对值，同时求其平均数和标准差，相应公式如(1)、(2)。

1.3.2 圆曲线测量模型的评估 以dr=C/π作为直径参考值，平均值dm=(dns+dew)/2，对dew、dns、dm、dmax的准确性使用偏差(BIAS)、相对偏差率(relBIAS)、均方根误差(RMSE)和相对均方根误差率(relRMSE)进行评估，相应公式如(3)、(4)、(5)、(6)。其评估结果可以分别反映以dew为直径的标准圆模型Cew、dns为直径的标准圆模型Cns、dmax为直径的标准圆模型Cmax与以dr为直径的标准圆模型的接近程度。

E=dew-dns

(1)

Er=|dew-dns|

(2)

(3)

(4)

(5)

(6)

注：式(3)、(4)、(5)、(6)中xi为相对应的dew、dns、dm、dmax，xir为相对应的dr。

1.3.3 椭圆曲线测量模型的评估 对同种树木进行以dew和dns为长短轴的椭圆模型H评估：

1)使用式(7)计算离心率ec，并求其平均数和标准差；反映该种树木的树干截面扁平程度。

2)使用式(8)得椭圆周长L，围尺周长C作为参考值，使用平均偏差(BIAS)、相对平均偏差率(relBIAS)、均方根误差(RMSE)和相对均方根误差率(relRMSE)等指标进行评估。通过评估椭圆周长L与树干外围周长真值的接近程度来反映椭圆模型与实际树干截面的接近程度。

(7)

(8)

式中，a为dew和dns两者中较大值的1/2值，b为dew和dns两者中较小值的1/2值。

1.3.4 超椭圆的n参数估算和测量模型的评估 超椭圆曲线方程见式(9)，方程的特性曲线见图3。研究表明[20]，超椭圆模型的n参数为1.7～2.3，参考该取值范围得出的方法为：若某树种树干外围周长真值比椭圆模型所得的平均周长要大，则这种树木的胸围曲线更接近于n>2的超椭圆曲线，可选用评估区间为n=2+0.1k(k=1，2，3)；反之选用n=2-0.1k(k=1，2，3)。将n代入式(10)中得

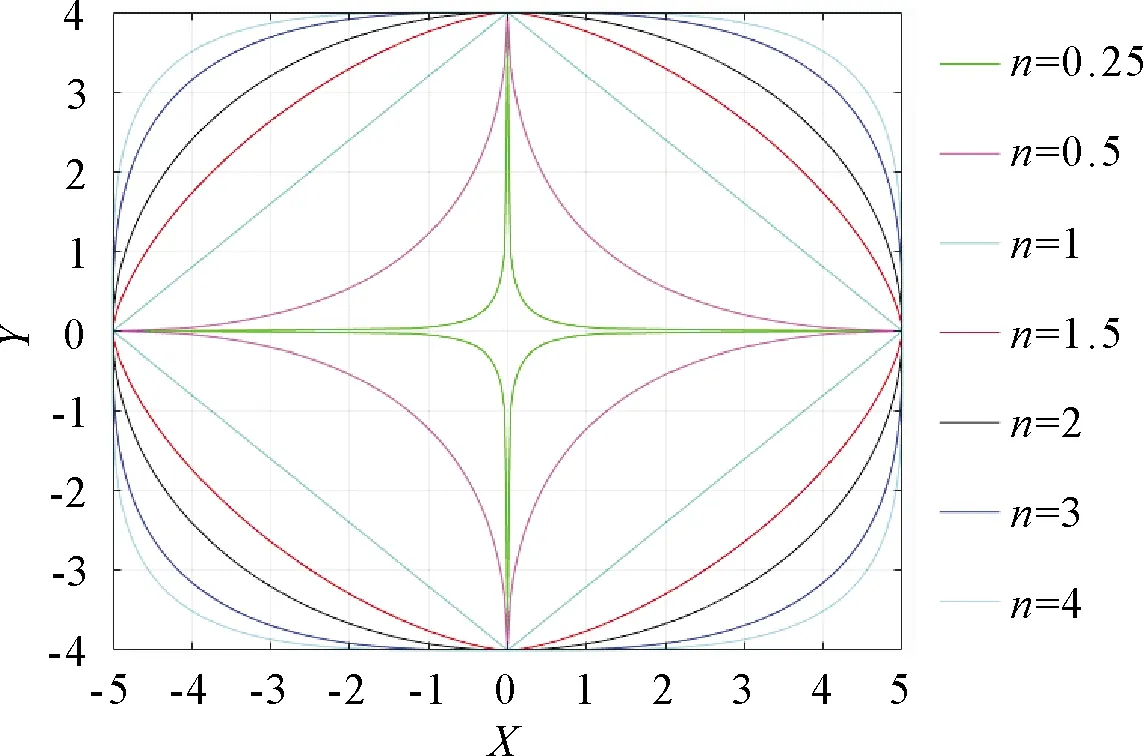
注：图3中a=5，b=4。图3 超椭圆曲线方程Fig.3 Super elliptic curve equation

到超椭圆曲线的周长S，再以围尺周长C作为参考值，使用式(1)计算评估区间内不同树种的平均偏差BIAS，找出该种树木的BIAS最接近0的值，并用na记下该nk的值。通过评估超椭圆周长S与树干外围周长真值的接近程度来反映超椭圆模型与实际树干截面的接近程度。

(9)

(10)

1.3.5 各模型胸高断面积估算 计算各个树种使用Cns模型、Cew模型、Cmax模型、H模型、SH模型和R模型所估算的面积，对应为：ACns、ACew、ACmax、AH、ASH和AR；用以评估不同的胸径取值或不同模型对胸高断面积估算的影响，模型具体信息见表1。其中，H模型、SH模型分别使用式(11)、(12)计算面积。

表1 各模型基本信息Table 1 The Basic information of models

AH=πab

(11)

(12)

式中，a为dew和dns两者中较大值的1/2值，b为dew和dns两者中较小值的的1/2值。

2 结果与分析

2.1 不同方向胸径差异性的评价结果

8个树种的p、E、Er的评价结果见表2，为探究树木最大胸径与最小胸径的方向分布规律，将胸径方向范围划分为A1 (0°～22.5°,337.5°～360°,157.5°～202.5°)、A2 (22.5°～67.5°,202.5°～247.5°)、A3 (67.5°～112.5°,247.5°～292.5°)、A4 (112.5°～157.5°,292.5°～337.5°)4组。8个树种近似最大胸径分布在A1～A4组的比例依次为18.78%、24.08%、37.55%、19.59%，8个树种近似最小胸径分布在A1～A4组的比例依次为31.84%、26.12%、21.22%、20.82%。

表2 p、E、Er的评价结果Table 2 Evaluation results of p,E,and Er

2.2 标准圆模型的评价结果

8个树种的dew、dns、dm、dmax评价结果见表3，与参考值dr的线性关系见图4，与参考值dr间差值分布见图5。

表3 dew、dns、dm、dmax的评价结果Table 3 The evaluation results of dew,dns,dm and dmax

图4 线性关系Fig.4 Linear relationship

图5 dew、dns、dm、dmax与dr误差分布Fig.5 Error distribution of dew,dns,dm,dmax and dr

2.3 椭圆模型的评价结果

8个树种的ec、L评价结果见表4，L与参考值C之间线性度对比见图6-a，差值分布见图6-b。

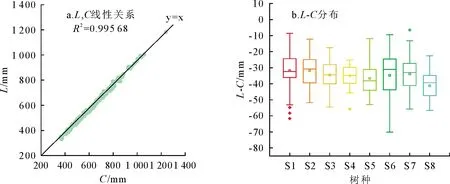
图6 L-C评价结果Fig.6 Evaluation result of L-C

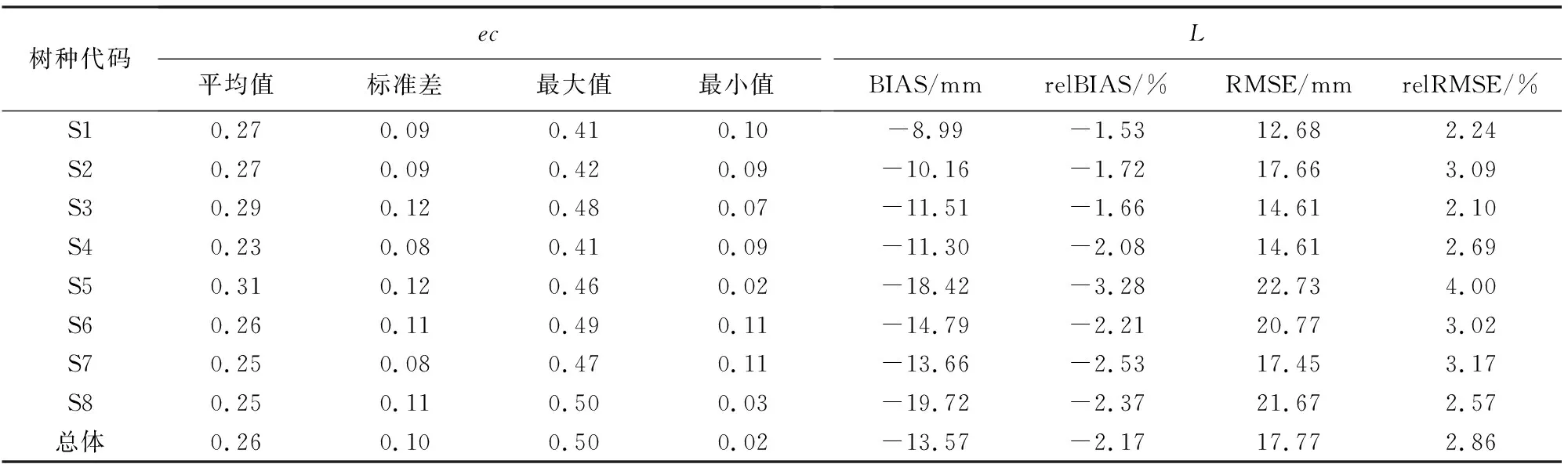
表4 ec、L的评价结果Table 4 The evaluation results of ec and L

2.4 超椭圆模型的评价结果

8个树种所估算得出最优n参数后超椭圆周长S的评价结果见表5。

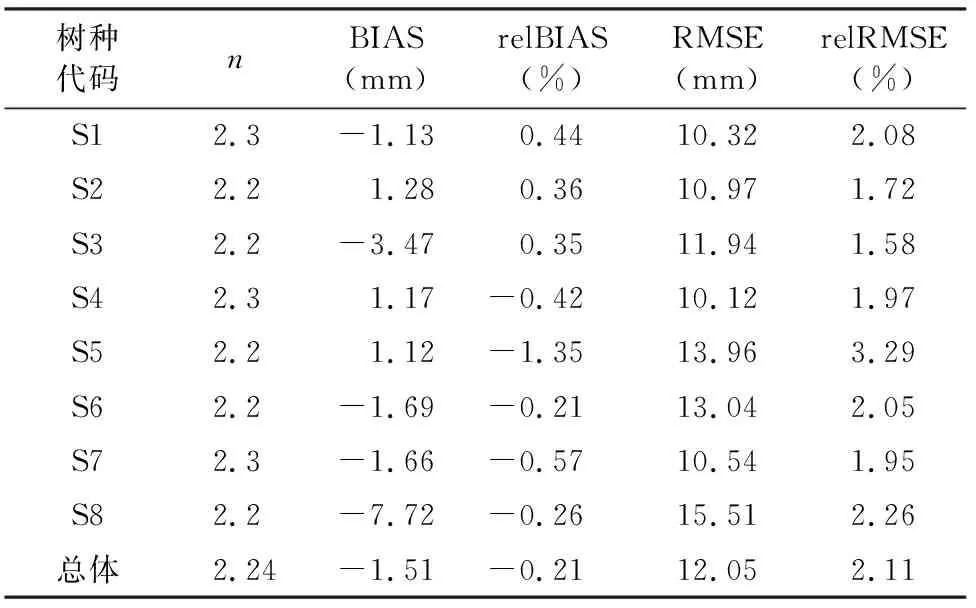
表5 S的评价结果Table 5 The evaluation results of S

2.5 各个模型胸高断面积估算结果

8个树种所使用的模型基本信息见表1，所估算的平均面积以及与R模型的比值见表6，各模型所估算面积对比见图7。

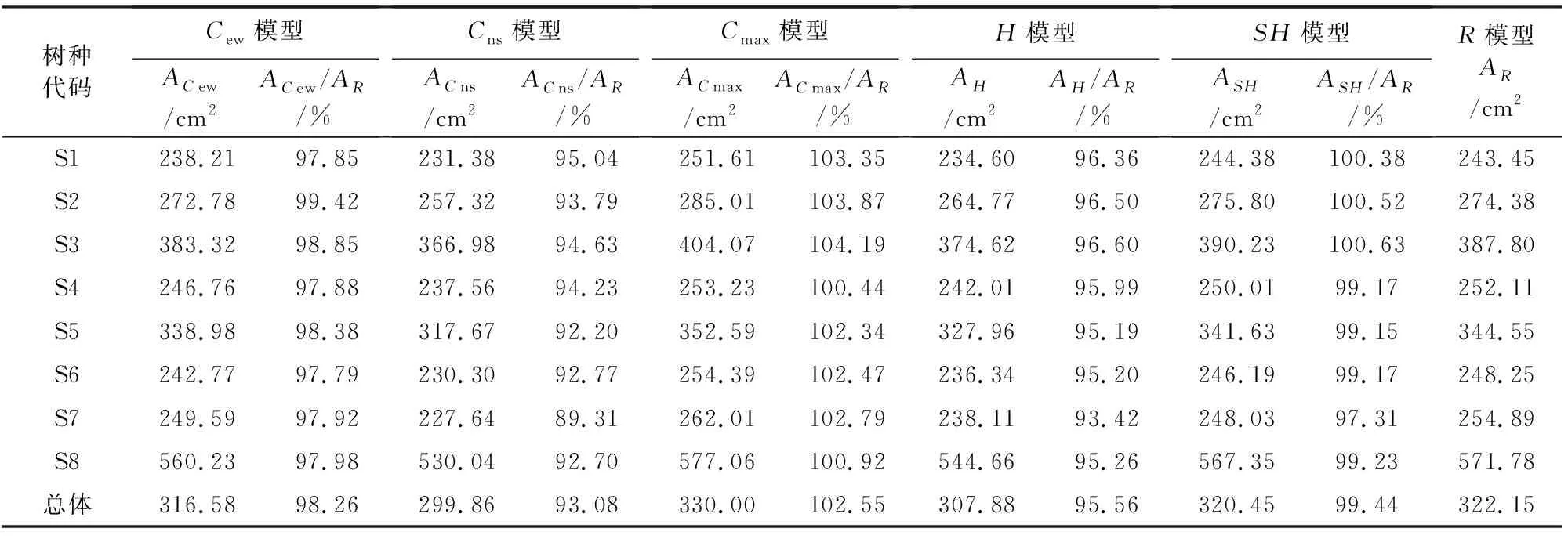
表6 各模型胸高断面积估算Table 6 The Estimation of cross-sectional area of breast height of each model

图7 各模型胸高断面积对比Fig.7 The comparison of cross-sectional area of breast height of each model

3 结论与讨论

立木东西向胸径比南北向胸径生长快的概率更高；对比不同方向上胸高断面积估算结果，Cew模型所估面积平均偏差为1.74%、Cns模型所估面积平均偏差为6.92%，因此实际测量中，对于卡尺单株单次测量时选择东西方向的胸径，估算的胸高断面积更准确。

基于椭圆模型，8个树种的平均离心率为0.26，一定程度上反映了其树干截面扁平程度；椭圆周长L与围尺周长C相比，其总体测量的偏差(BIAS)为-13.57 mm (-2.17%)，均方根误差(RMSE)为17.77 mm (2.86%)，可为寻找超椭圆参数提供参考。基于超椭圆模型，本研究所估算的最优n参数均值为2.24，所用方法简单，无需横切树干。在得出每种树木的n参数后，超椭圆周长S与围尺周长C相比，其总体测量的偏差(BIAS)为-1.51 mm (-0.21%)，均方根误差(RMSE)为12.05 (2.11%)。超椭圆模型相比于标准圆、椭圆模型估算胸高断面积更加准确。超椭圆(SH)模型所估面积为平均偏差为0.56%，Cew模型所估面积平均偏差为1.74%，椭圆(H)模型所估面积平均偏差为4.44%，Cns模型所估面积平均偏差为6.92%，且上述模型都低估了胸高断面积；6个模型中，仅Cmax模型高估了胸高断面积，平均偏差为2.55%。

从生态学角度，目前已经提出了各种因素对于树木截面的形状、螺旋纹和径向生长造成影响的假设，例如阳光照射、遗传因子、地球旋转、树液在树根和树冠的流动方式等[29]，具体如何影响还需深入研究。

虽然唐守正[30]较早地从理论上证明，不计测量误差时卡尺多个方向测径平均值趋向(接近)围尺测径值，但实际试验表明，相比围尺，卡尺测量胸径结果平均偏小2%左右，推测可能是围尺测量难以保证尺面在同一平面，致使围尺测量结果偏大。若考虑树皮厚薄引起的具体计算误差，需切开树干进一步研究，理论上树皮越厚误差越大。