基于改进GWO算法的永磁同步电机滑模MRAS控制
2021-10-14王泽霖胡启国
王泽霖,胡启国
(重庆交通大学 机电与车辆工程学院,重庆 400074,中国)
永磁同步电机(permanent magnet synchronous motor,PMSM)因具有效率高、功率密度大、转矩脉动小、体积小等优点,已被广泛的应用于航空航天、机器人、轨道交通及电动汽车等领域[1-2]。传统的PMSM通常采用高精度、高分辨率的速度和位置传感器如旋转变压器、光电编码器等来检测转子转速和位置角信息,但高性能的传感器不仅提高了电机成本,且易占用空间并给电机的安装带来了不便,因此无传感器控制技术在近些年来受到关注[3]。
无传感器控制的方法主要分为2种:一种是用来检测电机在零低速运行时的转子速度和位置角,如高频电压信号注入法、高频电流信号注入法等;另一种是用来检测电机在中高速运行时的转子速度和位置角,如模型参考自适应系统(model reference adaptive system,MRAS)法、扩展Kalman滤波器法、滑模观测器法等[4-5]。
MRAS是从20世纪50年代后期发展起来的一种自适应控制系统,于 1989年被用于估计异步电机的转速和PMSM[6]。该方法算法简单、收敛速度快[7-10]。
滑模MRAS(sliding model MRAS)是在MRAS基础上引入滑模变结构控制而来,以提高MRAS的鲁棒性和抗扰性,但由于较大的系统抖振以及较大的观测误差值,又有改进:文献[11]采用饱和函数来替换传统滑模MRAS中的开关函数,使系统运行更加平稳;文献[12]用一种边界层可变的新型饱和函数替换传统滑模MRAS中的开关函数,使系统拥有良好的转速估计效果;文献[13]采用一种连续切换函数Sigmoid取代了传统滑模MRAS的开关函数,有效地平滑了控制信号;文献[14]构造了边界层可变的正弦饱和函数来替换传统滑模MRAS的开关函数,抑制了滑模控制产生的抖振。
文献[11-14]均通过变换开关函数的方式来改善滑模MRAS的性能,但开关函数并不是唯一的影响因素,滑模控制部分所使用的积分滑模面同样会对系统的收敛速度及精度产生一定影响,进而影响系统的动态特性。
灰狼优化(grey wolf optimizer,GWO)算法是2014年由Mirjalili等提出的一种仿生智能算法,具有计算量小、结构简单、易编程实现等特点[15-16],近年来,被普遍应用于电力系统控制、飞行器轨迹规划等领域。
本文引入了非奇异快速终端滑模面[17]与积分滑模面相融合,构成积分型非奇异快速终端滑模面,以使系统的收敛性得到进一步增强;用非线性指数函数代替传统滑模MRAS中的开关函数,来削弱抖振;利用改进的灰狼优化(GWO)算法,对滑模面参数进行寻优整定。以仿真结果来证实该方案的可行性。
1 PMSM数学模型
与内置式PMSM相比,表贴式PMSM转动惯量小、电流响应快且其制造成本低。本文以表贴式PMSM为研究对象,采用d轴定子电流id= 0的转速电流双闭环矢量控制策略。PMSM数学模型包括定子电压方程、磁链方程、电磁转矩方程以及转子运动方程。本文内容仅涉及PMSM的定子电压,只建立定子电压方程的数学模型。
忽略电机的磁滞损耗及定子铁芯饱和等问题,建立PMSM的定子电压方程如下:
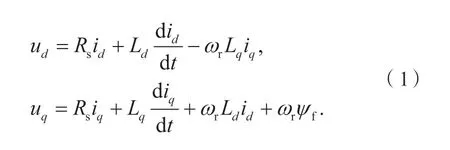
式中:ud、uq与id、iq分别为d-q轴坐标系即两相旋转坐标系下的定子电压与电流;Rs为定子相电阻;Ld、Lq分别为d-q轴坐标系下的电感,且Ld=Lq=Ls;ωr为转子角速度;ψf为永磁体磁链。
2 新型滑模MRAS设计
2.1 MRAS理论
MRAS包含了3部分即参考模型、可调模型与自适应律,其中自适应律的设计最为关键,通常采用以超稳定与正性动态系统理论为基础的设计方法来设计自适应律。
将式(1)整理后可得参考模型为:

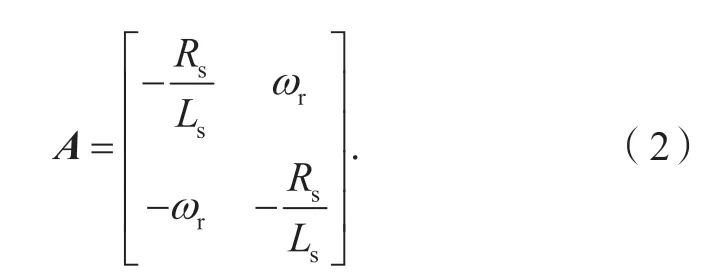
将式(2)以估计值表示,有可调模型为:
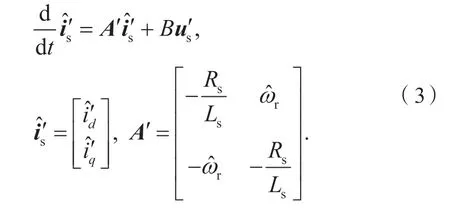
将式(2)与式(3)相减,可得定子电流矢量误差方程:
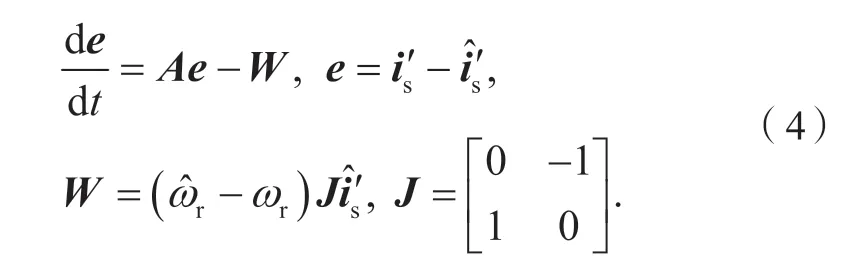
式中:e为定子电流广义误差。
由式(4)再结合Popov 超稳定理论,对Popov积分不等式进行逆向求解,即可得到自适应律,最后求得的转速自适应律为
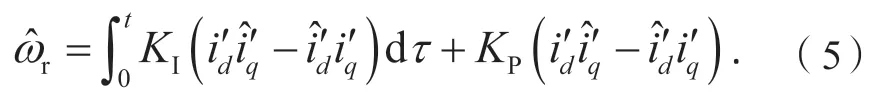
2.2 滑模MRAS理论
传统MRAS的转速自适应律存在着恒定的比例积分(proportional integral,PI)参数,当产生负载扰动等外界干扰时,会显著影响转速的观测精度。为此,相关学者将滑模控制引入MRAS并用其设计自适应律,形成滑模MRAS。滑模控制是利用系统的误差值来设计控制机构,且系统状态参数最终均会稳定在滑模面上,因而具有一定的鲁棒性。
滑模MRAS自适应律主要包含滑模面的设计与转速观测器的设计。
选择将MRAS的转速自适应律即式(5)作为滑模面s:

设计转速观测器为
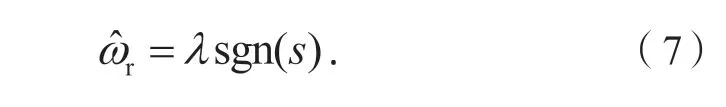
式中:λ为观测器增益,且λ>0;sgn为开关函数。
2.3 滑模MRAS改进
传统积分滑模面会使系统产生较高的超调量以及较长的调节时间,会降低系统的收敛性能;因而在此引入非奇异快速终端滑模面,该滑模面具有轨迹跟踪速度快、收敛精度高等特点,其表达式如下:

式中:x1为系统状态变量;α、β∈R+;p、q、g、h∈N,且1<p/q<2,g/h>p/q。
现将非奇异快速终端滑模面(即式(8))与传统积分滑模面(即式(6))相结合,构成积分型非奇异快速终端滑模面,其设计如下:
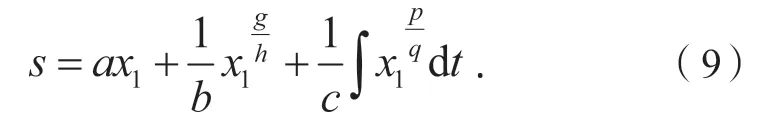
式中:a,b,c∈R+。
式(9)中所设计的滑模面同时融入了积分模块与非奇异快速终端模块,既保留了原积分滑模面的强鲁棒性又纳入了非奇异快速终端滑模面的快速收敛特性。
为改善系统抖振现象,得到良好的转速观测值,将式(7)中的开关函数替换为一种非线性指数函数,再结合式(9),构成新的转速观测器如下:
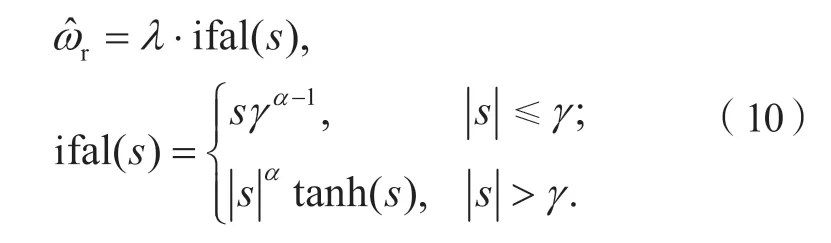
式中:ifal(·)是在原fal函数基础上将开关函数sgn替换为双曲正切函数tanh以进一步优化整体的控制性能。
为保证新转速观测器即式(10)的稳定性,构造Lyapunov函数如下:

结合式(2)、(9),x1可写为
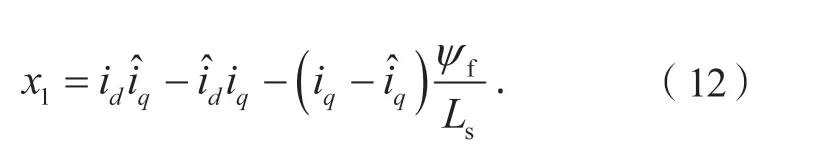
对式(12)两端求导后可得:
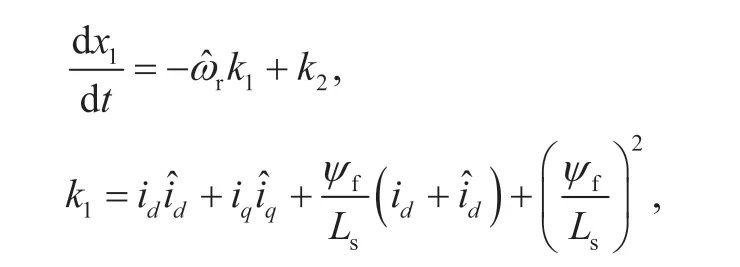

对式(11)两端求导并结合式(9)、(12)与 (13),得
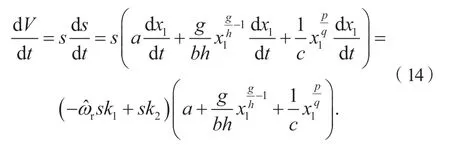
依据Lyapunov稳定性判据,要使观测器稳定,则需满足(dV/dt) ≤0,根据式(14)可最终推导出当式(10)中的λ足够大时,此时式(10)可满足稳定性条件。
根据所设计的转速观测器,可得出转子位置观测值为

由上述可知:原MRAS、滑模MRAS与新型滑模MRAS之间的差异仅体现在自适应律方面,参考模型与可调模型均一致,且分别如式(2)、(3)所示,其各自的自适应律汇总于下表1。

表1 自适应律结构对比
3 改进GWO算法设计
3.1 GWO算法理论
在灰狼群体中可以分为α狼、β狼、δ狼和ω狼4个等级,其中α、β、δ狼为群体中的领导狼,主要负责引导其余狼即ω狼来狩猎,其数量通常各设为1且将三者的位置分别作为算法的最优解、次优解和第三优解,ω狼的数量通常为几十以上且将它们的位置作为算法的候选解。在每一次迭代中,通过适应度函数计算出每只灰狼所在位置的适应度值,来评价各灰狼位置的优劣,并同步更新α、β、δ及ω狼的位置,最后,将α狼的位置输出即可得出每次迭代中算法的最优解。灰狼群体的捕猎行为分为包围、追捕和攻击3个阶段。
包围阶段的数学表达式为:
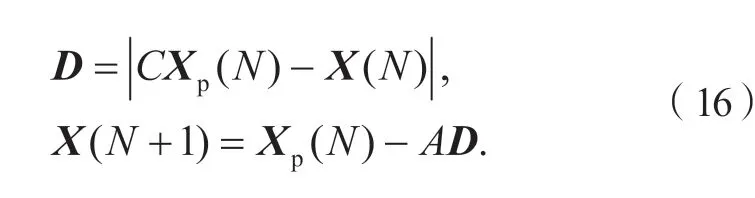
式中:D为灰狼与猎物之间的距离向量;Xp(t)与X(t)分别为猎物与灰狼的当前位置向量;N为当前迭代次数;A和C为系数且定义如下:
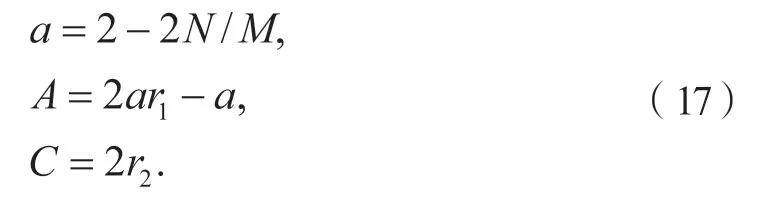
式中:M为最大迭代次数;r1、r2为区间[0,1]内的随机值。
追捕阶段的数学模型可表达为
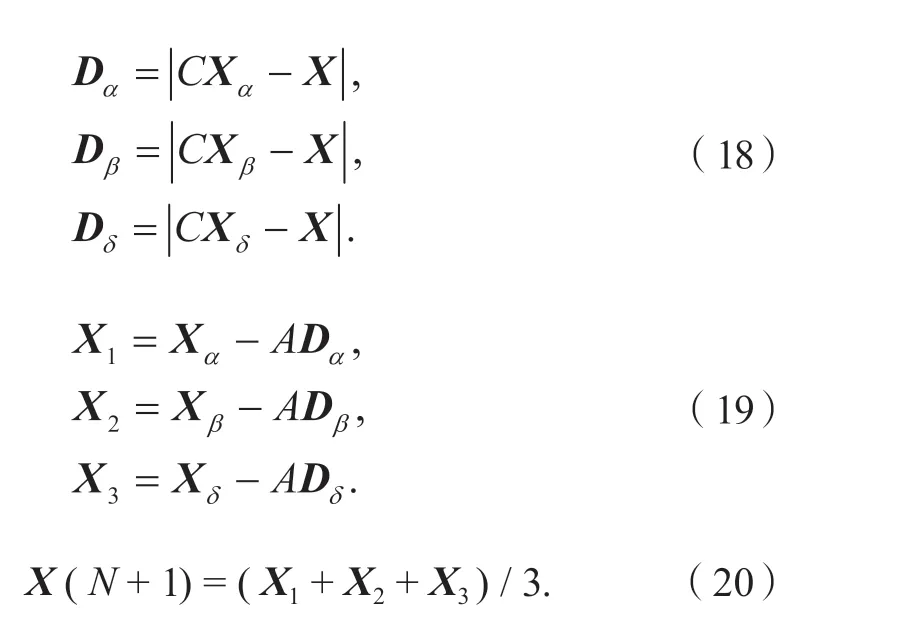
式中:Dα、Dβ、Dδ分别为α、β、δ狼与其余狼之间的距离向量;Xα、Xβ、Xδ分别为α、β、δ狼的当前位置向量;X为其余狼的当前位置向量。
在攻击阶段,由式(17)知,随着迭代次数N逐渐从0升至M,a由2逐渐降至0,且A为区间[-a,a]内的随机值,并当|A|≤1时,狼群在某一区域对猎物进行攻击,突出局部搜索;当|A|>1时,狼群分散搜捕猎物,突出全局搜索。
3.2 GWO算法改进
由式(17)可得:随着迭代次数N逐渐从0增至M,A的随机取值区间由[-2,2]逐渐向中心对称缩减为0。无论是在迭代前期还是在迭代后期,A值随机落在区间[-1,1]内的概率都将大于落在,余区间的概率,从而,灰狼群体在整个捕猎过程中,局部搜索所占的比重大于全局搜索,此情况极有可能导致算法陷入局部最优解,以及出现过早收敛等现象。因此,合理的方案应为:在迭代前期,全局搜索占主导地位;在迭代后期,局部搜索占主导地位,即要求A值在迭代前期随机落在区间[-1,1]内的概率小于落在其余区间的概率,在迭代后期反之。最后,依照要求,对A值赋予的新算法为:

式(21) 可得:在整个迭代过程中A值随机落在区间[-1,1]内的概率逐渐从0增至1,而落在其余区间的概率反之,即表明全局搜索的比重逐渐减小,而局部搜索的比重逐渐增大。此方法满足了算法要求,可有效地改善算法性能。
3.3 改进GWO算法验证
为验证改进后GWO算法的可行性,选取某一二阶延迟系统作为被控对象(其传递函数如式(23)所示),利用PI控制方法对其进行闭环控制,采用一水平阶跃作为控制系统的给定值。其中,PI参数分别采用改进前的与改进后的GWO算法来进行整定。步骤如下:
步骤1:设置算法相关参数,包括种群规模S、最大迭代次数M等;
步骤2:对灰狼群体位置进行初始化;
步骤3:计算所有灰狼个体的适应度值,并排序,将排名前3的灰狼个体位置分别记为Xα、Xβ、Xδ,将Xα的坐标作为PI参数;
步骤4:按照式(18) -(21)更新灰狼个体位置;
步骤5:判断算法终止条件(是否大于最大迭代次数M),若满足,执行步骤6;否则,迭代次数N+ 1,然后执行步骤3;
步骤6:输出PI参数值,算法运行结束。
仿真时,设定算法的最大迭代次数为100,灰狼种群规模为30,灰狼个体适应度值的计算选用时间乘以误差绝对值积分(integrated time and absolute error,ITAE)函数指标,即

式中:e(t)为t时刻的期望值与实际值之间的差值。
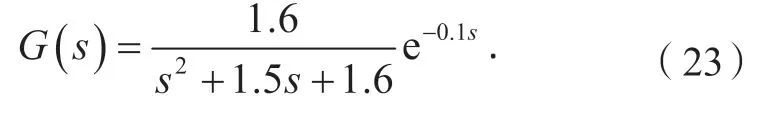
PI闭环控制的Simulink仿真结构如图1所示 (图中,|u|代表绝对值,t代表时间,1/s代表积分),图1中输出端口1即为ITAE函数的输出值。最后得出算法中α狼的适应度值随迭代次数N变化的仿真结果如图2所示。
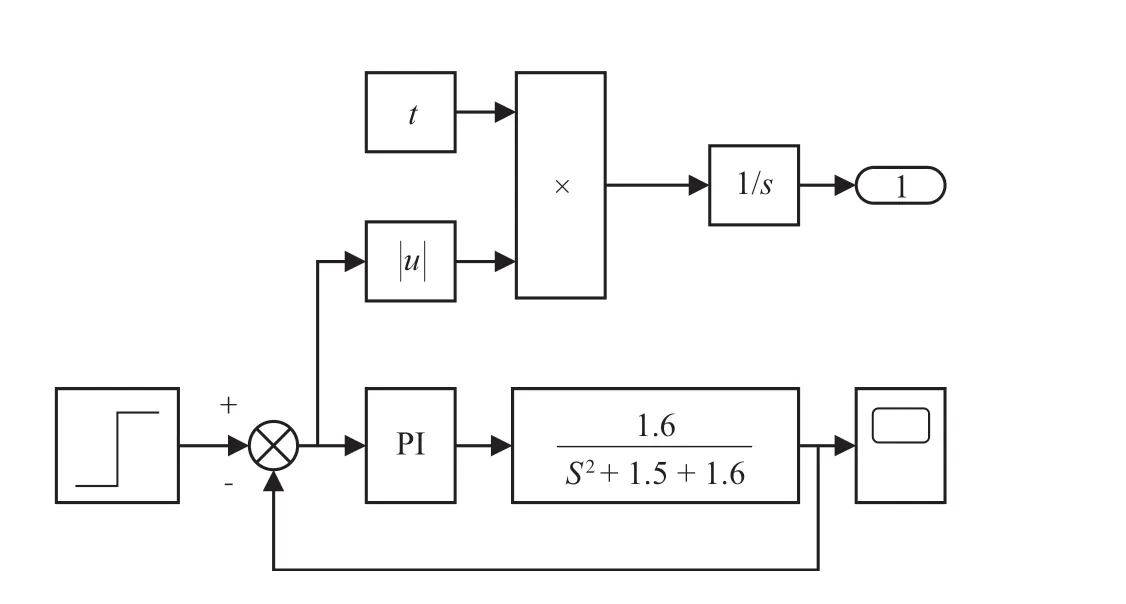
图1 PI控制仿真结构图
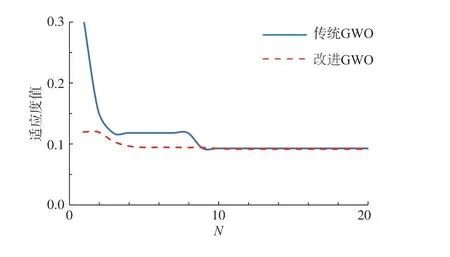
图2 适应度值变化图
由图2可知:与传统GWO算法相比,改进后的GWO算法收敛速度更快,结果更精确,由此证明改进措施是可行的。
4 建模与仿真分析
利用Matlab/Simulink建立基于d轴定子电流id=0的PMSM转速电流双闭环矢量控制系统模型,图3所示为其结构框图。
图3中:n*为电机转速给定值;id*、iq*分别为d-q轴坐标系下的定子电流给定值;iα、iβ与uα、uβ分别为α-β轴坐标系即两相静止坐标系下的定子电流和电压;iA、iB、iC为A-B-C轴坐标系即三相静止坐标系下的定子电流;Clark、Park与Park-1均为坐标变换法,SVPWM为空间矢量脉宽调制技术。
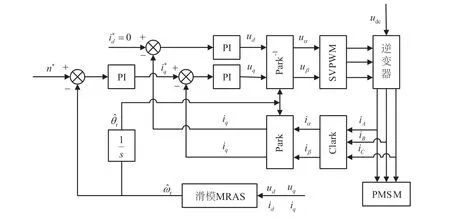
图3 PMSM滑模MRAS结构图
转速环与电流环控制器采用PI控制,传统转速与转子位置传感器由滑模MRAS这一无传感器控制技术代替以实时观测电机转速与转子位置,滑模MRAS部分分别采用传统滑模MRAS和改进的新型滑模MRAS。
设定PMSM的各参数为:定子电阻Rs= 2.875 Ω,定子电感Ls= 8.5 mH,转子磁链ψf= 175 mWb,转动惯量J= 0.8 g·m2,粘滞摩擦系数B= 1 mN·m·s,极对数pn= 4,直流母线电压Udc= 300 V; 转速环PI参数:kp= 10,kI= 25;电流环PI参数:kp= 1 000,kI= 2 000;传统积分滑模面即式(6)中PI参数:Kp= 58,KI= 150;新型滑模面即式(9)中指数参数:g= 7,h= 3,p= 5,q= 3;传统转速观测器即式(7)中参数:λ= 950。
新型转速观测器即式 (10)中参数:λ= 950,α= 0.65,γ= 4。
本文利用改进GWO算法来优化新型滑模面即式(10)中的各项系数a、b与c,优化步骤同3.3章节,适应度函数同式(22),且其误差项最后通过仿真可得系数a、b与c随迭代次数N的变化曲线如图4所示。从图4可知:最终优化所得参数为a=4.243,b= 2.706,c= 2.512。

图4 参数值变化
设定仿真工况如下:
工况1:参考转速为1 000 r/min,负载为2 Nm,仿真时长0.8 s;
工况2:初始时刻参考转速为1 000 r/min,在0.4 s升至1 500 r/min,在0.6 s降至1 200 r/min;负载初始为2 Nm,在0.4 s升至6 Nm,在0.6 s升至10 Nm,仿真时长0.8 s。
在工况1和工况2下所得的仿真结果分别如图5 (见下页)与图6所示(见下下页)。
从图5、图6中的转矩响应曲线可看出:在工况1下的零时刻以及在工况2下的零时刻、0.4 s与0.6 s时,需要变化转速,因此转矩会产生一定的超调或下降,但均在极短的时间内得到了恢复。然而,相比于传统滑模MRAS,改进后的新型滑模MRAS的转矩脉动幅度在两种工况下能够减小75%以上,且去除了波形毛刺,平滑了响应信号。
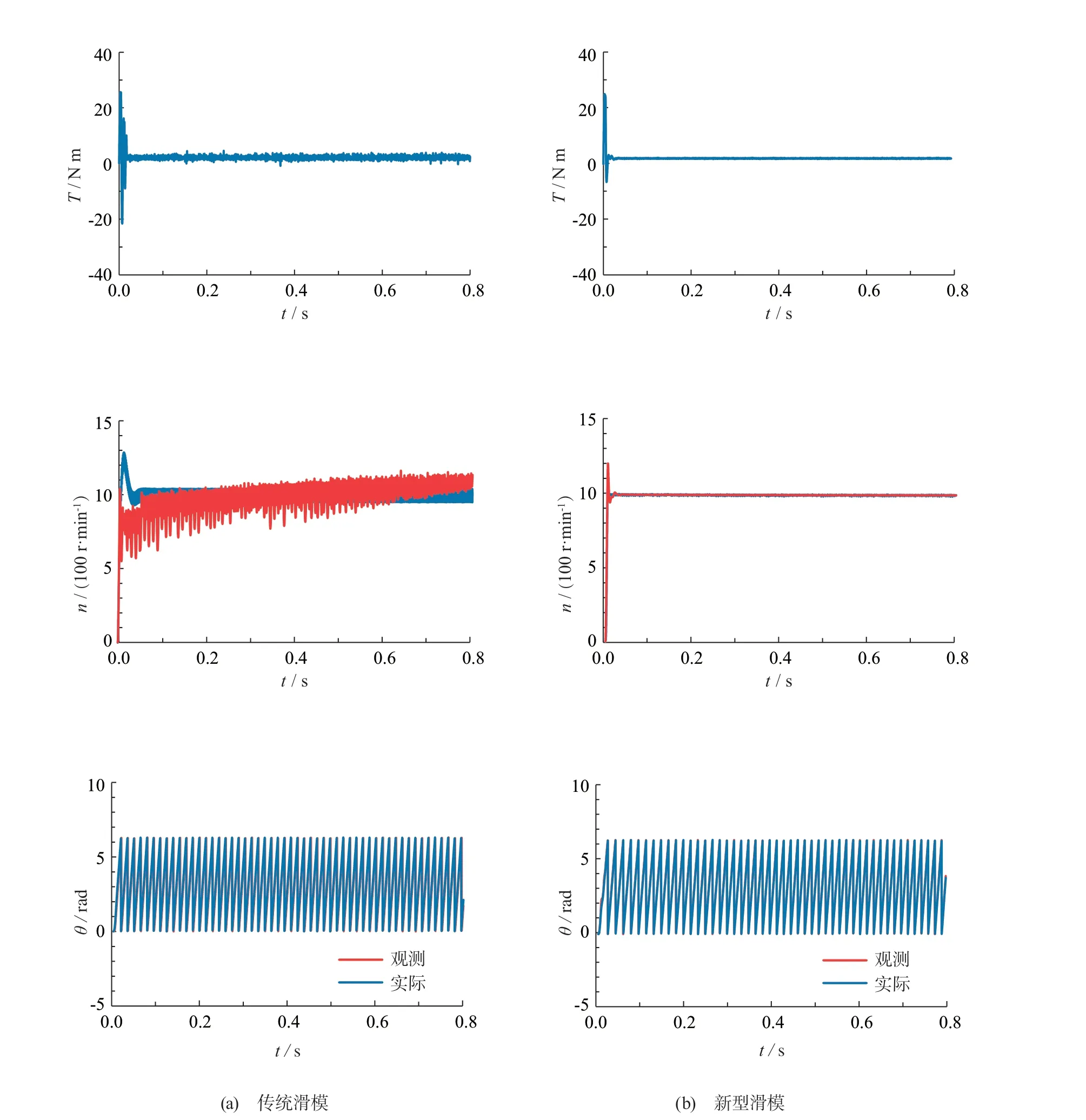
图5 工况1下滑模MRAS响应曲线
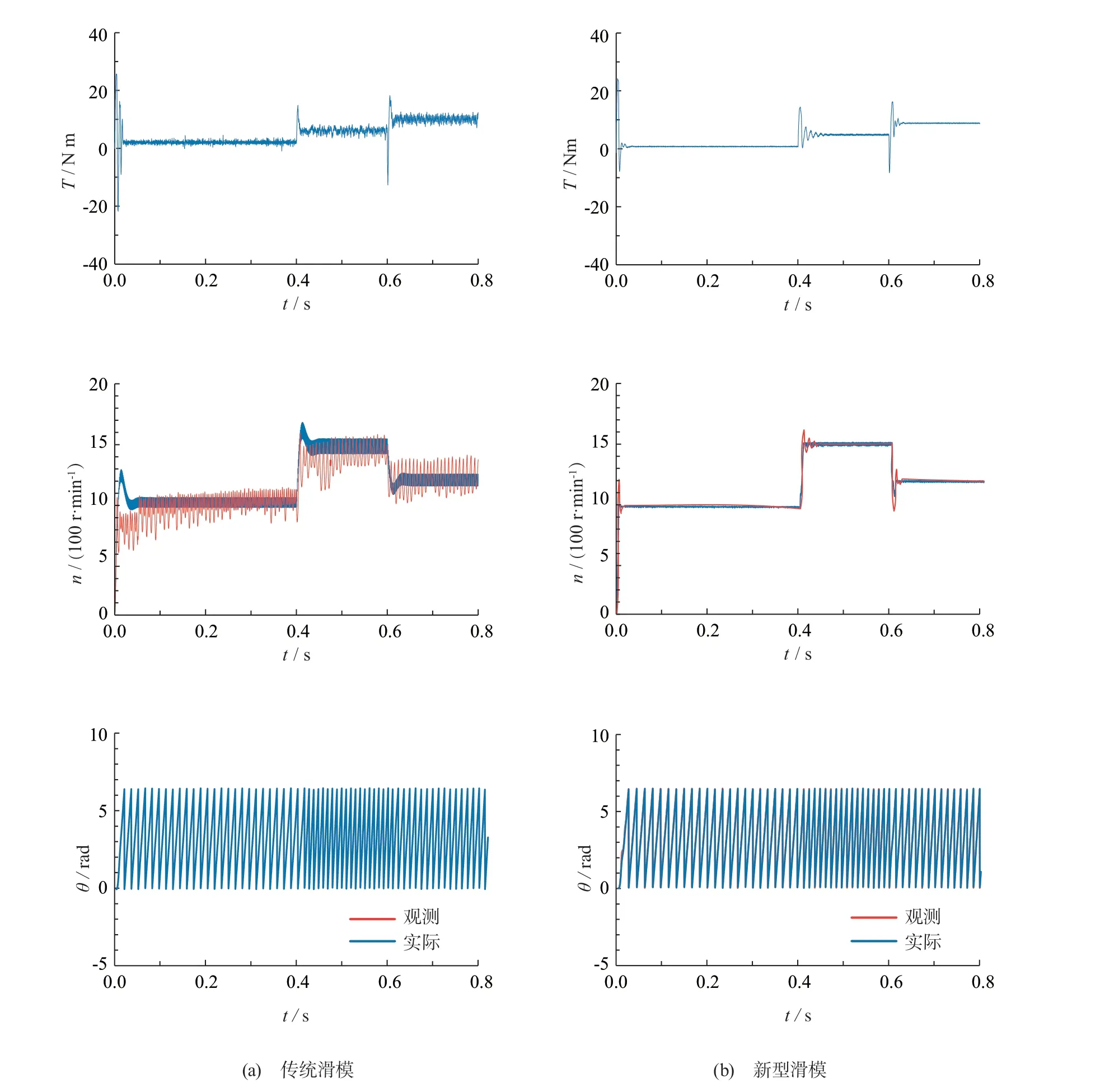
图6 工况2下滑模MRAS响应曲线
从转速响应曲线可看出:传统滑模MRAS的实际转速存在较大抖振,实际转速在工况1下零时刻的超调约为25 %且调节时间约为40 ms,在工况2下零时刻的超调和调节时间与工况1大致相同,在0.4 s时超调约为13.3 %且调节时间约为40 ms,在0.6 s时约下降16.7 %且调节时间约为40 ms;观测转速与实际转速相差颇大,基本失去了准确地跟踪能力。而与传统滑模MRAS相比,2种工况下新型滑模MRAS的实际转速超调与调节时间能够保持在2.3%与10 ms以内,且波形抖动幅度降低了近80%以上,观测转速能有效地对实际转速进行精确跟踪。
从转子位置角响应曲线可看出:在2种工况下,改进后的滑模MRAS较传统滑模MRAS能够将转子位置角观测值与实际值之间的误差减小60%以上,有效地提高了观测精度。
此外,传统控制方法下的转子位置角响应周期比新型控制方法下的周期要短,其原因为传统方法所带来的转速抖振较大,转速可到达的上限值较高,由此使得转子每次到达相同位置角时所用时间较少。
5 结 论
本文在传统永磁同步电机(PMSM)滑模模型参考自适应系统(MRAS)基础上,设计了一种新型滑模MRAS,利用改进的灰狼优化(GWO)算法对其相关参数,进行寻优整定。进行了仿真实验。
结论是:与传统滑模MRAS相比,改进的新型滑模MRAS能将系统转矩脉动幅度减小75%,实际转速抖动幅度减小80%,超调控制在2.3%以内,调节时间控制在10 ms以内,转子位置观测误差减小60%。这使得PMSM动态与静态控制性能得到了进一步增强。
参考文献 (References)
[1] 尚飞, 霍海波. 永磁同步电机滑模变结构MRAS转速辨识[J]. 电气传动, 2017, 47(2): 9-14.
SHANG Fei, HUO Haibo, Sliding mode variable structure MRAS speed estimator for permanent magnet synchronous motors [J].Electric Drive, 2017, 47(2): 9-14.(in Chinese)
[2] 李垣江, 董鑫, 魏海峰, 等. 基于改进模型参考自适应系统的永磁同步电机参数辨识[J]. 控制理论与应用, 2020,37(9): 1983-1988.
LI Yuanjiang, DONG Xin, WEI Haifeng, et al. Parameter identifification method of permanent magnet synchronous motor based on improved model reference adaptive system[J].Control Theory Appl, 2020, 37(9): 1983-1988. (in Chinese)
[3] 齐洪峰, 王轶欧, 闫一凡. 无速度传感器永磁同步电机预测电流控制策略[J]. 北京交通大学学报, 2020, 44(2):119-128.
QI Hongfeng, WANG Yi’ou, YAN Yifan. Predictive current control strategy of permanent magnet synchronous motor without speed sensor [J].J Beijing Jiaotong Univ,2020, 44(2): 119-128. (in Chinese)
[4] Sahhary B, MA Zhixun, Kennel R, et al. Sensorless speed control of PMSM based on MRAC using active power [J].EPE J(Euro Power Elect Drives J), 2015, 25(2): 18-25.
[5] 缪仲翠, 王志浩, 李东亮, 等. 基于FOSM-MRAS观测器的永磁同步电机MPTC系统[J].电机与控制学报,2020, 24(4): 121-130.
MIAO Zhongcui, WANG Zhihao, LI Dongliang, et al.Permanent magnet synchronous motor MPTC system based on FOSM-MRAS observer [J].Electric Mach Control, 2020, 24(4): 121-130. (in Chinese)
[6] Kim J S, Sul S K. New approach for high performance PMSM drives without rotational position sensors [J].IEEE Trans Power Electronics, 1997, 12(5): 904-911.
[7] 齐放, 邓智泉, 仇志坚, 等. 基于MRAS的永磁同步电机无速度传感器[J]. 电工技术学报, 2007(4): 53-58.
QI Fang, DENG Zhiquan, QIU Zhijian, et al. Sensorless technology of permanent magnet synchronous motors based on MRAS [J].Trans Chin Elec-tech Soc, 2007(4):53-58. (in Chinese)
[8] Samat A A A, Ishak D, Iqbal S, et al. Comparison between takagi sugeno FIS and PI controller: an adaptation scheme of MRAS for speed sensorless control of PMSM [J].Appl Mech Mate, 2015, 4079(5): 193-197.
[9] Zolfaghari M, Taher S A, Munuz D V. Neural networkbased sensorless direct power control of permanent magnet synchronous motor [J].Ain Shams Engineering J,2016, 7(2): 1-12.
[10] 钟臻峰, 金孟加, 沈建新. 基于分段PI调节器的模型参考自适应永磁同步电动机全转速范围无传感器控制[J].中国电机工程学报,2018, 38(4): 1203-1211+1297.
ZHONG Zhenfeng, JIN Mengjia, SHEN Jianxin. Full speed range sensorless control of permanent magnet synchronous motor with phased PI regulator-based model reference adaptive system [J].Proc CSEE, 2018, 38(4):1203-1211+1297. (in Chinese)
[11] 林茂, 李颖晖, 吴辰, 等. 基于滑模模型参考自适应系统观测器的永磁同步电机预测控制[J].电工技术学报,2017, 32(6): 156-163.
LIN Mao, LI Yinghui, WU Chen, et al. A model reference adaptive system based sliding mode observer for model predictive controlled permanent magnet synchronous motor drive [J].Trans Chin Elec-tech Soc, 2017, 32(6):156-163. (in Chinese)
[12] 吴伟, 杜昭平. 改进MRAS的永磁同步电机无速度传感器控制策略[J]. 微电机, 2019, 52(12): 53-58.
WU Wei, DU Zhaoping. Speed sensorless control strategy of permanent magnet synchronous motor based on improved MRAS [J].Micromotors, 2019, 52(12): 53-58. (in Chinese)
[13] 滕青芳, 柏建勇, 朱建国, 等. 基于滑模模型参考自适应观测器的无速度传感器三相永磁同步电机模型预测转矩控制[J]. 控制理论与应用, 2015, 32(2): 150-161.
TENG Qingfang, BAI Jianyong, ZHU Jianguo, et al.Sensorless model predictive torque control using slidingmode model reference adaptive system observer for permanent magnet synchronous motor drive systems [J].Control Theory Appl, 2015, 32(2): 150-161. (in Chinese)
[14] 陈威, 董秀成, 周单, 等. 改进滑模模型参考自适应的PMSM无传感控制[J]. 计算机应用研究, 2019, 36(12):3 788-3791.
CHEN Wei, DONG Xiucheng, ZHOU Dan, et al.Sensorless control of PMSM based on improved slidingmode model reference adaptive system method [J].Appl Res Computers, 2019, 36(12): 3788-3791. (in Chinese)
[15] Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer[J].Adv Engineering Software, 2014, 69(5): 46-61.
[16] 张小青, 李艳红. 基于灰狼优化算法的神经网络PMSM混沌同步控制[J]. 云南大学学报(自然科学版) , 2020,42(4): 664-672.
ZHANG Xiaoqing, LI Yanhong. PMSM chaos synchronization control of neural network based on grey wolf optimizer algorithm [J].J Yunnan Unive(Nat Sci Ed), 2020, 42(4): 664-672. (in Chinese)
[17] 陈琦, 王旭刚. 非奇异快速终端滑模及动态面控制的轨迹跟踪制导律[J]. 国防科技大学学报, 2020, 42(1): 91-100.
CHEN Qi, WANG Xugang. Trajectory tracking using nonsingular fast terminal sliding mode control and dynamic surface control [J].J National Univ Defense Tech, 2020, 42(1): 91-100. (in Chinese)
