量子叠加态中的时空非连续性

曹峻峰

（大连依诺维电气有限公司技术研发部，辽宁大连 116600）

0.引言

1900年，马克斯·普朗克通过《论正常光谱的能量分布定律的理论》论文提出了量子力学理论；1905—1918年，阿尔伯特·爱因斯坦通过多篇论文提出了狭义相对论与广义相对论，并推导出了引力波的存在；1926年，尔温·薛定谔通过《作为本征值问题的量子化》论文进一步用数学方程诠释了微观世界的量子特性；1926年，马克斯·玻恩通过对波函数的统计学解释提出了几率波的概念，并为之后出现的量子叠加态概念奠定了理论基础。

随着时间的推移几代科学家们用了200多年的时间，通过大量的实验，几经周转在物理学的前沿阵地铸造了一个个辉煌的里程碑。不过直到今天我们仍然徘徊在量子力学不得其解的观测结果中久久停滞不前，其中量子呈现叠加态即为一个很难用常理解释的观测结果。本文将结合广义相对论中的光锥模型推导分析，根据量子叠加态的观测结果建立一个多维时空模型，并在该模型体系的基础上讨论存在高维时空的可能性以及量子信息的叠加问题；另外本文在引力波这种可观测的物理现象的基础上讨论时空在微观尺度的波动性与非连续性。最终假设推导出逻辑通顺，简洁合理的叠加态形成解释，以供该领域学者参考讨论。

1.量子叠加态的观测结果

在宏观世界，物体在某一时刻永远都处于某一个确定的位置，并与其观测者之间只存在一个确定的相对速度，这也可以总结为宏观世界中物体呈现位置与速度的确定性。而在微观世界中粒子不再遵循宏观世界的确定性原则，其观测结果为粒子在某一时刻同时处于两个或两个以上的位置，并以相对观测者不同的速度同时存在，也就是在同一时刻的某个局部区域内，微观粒子以不同的运动速度同时处在多个位置，并且这些不同状态同时叠加到一起被观测者观测到，这种状态就是量子的叠加态。

量子叠加态也同样适用于对原子核外电子的观察，电子是一种微观粒子，在原子内部（即直径约10-10m）的微小空间运动。核外电子的运动没有确定的方向和轨迹，其在原子核周围有的区域出现的次数多，有的区域出现的次数少，就像“云雾”一样笼罩在原子核的周围。因此科学家们在此观测结果的基础上提出了“电子云模型”，并用电子云来描述电子在原子核外空间某区域出现机会的大小（即出现几率）。其中电子云密度大的地方，表明电子在核外单位体积空间内出现的机会多，反之出现的机会少（如图1所示）。

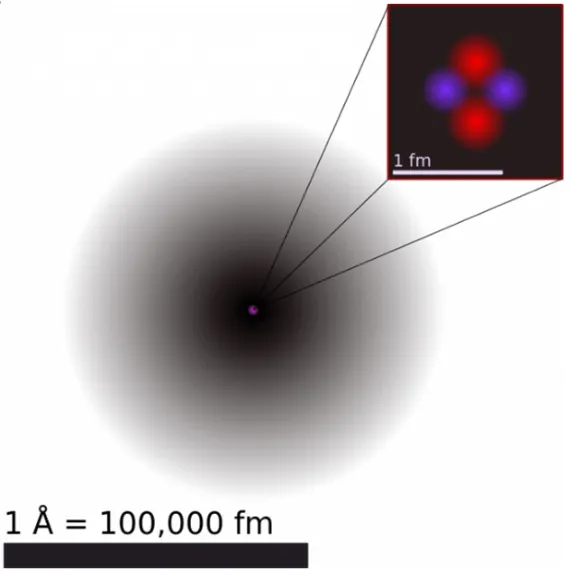
图1 氢原子在观测过程中的叠加态成像

2.量子叠加态的光锥模型

光锥模型源自于爱因斯坦狭义相对论，在这个模型体系中,时空被定义为四个维度，三个空间维度和一个时间维度[1]。其中三个空间维度指的就是我们生活在其中的这个由三维坐标系构成的立体空间，一个时间维度就是把我们生活中的时间看成一个一维变量，类似于一条朝着一个方向延伸的直线，并且其延伸趋势不可逆[2]。

而光锥模型就是将三个空间维度等效为一个二维平面（以下简称三维空间平面），将一个时间维度等效为一条垂直于此平面的直线（以下简称一维时间直线），以此组成可描述时空变化的模型（如图2所示）。

图2 狭义相对论中的光锥模型

图中的平面即为现在，事件发生之点为原点，三维空间中，物体随时间变化生成的信息会以光速c在三维空间中向外传播（其中光速c为宇宙速度的上限，物体经历的时间为t）[3]。因此物体本身触发的事件所能影响的空间范围为以ct为半径所包围的圆形区域（在三维坐标系中该区域是个球体，在将三维坐标系等效为二维平面后，该区域即为一个圆）。随着时间的改变，这个圆形区域在光锥模型中沿着时间直线延伸的方向逐渐变大，并在其向上（未来）的方向上逐渐连续变大，合并成倒立的锥体，即物体的未来光锥；同样下面与之对称的正立锥体是物体的过去光锥。一个事件的光锥界定了它的时空边界，光锥以内的其他事件可以跟它有关，光锥以外的事件必定跟它无关。

因此，我们可以在此基础上构建宏观世界观测者与被观测物体之间的光锥模型（如图3-a）。我们在观测宏观世界物体时，物体发出或反射的光被观测者接收的这段时间里，物体和观测者同时沿着各自的一维时间直线向上延伸，物体发出或反射的光所经过的最大空间尺度也随之形成光锥，当光锥边缘与观测者的一维时间直线产生交点时，即为该物体被观测者观测到，此时即可生成相应的观测结果。

同样，我们可以对比宏观世界中物体的光锥模型来构建微观世界中粒子的光锥模型，即量子叠加态的光锥模型。根据量子叠加态的观测结果，我们可反向还原粒子反射的光被观测者接收的这段极短时间里，粒子与观测者之间生成的光锥模型（如图3-b，由于作图精度有限，这里并未将所有光锥全部体现，省略了大部分光锥，以均匀排列方式示意，以便读者理解）。在光锥模型中，观测者对任意物体或粒子生成观测结果均需该物体或粒子在其所在位置上发射或反射的光被观测者接收，同时，模型中物体或粒子生成的光锥边缘与观测者的一维时间直线产生交点。因此，叠加态的观测结果形成时，对于同一个粒子在不同位置出现的影像也会生成多个交于观测者一维时间直线同一点的光锥，通过图3-b我们发现，在这极短的时间里同一个粒子同时生成了多个平行的光锥。我们将图3-b中的粒子光锥和观测者一维时间直线过滤掉可以看到同一个粒子在四维时空中同时存在的多条平行一维时间直线（如图3-c）。根据图3-c中的还原结果，我们便可大胆推测在量子观测层面，时间被观测到了更多的维度信息。这些多出来的时间维度信息通过某种方式叠加到我们所在的四维时空中，进而干扰了我们对微观粒子的观测结果。最终，这种被干扰的观测结果即为量子的叠加态。

图3 宏观物体与微观粒子叠加态的光锥模型示意图

3.高维时空推论

根据量子叠加态的光锥模型，我们发现一个粒子在同一时间出现了多个一维时间直线，这个结果在我们四维时空中是解释不通的，因为在四维时空中设定时间本身只有一个维度，想要实现多个一维时间直线同时存在就需要时间本身像空间一样具有比一维更高的维度。这里我们就需要将时间从一维升维，假设时间存在二维（即时空存在五维），那么就可以在二维时间平面上同时画出多条平行的一维时间直线（如图4-a，由于目前我们所在的世界并未发现与其他时空相交或重叠的现象，所以这里假设一维时间直线在高维度中为彼此平行的状态）。不过从逻辑上讲，在二维时间平面参考系中，一维时间直线A中的观测者最多能观测到除自身所在一维时间直线以外的两条平行一维时间直线中的信息，即平面上左边的一维时间直线B与右边的一维时间直线C中的信息。除此以外，其他的一维时间直线中的信息，均因二维时间平面的局限性被B与C遮挡住，无法被A中的观测者观测到（如图4-b）。

但是在量子叠加态的光锥模型中，粒子观测结果所生成一维时间直线的数量远大于2，这里我们就需要将时间从二维再度升维，假设时间存在三维（即时空存在六维），那么就可以在三维时间立方体（三维时间立方体是为了方便作图理解的假设形式，还可以是球体或无边界形式等）中同时画出多条平行的一维时间直线（如图4-c）。这样从逻辑上讲，在三维时间立方体参考系中，一维时间直线A中的观测者即可观测到除自身所在一维时间直线以外360°视角范围内的多条平行一维时间直线中的信息，即立方体中的其他一维时间直线B1、B2、B3…Bn中的信息。在这个假设条件下，A中的观测者才有可能观测到更多数量的一维时间直线中的信息，并在同一时间将多个观测信息叠加。即在这种情况下的观测结果才有可能呈现量子叠加态在光锥模型中的还原结果。

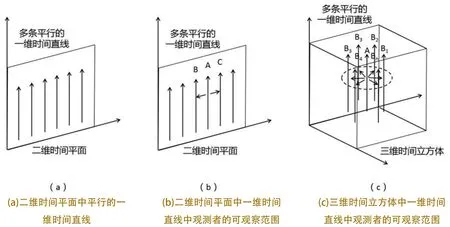
图4 一维时间直线在二维、三维中的概念图

因此，根据量子叠加态的光锥模型，我们不仅可以推测时间本身存在更高的维度；并可根据模型还原结果分析得出时间存在的维度大于等于三维，即时空存在的维度大于等于六维。

4.时空的波动性

根据广义相对论，我们知道时空可以在能量或质量的作用下弯曲，近年来引力波的观测结果也同样揭示了时空不但可以随之弯曲，还可以随着能量或质量的剧烈变化在宏观尺度上出现波动。这就好比向平静的水面投入石子所产生的波状涟漪。在石子进入水面的瞬间，水面原本的平衡状态被石子打破，石子在重力的作用下将平整的水面向下撕裂，水分子在范德华力的作用下随之恢复原有的平衡状态，这个过程最终促成了水面的波动，这也是水以及其他流体介质所具有的波动性。在某种层面上，时空也具有相似的性质，引力波的出现即为时空原有的平衡状态被能量打破的结果，进而时空产生了波状涟漪。这也可以理解为能量与质量的剧烈变化对时空的撕裂效应，时空在其自身属性的作用下随之恢复原有的平衡状态，这个过程便促成了时空的波动。引力波是在高能级能量变化过程中形成的宏观尺度时空波动。相对而言，微观粒子所引起的微小能量变化，则无法在宏观尺度上观测到相应的时空波动现象。不过根据通常情况下影响效果与能量变化之间的线性递减规律，也许微小的能量变化可以在微观尺度上引起极小的时空波动，并且这种微观尺度的时空波动亦有可能影响到我们对微观粒子的观测结果。即量子在波粒二象性中的波动特性有可能源于微观尺度的时空波动。

5.时空在量子尺度上的非连续性假设

从微观角度讲，水面是由一个个微小的水分子在范德华力的作用下紧密排列而成，水面的波动现象也是水分子间依次往复运动的结果。如果时空也同样存在类似水分子的最小单元，并且这些最小单元之间并不是绝对连续的（即这些最小单元像构成水面的水分子一样，其相互间的联系可以被某种能量瞬间撕裂，并在时空自身属性的作用下，以往复运动的形式瞬间恢复平衡），那么时空在其最小单元所在的微观尺度上就很可能出现类似宏观尺度的波动现象。因此，当我们假设时空在量子尺度上是非连续性的，即时空在微观尺度上存在最小单元，那么我们很可能在量子尺度上观测到粒子能量变化所引起的时空波动现象。即微观粒子运动过程中所引起的时空波动。

物质是非连续性的，所以我们在极小的空间尺度上观测到了组成物质的最小单元分子或原子（目前观测到的最小单位有夸克、胶子、波色子、费米子等微观粒子，这些均为构成物质最小单元的基础元素）。因此，如果时空是非连续性的，组成时空的最小单元也同样会出现在极小的空间尺度上。其最小时空单元的边界犹如屏幕像素之间的黑线，有可能与我们所在的四维时空成垂直状态，在正常情况下不可观测（如图5-a），但是在时空被某种能量瞬间撕裂的情况下，其最小单元的边界处就有可能出现微小的时空裂缝（如图5-b）。这些时空裂缝会受到时空自身属性的作用，以波动的形式瞬间恢复原状。但在波动的过程中，其他四维时空的量子信息就有可能被瞬间叠加进来（如图5-c）。如上文所述，当时间存在三维（即时空存在六维）时，六维时空的信息就有可能通过我们四维时空的时空裂缝叠加进来，并且这种叠加现象仅存在于产生时空裂缝的微观尺度上。如果叠加进来的信息是同一个微观粒子在其他四维时空中的空间位置与相对速度信息，那么在这种原理的作用下我们就可以观测到量子呈现叠加态的观测结果。当然这需要上述假设全部成立的前提下，才有可能实现。

图5 时空在量子尺度上的非连续性与波动性示意图

综上所述，在假设时空存在六维的前提下。如果时空在量子尺度上是非连续性的，那么便会在极小的空间尺度上存在时空的最小单元。最小时空单元之间有可能会在一定能量或质量的作用下（如微观粒子的高速运动）被瞬间撕裂，出现微小的时空裂缝。该时空裂缝会在时空瞬间恢复原平衡后消失。整个过程中，最小时空单元间依次往复运动形成了微观尺度的时空波动，这种量子尺度的时空波动会将其他四维时空中的量子信息，通过瞬间出现的微小时空裂缝叠加进我们所在的四维时空中。最终，随着微观粒子高速运动所引起的量子尺度时空波动，同一粒子在其他四维时空中的位置与速度信息有可能通过不断出现的微小时空裂缝叠加进我们所在的四维时空中。这些信息在同一时间被观测者接收，进而生成了量子叠加态的观测结果。

6.结论

（1）根据量子叠加态的光锥模型，我们发现一个粒子在同一时间出现了多个一维时间直线，想要实现多个一维时间直线同时存在就需要时间本身像空间一样具有比一维更高的维度。（2）根据量子叠加态在光锥模型中的还原结果，可分析得出时间存在的维度大于等于三维，即时空存在的维度大于等于六维。（3）根据通常情况下影响效果与能量变化之间的线性递减规律，可推测微小的能量变化有可能在微观尺度上引起极小的时空波动，并且这种微观尺度的时空波动亦有可能影响到我们对微观粒子的观测结果。即量子在波粒二象性中的波动特性有可能源于微观尺度的时空波动。（4）如果时空存在最小单元，并且这些最小单元之间并不是绝对连续的，那么时空在其最小单元所在的微观尺度上就有可能出现类似宏观尺度的波动现象。（5）最小时空单元的边界犹如屏幕像素之间的黑线，有可能与我们所在的四维时空成垂直状态，在正常情况下不可观测，但是在时空被某种能量瞬间撕裂的情况下，其最小单元的边界处就有可能出现微小的时空裂缝。（6）在假设时空存在六维的前提下，六维时空的信息有可能通过我们四维时空的时空裂缝叠加进来，并且这种叠加现象仅存在于产生时空裂缝的微观尺度上。（7）量子尺度的时空波动有可能将其他四维时空中的量子信息，通过瞬间出现的微小时空裂缝叠加进我们所在的四维时空中。（8）随着微观粒子高速运动所引起的量子尺度时空波动，同一粒子在不同四维时空的量子信息，有可能在同一时间被观测者接收，进而生成了量子叠加态的观测结果。