基于绿证-碳交易机制的含风电电力系统动态环境经济调度
2021-10-13张家瑞余朋军许忠义徐加宝朱泽伟
张家瑞,余朋军,许忠义,徐加宝,朱泽伟
(三峡大学电气与新能源学院,湖北宜昌 443002)
0 引言
近年来,环境污染及化石能源短缺等问题日益突出。为促进经济结构绿色转型,我国于2020 年9月第七十五届联合国大会上提出碳达峰、碳中和目标[1]。为实现“双碳”目标、减少污染物排放、促进可再生能源的发展,同时引入绿色证书交易机制和碳排放交易机制(以下简称碳交易),对于电力系统节能减排和绿色低碳发展有着重要的意义。
目前国内外学者对碳交易机制和绿色证书交易机制已有较为深入的研究[2-5]。文献[6]将碳交易机制引入到含风电的电力系统经济调度模型中,使碳排放权成为一种有经济价值的资源,建立了一种兼顾系统经济性和系统环保性的新型经济调度模型。文献[7]将绿色证书交易机制和碳交易机制引入到电源规划模型中,建立了以规划期内系统净收益最大为目标的低碳经济电源规划模型。文献[8]将绿色证书交易机制引入电力系统调度模型中,建立了基于绿色证书交易机制的含风电系统的低碳经济调度,并对不同绿色证书约束水平对系统成本以及碳排放量的影响进行了分析。文献[9]将碳交易引入到冷热电联供系统的经济调度模型中,建立考虑碳交易成本、燃料成本和环境成本的冷热电联供系统多目标优化模型。以上文献都只是孤立地将碳交易机制或者绿色证书交易机制应用在电力系统中,并未在电力系统多目标调度模型中同时考虑2种交易机制。
电力系统的环境经济调度(Environmental Economic Dispatch,EED)问题是一个典型的高纬度、非凸、非线性且强约束的多目标优化问题[10-12]。目前,求解多目标优化问题的方法有间接法和直接法。(1)间接法将多目标问题转化成单目标问题,如何进行转化是间接解法的关键。然而将多目标问题转化成单目标问题,其各目标的参数设置是未知的、不确定的,容易对求解结果产生较大的影响。因此,目前间接法求解多目标优化问题难以得出令人满意的结果。(2)相较于间接解法,直接解法搜索效率高、鲁棒性强、不易陷入局部最优[13]。求解多目标优化问题的直接解法主要有非支配排序遗传算法(NSGA-П)[14]、多目标粒子群(MOPSO)[15]、基于分解的多目标进化算法(MOEA/D)[16]等。尽管这些算法取得了不错的效果,但也存在着收敛速度慢、运行耗时长以及种群多样性丧失等缺点[17]。如何改善算法效率、均衡算法收敛性和保持种群多样性是高效求解EED问题的关键。
基于以上讨论,本文将碳交易机制和绿色证书交易机制同时引入电力系统EED 中,构建计及碳交易机制和绿色证书交易机制的含风电的电力系统多目标环境经济调度模型:在经济调度目标模型中引入弃风惩罚机制,提高风电的适应性;同时引入旋转备用容量调度模型应对风电及负荷预测不确定性对电力系统产生的不利影响,提出一种基于反向学习混沌搜索多变异策略(OLSMS)的多目标进化算法MOEA/D-OLSMS 对模型进行求解。该算法在MOEA/D 的基础上,采用广义反向学习初始化种群扩大种群多样性,并采用DE/rand/1 和DE/currentto-rand/1 策略进行进化,同时引入基于Logistic 映射的混沌搜索算法增强算法的局部搜索能力。仿真验证结果证明了该模型的合理性、有效性以及MOEA/D-OLSMS算法的可行性、优越性。
1 计及绿证-碳交易机制的含风电电力系统EDD模型
1.1 绿色交易证书机制数学模型
绿色证书交易机制是可再生能源配额制的辅助政策工具。其中,可再生能源配额指标是指政府规定发电企业中可再生能源发电量要达到或占有总发电量一定的比例。政府将发电企业生产的绿色电能可以按比例量化为绿色证书。当发电企业生产的绿色证书超过配额指标时,可出售绿色证书获取利润;反之,则需要为购买绿色证书。其绿色证书交易成本模型如下


1.2 碳交易机制数学模型
目前,世界范围内初始碳分配额主要有免费分配、拍卖分配、免费分配与拍卖混合分配3 种方式。我国主要采用免费分配的方式。在政府免费分配给企业一定碳排放权配额的情况下,当企业实际产出的碳排放量大于给定配额时,需要在市场上购买碳排放配额;反之,可以在市场上出售碳排放配额以获取利润。
(1)碳排放模型。

式中:Eq为火电机组碳排放配额;δq,i为发电机组i单位电量分配的碳排放配额,由国家发改委规定的“区域电网基准线排放因子”确定。
(3)碳交易模型。

1.3 机组成本
考虑阀点效应,火电机组的发电成本费用目标函数为
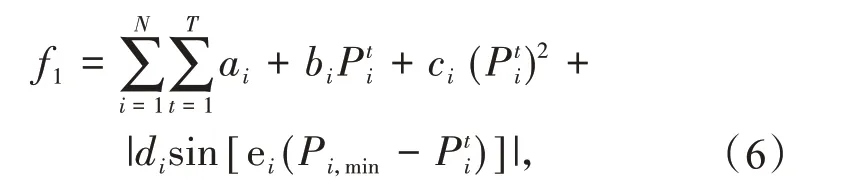
式中:ai,bi,ci,di,ei为机组i的成本费用系数;Pi,min为机组i的出力下限。
1.4 风电场运行成本
1.4.1 风电运行维护成本
为了促进可再生能源的利用,将风电进行大规模并网,风电场在运行过程中虽然无能源消耗,但会产生运行维护成本,其数学模型为

1.5 污染物排放量目标函数
火电机组在运行中会产生大量污染环境的气体,以CO2,SO2及NOx等气体为主,其中CO2主要参与碳交易,气体污染物排放以SO2及NOx为主,污染物的排放量(E)用一定的权重系数来表示,

式 中:γi,S,βi,S,αi,S为 机 组i的SO2排 放 特 征 系 数;γi,N,βi,N,αi,N为机组i的NOx排放特征系数;ei为SO2的权重系数;hi为NOx的权重系数。
1.6 约束条件

(2)系统旋转备用容量约束。为了应对风电出力不确定性对系统的影响,系统需要预留一定的备用容量。

2 MOEA/D-OLSMS算法
本文在MOEA/D 算法的基础上,结合OLSMS 提出了一种MOEA/D-OLSMS优化算法。
2.1 MOEA/D算法
MOEA/D 算法框架由模型分解和进化搜索组成:首先将多目标优化问题分解为一系列的子问题;然后利用单目标进化算法求解每个子问题。MOEA/D 算法是于2007 年提出的一种新颖的求解多目标问题优化算法,包括模拟二进制交叉(Simulated Binary Crossover,SBX)和 差 分 进 化(Differential Evolution,DE)[18-20]2 种进化算子。本文采用了DE进化算子。
DE进化算子主要通过变异、交叉和选择操作进行智能搜索。算法一般设置NP个种群,每个个体的维度为n,个体表示为xi,G=(x1i,G,x2i,G,…,xni,G),其中种群个数i=(1,2,…,NP),G为当前种群的进化代数。
(1)策略1,若采用目前被广泛使用的DE/rand/1变异策略,可得到
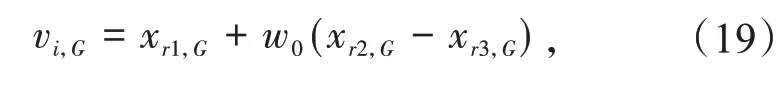
式中:vi,G为第G代种群变异后生成的第i个体;xr1,G,xr2,G,xr3,G为从种群规模中随机产生3 个互不相等的个体,而xbest,G为当前最优个体;w0为缩放因子。
若采用DE/current/1变异策略,
上述分析可见,DE进化算子关键部分是变异操作。不同的变异策略所具有的特性不一样,DE/rand/1 变异策略具有全局搜索能力突出、较强的全局收敛性能,且倾向于开采能力,DE/best/1 变异策略全局搜索能力弱,局部寻优能力和倾向于探索能力,收敛速度快[20]。DE/current-to-best/1 变异策略同时具有DE/rand/1 和DE/best/1 的特性,被广泛用于各类算法。
(2)策略2,根据DE/current-to-best/1 变异策略改进得到DE/current-to-rand/1变异策略,
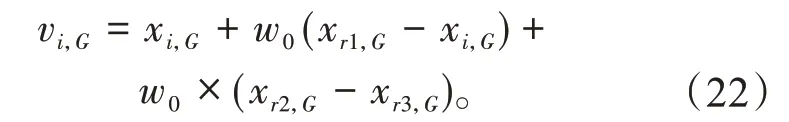
2.2 反向学习混沌搜索多变异策略OLSMS
2.2.1 反向学习原理
反向学习由Tizhoosh[21]于2005 年提出,其主要思想是根据当前解得出反向解,并从当前解和反向解中择优选取候选解。

式中:X为一个可行解;Xˉ为X的反向解;X0为当前解和反向解中的最优解。
2.2.2 基于Logistic映射的混沌搜索
混沌搜索具有遍历性、随机性和规律性等特点[22],根据这些特点可以不重复地遍历整个搜索空间。本文采用了Logistic 映射法,其具体数学表达式为

(4)根据混沌搜索生成的新解,计算其适应度值,并比较新解适应度值和原解适应度值的大小,更优的解进入下一次迭代,直至混沌搜索迭代达到最大迭代数,输出混沌搜索的结果;否则,k=k+ 1,转入式(28)。
2.2.3 反向学习混沌搜索多变异策略
将反向学习策略、基于Logistic映射混沌搜索以及多变异策略融入到MOEA/D 算法中,可得其基于反向学习混沌搜索多变异策略的MOEA/D-OLSMS算法步骤。
(1)基于广义反向学习的最优初始种群生成。首先采用随机策略生成最初种群,其次采用广义反向学习策略求出反向种群,根据式(24)生成反向种群,分别计算最初种群和反向种群的个体适应度值,最后根据式(25)来选择最终初始种群。
(2)多变异策略搜索。根据(1)中得出初始种群,先经过策略1 中DE/rand/1 变异、交叉、选择生成当前个体,计算当前个体的适应度值,并保存最优个体和更新种群适应度值,再经过策略2 中DE/current-to-rand/1 策略变异、交叉、选择生成当前个体,计算当前个体的适应度值,并保存最优个体和更新种群适应度值。
(3)基于Logistict 映射混沌搜索。根据(2)中得出最优个体和种群适应度值,对最优解进行混沌搜索得出新解并计算出新适应度值,保存新解和更新种群适应度值,将得出的更优解进入下一次迭代。
2.3 基于MOEA/D-OLSMS 算法的含风电场的电力系统模型求解
2.3.1 参数设置
(1)输入机组数据、风电场数据、绿色证书交易数据、碳交易数据以及日负荷数据。
(2)设置算法中种群规模和子问题个数都为NP,权重向量邻域大小为M0,交叉概率为CR,变异概率为pm,缩放因子为w0,最大迭代次数F1(y)。
2.3.2 算法初始化
(1)采用广义反向学习策略初始化种群F1(y),即机组有功出力,以及初始化权重向量λ={λ1,λ2,λ3,…,λNP}。计算任意2 个权重向量之间的欧氏距离,为每个权重向量选出最近的M0个向量作为它的邻域,则设邻域B(i) ={i1,i2,i3,…,iM},以及进化代数G= 0。

2.3.3 算法更新
(1)根据2.2.1 中所述广义反向学习策略生成初始种群。
(2)根据机组出力约束条件,初始化个体xi经过策略1 中DE/rand/1 变异、交叉、选择修复生成个体y,得到变异修复后的机组出力,代入目标函数计算适应度值Fψ(y),如果zψ>Fψ(y),则zψ=Fψ(y)。
(3)根据步骤(2)的生成个体和适应度值。更新 邻 域B(i),如 果gte(y|λi,z)≤gte(x|λi,z),则x=y,Fψ(x) =Fψ(y),ψ= 1,2,更新得出全局最优个体x和全局最优值Fψ(x)。
(4)全局最优个体x和全局最优值Fψ(x)经过策略2 中DE/current-to-rand/1 策略变异、交叉、选择修复生成个体y',代入目标函数计算得到适应度值Fψ(y')。根据个体y'和适应度值Fψ(y'),同时更新邻域B(i),得出全局最优个体x0和全局最优值Fψ(x0)。
(5)根据2.2.2,对全局最优个体x0和全局最优值Fψ(x0)进行混沌搜索,得出最优个体y0进入下一次迭代。
2.3.4 迭代终止判断
如果G=Gmax,则停止迭代计算,输出Pareto 最优解集。否则,G=G+1,则转到2.3.3的步骤(3)。
2.4 模糊决策
在得出Pareto 最优解集后,采用模糊决策方法选取最佳折中解,通常取标准化满意度最大的非劣解为最优折中解。一般隶属度函数表示为

式中:μr为第r个Pareto 最优解集中各非劣解的标准化满意度;l为在Pareto最优解的个数。
3 算例分析
3.1 算例陈述
为了验证本文提出调度模型的有效性以及算法的优越性,以某风电场和10台火电机组的电力系统进行仿真算例研究。设定一个调度周期T=24 h,绿色证书交易价格为20 美元/(MW·h),风电场发电成本价格为80 美元/(MW·h),风电惩罚成本为50美元/(MW·h),系统的正负旋转备用容量取系统负荷的5%,置信水平取0.95,可再生能源配额系数为0.15。碳交易价格为15 美元/t,碳排放权的裕度为0.4,碳交易的超额罚金价格为50 美元/t。MOEA/D-OLSMS 算法的参数设置见表1,火电机组发电成本及排污参数见表2 和表3,网损系数矩阵元素见表4,风电出力日预测曲线和日负荷预测数据如图1所示。

图1 负荷和风电出力预测曲线Fig.1 Load and wind power output prediction curves

表1 MOEA/D-OLSMS算法参数设置Tab.1 MOEA/D-OLSMS algorithm parameter settings

表2 机组能耗特性参数Tab.2 Energy consumption characteristic parameters of the units
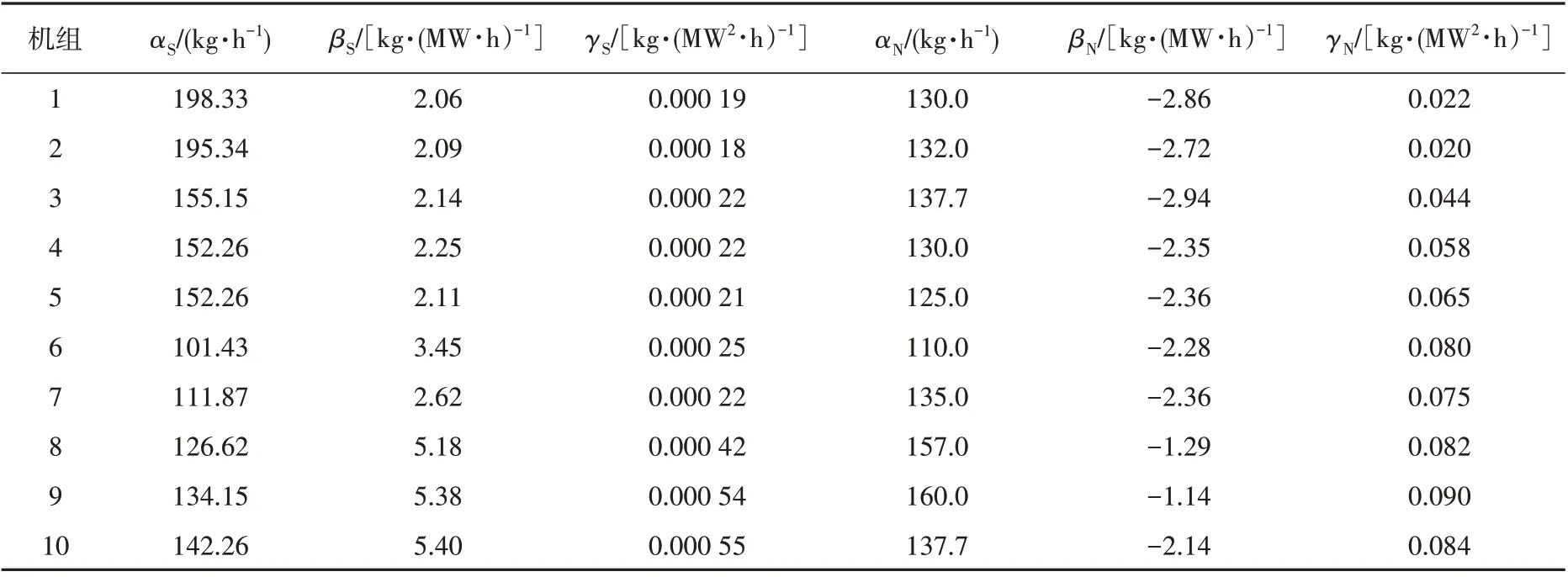
表3 机组排污特性方程参数Tab.3 Blowdown characteristic equation parameters of the units

表4 网损系数矩阵B元素Tab.4 Network loss factor matrix B element
3.2 仿真结果及分析
3.2.1 不同算法调度结果分析
为了验证本文所提MOEA/D-OLSMS 算法具有有效性和优越性,采用MOEA/D-OLSMS 和MOEA/D算法分别求解含风电电力系统环境经济调度模型。图2为算法求解模型得到的Pareto 最优边界,表5为2种算法求得的最优极端解和折中解。
由图2 可知,MOEA/D-OLSMS 算法求解的最优边界解要优于MOEA/D 算法,且本文算法求得的Pareto 最优解集在目标空间多样性要比MOEA/D 算法的范围更广,可为决策者提供更多更优的选择。
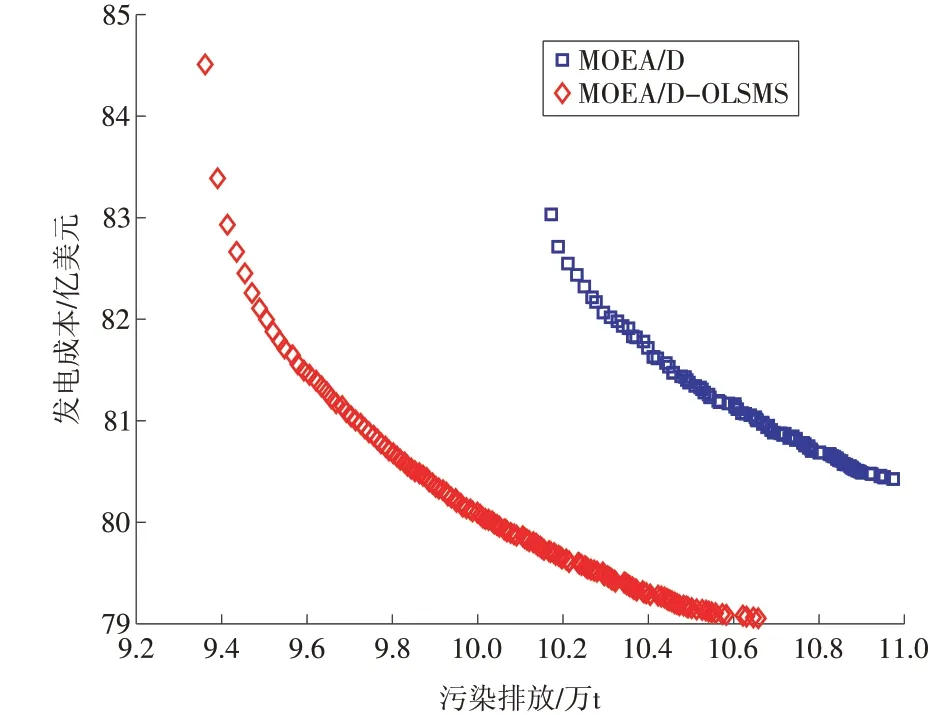
图2 不同算法下电力系统调度Pareto最优边界Fig.2 Pareto optimal boundary for power system dispatchingunder different algorithms
由表5 可知,在最优解方面,本文MOEA/DOLSMS 算法求得的经济成本和污染排放分别为79.60 万美元和93.61 t,相比MOEA/D 算法,经济成本减少了1.37 万美元,污染排放减少了5.12 t。在最优折中解方面,本文算法求得的最优折中解优于其他MOEA/D 算法,经济成本和污染排放分别为90.65 万美元和98.11 t。因此,本文所提MOEA/DOLSMS 算法在求解电力系统动态环境经济调度模型优于MOEA/D算法。

表5 不同算法的最优折中解和极端解Tab.5 Optimal compromise and extreme solutions of different algorithms
3.2.2 不同调度情景的结果分析
为了研究绿色证书交易机制和碳交易机制对含风电场电力系统环境经济调度的影响,设定3 种情景,见表6:情景1 为经济成本不计及绿色证书交易成本和碳交易机制;情景2 为经济成本只计及绿色证书交易成本;情景3 为经济成本同时计及绿色证书交易成本和碳交易成本。

表6 不同情景下的调度结果Tab.6 Scheduling results under different scenarios
通过调度结果可知,虽然情景2 较情景1 经济成本增加了7.05 万美元,但污染物排放量减少了0.82 t,同时风电惩罚成本减少了1.63万美元,说明风电出力增大,弃风量减少。考虑碳交易成本的情景3虽然经济成本较情景2上升了11.33万美元,但污染物排放量减少0.49 t,同时风电惩罚成本减少了0.38万美元,说明风电出力有所增大,弃风减少。由上可知,考虑绿色证书交易机制与考虑碳交易机制相比,在节能减排、促进风电出力、降低弃风率等方面的效果更佳。同时考虑碳交易成本和绿色证书交易成本的情景3 与情景1 相比,经济成本会进一步上升,但污染物排放量进一步减少,风电惩罚成本进一步减少。
在3 种情景下,10 台不同机组(G1—G10)的出力如图3 所示。G1 和G2 的出力最大,单位机组出力高,单位污染排放低。较于情景1,情景2 的部分机组出力有所减少,这是因为在负荷一定的情况下,风电机组出力增大导致火电机组出力减少。较情景1,情景3中G7和G10的机组出力有所增加,这是由于情景3 中计及了碳交易机制,同时情景3 中G7和G10的碳排放强度低于初始分配碳排放权。
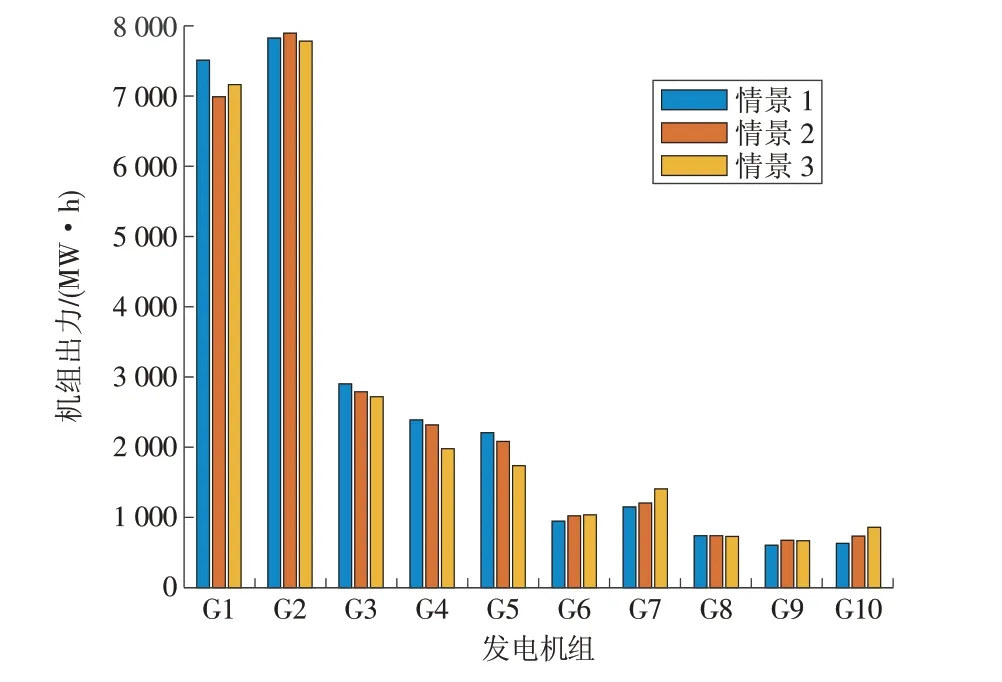
图3 不同情景下各火电机组出力对比Fig.3 Comparison of the output of each thermal power unit under different scenarios
图4 为某典型日3 种情景下的该风电场的风电出力。情景2 下的风电日消纳出力明显高于情景1的,情景3 下的风电出力又明显高于情景2 的,且情景1 的风电日消纳量为2 505 MW,与日前可调度风电最大出力相比,风电弃风量为443 MW,弃风率为15.01%。情景2的风电日消纳量2 768 MW,风电弃风量为180 MW,弃风率为6.11%,相较于情景1,弃风率降低了8.9%。情景3 的风电日消纳量为2 845 MW,与日前可调度风电最大出力相比,风电弃风量为103 MW,弃风率为3.47%。相较于情景2,弃风率降低了2.64%,相较于情景1,弃风率降低了11.54%。由此得出,计及绿色证书交易机制和碳交易机制对系统都具有促进风电消纳的作用,但计及绿色证书交易机制比计及碳交易机制的效果更佳。与此同时,同时考虑绿色证书交易机制和碳交易机制的在促进风电消纳,减少污染排放方面,效果会进一步提升。

图4 不同情景风电机组出力对比Fig.4 Comparison of wind turbine output under different scenarios
3.2.3 不同可再生能源配额系数的结果分析
为研究可再生能源配额系数(η)对系统成本及污染物排放量,以及风电出力的影响。设定3 种情景下不同的η分别为0.13,0.15,0.17。表7 为在不同可再生能源配额下系统的调度结果。
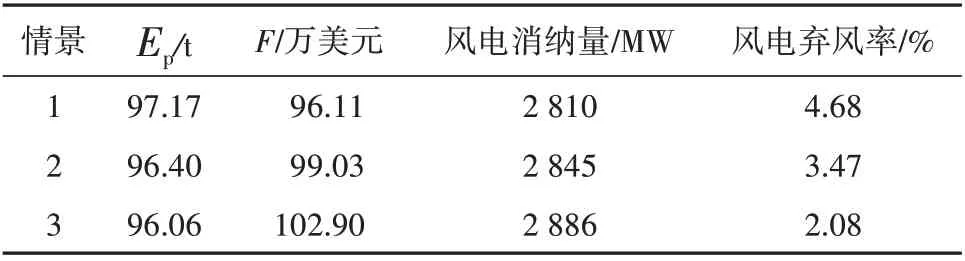
表7 不同配额系数下的调度结果Tab 7 Scheduling results under different quota coefficients
由表7可知,随着可再生能源配额比例的提高,虽然系统的经济成本增加,但污染物的排放量减少,同时风电日消纳量也会增加,风电弃风率也随之降低。这是因为系统必须完成规定的强制性配额任务,随着配额的提高,系统必须提高风电机组消纳量或者从绿色证书交易市场购买绿色证书数量。
4 结论
本文将碳交易机制和绿色证书交易机制同时引入电力系统中,构建一个计碳交易-绿证的含风电电力系统多目标动态环境经济调度模型,并提出一种基于反向学习混沌搜索多变异策略的MOEA/D-OLSMS算法对模型进行求解。
(1)本文所提MOEA/D-OLSMS 算法求解获得的最优边界和范围要优于MOEA/D 算法,证明了所提MOEA/D-OLSMS算法的有效性和优越性。
(2)本文将绿色证书交易机制、碳交易机制和风电惩罚机制引入电力系统中,在保证系统一定比例的绿色电能时,同时考虑火电机组的碳排放,有效提高了风电消纳能力,降低了系统污染物的排放量,提高了系统的环境效益,促进了可再生能源的发展。
(3)本文分析了可再生能源配额系数的不同对系统的影响。结果表明:可再生能源配额系数越高,系统中风电出力就越多或者购买更多的绿色证书数量,导致风电出力增加,风电弃风率降低,直接导致系统污染物排放量减少。
