义务教育阶段一个数学核心素养的评价框架

崔志翔，杨作东

义务教育阶段一个数学核心素养的评价框架

崔志翔1，杨作东2

（1．华东师范大学 教师教育学院，上海 200062；2．南京师范大学 教师教育学院，江苏 南京 210097）

数学核心素养是学生通过学科学习而逐步形成的正确价值观念、必备品格和关键能力．义务教育阶段数学核心素养的评价框架包括数学抽象、逻辑推理、模型思想、直观想象、数学运算、数据分析观念6个成分，针对这6个核心素养成分可以建立知识学习与技能掌握、数学思维与数学表达、问题解决与实践能力、数学情感4个评价维度．

数学核心素养；义务教育；核心素养评价

1 义务教育数学学科核心素养

1.1 核心素养的概念

作为数学课程深化改革的新导向，义务教育阶段数学核心素养的内容、评价标准和教材编制等层面的研究一直是数学教育研究的重点问题之一[1]．高中数学核心素养在《普通高中数学课程标准（实验）》（以下称《高中课标》）颁布后，许多学者已经对高中数学核心素养如何推广到义务教育阶段进行了探索性研究．李星云在PISA对数学素养的界定基础上，提出以数学交流为统领性的6个小学数学核心素养[2]；马云鹏指出数学核心素养是《义务教育数学课程标准（2011年版）》（以下称《义务教育课标》）中“四基”之数学基本思想在学习等领域内容中的具体表现，并具有综合性、阶段性和持久性的特征[3]；周淑红将小学数学核心素养划分为应用意识、运算能力、推理能力、几何直观4个成分，并建立了小学数学核心素养的生成和内容与表征模型[4]；熊丽给出了以“数学抽象”等6个成分为评价指标的数学第二学段数学核心素养评价指标体系，并将6个成分的具体内容划分作为了评价框架的二级指标[5]．纵观学者们对义务教育数学核心素养的探索性研究可以发现：不同学者对义务教育数学核心素养的成分划分不尽相同；针对义务教育数学核心素养的评价维度有不同观点；义务教育数学核心素养的评价框架研究欠缺．

1.2 义务教育数学核心素养成分

义务教育数学核心素养成分的确定是建立义务教育数学核心素养的评价框架的首要任务．而不同学者对义务教育数学核心素养成分划分的不尽相同，根源在于成分汲取的来源不同．近年来，将《高中课标》中对高中数学核心素养的6个成分的划分经过一定的修改后将其作为义务教育数学核心素养成分的做法，已成为一种趋势．其中，无论是曹培英基于教学实践基础提出了抽象、模型、推理、运算能力、空间观念、数据分析观念6个小学数学核心素养成分[6]，还是熊丽利用专家咨询法析出的数学抽象、推理能力、模型思想、运算能力、空间观念和数据分析观念的6个核心素养成分[5]，这些核心素养成分的划分都能够与《高中课标》中对高中数学核心素养的6个成分做到一一对应．然而，这种数学核心素养的划分方式是否能够真正既准确又全面地应用于义务教育的各个学段，仍然存在许多问题．（1）将《高中课标》中对高中数学核心素养的6个成分的划分直接移植成为、或经过一定修改后将其作为义务教育数学核心素养成分的做法是否合理，其是否能够满足对义务教育阶段学生数学核心素养培养的要求？（2）如若问题1的做法存在不合理情况，那么对于义务教育数学核心素养成分的确定，是应当在此基础上加入其它核心素养成分进行补充，还是对部分核心素养成分进行修改和替换，或者完全摒弃高中数学核心素养成分对义务教育数学核心素养成分划分的影响，提出新的义务教育数学核心素养成分的划分依据呢？

数学核心素养的本质是数学核心能力，核心素养培养的本质是对学生数学核心能力的要求[7]．在此基础上，想要解决上述问题，除了从其它关于数学核心素养成分的研究中寻找答案外，追本溯源地从以往的《义务教育数学课程标准》的内容中进行核心素养成分的探索，也许能够给出更好的参考答案．事实上，与《义务教育数学课程标准（实验稿）》相比，《义务教育课标》增加了在课程内容中应当对学生数感、数据分析观念等能力与意识培养的内容，这对义务教育数学核心素养成分的划分提供了重要的参考依据．基于这种研究视角，可将《高中课标》与《义务教育课标》为研究基础，定义出新的义务教育数学核心素养成分．

表1 《高中课标》核心素养与《义务教育课标》核心概念

通过对《高中课标》中的高中数学核心素养成分与《义务教育课标》中提出的10个核心概念进行对比分析可以看出，要将《高中课标》中对数学核心素养的6个成分的划分经过一定修改后，将其作为义务教育数学核心素养成分，则仍然需要解决另外两个问题．（1）《义务教育课标》数感、符号意识等未能与《高中课标》核心素养成分一一对应的核心概念是否能够融入到相对应的核心素养成分当中？（2）已确定的6个核心素养成分是否能够做到对核心概念中的应用意识和创新意识这些一般能力和品格的培养？

在《义务教育课标》中，数感被定义为学生关于数与数量、数量关系、运算结果估计等方面的感悟．曹培英基于数的现实意义以及数感在运算中的表现，结合了小学阶段运算教学的课时数和应用机会相对较大这一基本事实，将数感归属于运算能力[6]．需要厘清的是，数的概念的形成要在运算能力的形成之前产生，这种概念形成的本质是基于现实情境的抽象思维，这就是数感与数学抽象能力息息相关而非单纯归属于运算能力的重要依据之一．马云鹏认为数感是人们主动地、自觉地或自动化地理解数和运用数的态度与意识，数感的培养有利于学生有意识地将现实问题与数量关系建立起联系[8]．而徐文彬将数感的成分划分为“对数字关系和数字模式的意识”，以及运用这种对数字关系和数字模式的意识“灵活地解决数字问题的能力”两个部分[9]．史宁中指出：“学生数感的发展过程包括感悟多少、用数表示多少、建立数之间的关联、对数进行运算、形成数系概念等过程．”[10]基于学者们对数感能力的定义与成分划分，研究者认为数感的内涵包括：要求学生能够抽象出数与数量的概念，能够理解数量关系并具有运算、推理和分析的能力，以及掌握运用数量关系解决现实问题等多个维度．那么，对《义务教育课标》中数感的概念进行核心素养的划分后，可以发现实际上数感涉及到对学生数学抽象、数学运算、数据分析、逻辑推理、数学建模5个核心素养培养的部分内容．

《义务教育课标》中符号意识主要被分为能够理解与运用符号与数之间的知识内容，以及能够使用符号进行运算、推理、表达和思考．李艳琴认为掌握符号意识包括对数学符号的感受、体会、认识、理解和运用5个过程，具体表现是学生对数学符号进行信息加工和处理能力的反应[11]．数学符号意识可划分为对数学符号的表征、推理、运算、感知4个维度[12]，其基础是具备一定的数学符号能力，在数学对象与符号能力间建立敏感性反应，这是在学习和应用数学知识时运用数学符号进行表达、操作、思考的一种倾向[13]．培养学生对符号意识感受、理解与运用的本质是对学生数学抽象能力的要求，在此基础上，学生还需要达到能够运用数学符号进行数学运算与推理的高度．因此，可以发现符号意识是对学生数学抽象、数学运算、逻辑推理3个核心素养培养的部分内容．

对于应用意识和创新意识两个一般能力要求的核心概念，其本质是对学生基本能力而非数学能力的要求．不应被划入义务教育数学核心素养的成分，而是应当作为对学生核心素养水平划分的依据．学生的应用意识以及创新意识能够通过其对数学的学习、对数学核心素养的掌握来获得和提高，但这并非是获得和提高这两项意识的唯一途径．事实上，《高中课标》在课程目标的设置上，也要求学生通过发展数学核心素养，获得和提高“四基”与“四能”，并发展自身的创新意识、实践能力等一般素养．

另外，《义务教育课标》中的“数据分析观念”与“几何直观”“空间观念”3个核心内容与《高中课标》中“数据分析”与“直观想象”的核心素养成分的对比．尽管名称相似，但在实际内涵上仍有很大差别．义务教育阶段对于学生数据分析的能力要求处于起步阶段：更多的是让学生能够对数据分析有基本的了解和认识后，掌握最基本的数据分析观念，而非掌握运用数学方法对数据进行收集、处理、分析、推断的能力与素养．同样在“直观想象”层面，也并不要求义务教育阶段的学生掌握通过数形结合建立模型解决问题的思路与能力．

从而，将《高中课标》中的6个核心素养成分与《义务教育课标》中的10个核心成分进行补充和结合后，将“数学抽象”“逻辑推理”“模型思想”“直观想象”“数学运算”“数据分析观念”作为义务教育数学核心素养评价框架的核心素养成分使用，能够与《义务教育课标》中的8个数学核心概念相对应和补充．需要注意的是，部分数学核心素养成分的内涵在移植的过程中已经相应地进行了调整、扩充或缩减．以义务教育阶段的数学抽象核心素养为例，包括的内容已经扩充为从数与数量关系、数与符号关系、数量与数量关系、物体与图形关系等成分中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构并予以表征．在上述理论研究的基础上，同样可以对本节最初的两个问题给予回答：将《高中课标》中对高中数学核心素养的6个成分的划分需要经过一定修改后方可将其作为义务教育数学核心素养成分的划分，其能够满足课标对义务教育阶段学生数学核心素养培养的要求．但是，这些数学核心素养成分的深度、广度等在义务教育阶段具体已经发生了转变，其内容实质与高中数学核心素养的6个成分存在一定程度上的区别（如图1）．

2 义务教育数学核心素养的评价维度

由经济合作发展组织OECD举办的PISA不但开始关注学生在数学内容上的学习，而且极为重视数学过程的评价．PISA将学生核心素养的评价分为内容、过程和情境3个维度．部分学者也在此框架和基础上，编制了学生核心素养的测试题[5]．然而PISA的核心素养评价模型仍存在一些问题：它过多地强调学生解决实际问题的能力，过分追求数学问题的情境化．为了解决这个问题，喻平结合了PISA、彼格斯的SOLO模型以及布鲁姆的目标分类法，提出了将学生知识学习的3种形态（知识理解、知识迁移和知识创新）作为学生核心素养评价的3个维度[7]．但这种评价维度的本质是对学生数学能力的要求，没有考虑对学生品格等其它因素的发展需要．这仍然不能满足学界对于核心素养评价多元化的价值观念，也不能满足《义务教育课标》中评价方式多样化的要求．

除了已有的研究文献外，合理的评价维度的产生与落地必然需要与课程标准进行一定程度上的结合．事实上，将学生的数学学业评价与数学课程标准保持一致，也是数学教育评价研究中国内外研究者的主流做法．《义务教育课标》将学生数学学业学习评价分为了“知识技能”“数学思考”“问题解决”“情感态度”4个维度，尽管这4个维度是否能够适用于义务教育数学核心素养的评价有待商榷，但这对义务教育数学核心素养评价维度的确立具有重要的参考价值．

在PISA、喻平的知识学习理论以及《义务教育课标》中的学业水平划分维度的基础上，对义务教育数学核心素养的评价维度划分还要适当地考虑到当今数学教育研究的热点问题和内容，在理论与实际教学相结合的情境下做到对学生数学学习以及学生数学核心素养水平的多维评价．另外，问题解决、问题提出、数学能力、数学思考、数学文化等国内外数学教育研究最为关注的热点词汇[14–15]，也将成为义务教育数学核心素养评价维度的参考标准之一．从而可以将义务教育数学核心素养划分为4个维度：知识学习与技能掌握、数学思维与数学表达、问题解决与实践能力、数学文化与情感．

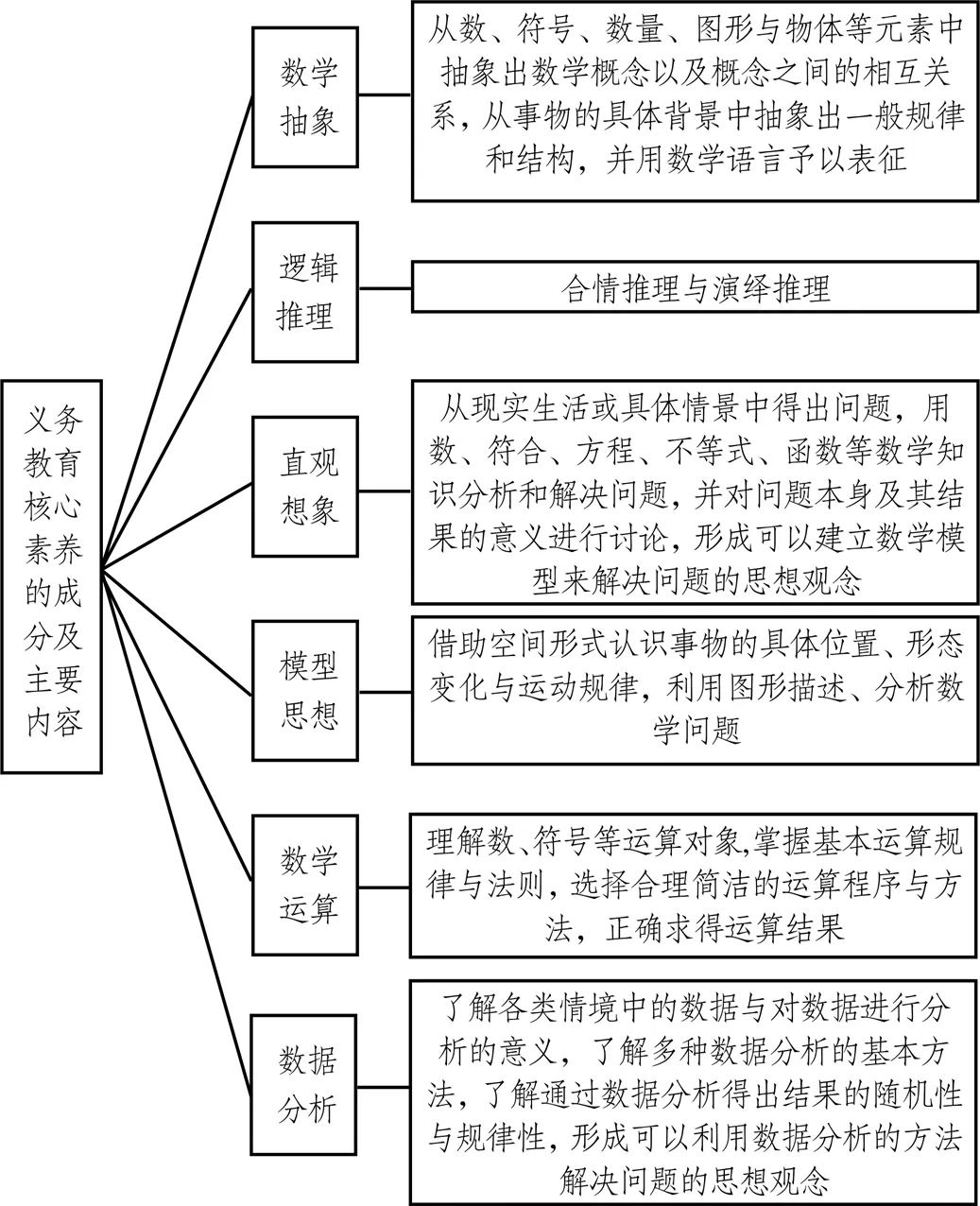
图1 义务教育核心素养的成分及其主要内容

2.1 知识学习与技能掌握

对学生数学知识与技能的要求是对学生学业水平评价的最基本要素．知识是指数学概念、法则、性质、公式、公理、定理以及由其内容所反映出来的数学思想和方法，技能是指能够按照一定的程序与步骤进行运算、作图或画图、进行简单的推理[16]．而对于“知识学习与技能掌握”维度的水平划分，则需要重新回到布鲁姆提出的知识观上去．按照定义，“知识学习与技能掌握”维度中的“知识”一词，指的是狭义的“知识”．而根据布鲁姆在《教育目标分类学:认知领域》的修订版中的知识观，广义的知识包含着陈述性知识和程序性知识，其中所定义的狭义的“知识”以及“技能”“思维”“算法”“策略”等概念皆在其中[17]．因此，对涉及这些概念的核心素养成分维度的水平划分，也完全可以参考喻平对高中数学核心素养成分的水平划分，即将其按照知识学习的3种水平：知识理解、知识迁移和知识创新来进行[7]．这样，“知识学习与技能掌握”维度，就可以划分为知识理解与技能形成、知识迁移与技能迁移、知识创新与技能突破．

2.2 数学思维与数学表达

学科思维的形成是培养学生核心素养的最高层次，它的本质是学科知识的创新[7]．而数学表达则是基于数学思维发展的基础上，用数学语言对数学知识的表述、评价、总结与拓展．对学生数学思维的培养包括两个概念：“使学生学会数学地思维”和“通过数学使学生学会思维”[18]，二者相辅相成．应当明确的是，学生数学思维的形成即为学生数学知识学习的过程，随着学生对知识学习水平的提高，学生的数学思维也在逐渐形成．它同样可分为3种水平：一是数学思路的产生，这是学生在数学学习的过程中，通过思考产生了对数学知识的感悟，体会到数学知识的意义、作用和思想；二是数学思想的产生，在这一阶段学生理解了不同知识间的逻辑关系，建立了网状的知识结构；三是数学思维的产生，学生开始具备“数学专家型直觉”，利用数学思维方式看待和处理问题，形成特定的世界观和方法论[7]．因此，“数学思维与数学表达”维度可以划分为：数学思路与简单表达、数学思想与逻辑表达、数学思维与思维表达．

2.3 问题解决与实践能力

问题解决与实践能力是侧重于学生数学学习的应用能力的考察维度，这种应用能力代表了知识学习的可操作性．需要指出的是，实践能力是问题解决在现实情境中的表现，而问题的难度差别则主要取决于问题所处的情境．问题情境的核心价值是其“思考性”[19]，这种对学生“思考性”的要求同样是学生知识学习的组成部分．因此，“问题解决与实践能力”维度的水平亦可分为3个阶段：第一，问题理解与实践能力发展，在熟悉的数学情境中解决简单的数学问题；第二，问题解决与实践能力获得，在新的或关联的数学情境中解决复杂问题；第三，问题与实践能力创新，在综合的数学情境中创新问题．

2.4 数学情感

培养学生的数学文化与数学情感对学生数学学习的重要性已经存在了大量理论与实证方面的研究[20–22]．但需解决的核心问题是：如何定义核心素养与数学文化、数学情感之间的关系．喻平认为核心素养成分的本质是能力，因此他对学生核心素养的评价框架中并没有考虑数学情感方面的因素[7]．但这种定义显然存在问题，对于学生核心素养的培养不可能忽略对学生必备品格方面的要求．蔡金法和徐斌艳认为数学情感应该是学生数学核心素养的组成成分[23]，但这种做法会使得“数学情感”的评价标准与其它核心素养成分的评价标准出现较大的差异，甚至可能要为其设置独立的评价维度．这容易导致“数学情感”与数学核心素养中其它成分的分离，也会使得教师在具体的教学过程中面临极大的挑战．

《高中课标》认为数学核心素养是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观．那么对数学核心素养的评价要求就不应局限于能力范围．为了满足核心素养对学生思维品质、情感、态度与价值观的评价要求，首先需要了解这4个成分的本质以及它们相互之间的关系．布鲁姆将教育目标分为认知、情感与动作技能3类，他认为学生的情感在教育中存在着一种逐渐形成的过程，这种过程包含5个层次：接受或注意、反应、价值评价、价值观的组织和品格形成．这就意味着思维品质、态度与价值观是教育情感目标的组成部分，他们代表的只是学生情感目标实现的不同程度[17]．因此完全可以单列一个情感维度去对学生基于数学核心素养的思维品质、情感、态度与价值观进行评价．事实上，在芬兰与德国的数学素养测评中，数学文化与数学情感也作为评价维度而非学科素养成分或能力存在[24–25]．学生数学核心素养的情感目标的培养需要教师能够带领学生挖掘数学知识的内在价值，做到“深度教学”[26]．这种超越表层的知识符号学习的教学方式，能够做到真正培养学生的能力与情感．而在这种“深度教学”当中，学生数学核心素养情感目标的生成存在两种路径，一是由数学核心素养成分本身引出数学情感：例如学生对数学建模本身引起注意、产生兴趣，进而对其价值观与品质产生影响；二是由数学核心素养成分相关联的哲学、艺术、历史、教育、思维科学、环境等数学文化作为载体，促进学生的数学情感的生成与发展[27]：例如学生在图形知识的学习中感受到了数学美，进而对其产生好奇心，因此促进了学生直观想象素养的情感发展．由于这种基于数学文化的影响是非常复杂的，因此将数学文化与情感维度的水平划分着力于“情感”层面，即“数学情感”维度：分别为情感的接受或注意、情感反应、情感的价值评价、价值观的组织和品格的形成5个阶段．

3 义务教育数学核心素养的评价框架

3.1 一个评价框架

在确定了义务教育阶段的核心素养成分及其评价维度后，就可以直接得到义务教育数学核心素养评价的理论框架（如表2）．该理论框架以基本的教育学理论为说理，具备针对性以及多元的评价标准，能够满足对于义务教育阶段学生数学学习核心素养评价的整体性要求；能够为学生的数学核心素养水平的测量以及教师在设计针对学生核心素养发展的教学过程中提供实质性的帮助．

需要注意的是，对于不同的知识点与知识模块，能够体现的数学核心素养成分都是不同的，在能够匹配的评价维度以及相匹配各维度的对应水平划分上也存在差异[28–31]．这需要使用者在实际的教学以及对学生的测量当中根据实际情况进行选择和变化．

表2 义务教育数学核心素养的一个评价框架

3.2 具体操作示例

接下来结合义务教育第二学段中“圆的面积”章节的内容给出更具体的实例说明：

作为小学阶段数学学习的难点之一，“圆的面积”章节相关的核心素养成分相对较多，包含了数学抽象、逻辑推理、模型思想、直观想象、数学运算5个核心素养成分．下面对学生通过该知识点学习后，各个核心素养成分达到的水平进行举例说明（如表3）．

需要指出的是，在使用该评价框架对学生的核心素养进行具体评价时，教师作为评价者除了应当保证对知识点的各个核心素养成分的评价全面性、不遗漏或偏重于某些成分的测量外，还应对学生采用多元化的评价手段来保证对其各水平维度的评价准确性．例如在该章节的知识学习与技能掌握评价维度上，教师应当对试题的编纂保持一定的开放性，考察学生在圆的面积公式内容创新能力，引导学生对圆的面积公式采用多种方式进行推导、归纳和总结．而在数学思维与数学表达评价维度层面，应当尽可能地创设多种情境对学生的思维能力和表达能力进行考察，如应当将学生在现实情境中的数学口语表达情况纳入评价范围．在问题解决与实践能力维度上，可以尽量模拟真实环境，考察学生在现实情境中结合已学习的内容寻找问题、提出解决方案、实际解决问题的能力和创新能力：如让学生观察生活中常见的各类井盖并测量其面积，思考为何不同类型和用处的井盖规格不一，探索为什么要将其设置成不同形状的原因，以及有没有更好的形状和类型可以替代现有井盖的标准；再结合其在各个层面的表现情况进行评价．而在数学情感维度的评价上则更需要教师等评价者对学生个体进行长期、深入的观察与互动，最终的评价结果也应当在与学生个体、学生家长、学生同伴等群体进行交流后综合评判给出．

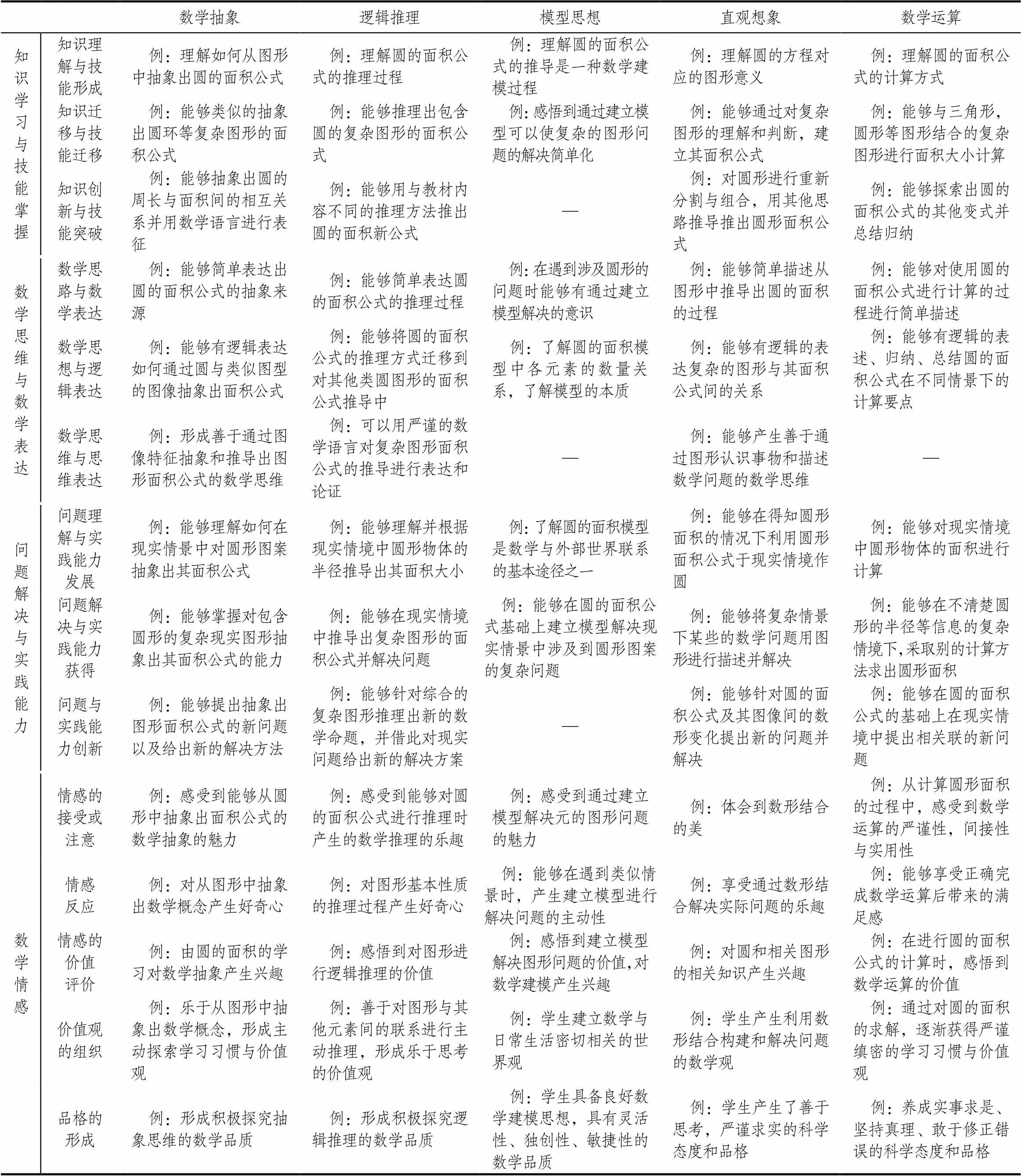
表3 “圆的面积”章节学生核心素养水平维度示例

研究者旨在对参与者的解题情绪过程进行深入、细致、整全的解释性诠释，不在量化意义上进行推广．研究的相关发现和结论可为量化研究提供借鉴．若把多种情绪因素放在一起综合分析，不难发现，影响个体数学问题解决的原因可能大相径庭，个体之间存在明显的差异，但有一点是共同的，即情绪因素显著地影响着学生的数学问题解决．之所以如此，其核心在于，认知与情绪均是整体心理机制的组成部分，二者融为一体，在问题解决中相互影响、密不可分[10]．因此，情绪、动机、效能感等情感因素会积极参与到学生的数学问题解决过程之中，同时又扮演着认知处理的风向标、阻碍物以及助推器的角色．

[1] 杜宵丰，周达，刘坚．义务教育数学课程沿革：核心素养的视角——以问题解决为例[J]．教育理论与实践，2018，38（17）：10–13．

[2] 李星云．论小学数学核心素养的构建——基于PISA2012的视角[J]．课程·教材·教法，2016，36（5）：72–78．

[3] 马云鹏．关于数学核心素养的几个问题[J]．课程·教材·教法，2015，35（9）：36–39．

[4] 周淑红，王玉文．小学数学核心素养的特质与建构[J]．数学教育学报，2017，26（3）：57–61．

[5] 熊丽．小学第二学段学生数学核心素养评价指标体系构建研究[D]．重庆：西南大学，2017：1．

[6] 曹培英．小学数学学科核心素养及其培育的基本路径[J]．课程·教材·教法，2017，37（2）：74–79．

[7] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19–23，59．

[8] 马云鹏，史炳星．认识数感与发展数感[J]．数学教育学报，2002，11（2）：46–49．

[9] 徐文彬，喻平．“数感”及其形成与发展[J]．数学教育学报，2007，16（2）：8–11．

[10] 史宁中，吕世虎．对数感及其教学的思考[J]．数学教育学报，2006，15（2）：9–11．

[11] 李艳琴，宋乃庆．小学低段数学符号意识的含义及其表现形式[J]．课程·教材·教法，2016，36（3）：92–97．

[12] 朱立明，马云鹏．“数学符号意识”研究：内涵与维度[J]．教育理论与实践，2015，35（32）：6–8．

[13] 张号，童莉，黄翔．数学符号 从“感”到“意识”[J]．数学教育学报，2014，23（1）：100–102．

[14] 任子朝，孔凡哲．数学教育评价新论[M]．北京：北京师范大学出版社，2010：10–14．

[15] 徐柱柱，綦春霞．近二十年（1999—2018）来国外数学教育研究进展——基于WOS数据库3061篇SSCI文献的共词分析[J]．外国中小学教育，2018（6）：72–80，46．

[16] 王红蔚．中小学数学课程标准与教材研究[M]．郑州：郑州大学出版社，2017：42–43．

[17] 魏宏聚．新课程三维目标表述方式商榷——依据布鲁姆目标分类学的概念分析[J]．教育科学研究，2010（4）：10–12，16．

[18] 郑毓信．“数学与思维”之深思[J]．数学教育学报，2015，24（1）：1–5．

[19] 任旭，夏小刚．问题情境的创设：基于思维发展的理解[J]．数学教育学报，2017，26（4）：15–18．

[20] 付天贵，宋乃庆．数学文化及其在小学素质教育中的价值[J]．教育研究与实验，2018（6）：58–63．

[21] 王娟．数学学习的情感、自信、价值与成就之关系——由TIMSS 2007的结果分析亚洲五国（地区）[J]．外国中小学教育，2009（10）：46–49．

[22]  CAI J, MERLINO F J. Metaphhor: A powerful means for assessing students’ mathematical disposition [C] // BRAHIER D J, SPEER W. Motivation and disposition: Pathways to learning mathematics——NCTM 2011 yearbook. Reston: NCTM, 2011: 147–157

[23] 蔡金法，徐斌艳．也论数学核心素养及其构建[J]．全球教育展望，2016，45（11）：3–12．

[24]  HENDRICKSON K A. Learning from Finland: Formative assessment [J]. The Mathematics Teacher, 2012，105 (7): 488–489.

[25]  WEINERT F E. Lerstungsmessung in schuim [M]. Weinheim Und Basel: Beltz, 2003:17–23.

[26] 姚林群，郭元祥．新课程三维目标与深度教学——兼谈学生情感态度与价值观的培养[J]．课程·教材·教法，2011，31（5）：12–17．

[27] 黄秦安．数学文化观念下的数学素质教育[J]．数学教育学报，2001，10（3）：12–17．

[28] 史宁中，吕世虎，李淑文．改革开放四十年来中国中学数学课程发展的历程及特点分析[J]．数学教育学报，2021，30（1）：1-11．

[29] 张玉环，周侠，陈爽．核心素养视角下中法高考数学试题的比较研究——基于2015—2020年中国和法国高考数学试卷[J]．数学教育学报，2021，30（1）：42-48．

[30] 赵思林，潘超．中学数学教师核心素养及构成要素[J]．数学教育学报，2021，30（2）：48-54．

[31] 路江江，王亚妮．高中数学教育中如何培养学生的数学核心素养——王尚志教授访谈录[J]．数学教育学报，2021，30（2）：67-70．

An Evaluation Framework of Mathematics Key Competencies in Compulsory Education

CUI Zhi-xiang1, YANG Zuo-dong2

(1. School of Teacher Education, East China Normal University, Shanghai 200062, China;2.School of Teacher Education, Nanjing Normal University, Jiangsu Nanjing 210097, China)

The key competencies of mathematics are the correct values, essential character, and key abilities that students develop gradually through subject study. The evaluation framework of mathematics key competencies in compulsory education consists of six components: mathematical abstraction, logical reasoning, model thinking, intuitive imagination, mathematical operation, and the concept of data analysis. According to these six key competencies of mathematics, four evaluation dimensions can be established: knowledge learning and skill mastery, mathematical thinking and expression, problem solving and practical ability, and mathematical emotion.

key competencies of mathematics; compulsory education; evaluation of key competencies

G632.4

A

1004–9894（2021）05–0047–06

崔志翔，杨作东．义务教育阶段一个数学核心素养的评价框架[J]．数学教育学报，2021，30（5）：47-52．

2021–06–14

教育部学校规划建设发展中心重大课题——基于“博雅云课堂”的“双螺旋交互”智慧学习模型的研究（CSDP18FS1101）

崔志翔（1995—），男，安徽滁州人，博士生，主要从事数学课程与教学论研究．

[责任编校：陈汉君、陈隽]