习题变式巧遇中考试题 素养渗透妙转通性解法*——基于三条切线几何综合题的解法及变式思考

广东省中山市小榄镇旭日初级中学(528415) 何 勇

1 习题变式

习题变式是指通过改变题目非本质的特征,引导学生从变中发现不变,从不变的数学本质中探究变的规律.学生在习题变式中经历不同条件、不同结论、不同图形、不同角度、不同思路却同一数学本质的过程,感知分析问题、体验解决问题的乐趣,从而使数学知识结构更立体化.更能使不同的人在数学上得到不同的发展.主要形式包括:

一题多思变式.同一题目从不同角度思考问题,探究不同的解答方法,学生拓宽思路、发散思维,也就是常见的一题多解.

多题归一变式.将解决一个问题的方法加以归纳总结、形成通性技巧,特殊结论一般化,并用于解决某一类题目,学生迁移知识、提炼运用,达到多题归一的目的.

多题多变变式.从一个题目或多个题目出发,变化条件、变化结论、变化图形、变化符号、变化情境、变化形式、变化维度,学生探究新知、综合分析、完善知识,达到循序渐进、举一反三、触类傍通的目的.

2 教材习题

例1如图1,⊙O的直径AB=12cm,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于点D,C两点.设AD=x,BC=y,求y关于x的函数解析式,并试着画出它的图像.(此题是2014年人教版数学九年级上册第125 页第15 题.篇幅有限,本文不研究图像的画法.)

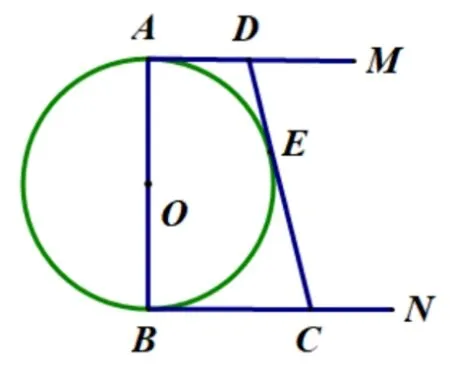
图1

这是一个关于三条切线的几何综合题,利用切线的性质,可知图中AM和BN互相平行,且都垂直于直径AB.

思路 1: 作辅助线DF⊥BN,利用勾股定理就可以得到y关于x的函数解析式.

解法如图2,过点D作DF⊥BN,∵AM,BN是⊙O的切线,∴∠A= ∠B= ∠BFD= 90°,∴四边形ABFD是矩形,∵AB= 12cm,AD=x,BC=y,∴DF=AB=12cm,BF=AD=x,∴CF=BC −BF=y −x,

图2

∵AM,BN,CD是⊙O的切线,A,B,E是切点,∴由切线长定理,DE=DA=x,CE=CB=y,∴DC=DE+EC=x+y,∵在RtΔDFC中DC2=DF2+FC2,∴(x+y)2=122+(y −x)2,整理得xy=36,∴y=

思路2作辅助线,连接OD,OE,OC,构造全等三角形和相似三角形,利用熟悉的射影型相似三角形对应边成比例的性质就可以得到y关于x的函数解析式.

解法2如图3,连接OD,OE,OC,∵AM,BN,CD是⊙O的 切 线,A,B,E是 切 点,∴ 由 切 线 长 定理DE=DA=x,CE=CB=y且OE⊥CD,∠A= ∠B= 90°,∴在RtΔDOA和RtΔDOE中

图3

∴RtΔDOA∽= RtΔDOE(HL),∴∠1 =∠2 =同理得RtΔCOB∽= RtΔCOE,∴∠3 =∠4 =∴∠2 + ∠3 =(∠AOE+∠BOE)=90°,∵OE⊥CD,∴∠5+∠3=90°,∴∠2 = ∠5,又∵∠OED= ∠CEO= 90°,∴ΔOED∽ΔCEO,∴即DE · CE=OE2,∵直 径AB= 12cm,∴半 径OE= 6cm,∴xy= 62= 36,即y=

思路3作辅助线,连接OD,OE,OC,构造全等三角形和相似三角形,利用熟悉的K 字型相似三角形对应边成比例的性质就可以得到y关于x的函数解析式.

解法3同解法2 得∠2+∠3=90°,∴∠1+∠4=90°,∵∠A= ∠B= 90°,∴∠6 + ∠4 = 90°,∴∠1 = ∠6,∴ΔOAD∽ΔCBO,∴即AD·CB=OA·BO,∵直径AB= 12cm,∴半径OA=OB= 6cm,∴xy=6×6=36,即y=

设计意图与思考: 通过三种解题思路,学生经历从不同角度分析、解决问题的过程,体验多维模式、拓宽思路、发散思维、积极创新,掌握分析解决问题的多样基本思想方法.在研究图形性质、借助图形思考问题的过程,初步建立几何直观,发展数学核心素养.

通过上述思路解法我们发现,y关于x的函数解析式与⊙O的半径有关,并且此题只给出了直径AB= 12cm 的数据,不妨改变⊙O的直径这一数据,其他题干条件不变来探究三条切线交点的切线长AD,BC与半径之间的函数解析式.

变式1如图1,AM和BN是⊙O的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于点D,C两点.试探究AD,BC与⊙O半径r之间的关系?

分析模仿例1,设AD=x,BC=y,半径AB= 2r,则半径OA=OB=OE=r.

根据例1 的思路1,在RtΔDFC中DC2=DF2+FC2,有(x+y)2= (2r)2+ (y −x)2整理得xy=r2,即AD·BC=r2.

根据例1 的思路2,ΔOED∽ΔCEO,有即DE·CE=OE2,∵半径OE=r,由切线长定理DE=DA=x,CE=CB=y,∴xy=r2即AD·BC=r2.

根据例1 的思路3,ΔOAD∽ΔCBO,有即AD ·CB=OA · BO,∵半径OA=OB=r,AD=x,CB=y,∴xy=r2,即AD·BC=r2.

设计意图与思考: 通过直径特殊值到一般化,得到基于圆中三条切线交点的切线长AD,BC与半径之间的通用函数解析式为:AD·BC=r2.把这一题目推广到一类题目,学生体会通过推理探索数学结论,培养知识方法的迁移视野,提升合情推理和演绎推理的能力,形成解题的通性解法,增强学习数学的兴趣,初步形成总结归纳意识,发展数学核心素养.

3 试题呈现

例2如图4,在四边形ABCD中,AD//BC,∠DAB=90°,AB是⊙O的直径,(此题是2020年广东省中考22 题.篇幅有限,本文只研究第2 问的解法.)

图4

(1)求证: 直线CD与⊙O相切;

(2)如图5,记(1)中的切点为∠BCD.求tan ∠APE的值.

图5

分析此题是教材习题的变式运用,据例1 三种思路可知,本题求解方法多样.由上述例1 变式的三种思路得结论AD ·BC=r2,都可先求出r2=AD ·BC= 1×2 = 2,得OA=r=如图6,在⊙O中,由得,据RtΔDOA∽= RtΔDOE得∠1 = ∠2 =即∠APE= ∠1,又因为在RtΔAOD中,tan ∠1 =所以tan ∠APE=

图6

4 核心素养视角的解读

4.1 源于教材、习题铺垫

例2 这一道中考试题是三条切线几何综合题的变式运用,来源于教材、习题作铺垫.以几何综合知识为主,情境熟悉、题干简洁、图形直观、知识丰富、选择多样、重点突出,通过变式探索不同问题中的数量关系和变化规律,附带考查学生的代数运算能力,覆盖的知识点有切线的判定定理、切线的性质定理、勾股定理、全等三角形的判定与性质、相似三角形的判定与性质、圆周角定理及推论、同角(等角)的余角相等、锐角三角函数、最简二次根式等.

学生在熟悉的题干以及图形变式过程中感知、分析、研究,将自己所学的数学知识按照数学的内在逻辑和解题所需要的线索组成突破问题的结构链,通过直观想象演绎推理,培养化归思想,发展数学核心素养.

4.2 几何直观、解法明朗

学生通过一题多解可以增强学习数学的兴趣,知识结构日趋完善,经历借助图形思考问题的过程,初步建立几何直观.

从三条切线的熟悉图形中,综合分析,提炼出半径与三切线交点的切线长之间的关系.无论是从勾股定理,还是相似三角形入手都考查了学生的建模思想、几何直观想象、数据分析能力,借助几何直观来分析数量关系,把问题与常见的几何图形巧妙结合,充分感知教材习题到中考试题的变与不变.学生从题目的已知条件、从教材所学知识出发充分体验、主动发现和建构,根据题目线索,逐渐形成解题思路,将解题策略进行归纳整理.

此题关注学生差异,搭建解题视角的多维性和解题方法的多样性,充分发挥学生思维的独立性、广阔性、创新性,紧扣课标、拓展广度、调节深度,充分体现不同的人在数学上有不同的发展这一课程理念.

提炼出简化的熟悉图形如下:

图7

5 “8 字型”习题变式的思考

选择一些典型的习题作为素材,进行变式训练,挖掘题目通性解法,提炼解题模型,有助于学生丰富数学知识、提高解题能力、领悟思想方法、强化直观想象、发展数学素养.

5.1 基础练习: 以三角形全等的判定为例

例3 如图8,AC和BD相交于点O,OA=OC,OB=OD,求证AB//DC.

图8

变式1如图9,点C,F,E,B在同一条直线上,∠1 =∠2,CE=BF,DF=AE,写出AB与CD之间的关系,并证明.

图9

变式2如图10,点B,F,E,C在同一条直线上,CE=BF,AB//CD,AE//DF,求证AB=CD.

图10

变式3如图11,点B,F,E,C在同一条直线上,AE=DF,AB//CD,AE//DF,求证BF=CE.

图11

变式4如图12,点C,F,E,B在同一条直线上,AB=CD,AE=DF,CE=BF,求证AF//DE.

图12

变式5如图13,点C,F,E,B在同一条直线上,AB=CD,AE⊥BC,CE⊥BF,求AC与BD之间的关系,并证明.

图13

设计意图与思考: 从学生熟悉的8 字型图形着手,分别演变图形、改变形式、改变条件、改变问题对象等进行习题变式,内容精简、形式多样,由浅入深演变,符合绝大多数学生的认知能力和认知水平.涉及三角形全等的五个判定,覆盖全面、知识系统,学生掌握基本的证明方法,从中感知习题变式、知识立体化,体验分析、推理过程,在研究图形变换、习题变式过程中,进一步发展几何直观,在运用数学表达和解决问题的过程中,学生能积极参与,对几何有强烈的好奇心和求知欲,感受成功的快乐.

5.2 拓展探究: 以三角形内角和的应用为例

例4如图14,直线AC和BD相交于点O,试探究∠A+∠B与∠C+∠D的数量关系.

图14

变式如图15,直线AC和BD相交于点O,∠DCO和∠ABO的平分线相交于点P,试探究∠P与∠A,∠D的数量关系.

图15

8 字型基本图形中除了一对对顶角相等外,我们容易得出一个三角形中两个角的和等于另一个三角形中两个角的和,即图14 中∠A+ ∠B= ∠C+ ∠D.在例4 的变式中,在8 字型的基础上引入两条角平分线就形成变式,学生依照认知特点,循序渐进,需准确识别出与问题相关的8 字型.问∠P与∠A,∠D的关系,应选取∠P与∠A在同一个8 字型中,∠P与∠D在同一个8 字型中,这是解决本题的关键点.在本题中,由CP,BP 是角平分线得∠1 = ∠2,∠3 = ∠4,据图16 提炼出来的两个8 字型可知:∠D+∠1=∠P +∠3,∠A+∠4=∠P +∠2,两个式子相加后,化简即可得∠A+∠D =2∠P.

图16

设计意图与思考: 基本图形及其变式为图形识别的学习,建立初步几何直观提供了合适的机会.通过基本图形演变,合理铺垫,搭建梯子,减缓解决问题的思维坡度.学生体会通过合情推理探索数学结论,运用演绎推理加以证明的过程,锻炼看图分析能力,发展合情推理与演绎推理的能力,体会数学的基本思想和思维方式.

6 教学反思

教无定法,贵在得法.题目永远做不尽,所谓题海战术容易使学生疲倦,“一题多思、多题归一、多题多变”的变式训练,凸显题干本质及图形特点,以学生为主体,开拓分析思路,扩展解题视角,活跃学习思维.

课堂教学上进行习题变式,要由浅入深、循序渐进,启发学生主动探究、寻找关键信息、提取题干本质、识别熟知图形.鼓励学生以原题出发,通过变式优化知识结构,螺旋上升理解掌握一系列数学知识;以点带面分析解决一连串数学问题;多题归一提炼生成一篮子通性解法.鼓励学生模仿表达创新变式,提升感官认识,严谨推理逻辑,激发学习兴趣,延伸课程应用,内化渗透基本图形中重要的思想方法,领悟万变不离其宗的数学本质,发展数学核心素养.